三种不同类型BP网络及分析
一、mnist1.py分析
minist1.py是一个一层的神经网络。
1.1 对循环轮数进行分析
| 轮数 | 在测试集的准确率 |
|---|---|
| 1 | 0.0648 |
| 40 | 0.1361 |
| 360 | 0.2215 |
| 720 | 0.2936 |
| 1024 | 0.3538 |
| 1600 | 0.4604 |
| 2000 | 0.5251 |
| 2400 | 0.5787 |
| 2800 | 0.6226 |
| 3200 | 0.6561 |
| 3600 | 0.6848 |
| 4000 | 0.7068 |
绘制图形 得出一个分析结论
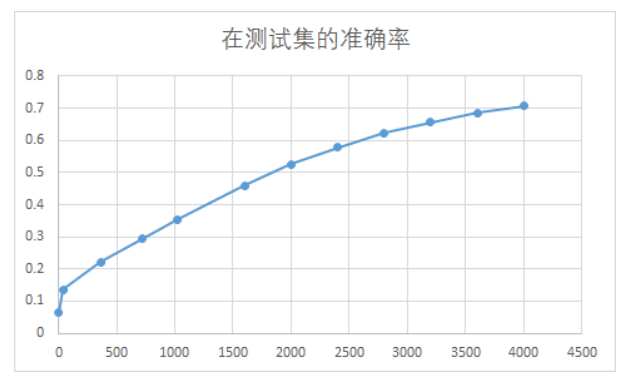
可以看到 在测试集的准确率随着训练轮数的增加而增加,并且随着训练轮数的增加,增加的幅度在减弱。
进一步分析 在程序中记录每轮后在测试集上的分数 用matplotlib绘制轮数与正确率的关系图 。
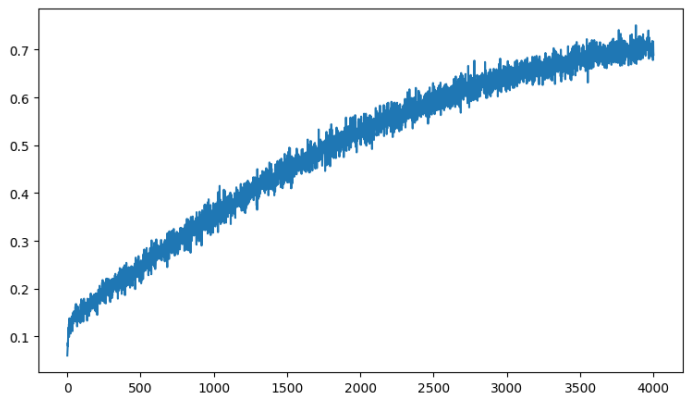
可以看出虽然在局部随着训练轮数的增加,正确率有起伏,但整体的趋势是增加的,并且增加趋势与上图一致。
在搭建模型的过程中,一开始循环轮数设为40,正确率只有0.13,后来用一个比较大的数4000作为循环轮数后,模型得到了明显改善,争取率达到0.7068,并且根据上图可以大胆预测,将循环轮数设为更大的数如10000或15000,正确率还能提高!
1.2 改变学习率
尝试不同学习率对模型的影响(循环轮数设置为4000)
| 学习率 | 在测试集的准确率 |
|---|---|
| 0.5 | nan |
| 0.1 | 0.8539 |
| 0.01 | 0.7068 |
| 0.001 | 0.2297 |
一开始使用的学习率为0.01 在循环4000轮后正确率为0.7068 然而当学习率提升为0.1时,正确率提升至0.85 结合上面的分析,当循环轮数增加时,正确率呈上升趋势 这也表明当前的学习率略低,模型始终在拟合,还远未到最优解附近,因而提升学习率之后,正确率得到了提升。
然而,当我把学习率改为0.5时,loss值不收敛了,这由于学习率设置的过大,越过最低点,无法达到最低点。
当学习率改为0.001时,争取率只有0.2297,是由于学习率太慢,经过4000轮迭代仍然远远未达到最优解附近。
1.3 改变损失函数
观察不同损失函数对于模型的影响(学习率0.1)
| 损失函数 | 循环轮数 | 在测试集的准确率 |
|---|---|---|
| 均方误差 | 4000 | 0.8539 |
| 交叉熵 | 200 | 0.88 |
| 交叉熵 | 400 | 0.894 |
| 交叉熵 | 600 | 0.886 |
| 交叉熵 | 800 | 0.926 |
| 交叉熵 | 1000 | 0.935 |
| 交叉熵 | 1200 | 0.931 |
| 交叉熵 | 1400 | 0.932 |
对比可得,当使用交叉熵时,只需迭代200轮,在测试集的准确率就超过了使用均方误差时循环4000轮的准确率。这表明,交叉熵时比均方误差更适用的损失函数。
1.4 改变随机种子
改变对权的初始化,观察对模型影响(循环4000轮,学习率0.1,梯度下降优化器)
| 随机种子 | 在测试集的准确率 |
|---|---|
| 42 | 0.7065 |
| 1 | 0.7118 |
| 12345 | 0.7225 |
随机种子的选择会影响权值的初始化,进而影响模型。但是分别选择比较小的随机种子1和比较大种子12345,对模型的影响差别并不大。
二、mnist2.py分析
mnist2.py构建了一个三层的BP网络,使用了正则化优化技术,使用Adma优化器。
2.1 改变节点个数
| 第一层节点数 | 第二层节点数 | 第三层节点数 | 在测试集上的准确率 |
|---|---|---|---|
| 1000 | 200 | 10 | 0.9621 |
| 5000 | 2000 | 10 | 0.9546 |
| 30 | 20 | 10 | 0.9452 |
| 100000000 | 20 | 10 | 无法运行 |
| 1000000 | 20 | 10 | 无法运行 |
| 100000 | 20 | 10 | 无法运行 |
| 10000 | 20 | 10 | 0.2567 |
- 尝试使用大的中间层节点数,5000和2000;尝试使用很小的中间层节点数 30和20;均未对准确率产生比较大的变化,但是中间层节点数大的时候,程序运行需要更久的时间
- 尝试第一层节点数特别大(一亿),第二层的很小,程序无法运行
- 尝试第一层节点数特别大(一百万),第二层的很小,程序无法运行
- 尝试第一层节点数特别大(十万),第二层的很小,程序无法运行
- 尝试第一层节点数特别大(一万),第二层的很小时程序运行结果准确率只有0.2567;说明提高隐藏层的节点个数并不能确定的提高准确率
2.2 改变学习率(节点个数1000和200)
| 学习率 | 在测试集的准确率 |
|---|---|
| 0.5 | 0.1135 |
| 0.1 | 0.1028 |
| 0.01 | 0.9621 |
| 0.001 | 0.2375 |
表明学习率设置过大或者过小都不能提高正确率
2.3 选择不同优化器(节点个数1000和200)
| 优化器 | 在测试集的准确率 |
|---|---|
| 梯度下降 | 0.8093 |
| Adam | 0.9621 |
| Momentum 冲量(0.9) | 0.878 |
| Momentum 冲量(0.5) | 0.6487 |
| Momentum 冲量(0.1) | 0.8148 |
| Momentum 冲量(0.001) | 0.7849 |
在本网络中,Adam优化器表现最好。
2.4 更改激活函数
| 激活函数 | 在测试集的准确率 |
|---|---|
| relu | 0.9621 |
| sigmod | 0.8384 |
| swish | 0.9381 |
| tanh | 0.9417 |
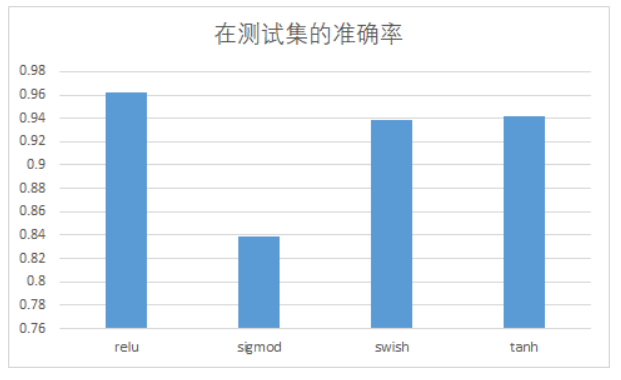
更换不同的激活函数对正确率有影响,其中最优的还是relu
三、mnist3.py分析
mnist3.py构建了一个五层的BP网络,使用了可变的学习率来优化网络,使用sigmod激活器,使用Momentum优化器
3.1 最初学习率对模型影响
| 最初学习率 | 在测试集的准确率 |
|---|---|
| 0.01 | 0.4272 |
| 0.1 | 0.7359 |
| 0.9 | 0.1135 |
| 0.0001 | 0.0859 |
搭建网络时一开始并没有用可变衰减率,后来加上可变学习率,初始学习率设为0.01,结果准确率在百分之40,后来改为0.1,正确率达到百分之70。
- 尝试使用很大的最初学习率---0.9
- 尝试使用很小的最初学习率---0.0001
最初学习率选择不能过大也不能过小,过大则会 使开始时学习步幅多大,无法达到最优点,最初学习率过小则会导致学习速度过慢。
3.2 改变激活函数
| 激活函数 | 在测试集的准确率 |
|---|---|
| relu | 0.098 |
| sigmod | 0.7359 |
| swish | 0.098 |
| tanh | 0.1135 |
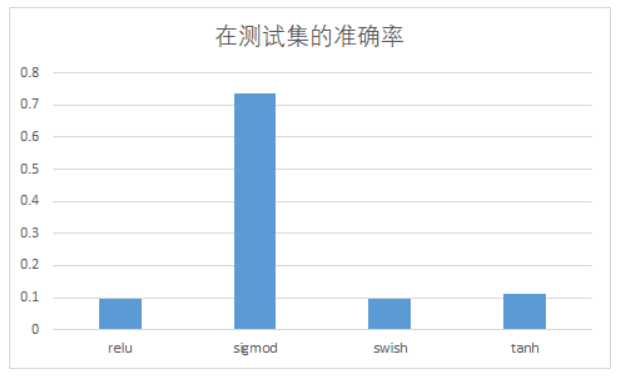
一开始使用的是sigmod激活函数,准确率0.7359,改用激活函数后,准确率都下降的非常低;通过观察最后的w1和b1发现,最后很多w1和b1都是nan。
3.3 改变优化器
| 优化器 | 在测试集的准确率 |
|---|---|
| 梯度下降 | 0.4343 |
| Adam | 0.1135 |
| Momentum 冲量(0.9) | 0.7359 |
| Momentum 冲量(0.5) | 0.5251 |
| Momentum 冲量(0.1) | 0.457 |
| Momentum 冲量(0.001) | 0.4371 |
Adam优化器表现很差,梯度下降优化器表现一般,Momentum优化器在冲量0.9时表现较好,但随着冲量减小,正确率也在减小。
3.4 改变BATCH_SIZE
| BATCH_SIZE | 在测试集的准确率 |
|---|---|
| 1000 | 0.7315 |
| 100 | 0.7407 |
| 10000 | 0.6896 |
当BATCH_SIZE为100时,在14轮之后,学习率变为了0。
四、总分析
主要使用mnist2.py。做了三种不同结构的网络,其中第二种三层网络在测试集上的表现最好,但这可能由于第二种做的比较完善,但是可以去推想,即使增加模型隐藏层层数,并不一定能提高模型在测试集上的表现,根据前面更改节点个数,同样得出,增加节点个数不一定能提高正确率,但是增加节点数会增长程序运行时间!
通过对前面的探究,初步得出,对模型影响比较大的两个因素 学习率和损失函数。
学习率不可设置的过大或过小,要根据实际情况选择。
损失函数选择非常重要,不同的损失函数对模型影响很大,若选择不好,有可能导致loss不收敛,或模型表现非常差!