优化问题|生产车间布局优化问题及遗传算法求解（MATLAB）

问题描述

生产车间布局优化的主要目标是实现作业单位间非物流关系的最大化和物料搬运成本的最小化，并由此作出如下合理假设：

1. 所有作业单位所在平面为共平面;

2. 各单位形状均为矩形，忽略形状细节，且各个矩形边与 X 轴、Y 轴平行;

3. 不同作业单位间单位运输成本一致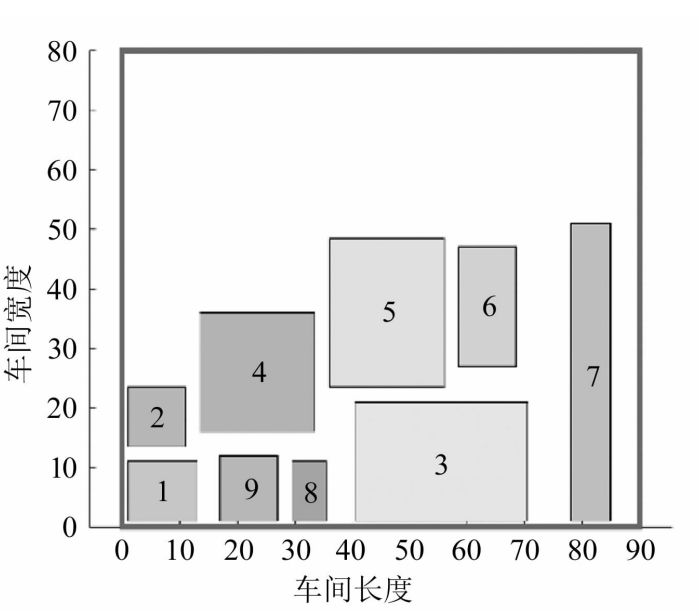

数学模型

参数变量

C 1 C_1 C1: 总搬运成本

C 2 C_2 C2: 非物流关系总和

c i j c_ij cij：各作业单元之间的搬运成本

T i j T_ij Tij：各作业单元之间非物流关系的紧密程度

b i j b_ij bij: 各作业单元之间非物流关系的关联因子

x i , y i x_i, y_i xi,yi：作业单元 i i i的X轴、Y轴中心坐标

L i , W i L_i, W_i Li,Wi：作业单元 i i i的长度和宽度

L , W L, W L,W：作业车间的长度和宽度

目标函数

目标函数为作业单位间非物流关系的最大化和物料搬运成本的最小化

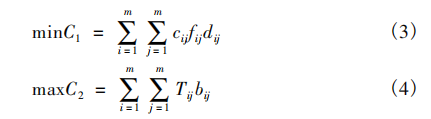
将双目标转化为单目标优化问题：

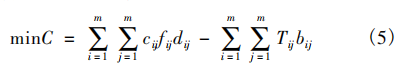
约束条件

作业单位之间不能重叠

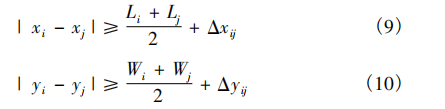
各作业单元不超出车间的边界范围

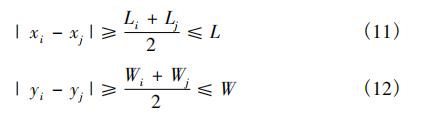
遗传算法求解

编码规则

基因编码包括两部分：一部分为每个作业单元的中心坐标编码，一部分为每个作业单元的摆放方向（0-1编码，1表示水平放置，0表示竖直放置）

选择方式

采用轮盘赌方法选择个体保留进入下一代循环，其中即个体被选中的概率与其适应度

值大小存在一定的比例关系，适应度值越高，占比越大，被选中的概率就越大

交叉和变异

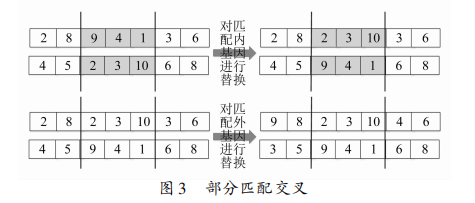
部分匹配交叉方式进行交叉操作

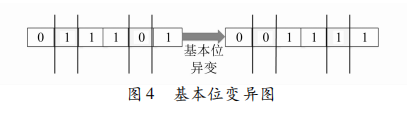
基本位变异方式，即随机产生变异位进行二进制变异

部分代码展示

变异操作

% 输入参数：
% x: 种群编码
% Gnum： 作业单元数量
% gap: 设备与边界的间距
% dist: 设备间的间距
% LWO: 作业单元的尺寸
% L, W：车间尺寸

function f0 = Mutate(x,Gnum,dim,gap,dist,LW0,L,W,minbound,maxbound,big)

    n = numel(x);
    f0 = x;

    try_num_sum = 500;
    trys = 0;
    flag = 0;
    while flag == 0
        pos=randi([1,n]); %选择变异位点
        if pos <= dim
            v=maxbound(pos)-minbound(pos);
            v0= rand*v;%变异选择位点的值
            while x(pos)==v0
                v0= rand*v;
            end
            f0(pos)=v0;
            f0(1) = L/2;
        else
            f0(pos)=1-x(pos);
            f0(dim+1)=0;
        end
        p = [f0(1:Gnum); f0(Gnum+1:dim)]';
        y = f0(dim+1:end);
        LW= LW0;
        for k = 1 : Gnum
            LW(k,1) = y(k)*LW0(k,1)+(1-y(k))*LW0(k,2);
            LW(k,2) = (1-y(k))*LW0(k,1)+y(k)*LW0(k,2);
        end
        flag1 = isInRange_1(p,gap,LW,L,W);
        flag2 = nonoverlap(p,dist,LW,big);
        flag=flag1*flag2;

        trys = trys + 1;
        if(trys>try_num_sum)
            f0 = x;
            break;
        end
    end
end

结果展示

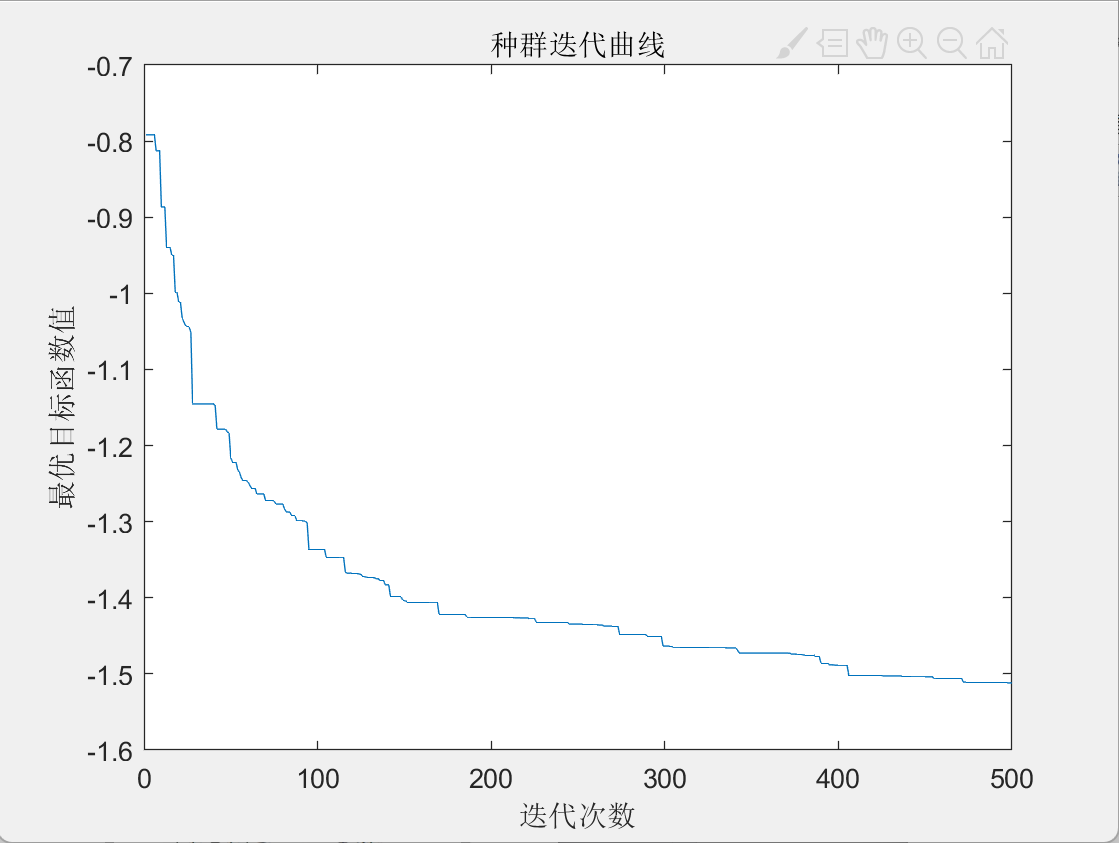
迭代曲线

布局图

参考文献

闫向彤,张永鑫,李佩泽,等.基于遗传算法的车间布局优化研究[J].机械设计与制造工程,2021,50(09):88-92.