数据结构之三：栈和队列

线性表：有个n个元素的集合，逻辑上成线性结构。（顺序表、链表、栈、队列、串）。

栈

栈：一种特殊的线性表，其只允许在固定的一端进行插入和删除元素操作。

进行数据插入和删除操作的一端称为栈顶，另一端称为栈底。

栈中的数据元素遵守后进先出LIFO（Last In First Out）的原则。

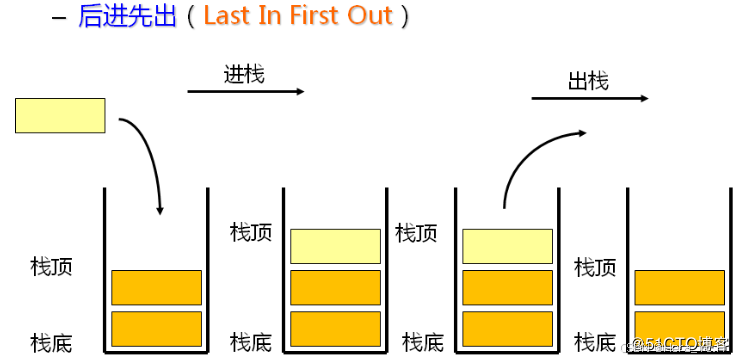
数组来实现：

链表来实现：

如果是双向链表，那么哪边是栈顶，哪边是栈底都无所谓。
如果是单链表：

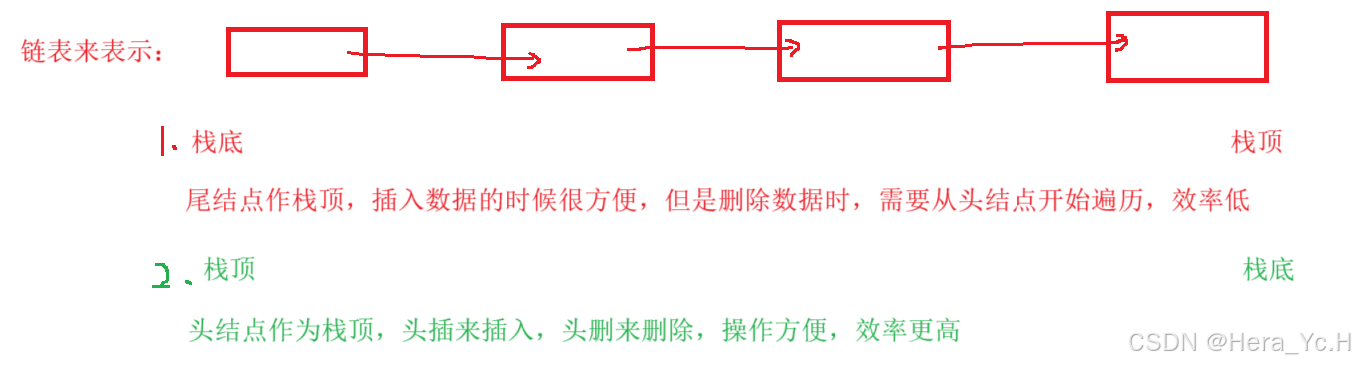
实现栈 ：数组更加简单（对于当代的计算机，内存开辟带来的时间开销可以忽略不计）。

头文件

cpp 复制代码

#pragma once
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>

typedef int STDataType;
#define N 4

/*
静态
struct Stack
{
	int* _a[N};
	int _size;//
};
*/
typedef struct Stack
{
	STDataType* _a;
	int _top;		//栈顶下标
	int _capacity;	//容量
}Stack;

void StackInit(Stack* pst);
void StackDestory(Stack* ppst);
void StackPush(Stack* pst, STDataType x);
void StackPop(Stack* pst);
int StackSize(const Stack* pst);

//返回1是空，返回0是非空
int StackEmpty(Stack* pst);
//获取栈顶数据
STDataType StackTop(Stack* pst);

实现

cpp 复制代码

#define _CRT_SECURE_NO_WARNINGS

#include "stack.h"

void StackInit(Stack* pst)
{
	assert(pst);
	pst->_a = (STDataType*)malloc(sizeof(int) * N);
	pst->_capacity = N;
	pst->_top = 0;
	//初始0：top在栈顶的下一个位置
	//初始1：top在栈顶位置
}

void StackDestory(Stack* pst)
{
	assert(pst);
	free(pst->_a);
	pst->_a = NULL;
	pst->_capacity = 0;
	pst->_top = -1;

}

void StackPush(Stack* pst, STDataType x)
{
	assert(pst);
	if (pst->_top == pst->_capacity)
	{
		pst->_capacity *= 2;
		STDataType* tmp= (STDataType*)realloc(pst->_a, sizeof(STDataType) * pst->_capacity);
		if (tmp == NULL)
		{
			printf("内存不足\n");
			exit(-1);
		}
		else
		{
			pst->_a = tmp;
		}
	}
	pst->_a[pst->_top] = x;
	pst->_top++;
}

void StackPop(Stack* pst)
{
	assert(pst);
	assert(pst->_top > 0);
	//if(pst->_top>0)
	pst->_top--;
}

int StackSize(const Stack* pst)
{
	assert(pst);
	return pst->_top;
}
STDataType StackTop(Stack* pst)
{
	assert(pst);
	assert(pst->_top > 0);
	return pst->_a[pst->_top - 1];
}
int StackEmpty(Stack* pst)
{
	assert(pst);
	return !pst->_top;
}

队列

队列：只允许在一端进行插入数据操作，在另一端进行删除数据操作的特殊线性表。

队列具有先进先出FIFO(First In First Out)

入队列 ：进行插入操作的一端称为队尾。
出队列 ：进行删除操作的一端称为队头。

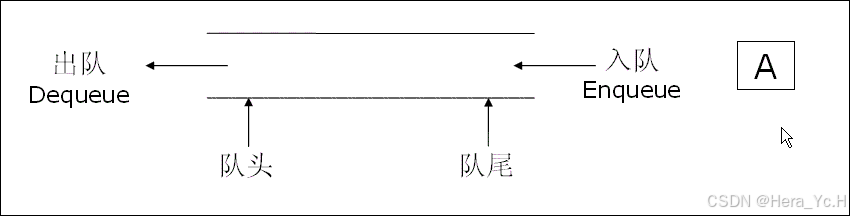
数组来实现：无论是哪一边做队头，都需要挪动数据，开销大效率低。（不挪动数据相对复杂）。

链表实现：

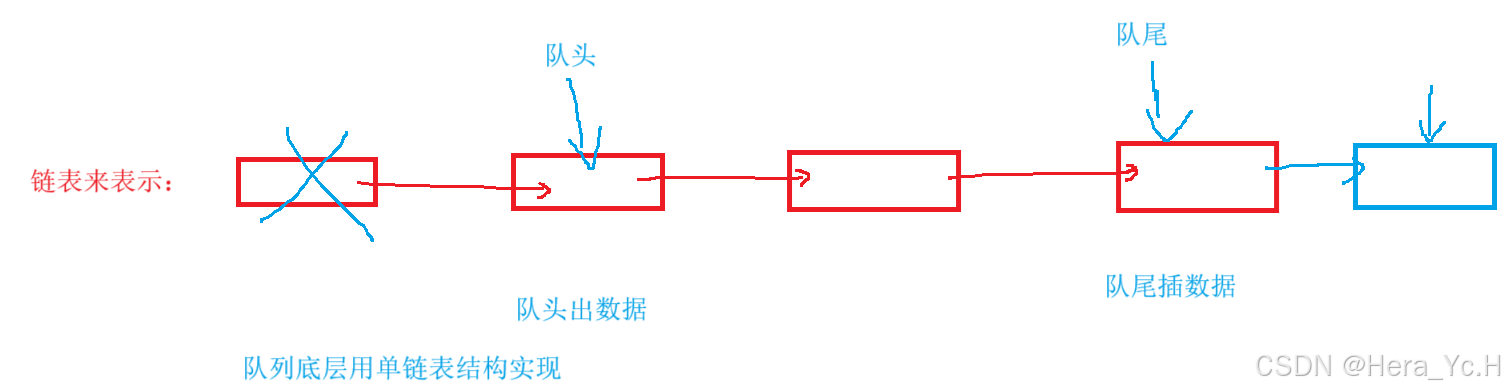
头文件

cpp 复制代码

#pragma once
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>

typedef int QDataType;

typedef struct QueueNode
{
	struct QueueNode* _next;
	QDataType _data;
}QueueNode;

typedef struct Queue
{
	QueueNode* _head;
	QueueNode* _tail;
}Queue;


void QueueInit(Queue* pq);
void QueueDestory(Queue* pq);
//出入队
void QueuePush(Queue* pq, QDataType x);
void QueuePop(Queue* pq);
QDataType QueueFront(Queue* pq);
QDataType QueueBack(Queue* pq);


//返回1是空，返回0是非空
int QueueEmpty(Queue* pst);
//获取栈顶数据
QDataType QueueTop(Queue* pst);

实现

cpp 复制代码

#define _CRT_SECURE_NO_WARNINGS
#include "queue.h"

void QueueInit(Queue* pq)
{
	assert(pq);
	pq->_head = pq->_tail = NULL;
}
void QueueDestory(Queue* pq)
{
	assert(pq);
	QueueNode* cur = pq->_head;
	while (cur)
	{
		QueueNode* next = cur->_next;
		free(cur);
		cur = next;
	}
	pq->_head = pq->_tail = NULL;
}
//出入队
void QueuePush(Queue* pq, QDataType x)
{
	assert(pq);
	QueueNode* newnode = (QueueNode*)malloc(sizeof(QueueNode));
	if (newnode == NULL)
	{
		exit(-1);
	}
	newnode->_data = x;
	newnode->_next = NULL;
	if (pq->_head == NULL)
	{
		pq->_head = pq->_tail = newnode;
	}
	else
	{
		pq->_tail->_next = newnode;
		pq->_tail = newnode;
	}
}
void QueuePop(Queue* pq)
{
	assert(pq);
	assert(pq->_head);
	QueueNode* next = pq->_head->_next;
	free(pq->_head);
	pq->_head = next;
	if (pq->_head == NULL)
	{
		pq->_tail = NULL;
	}
}
QDataType QueueFront(Queue* pq)
{
	assert(pq&&pq->_head);
	return pq->_head->_data;
}
QDataType QueueBack(Queue* pq)
{
	assert(pq && pq->_tail);
	return pq->_tail->_data;
}


//返回1是空，返回0是非空
int QueueEmpty(Queue* pq)
{
	return pq->_head == NULL ? 1 : 0;
}
//获取栈顶数据
QDataType QueueTop(Queue* pq)
{
	assert(pq);
	int sz = 0;
	QueueNode* cur = pq->_head;
	while (cur)
	{
		sz++;
		cur = cur->_next;
	}
	return sz;
}

数据结构的栈和堆和内存中的堆栈有什么区别?

数据结构的栈、堆：**存储和管理数据，**解决一些一些问题。

内存中的堆栈：虚拟进程地址空间分段。一段内存区域的划分。

数据结构的栈和内存的栈都满足"后进先出"的规则。

循环队列

循环队列用数组实现更容易判断队列的空满。

cpp 复制代码

typedef struct {
    int*_a;
    int front;
    int rear;
    int k;
} MyCircularQueue;

bool myCircularQueueIsFull(MyCircularQueue* obj);
MyCircularQueue* myCircularQueueCreate(int k) {
    MyCircularQueue* q=(MyCircularQueue*)malloc(sizeof(MyCircularQueue));
    q->_a=(int*)malloc(sizeof(int)*(k+1));
    q->front=q->rear=0;
    q->k=k;
    return q;
}

bool myCircularQueueEnQueue(MyCircularQueue* obj, int value) {
    if(myCircularQueueIsFull(obj))
    {
        return false;
        
    }
    else
    {
        obj->_a[obj->rear]=value;
        obj->rear = (obj->rear+1)%(obj->k+1);
        return true;
    }
    
}

bool myCircularQueueDeQueue(MyCircularQueue* obj) {
    if(obj->front==obj->rear)
    {
        return false;
    }
    else
    {
        obj->front = (obj->front+1)%(obj->k+1);
        return true;
    }
}

int myCircularQueueFront(MyCircularQueue* obj) {
    if(obj->front==obj->rear)
    {
        return -1;
    }
    return obj->_a[obj->front];
}

int myCircularQueueRear(MyCircularQueue* obj) {
    if(obj->front==obj->rear)
    {
        return -1;
    }
    int tail=obj->rear-1;
    if(tail==-1)
    {
        tail=obj->k;
    }
    return obj->_a[tail];
}


bool myCircularQueueIsEmpty(MyCircularQueue* obj) {
    return obj->front==obj->rear;
}

bool myCircularQueueIsFull(MyCircularQueue* obj) {
    return (obj->rear+1)%(obj->k+1)==obj->front;
}

void myCircularQueueFree(MyCircularQueue* obj) {
    free(obj->_a);
    free(obj);
}