目录

1、插入排序

void InsertSort(int* arr, int n)
{
int i = 0;
for (int i = 0; i + 1 < n; i++)
{
int end = i;
int tmp = arr[end + 1];
while (end >= 0)
{
if (arr[end] > tmp)
{
arr[end + 1] = arr[end];
end--;
}
else
{
break;
}
}
arr[end + 1] = tmp;
}
}另一种写法
INSERTION-SORT
源码
for j=2 to A.legth
key=A[j]
i=j-1
whlie i>0 and A[i]>key
A[i+1]=A[i]
i=i-1
A[i+1]=key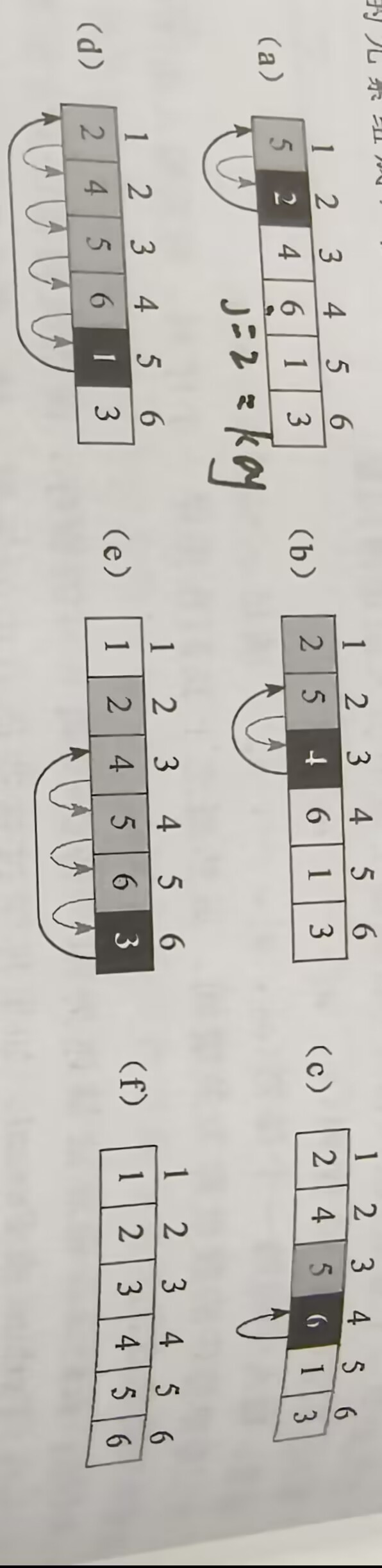

插入排序
比方说手上有6张扑克牌-5 2 4 6 1 3通过插入排序
即从j=2开始(key=2)比较key与A[i] (i=j-1也就是2这张牌的前一张牌5比较)并完成交换数值
把第一张key排好后j++=3再来循环
c语言实现
#include<stdio.h>
int main()
{
int j ;
int arr[6] = { 5,2,4,6,1,3 };
int sz = sizeof(arr) / sizeof(arr[0]);
for (j=1; j < sz; j++)
{
int key = arr[j];
int i = j - 1; //arr[i]>arr[j]不行吗
while (i >=0 && arr[i] > key)//升序排列
{
arr[i + 1] = arr[i];//为什么不能写成arr[j]=arr[i]
i = i - 1;
}
arr[i + 1] = key;
}
return 0;
}- arr[i]比较的是key的值,而不是arr[j]的值,因为arr[j]在while循环中会改变
- 同理
2、希尔排序
希尔排序法⼜称缩⼩增量法。希尔排序法的基本思想是:先选定⼀个整数(通常是gap=n/3+1),把 待排序⽂件所有记录分成各组,所有的距离相等的记录分在同⼀组内,并对每⼀组内的记录进⾏排 序,然后gap=gap/3+1得到下⼀个整数,再将数组分成各组,进⾏插⼊排序,当gap=1时,就相当于 直接插⼊排序。它是在直接插⼊排序算法的基础上进⾏改进⽽来的,综合来说它的效率肯定是要⾼于直接插⼊排序算法的。

每一组的排序都是插入排序
int gap = n / 3 + 1;
for (int i = 0; i + gap < n; i+gap)
{
int end = i;
int tmp = arr[end + gap];
while (end >= 0)
{
if (arr[end] > tmp)
{
arr[end + gap] = arr[end];
end-=gap;
}
else
{
break;
}
}
arr[end + gap] = tmp;
}完整代码
void ShellSort(int* arr, int n)
{
int i = 0;
int gap = n;
while (gap > 1)
{
gap = gap/3 +1;
for ( i = 0; i + gap < n; i ++)
{
int end = i;
int tmp = arr[end + gap];
while (end >= 0)
{
if (arr[end] > tmp)
{
arr[end + gap] = arr[end];
end -= gap;
}
else
{
break;
}
}
arr[end + gap] = tmp;
}
}
}3、堆排序
void AdjustDown(DataType* arr, int parent, int n)
{
int child = 2 * parent + 1;
while (child < n)
{
if (child + 1 < n && arr[child] < arr[child + 1])
{
child++;
}
if (arr[child] > arr[parent])
{
Swap(&arr[child], &arr[parent]);
parent = child;
child = 2 * child + 1;
}
else
{
break;
}
}
}
void HeapSort(int* arr, int n)
{
int i = 0;
//用向下调整算法建堆
//循环从下至上
for (i = (n - 1 - 1) / 2; i >= 0; i--)
{
AdjustDown(arr, i, n);
}
int end = n - 1;
while (end > 0)
{
Swap(&arr[0], &arr[end]);
AdjustDown(arr, 0, end);
end--;
}
}4、直接选择排序
未优化
void SelectSort1(int* arr, int n)
{
int mini;
for (int i = 0; i < n - 1; i++)
{
mini = i;
for (int j = i + 1; j < n; j++)
{
if (arr[j] < arr[mini])
{
mini = j;
}
}
Swap(&arr[i], &arr[mini]);
}
}优化
void SelectSort(int* arr, int n)
{
int begin = 0;
int end = n - 1;
while (begin < end)
{
int maxi = begin, mini = begin;
for (int i = begin + 1; i <= end; i++)
{
if (arr[i] > arr[maxi])
{
maxi = i;
}
if (arr[i] < arr[mini])
{
mini = i;
}
}
if (begin == maxi)
{
maxi = mini;
}
Swap(&arr[begin], &arr[mini]);
Swap(&arr[end], &arr[maxi]);
++begin;
--end;
}
}5、快排
快速排序是Hoare于1962年提出的⼀种⼆叉树结构的交换排序⽅法,其基本思想为:任取待排序元素 序列中的某元素作为基准值,按照该排序码将待排序集合分割成两⼦序列,左⼦序列中所有元素均⼩ 于基准值,右⼦序列中所有元素均⼤于基准值,然后最左右⼦序列重复该过程,直到所有元素都排列 在相应位置上为⽌。

int _QuickSort(int* arr, int left, int right)
{
//left从左往右找比基准值大的数据
//right从右往左找比基准值小的数据
int keyi = left;
left++;
while (left <= right)
{
while (left <= right &&arr[left] < arr[keyi])
{
left++;
}
//left找到了最大位置
while (left <= right &&arr[right] > arr[keyi])
{
right--;
}
if (left <= right)
{
Swap(&arr[left++], &arr[right--]);
}
}
Swap(&arr[keyi], &arr[right]);
return right;
}
//双指针法
int _QuickSort3(int* arr, int left, int right)
{
int key = left, slow = left, fast = left + 1;
while (fast <= right)
{
if (arr[fast] < arr[key] && ++slow != fast)
{
Swap(&arr[slow], &arr[fast]);
}
fast++;
}
Swap(&arr[key], &arr[slow]);
return slow;
}
void QuickSort(int* arr, int left, int right)
{
if (left >= right)
{
return;
}
int keyi= _QuickSort(arr, left, right);
QuickSort(arr, left,keyi-1);
QuickSort(arr, keyi+1, right);
}6、归并排序
void _MergeSort(int* arr,int left,int right,int* tmp)
{
if (left >= right)
{
return;
}
int mid = (left + right) / 2;
//[left,mid] [mid+1,right]
_MergeSort(arr, left, mid, tmp);
_MergeSort(arr, mid + 1, right, tmp);
//合并
//[left,mid] [mid+1,right]
int begin1 = left, end1 = mid;
int begin2 = mid + 1, end2 = right;
int index = begin1;
while (begin1 <= end1 && begin2 <= end2)
{
if (arr[begin1] < arr[begin2])
{
tmp[index++] = arr[begin1++];
}
else {
tmp[index++] = arr[begin2++];
}
}
//要么begin1越界 要么begin2越界
while (begin1 <= end1)
{
tmp[index++] = arr[begin1++];
}
while (begin2 <= end2)
{
tmp[index++] = arr[begin2++];
}
//[left,mid] [mid+1,right]
//把tmp中的数据拷贝回arr中
for (int i = left; i < right; i++)
{
arr[i] = tmp[i];
}
}
void MergeSort(int* arr, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
_MergeSort(arr, 0, n - 1, tmp);
free(tmp);
}