【PyTorch】回归问题代码实战

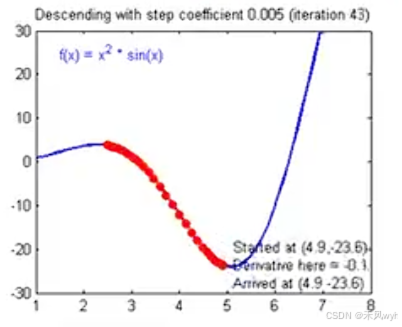
梯度下降法是优化算法中一种常用的技术，用于通过最小化损失函数来求解模型的最优参数。在线性回归中，目标是通过拟合数据来找到一条最适合的直线。梯度下降法通过迭代地调整模型参数，使得损失函数（通常是均方误差）最小化，从而找到最优的参数。

线性回归的目标是根据输入特征 x 预测输出 y。假设我们有一个输入特征 x 和对应的输出标签 y，线性回归模型可以用以下公式表示：

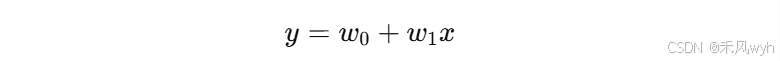
给定一组数据集, 我们的目标是通过调整权重和，使得模型的预测值与真实值之间的误差最小。首先对参数进行求梯度：

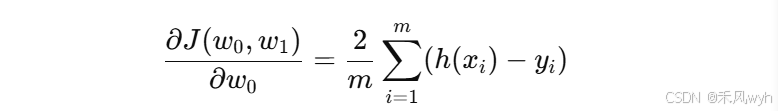
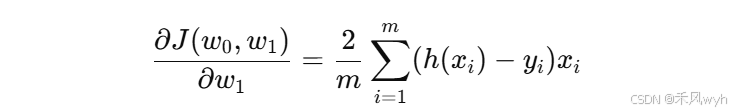
通过计算梯度，我们知道了损失函数在每个参数方向上的变化趋势。为了最小化损失函数，我们沿着梯度的反方向更新参数。参数更新的公式为：

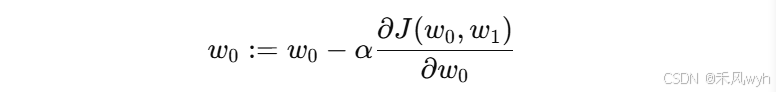
采用MSE计算损失函数，损失函数为，那么更新后的参数为，其中,

计算损失函数：

python 复制代码

def compute_error_for_line_given_points(b,w,points):
    totalError = 0
    for i in range(0, len(points)):
        x = points[i,0]
        y = points[i,1]
        totalError += (y-(w*x+b))**2
    return totalError/float(len(points))

计算梯度值：

python 复制代码

def step_grdient(b_current, w_current, points, learningRate):
    b_gradient = 0
    w_gradient = 0
    N = float(len(points))
    for i in range(0, len(points)):
        x = points[i, 0]
        y = points[i, 1]
        b_gradient += -(2/N) * (y - ((w_current * x) + b_current))
        # 梯度信息多了一个x
        w_gradient += -(2/N) * x * (y - ((w_current * x) + b_current))
    new_b = b_current - (learningRate * b_gradient)
    new_w = w_current - (learningRate * w_gradient)
    return [new_b, new_w]

循环计算梯度：

python 复制代码

def gradient_descent_runner(points, starting_b, starting_m, learning_rate, num_iterations):
    b = starting_b
    w = starting_w
    for i in range(num_iterations):
        b, w = step_gradient(b, w, np.array(points), learning_rate)
    return [b, w]

进行运行：

python 复制代码

def run():
    points = np.genfromtext("data.csv", delimiter=",")
    learining_rate = 0.0001
    initial_b = 0
    initial_w = 0
    num_iterations = 100
    print("Starting gradient descent at b={0}, w={1},error={2}".format(initial_b, initial_m, compute_errror_for_line_given_points(initial_b, initial_w, points)))
    print("Running......")
    [b, w] = gradient_descent_runner(points, initial_b, initial_w, learning_rate, num_iterations)
    print("After {0} iterations b = {1}, w = {2}, error = {3}".format(num_iterations, b, m))

参考资料：
6.6 回归问题实战6_哔哩哔哩_bilibilihttps://www.bilibili.com/video/BV1RiDJYmEEU?spm_id_from=333.788.videopod.episodes&vd_source=0dc0c2075537732f2b9a894b24578eed&p=9