一,setAll功能哈希表
要求使用setall方法时,哈希表里的所有键值对的值全部改变成一样。例如,使用setall将值全部设置为1.
但是又有要求,不能遍历哈希表,只能是常数时间。
原理
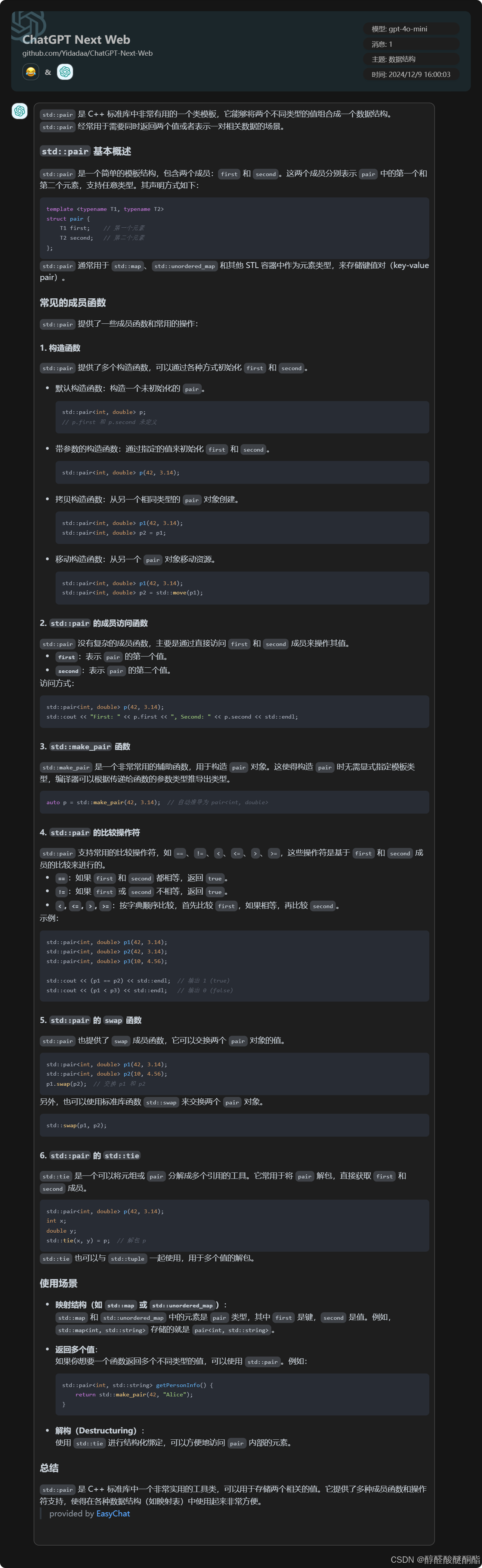
值不再是单纯一个int类型的数字,改为pair类型,储存原来的值和存入哈希表的时间。
同时设置两个变量,一个记录setall值,一个记录setall时间。每次访问哈希表时通过比较存入的时间和setall时间哪个更新,决定值是哪一个。
补充
代码
cpp
#include<iostream>
#include<unordered_map>
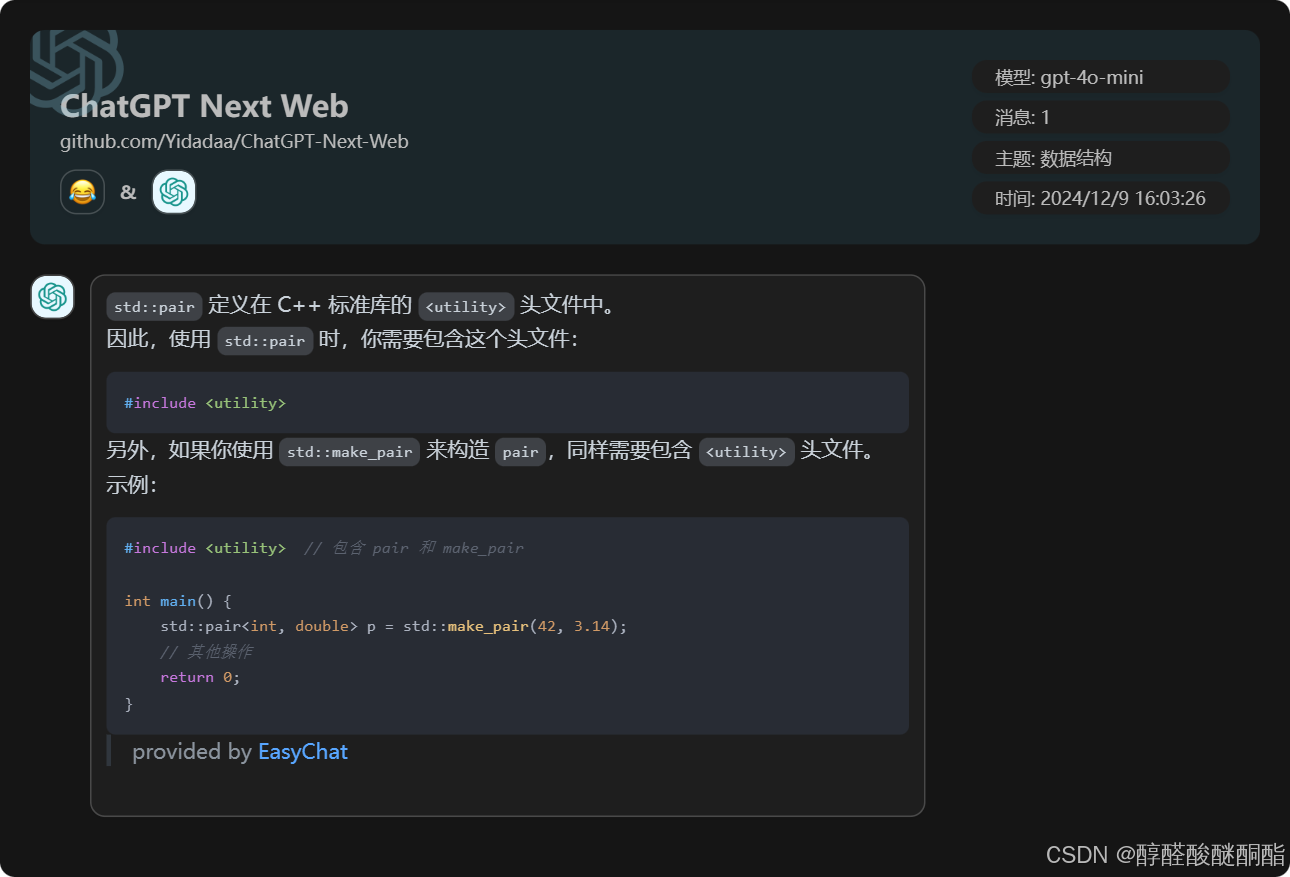
#include<utility>
using namespace std;
class SetAll
{
public:
int time;
int setall_time;
int setall_value;
unordered_map<int, pair<int, int>> map;
SetAll() : time(0),setall_time(0),setall_value(0) {};
void insert(int key, int value)
{
time = time < setall_time ? setall_time : time;
map[key] = { value,++time };
}
void setall(int value)
{
setall_value = value;
setall_time = ++time;
}
int find(int key)
{
return map[key].second < setall_time ? setall_value : map[key].first;
}
};
int main()
{
SetAll setall_map;
setall_map.insert(5, 10);
setall_map.insert(3, 6);
setall_map.setall(7);
setall_map.insert(4, 8);
cout << setall_map.find(5) << endl;
cout << setall_map.find(4) << endl;
return 0;
}如果不想用pair可以使用int数组。
二,实现LRU结构
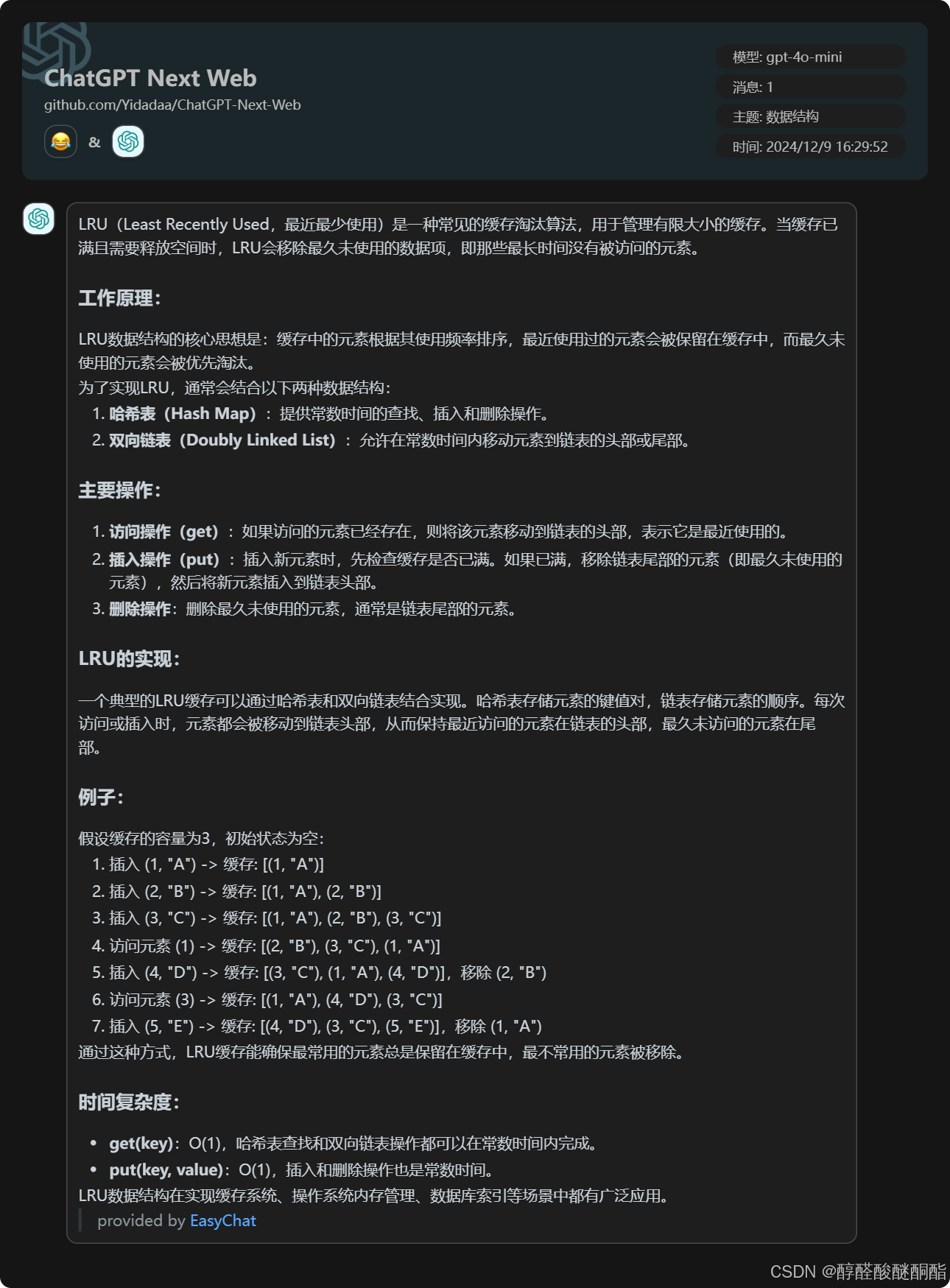
一,只是用链表实现
增的操作时间复杂度都是O(1),而删,查找的时间复杂度就是O(n)。
cpp
#include<iostream>
using namespace std;
class LRU
{
public:
int capability;
int consumption;
struct Node
{
int key;
int value;
Node* next;
};
Node* head;
LRU(int x) :capability(x), consumption(0), head(NULL) {};
void insert(int key, int value)
{
Node* p = new Node;
p->key = key;
p->value = value;
p->next = head;
head = p;
consumption++;
if (consumption > capability)
{
Node* current = head;
while (current->next->next)
{
current = current->next;
}
free(current->next);
current->next = NULL;
consumption--;
}
}
int find(int key)
{
Node* current = head;
Node* pre = NULL;
while (current)
{
if (current->key == key)
{
if (!pre)
{
return current->value;
}
int ans = current->value;
//先记录答案,因为后面要改变节点。
pre->next = current->next;
current->next = head;
head = current;
return ans;
}
pre = current;
current = current->next;
}
return -1;
}
void dele(int key)
{
if (!head) return;
Node* current = head;
Node* pre = NULL;
if (current->key == key)
{
head = current->next;
free(current);
consumption--;
return;
}
while (current)
{
if (current->key == key)
{
pre->next = current->next;
free(current);
consumption--;
return;
}
pre = current;
current = current->next;
}
}
};
int main()
{
LRU container(3);
for (int i = 0; i < 5; i++)
{
container.insert(i, i * i);
}
for (int i = 0; i < 5; i++)
{
cout << container.find(i) << " ";
}
int ans = container.find(2);
container.insert(10, 10);
cout << container.find(3);
return 0;
}我也是看AI给的答案,我从中明白少用current->next->key,current->next->next这类表达,因为可能会导致引用空指针,所以使用一个变量来记录前一个节点。
二,使用哈希表实现
利用映射关系,将键和节点的地址联系起来,这样查找时就可以直接访问到节点,不用遍历。
我们需要双向链表,准备头和尾节点来记录最早和最晚的节点。
cpp
#include<iostream>
#include<unordered_map>
using namespace std;
struct Node
{
int value;
int key;
Node* last;
Node* next;
Node(int x,int y) : key(x), value(y), last(NULL), next(NULL) {};
};
class LRU
{
public:
int capacity;
int consumption;
Node* head;
Node* tail;
unordered_map<int, Node*> map;
LRU(int x) : capacity(x), head(NULL), tail(NULL), consumption(0) {};
void insert(int key, int value)
{
Node* p = new Node(key,value);
map[key] = p;
consumption++;
if (tail)
{
tail->next = p;
p->last = tail;
tail = p;
}
else
{
head = tail = p;
}
if (consumption > capacity)
{
map.erase(head->key);
head = head->next;
delete head->last;
head->last = NULL;
consumption--;
}
}
int find(int key)
{
auto it = map.find(key);
if (it == map.end()) return -1;
Node* p = it->second;
if (p->last&&p->next)
{
p->last->next = p->next;
p->next->last = p->last;
p->last = tail;
tail->next = p;
tail = p;
}
else if (p->next)
{
head = p->next;
tail->next = p;
p->last = tail;
tail = p;
p->next = NULL;
}
return p->value;
}
};
int main()
{
LRU container(1);
for (int i = 0; i < 5; i++)
{
container.insert(i, i * i);
}
for (int i = 0; i < 5; i++)
{
cout << container.find(i) << " ";
}
return 0;
}我有点感触是尽量将代码函数化,在设计算法时,先构思主结构,需要哪些功能,在去设计子函数。
三,插入,删除和获取随机元素O(1)时间且不允许有重复数字结构
类似hashset,但要求能够返回随机值。
代码
cpp
#include<iostream>
#include<unordered_map>
#include<random>
#include<vector>
using namespace std;
random_device rd;
mt19937 gen(rd());
class Container
{
public:
int size;
unordered_map<int, int> map;
vector<int> vec;
Container() : size(0){};
void insert(int x)
{
if (map.find(x) == map.end())
{
map[x] = size++;
vec.push_back(x);
}
}
void remove(int x)
{
if (vec.empty())
{
cout << "error" << endl;
return;
}
if (map.find(x) == map.end())
{
cout << "error" << endl;
return;
}
//通过覆盖x从而实现删除。同时还要删除尾部元素,避免重复。
int tail = vec.back();
if (x != tail)
{
map.find(tail)->second = map.find(x)->second;
vec[map.find(x)->second] = tail;
}
vec.pop_back();
map.erase(x);
size--;
}
void print_vec()
{
for (int i = 0; i < vec.size(); i++) cout << vec[i] << " ";
cout << endl;
}
int get_random()
{
if (size == 0) return -1;
uniform_int_distribution<int> dis(0, size - 1);
return vec[dis(gen)];
}
};
int main()
{
Container container;
for (int i = 0; i < 5; i++)
{
container.insert(i);
}
container.print_vec();
cout << container.get_random() << endl;
container.remove(3);
container.print_vec();
cout << container.get_random();
container.remove(10);
return 0;
}四,加强版(允许有重复结构)
这样的话我的哈希表的值必须是哈希set,可以储存一系列索引下标。
代码
cpp
#include<iostream>
#include<unordered_map>
#include<unordered_set>
#include<random>
#include<vector>
using namespace std;
random_device rd;
mt19937 gen(rd());
class Container
{
public:
int size;
unordered_map<int, unordered_set<int>> map;
vector<int> vec;
Container() : size(0){};
void insert(int x)
{
if (map.find(x) == map.end())
{
map[x] = { size++ };
vec.push_back(x);
}
else
{
map[x].insert(size++);
vec.push_back(x);
}
}
void remove(int x)
{
if (map.find(x) == map.end())
{
cout << "error" << endl;
return;
}
if (x == vec[size - 1])
{
vec.pop_back();
map.find(x)->second.erase(size - 1);
size--;
return;
}
int index = *map.find(x)->second.begin();
//先用find函数找到要删去值对应的哈希集,然后获取集合中的一个索引。
vec[index] = vec[size-1];
//用向量最后的元素去覆盖。
//然后处理哈希表中的索引
map.find(x)->second.erase(index);
if (map.find(x)->second.empty())
{
map.erase(x);
}
map.find(vec[size - 1])->second.insert(index);
map.find(vec[size - 1])->second.erase(size - 1);
vec.pop_back();
size--;
}
int random_get()
{
uniform_int_distribution<int> dis(0, size - 1);
return vec[dis(gen)];
}
void print_vec()
{
for (int i = 0; i < vec.size(); i++) cout << vec[i] << " ";
cout << endl;
}
};
int main()
{
Container container;
for (int i = 0; i < 5; i++)
{
container.insert(i);
if (i == 2)
{
for (int j = 0; j < 5; j++)
{
container.insert(i);
}
}
}
container.print_vec();
container.insert(10);
for (int i = 0; i < 10; i++)
{
cout << container.random_get() << endl;
}
container.print_vec();
}五,快速获得数据流的中位数的结构
一个流不断输出数据,存储数据并在调用结构时能够返回中间值。奇数个数,返回中间那个数,偶数个数,返回中间两个数字的平均值。
法一 堆结构实现
补充:堆结构
堆(Heap)是一种特殊的树形数据结构,它满足堆性质:父节点的值要么大于(或小于)其子节点的值。这种性质使得堆的根节点总是最大的(或最小的)元素。
根据堆的性质不同,堆可以分为两种:
- 大根堆(Max Heap):在大根堆中,父节点的值大于其子节点的值。也就是说,根节点是堆中最大的元素。每个节点的值都大于其子节点的值。
- 小根堆(Min Heap):在小根堆中,父节点的值小于其子节点的值。也就是说,根节点是堆中最小的元素。每个节点的值都小于其子节点的值。
堆的常用操作包括:
- 插入(Insert):将一个新元素插入到堆中。
- 删除(Delete):从堆中删除一个元素。
- 提取(Extract):从堆中提取最大的(或最小的)元素。
- 修改(Modify):修改堆中某个元素的值。
堆的应用非常广泛,例如:
- 优先队列(Priority Queue):堆可以用来实现优先队列,优先级最高的元素总是位于队首。
- 排序算法(Sort Algorithm):堆可以用来实现快速排序算法(Heap Sort)。
- 图算法(Graph Algorithm):堆可以用来实现 Dijkstra 算法和 Prim 算法等图算法。
堆的时间复杂度如下:
- 插入:O(log n)
- 删除:O(log n)
- 提取:O(1)
- 修改:O(log n)
其中,n 是堆中的元素个数。
原理
准备一个大根堆和一个小根堆,要保证大小根堆堆顶永远是中间值。如果插入的数字小于大根堆的堆顶进入大根堆,反之进入小根堆。每时每刻保证两个堆的元素个数之差的绝对值不大于1.如果大于了的话,就从多的堆结构拿个放到少的里面。
问题
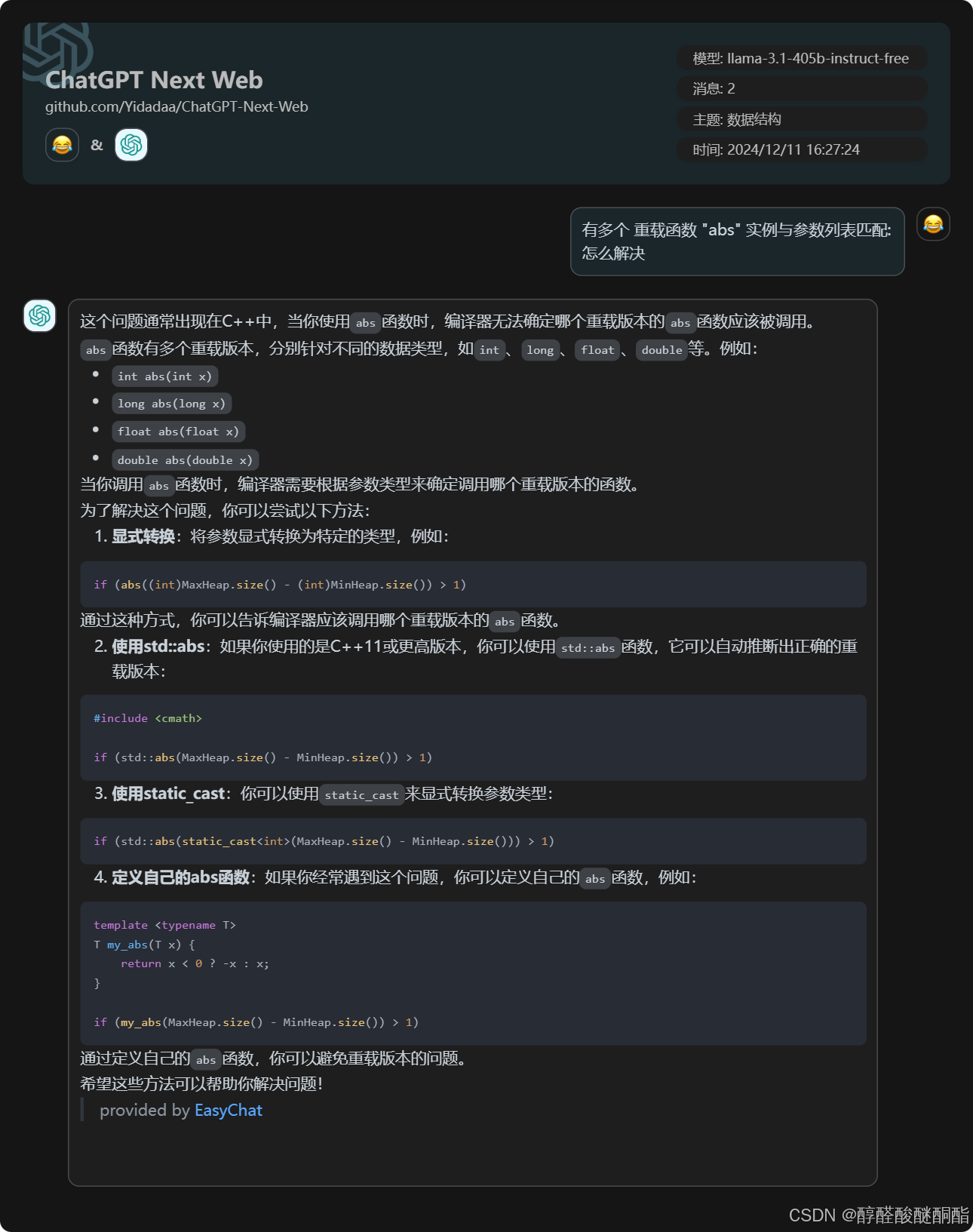
第二个:一定要正确使用if语句,避免反复执行
cpp
void insert(int x)
{
if (MinHeap.empty() && MaxHeap.empty())
{
MaxHeap.push(x);
}
if (x > MaxHeap.top()) MinHeap.push(x);
else MaxHeap.push(x);
if (abs((int)MaxHeap.size() - (int)MinHeap.size()) > 1) balance();
}当MaxHeap和MInHeap为空时,插入x,x会同时进入两个栈中。
代码
我写的
cpp
#include<iostream>
#include<queue>
#include<vector>
using namespace std;
class Mid_Number_Containter
{
public:
priority_queue<int, vector<int>, greater<int>> MinHeap;
priority_queue<int, vector<int>> MaxHeap;
void insert(int x)
{
if (MinHeap.empty() && MaxHeap.empty())
{
MaxHeap.push(x);
}
else if (x > MaxHeap.top()) MinHeap.push(x);
else MaxHeap.push(x);
if (abs((int)MaxHeap.size() - (int)MinHeap.size()) > 1) balance();
}
void balance()
{
if (MaxHeap.size() > MinHeap.size())
{
MinHeap.push(MaxHeap.top());
MaxHeap.pop();
}
else
{
MaxHeap.push(MinHeap.top());
MinHeap.pop();
}
}
double get_mid_number()
{
if (MaxHeap.size() > MinHeap.size()) return MaxHeap.top();
else if (MaxHeap.size() < MinHeap.size()) return MinHeap.top();
else return (double)(MaxHeap.top() + MinHeap.top()) / 2;
}
};
int main()
{
Mid_Number_Containter container;
for (int i = 1; i < 10; i++)
{
container.insert(i);
cout << container.get_mid_number()<< endl;
}
return 0;
}AI写的
cpp
void insert(int x) {
// 如果两个堆都为空,将第一个元素插入到最大堆
if (MaxHeap.empty() && MinHeap.empty()) {
MaxHeap.push(x);
return;
}
// 根据 x 和 MaxHeap 顶部的大小关系,决定插入到哪个堆
if (x <= MaxHeap.top()) {
MaxHeap.push(x);
} else {
MinHeap.push(x);
}
// 平衡两个堆的大小
if (MaxHeap.size() > MinHeap.size() + 1) {
MinHeap.push(MaxHeap.top());
MaxHeap.pop();
} else if (MinHeap.size() > MaxHeap.size()) {
MaxHeap.push(MinHeap.top());
MinHeap.pop();
}
}
cpp
void insert(int x)
{
if (MaxHeap.empty() || x <= MaxHeap.top()) {
MaxHeap.push(x); // 如果x比最大堆的顶部元素小,插入到最大堆
} else {
MinHeap.push(x); // 否则插入到最小堆
}
// 保证最大堆的元素个数多,或者两个堆的大小相等
if (MaxHeap.size() > MinHeap.size() + 1) {
MinHeap.push(MaxHeap.top());
MaxHeap.pop();
} else if (MinHeap.size() > MaxHeap.size()) {
MaxHeap.push(MinHeap.top());
MinHeap.pop();
}
}
double get_mid_number()
{
// 如果两个堆大小相等,返回两个堆顶部元素的平均值;否则返回最大堆顶部元素
if (MaxHeap.size() > MinHeap.size()) return MaxHeap.top();
else return (MaxHeap.top() + MinHeap.top()) / 2.0;
}很多时候AI改你的代码根本不会在你的基础上进行修改,而是直接找数据库里现成的。
六,最大频率栈
定义
最大频率栈(Max Frequency Stack)是一种数据结构,它能够在栈中存储元素,并且能够高效地找到栈中出现频率最高的元素。
最大频率栈通常使用一个哈希表(HashMap)和一个栈(Stack)来实现。哈希表用于存储每个元素的频率,而栈则用于存储元素本身。
最大频率栈的基本操作包括:
push(x): 将元素x推入栈中,并更新哈希表中的频率信息。pop(): 从栈中弹出一个元素,并更新哈希表中的频率信息。maxFrequency(): 返回栈中出现频率最高的元素。
最大频率栈的实现可以使用以下步骤:
- 初始化一个空栈和一个空哈希表。
- 当元素
x被推入栈中时:- 如果
x不在哈希表中,添加x到哈希表中,并设置其频率为 1。 - 如果
x已在哈希表中,增加其频率。 - 将
x推入栈中。
- 如果
- 当元素被弹出栈中时:
- 从栈中弹出一个元素
x。 - 如果
x在哈希表中,减少其频率。 - 如果
x的频率变为 0,移除x从哈希表中。
- 从栈中弹出一个元素
- 当需要找到最大频率元素时:
- 遍历哈希表,找到频率最高的元素。
最大频率栈的时间复杂度为 O(1),空间复杂度为 O(n),其中 n 是栈中元素的数量。
最大频率栈的应用包括:
- 数据压缩:最大频率栈可以用于压缩数据,通过找到出现频率最高的元素,并将其替换为一个较短的代码。
- 缓存:最大频率栈可以用于缓存,通过找到访问频率最高的数据,并将其存储在缓存中。
- 数据分析:最大频率栈可以用于数据分析,通过找到数据中出现频率最高的元素,并进行相应的分析。
使用哈希表和链表来模拟栈
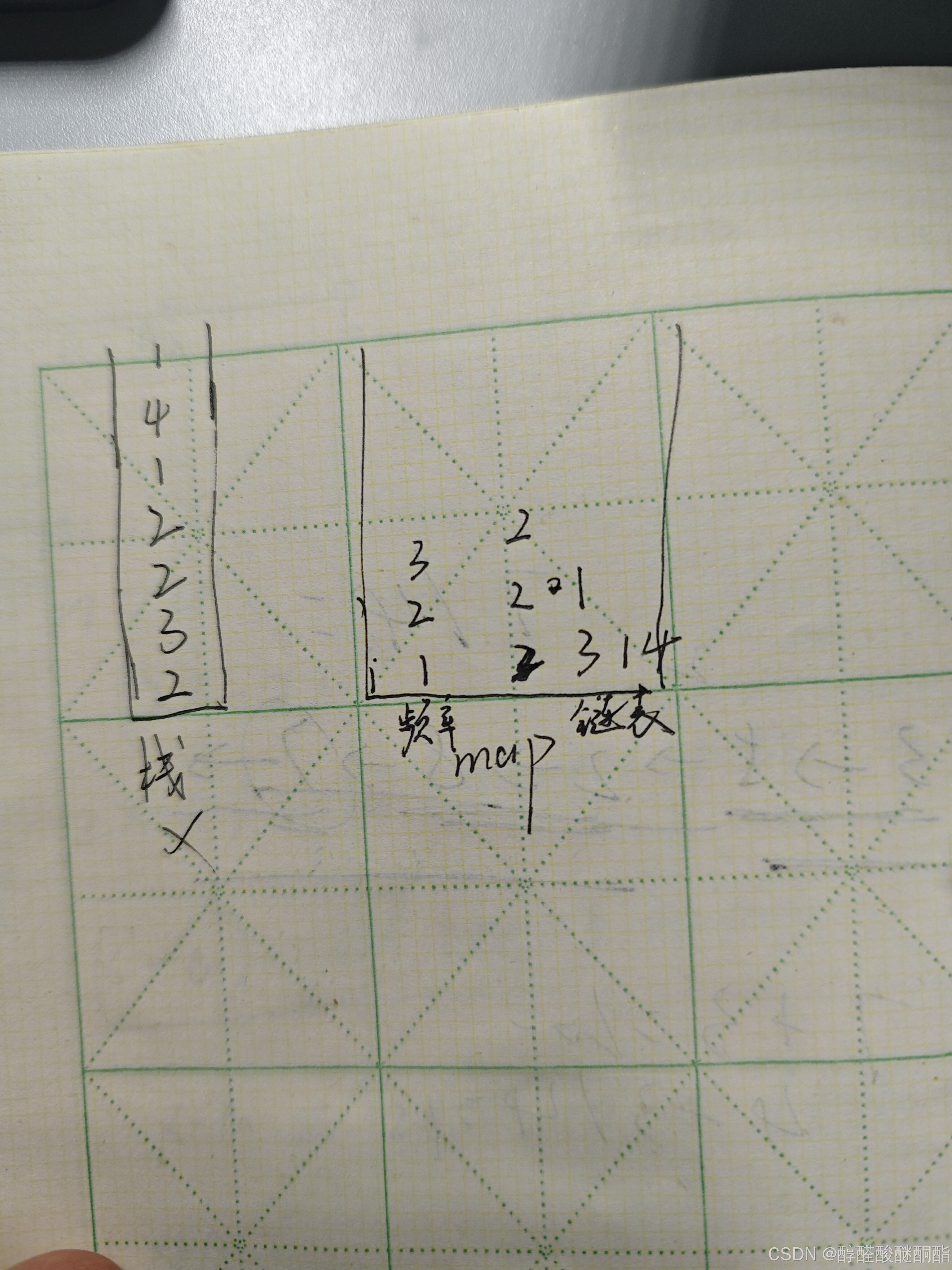
代码
我写的
cpp
#include<iostream>
#include<stack>
#include<unordered_map>
using namespace std;
class MaxFrequencyStack
{
public:
struct Node
{
int value;
Node* next;
Node(int x) : value(x) ,next(NULL){};
};
unordered_map<int, int> map;//记录每个元素出现的次数
unordered_map<int, Node*> maxfreq_stack;
int maxfrequency;
MaxFrequencyStack() : maxfrequency(0) {};
void insert(int x)
{
if (map.find(x) == map.end())
{
map[x] = 1;
}
else
{
map[x]++;
}
maxfrequency = maxfrequency > map[x] ? maxfrequency : map[x];
//下面开始处理最大频率栈。
if (maxfreq_stack.find(map[x]) == maxfreq_stack.end())
{
Node* p = new Node(x);
maxfreq_stack[map[x]] = p;
}
else
{
Node* p = new Node(x);
p->next = maxfreq_stack[map[x]];
maxfreq_stack[map[x]] = p;
}
}
int pop()
{
if (maxfreq_stack.empty()) return -1;
int ans;
Node* node;
node = maxfreq_stack[maxfrequency];
ans = node->value;
if (node->next)
{
maxfreq_stack[maxfrequency] = node->next;
delete node;
map[ans]--;
}
else
{
maxfreq_stack.erase(maxfrequency);
maxfrequency--;
delete node;
}
return ans;
}
};
int main()
{
int arr[] = { 2,3,2,4,3,5,2,1 };
int len = sizeof(arr) / sizeof(int);
MaxFrequencyStack max_freq_stack;
for (int i = 0; i < len; i++)
{
max_freq_stack.insert(arr[i]);
}
for (int i = 0; i < len; i++)
{
cout << max_freq_stack.pop() << " ";
}
return 0;
}AI给的代码
他利用数据结构list省去我写链表的过程
cpp
#include <iostream>
#include <list>
#include <unordered_map>
#include <vector>
class MaxFrequencyStack {
private:
std::list<int> list;
std::unordered_map<int, int> frequency;
std::unordered_map<int, std::vector<std::list<int>::iterator>> positions;
int maxFrequency;
public:
MaxFrequencyStack() : maxFrequency(0) {}
void insert(int x) {
frequency[x]++;
maxFrequency = std::max(maxFrequency, frequency[x]);
list.push_back(x);
positions[x].push_back(--list.end());
}
int pop() {
int x = 0;
for (auto it = list.rbegin(); it != list.rend(); ++it) {
if (frequency[*it] == maxFrequency) {
x = *it;
break;
}
}
auto it = positions[x].back();
positions[x].pop_back();
frequency[x]--;
if (frequency[x] == 0) {
frequency.erase(x);
positions.erase(x);
}
list.erase(it);
if (maxFrequency > 0 && frequency.find(x) == frequency.end() || frequency[x] < maxFrequency) {
maxFrequency = 0;
for (auto& pair : frequency) {
maxFrequency = std::max(maxFrequency, pair.second);
}
}
return x;
}
int getMaxFrequency() {
return maxFrequency;
}
};
int main() {
MaxFrequencyStack stack;
int arr[] = { 2,3,2,4,3,5,2,1 };
int len = sizeof(arr) / sizeof(int);
MaxFrequencyStack max_freq_stack;
for (int i = 0; i < len; i++)
{
max_freq_stack.insert(arr[i]);
}
for (int i = 0; i < len; i++)
{
std::cout << max_freq_stack.pop() << " ";
}
return 0;
}七,全是O(1)的数据结构
往结构里面输入字符串,可以返回计数最多和最少的字符串,要求时间复杂度是常数级的。
up主提供的使用哈希表和双向链表。又要使用到我没有学过的桶结构。
桶结构
学习参考:
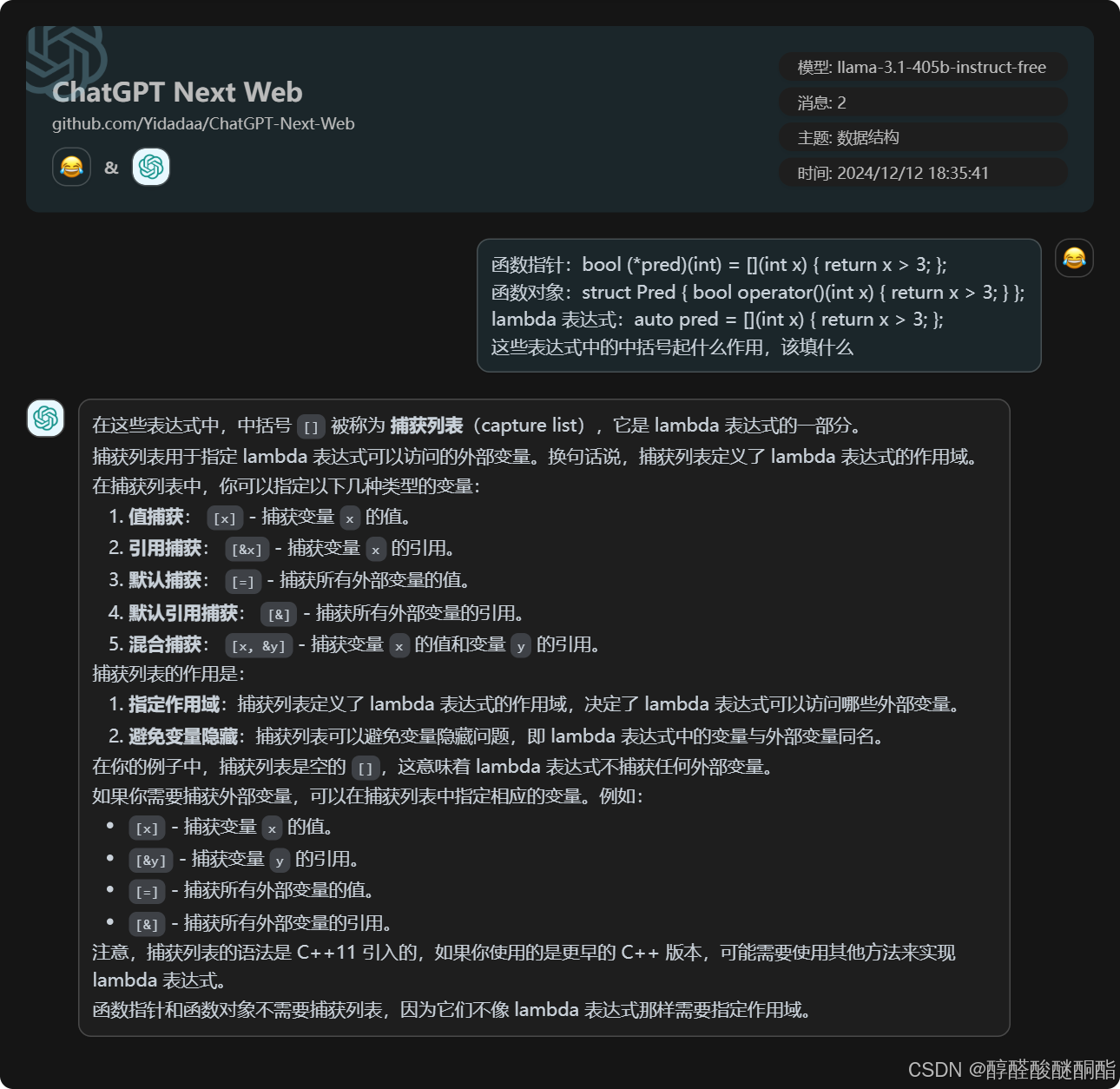
代码
cpp
#include<iostream>
#include<vector>
#include<list>
#include<string>
using namespace std;
class Bucket
{
private:
vector<list<pair<int,string>>> buckets;
size_t hashFunction(int key)
{
return key % buckets.size();
}
public:
Bucket(size_t size = 10) : buckets(size) {}
//初始默认值为10.
void insert(int key, string value)
{
size_t index = hashFunction(key);
buckets[index].push_back({ key,value });
//因为buckets是向量,每个元素都是链表,直接在链表后端接上一对值
}
string search(int key)
{
size_t index = hashFunction(key);
for (const auto& it : buckets[index])
{
if (it.first == key) return it.second;
}
return "not found";
}
//当使用哈希函数时将不同键的值投影到同一索引,我们通过链表解决。
//所以才会有遍历buckets[index],去找键相同的对。
void remove(int key)
{
size_t index = hashFunction(key);
auto& bucket = buckets[index];
bucket.erase(remove_if(bucket.begin(), bucket.end(),
[key](const auto& p) {return p.first == key; }), bucket.end());
}
};
int main()
{
Bucket bucket;
bucket.insert(10, "China");
bucket.insert(20, "America");
bucket.insert(30, "Russia");
bucket.insert(15, "Japan");
bucket.insert(25, "Korea");
bucket.insert(14, "India");
cout << bucket.search(10) << endl;
cout << bucket.search(20) << endl;
bucket.remove(20);
cout << bucket.search(20) << endl;
cout << bucket.search(10) << endl;
return 0;
}题目要求
统计词频,要求能够返回最多出现的字符串
错误
cpp
#define MaxInt 100;宏定义之乱加分号
最终代码
cpp
#include<iostream>
#include<unordered_set>
#include<unordered_map>
#include<string>
#define MaxInt 100
using namespace std;
class AllOne
{
public:
class Bucket
{
public:
unordered_set<string> bucket;
int frequency;
Bucket* last;
Bucket* next;
Bucket(int x,string str) : frequency(x), last(NULL), next(NULL)
{
bucket.insert(str);
};
};
void insert_bucket(Bucket* cur, Bucket* pos)
{
cur->next->last = pos;
pos->next = cur->next;
cur->next = pos;
pos->last = cur;
}
void remove_bucket(Bucket* cur)
{
cur->last->next = cur->next;
cur->next->last = cur->last;
delete cur;
}
Bucket* head;
Bucket* tail;
unordered_map<string, Bucket*> map;
//这个哈希表是储存字符串和对应桶的地址。
AllOne()
{
head = new Bucket(0, "");
tail = new Bucket(MaxInt, "");
head->next = tail;
tail->last = head;
}
void insert(string key)
{
if (map.find(key) == map.end())
//先考虑第一次加入字符串key时,又要分两种情况。
{
if (head->next->frequency != 1)
//当从来没有字符串加入过数据结构时
{
Bucket* newbucket = new Bucket(1, key);
insert_bucket(head, newbucket);
//还要往大类的map里记录加入的字符串
map.insert({ key,newbucket });
}
else //数据结构中有词频为1的桶
{
head->next->bucket.insert(key);
map.insert({ key,head->next });
}
}
else
//如果之前加入过,先查表看key出现过几次。
{
Bucket* temp = map.find(key)->second;
int freq = temp->frequency;
// 还要判断有没有这个频率的桶存在
if (temp->next->frequency != freq + 1)
{
Bucket* newbucket = new Bucket(freq + 1, key);
insert_bucket(temp, newbucket);
}
else
{
temp->next->bucket.insert(key);
}
map[key] = temp->next;
temp->bucket.erase(key);
if (temp->bucket.empty()) remove_bucket(temp);
}
}
void delete_bucket(string key)
{
if (map.find(key) == map.end())
{
cout << "error" << endl;
return;
}
Bucket* get = map.find(key)->second;
if (get->frequency == 1)
{
map.erase(key);
get->bucket.erase(key);
if (get->bucket.empty()) remove_bucket(get);
return;
}
if (get->last->frequency == get->frequency - 1)
{
get->last->bucket.insert(key);
}
else
{
Bucket* temp = new Bucket(get->frequency - 1,key);
insert_bucket(get->last, temp);
}
get->bucket.erase(key);
if (get->bucket.empty()) remove_bucket(get);
}
string get_max_freq()
{
return *tail->last->bucket.begin();
}
string get_min_freq()
{
return *head->next->bucket.begin();
}
};
int main()
{
AllOne allone;
string arr[] = { "I","love","you","the","world","I","I",
"love","I","love" };
int len = sizeof(arr) / sizeof(string);
for (int i = 0; i < len; i++)
{
allone.insert(arr[i]);
}
cout << allone.get_max_freq() << endl;
cout << allone.get_min_freq() << endl;
return 0;
}这应该是我目前为止写过最多行的代码