关注作者了解更多
我的其他CSDN专栏
关注作者了解更多
资料来源于网络,如有侵权请联系编者
目录
[实验一 离散时间信号与系统的时域分析](#实验一 离散时间信号与系统的时域分析)
[实验二 离散信号 Z 变换](#实验二 离散信号 Z 变换)
[实验三 IIR 滤波器的设计与信号滤波](#实验三 IIR 滤波器的设计与信号滤波)
[实验四 用窗函数法设计 FIR 数字滤波器](#实验四 用窗函数法设计 FIR 数字滤波器)
[实验五 用 FFT 作谱分析](#实验五 用 FFT 作谱分析)
[实验 6 综合实验](#实验 6 综合实验)
[2、实验内容 (三选一)](#2、实验内容 (三选一))
实验一 离散时间信号与系统的时域分析 1
实验二离散信号 Z 变换 7
实验三 双线性变换法设计 IIR 数字滤波器 19
实验四用窗函数法设计 FIR 数字滤波器 19
实验五用 FFT 作谱分析 19
实验六综合实验 25
实验一 离散时间信号与系统的时域分析
一、实验目的
-
1.掌握离散时间信号与系统的时域分析方法。
2.掌握序列傅氏变换的计算机实现方法,利用序列的傅氏变换对离散信号、系统及系 统响应进行频域分析。
3.熟悉理想采样的性质,了解信号采样前后的频谱变化,加深对采样定理的理解。
二、实验原理
实现2.离散时间系统的单位脉冲响应3连续时间信号的采样,绘制单位脉冲序列,绘制单位阶跃序列,绘制理想采样序列,绘制正弦序列,分析特性
三、实验过程记录
- 1单位脉冲序列
clear all;
clc;
n1=-5;n2=5;n0=0;
n=n1:n2;%自变量
x=[n==n0];%因变量,利用大括号判断里面的表达式是否成立,如果成立则函数有效,有数值
%否侧函数无效,没有数值
stem(n,x,'filled');%利用filled绘制实心火柴梗
axis([n1,n2,0,1.1*max(x)]);%绘制坐标系
xlabel('(n)');ylabel('幅度x(n)');
title('单位脉冲序列');
2单位冲激序列
clear all
n = 40;
x = ones(1,n);
xn = 0:n-1;
subplot(211);
stem(xn,x);
grid on
axis([-1 51 0 1.1]);
title('单位阶跃序列u(n)')
ylabel('u(n)');
xlabel('n');
x = [zeros(1,10),1,ones(1,29)];
subplot(212);
stem(xn,x);
grid on
axis([-1 51 0 1.1]);
title('单位跃迁序列u(n-10)')
ylabel('u(n-10)');
xlabel('n');
3正弦序列
clear all
n = 0:59;
x = sin(pi/7*n);
stem(n,x);
ylabel('x(n)');
xlabel('n');
title('正弦序列')
axis([0 40 -1.5 1.5]);
grid on;
4 理想采样序列
%绘制理想采样信号序列
%给定信号参数
A = 200;
alpha = 50*pi;
T = 1/10000;
Omega = 260*pi;
n = 0:1:100;
%计算信号在不同时刻的值
x = A.*exp(-alpha.*n.*T).*cos(Omega.*T.*n);
figure %绘制理想采样信号序列
stem(x,'g') %绘制单位抽样序列
%修改时间坐标值,保证信号0时刻的值为1,添加图的坐标含义标题等信息
set(gca, 'XTick', 1:101);
set(gca,'XTickLabel',0:100);
title('(d) Desired sampled signal')
grid on
xlabel('Time index n')
ylabel('Amplitude')
axis([1 101 -200 200]) %规范坐标轴范围
hold on
%给定信号参数
A = 100;
alpha = 0.4;
T = 1/1000;
Omega = 700*pi;
n = 0:100;
%计算信号在不同时刻的值
xx = A.*exp(-alpha.*n.*T).*cos(Omega.*T.*n);
%绘制修改参数后的理想采样信号序列
stem(xx,'b') %绘制单位抽样序列
改变参数A=1,a =0.4, W =700p ,产生理想采样信号序列 x n( ) 。
代码:
%给定信号参数
A = 1;
alpha = 0.4;
T = 1/10000;
Omega = 700*pi;
n = 0:1:100;
%计算信号在不同时刻的值
x = A.*exp(-alpha.*n.*T).*cos(Omega.*T.*n);
figure %绘制理想采样信号序列
stem(x,'g') %绘制单位抽样序列
%修改时间坐标值,保证信号0时刻的值为1,添加图的坐标含义标题等信息
set(gca, 'XTick', 1:101);
set(gca,'XTickLabel',0:100);
title('(d) Desired sampled signal')
grid on
xlabel('Time index n')
ylabel('Amplitude')
axis([1 101 -200 200]) %规范坐标轴范围
hold on
%给定信号参数
A = 100;
alpha = 0.4;
T = 1/1000;
Omega = 700*pi;
n = 0:100;
%计算信号在不同时刻的值
xx = A.*exp(-alpha.*n.*T).*cos(Omega.*T.*n);
%绘制修改参数后的理想采样信号序列
stem(xx,'b') %绘制单位抽样序列
>>结果截图
5. 实指数序列
clear all
n = 0:20;
x1 = 1.3.^n;
x2 = (-1.3).^n;
x3 = 0.8.^n;
x4 = (-0.8).^n;
subplot(221)
stem(n,x1,'fill')
grid on;
ylabel('x1(n)');
xlabel('n');
title('x1 = 1.6^n')
subplot(222)
stem(n,x2,'fill')
grid on;
ylabel('x2(n)');
xlabel('n');
title('x2 = (-1.6)^n')
subplot(223)
stem(n,x3,'fill')
grid on;
ylabel('x3(n)');
xlabel('n');
title('x1 = 0.8^n')
subplot(224)
stem(n,x4,'fill')
grid on;
ylabel('x4(n)');
xlabel('n');
title('x1 = 1(-0.8)^n')
四、结果分析
分别绘制了单位脉冲序列,单位阶跃序列,正弦序列,理想采样的指数正弦序列,改变参数后的理想采样正弦序列,实指数序列等图像
实验二 离散信号 Z 变换
一、实验目的
1、熟悉离散信号 Z 变换的原理及性质
2、熟悉常见信号的 Z 变换
3、了解正/反 Z 变换的 MATLAB 实现方法
4、了解离散信号的 Z 变换与其对应的理想抽样信号的傅氏变换和拉氏变换之间的关系
5、了解利用 MATLAB 实现离散系统的频率特性分析的方法
二、实验原理

实验过程记录
一、正 / 反 Z 变换

代码:
clc;
clear;
close all;
%%
% Example 1 for the Z transform
syms n % Define the temporal independent variable represented by the mathmatical symbols.
f = 0.5^n; % Define the sequence in the time domain.
Fz = ztrans(f); % Perform z transform based on the function ztrans.
disp(Fz); % Print the output.
%%
% Example 2 for the Z transform
syms z % Define the independent variable in the complex frequency domain.
Fz = 2*z/(2*z - 1); % Define the z transform in the complex frequency domain.
f = iztrans(Fz); % Perform inverse z transform based on the function iztrans.
disp(f); % Print the output
%%
% Example 3 for the Z transform
syms n % Define the independent variable
hn = kroneckerDelta(n, 1) + kroneckerDelta(n, 2) + kroneckerDelta(n,3); %Define the sequence in the time domain
disp(hn)
Hz = ztrans(hn); % Perform the z transform
disp(Hz)
Hz = simplify(Hz); % Simplify the expression of the H(z)
disp(Hz)运行结果:
z/(z - 1/2)
(1/2)^n
kroneckerDelta(n - 1, 0) + kroneckerDelta(n - 2, 0) + kroneckerDelta(n - 3, 0)
1/z + 1/z^2 + 1/z^3
(z^2 + z + 1)/z^3
三、离散系统的频率特性
-

-

-
代码:
%Example 4
a = [1,0]; % Define the coefficients of the denominator polynomial
b = [1,-0.5]; % Define the coefficients of the numerator polynomial
[H,omega] = freqz(b,a,10); % Compute the frequency response of the transfer function
disp(H)
disp(omega)
%%
%Example 5
a = [1,0]; % Define the coefficients of the denominator polynomial
b = [1,-0.5]; % Define the coefficients of the numerator polynomial
[H,omega] = freqz(b,a,200,'whole'); % Compute the frequency response of the transfer function
disp(H)
disp(omega)
Ha = abs(H); % Amplitude
Ph = angle(H); % Phase
运行结果:


求点代码如上
绘图代码
figure
subplot(2,1,1)
plot(omega,Ha)
hold on
set(gca, 'XTick', 0:pi/10:2*pi);
set(gca,'XTickLabel',0:pi/10:2*pi);
title('(a) Amplitude-frequency response')
grid on
xlabel('omega')
ylabel('Amplitude')
axis([0 2*pi 0.5 1.5])
grid on
subplot(2,1,2)
plot(omega,Ph)
set(gca, 'XTick', 0:pi/10:2*pi);
set(gca,'XTickLabel',0:pi/10:2*pi);
title('(a) Phase-frequency response')
grid on
xlabel('omega')
ylabel('Phase')
axis([0 2*pi -0.6 0.6])
grid on运行结果


三、实验内容

代码:
syms z; % Define the independent variable
F1z = (z^2+z+1)/(z^2+z-2);
f1 = iztrans(F1z); % Perform the inverse z transform
disp(f1)运行结果:
(-2)^n/2 - kroneckerDelta(n, 0)/2 + 1

题目二
代码:
syms z;Flz=(z^4+z^3+z^2+z+1)/(z^4);fl=iztrans(Flz);disp(fl)结果:
kroneckerDelta(n - 1, 0) + kroneckerDelta(n - 2, 0) + kroneckerDelta(n - 3, 0) + kroneckerDelta(n - 4, 0) + kroneckerDelta(n, 0)

题目三;
代码
syms z;Flz=(2*z^2+6*z+12)/(z^4);fl=iztrans(Flz);disp(fl)结果:
2*kroneckerDelta(n - 2, 0) + 6*kroneckerDelta(n - 3, 0) + 12*kroneckerDelta(n - 4, 0)5. 实验要求

六.实验感想
通过Z变换和Z反变换,熟悉了MATLAB的使用
实验三 IIR 滤波器的设计与信号滤波
1、实验目的
(1)熟悉用双线性变换法设计 IIR 数字滤波器的原理与方法。
(2)掌握数字滤波器的计算机仿真方法。
(3)通过观察对实际心电图信号的滤波作用,获得数字滤波的感性知识
2 . 实验原理

3、实验步骤及内容

实验代码
用双线性变换法设计Butterworth低通数字滤波器,要求通带频率为 ,通带波纹小于1dB,阻带频率为 ,幅度衰减大于15dB,采样频率为Fs=100Hz。
clc;
%写出已知条件,设置采样点数
wp=0.25*pi;ws=0.4*pi;
rp=1;as=15;
fs=2000;Nn=128;
%由数字指标映射到模拟滤波器指标
WP=wp*fs;WS=ws*fs;
%利用巴特沃斯滤波器的设计方法,设计一个模拟滤波器
[N,Wn]=buttord(WP,WS,rp,as,'s');
[z,p,k]=buttap(N);
[B,A]=zp2tf(z,p,k);
%转换到数字滤波器
[b,a]=lp2lp(B,A,Wn);%从一个低通原型变换为具有不同截止频率的低通滤波器
[bz,az]=impinvar(b,a,fs);%根据冲激响应不变法得到数字滤波器
freqz(bz,az,Nn,fs);
WS=2*fs*tan(ws/2);
WP=2*fs*tan(wp/2);
[bz,az]=bilinear(b,a,fs);
freqz(bz,az,Nn,fs);
[H,w]=freqz(bz,az);
figure;
subplot(211);
plot(w/pi,abs(H));
subplot(212);
plot(w/pi,angle(H));运行结果


6 实验报告要求

7实验感想
通过IIR滤波器的设计,熟悉了MATLAB的使用
实验四 用窗函数法设计 FIR 数字滤波器
1、实验目的
(1)掌握用窗函数法设计 FIR 数字滤波器的原理和方法。
(2)熟悉线性相位 FIR 数字滤波器特性。
(3)了解各种窗函数对滤波特性的影响
2、实验原理
 、
、

3、实验步骤及内容

实验代码:
1 设计滤波器,采用汉明窗,长度41(阶数40),采样频率2000hz:
clear all; close all; clc;
% 滤波器长度
N=41;
%采样频率
fs=2000;
%各种滤波器的特征频率
fc_lpf=200;
fc_hpf=200;
fp_bandpass=[200 400];
fc_stop=[200 400];
%以采样频率的一般,对频率归一化
wn_lpf=fc_lpf*2/fs;
wn_hpf=fc_hpf*2/fs;
wn_bandpass=fp_bandpass*2/fs;
wn_stop=fc_stop*2/fs;
%采用fir1函数设计FIR滤波器
b_lpf=fir1(N-1,wn_lpf);
b_hpf=fir1(N-1,wn_hpf,'high');
b_bandpass=fir1(N-1,wn_bandpass,'bandpass');
b_stop=fir1(N-1,wn_stop,'stop');
%求幅频响应
m_lpf=20*log(abs(fft(b_lpf)))/log(10);
m_hpf=20*log(abs(fft(b_hpf)))/log(10);
m_bandpass=20*log(abs(fft(b_bandpass)))/log(10);
m_stop=20*log(abs(fft(b_stop)))/log(10);
% 设置频率响应的横坐标单位为hz
x_f=0:(fs/length(m_lpf)):fs/2;
% 单位脉冲响应
subplot(4,2,1);stem(b_lpf);xlabel('n');ylabel('h(n)');legend('lpf');
subplot(4,2,3);stem(b_hpf);xlabel('n');ylabel('h(n)');legend('hpf');
subplot(4,2,5);stem(b_bandpass);xlabel('n');ylabel('h(n)');legend('bandpass');
subplot(4,2,7);stem(b_stop);xlabel('n');ylabel('h(n)');legend('stop');
% 幅频响应
subplot(4,2,2);plot(x_f,m_lpf(1:length(x_f)));xlabel('频率(hz)');ylabel('幅度(db)','fontsize',8);legend('lpf')
subplot(4,2,4);plot(x_f,m_hpf(1:length(x_f)));xlabel('频率(hz)');ylabel('幅度(db)','fontsize',8);legend('hpf')
subplot(4,2,6);plot(x_f,m_bandpass(1:length(x_f)));xlabel('频率(hz)');ylabel('幅度(db)','fontsize',8);legend('bandpass')
subplot(4,2,8);plot(x_f,m_stop(1:length(x_f)));xlabel('频率(hz)');ylabel('幅度(db)','fontsize',8);legend('stop');仿真脉冲响应和幅频响应图

6 实验要求

7 . 实验感想
通过FIR滤波器设计,熟悉了MATLAB的使用
实验五 用 FFT 作谱分析
1 实验目的
(1)进一步加深 DFT 算法原理和基本性质的理解(因为 FFT 只是 DFT 的一种快速算法,所 以 FFT 的运算结果必然满足 DFT 的性质)
(2)熟悉 FFT 算法原理及子程序的应用。
(3)掌握用 FFT 对连续信号和时域离散信号进行频谱分析的基本方法。了解可能出现的分 析误差和原因,以便在实际中正确应用 FFT。
2、实验原理

3、实验步骤及内容


实验数据记录
%《数字信号处理(第4版)》第10章实验2程序exp2a.m
% 西安电子科技大学出版社出版 高西全 丁玉美 合著 2016年
% 时域采样理论验证
Tp=64/1000;
%产生M长采样序列x(n)
% Fs=1000;T=1/Fs;
Fs=1000;T=1/Fs;
M=Tp*Fs;n=0:M-1;
A=444.128;alph=pi*50*2^0.5;omega=pi*50*2^0.5;
xnt=A*exp(-alph*n*T).*sin(omega*n*T);
Xk=T*fft(xnt,M); %M点FFT[xnt)]
yn='xa(nT)';
subplot(3,2,1);tstem(xnt,yn);box on;title('(a) Fs=1000Hz');
k=0:M-1;fk=k/Tp;
subplot(3,2,2);plot(fk,abs(Xk));title('(a) T*FT[xa(nT)],Fs=1000Hz');
xlabel('f(Hz)');
ylabel('幅度');axis([0,Fs,0,1.2*max(abs(Xk))])
% Fs=300;T=1/Fs;
Fs=300;T=1/Fs;
M=ceil(Tp*Fs);n=0:M-1;
xnt=A*exp(-alph*n*T).*sin(omega*n*T);
Xk=T*fft(xnt,M); %M点FFT[xnt)]
yn='xa(nT)';
subplot(3,2,3);tstem(xnt,yn);box on;title('(b) Fs=300Hz');
k=0:M-1;fk=k/Tp;
subplot(3,2,4);plot(fk,abs(Xk));title('(b) T*FT[xa(nT),Fs=300Hz');
xlabel('f(Hz)');ylabel('幅度');axis([0,Fs,0,1.2*max(abs(Xk))])
% Fs=200;T=1/Fs;
Fs=200;T=1/Fs;
M=ceil(Tp*Fs);n=0:M-1;
xnt=A*exp(-alph*n*T).*sin(omega*n*T);
Xk=T*fft(xnt,M); %M点FFT[xnt)]
yn='xa(nT)';subplot(3,2,5);tstem(xnt,yn);box on;title('(c) Fs=200Hz');
k=0:M-1;fk=k/Tp;
subplot(3,2,6);plot(fk,abs(Xk));title('(c) T*FT[xa(nT),Fs=200Hz');
xlabel('f(Hz)');ylabel('幅度');axis([0,Fs,0,1.2*max(abs(Xk))])先对下列序列进行谱分析,

选择FFT的变换区间N为8和16两种情况进行频谱分析。分别打印其幅频特性曲线,并进行对比、分析和讨论。
对于第一个序列

对于第2个序列

对于第3个序列

对下列周期序列进行频谱分析:

选择FFT的变换区间N为8和16两种情况分别对以上序列进行频谱分析。分别打印其幅频特性曲线,并进行对比、分析和讨论。
对于第4个序列

对于第5个序列

对模拟周期信号进行频谱分析:

选择采样率Fs=64Hz,对变换区间N=16,32,64三种情况进行谱分析。分别打印其幅频特性,并进行分析和讨论。
对于第6个序列

6 实验报告要求

内容总结
图1a和1b说明x1(n)=R4(n)的8点DFT和16点DFT分别是x1(n)的频谱函数的8点采样和16点采样,图2a和图3a表明x3(n)=x2(n+3)8R8(n)的8点DFT的模相等,但是当N=16时,x3(n)与x2(n)不满足位移关系,所以导致2b和3b的模不相同。
x4(n)的周期为8,所以N=8和N=16是其周期的整数倍,得到正确的单一频率正弦波的频谱,仅在0.25Π处有1跟单一谱线,如图4a和4b所示。
X5(n)的周期为16,所以N=8时,得到的频谱不正确,如5a所示。当N=16时,为其周期的整数倍,故能得到正确的频谱,在0.25Π和0.125Π处有两根单一谱线,如图5b所示。
x6(n)有三个频率成分,f1=4hz,f2=8hz,f3=10hz。所以x6(n)的周期为0.5,采样频率Fs=64Hz = 16f1 = 8f2 = 6.4f3。变换区间N=16时,观察时间Tp = 16T = 0.25s,不是x6(t)的整数倍周期,所以所得频谱不正确,如图6a所示。变换区间N=32,64时,观察时间Tp=0.5s,1s,是x6(t)的整数周期,所以所得频谱正确,如图6b和6c所示。图中3根谱线正好位于4Hz,8Hz,10Hz处。变换区间N=64时频谱幅度是变换区间N=32时2倍.
通过以上实验进一步论证了当周期信号的频谱是离散谱,只有用整数倍周期的长度做FFT,得到的离散谱才能代表周期信号的频谱。
实验 6 综合实验
1 实验目的
(1)了解语音信号的获取及基本处理
(2)给定设计指标,能选用多种方法设计出符合指标要求的滤波器。
(3)掌握各种设计方法的原理,步骤以及特点。
(4)培养学生实际应用及综合设计的能力。
2、实验内容 (三选一)

二.设计一个数字带通滤波器
采用F IR 函数设计滤波器
clear all; close all; clc;
% 滤波器长度
N=41;
%采样频率
fs=2000;
%各种滤波器的特征频率
fc_lpf=200;
fc_hpf=200;
fp_bandpass=[200 400];
fc_stop=[200 400];
%以采样频率的一般,对频率归一化
wn_lpf=fc_lpf*2/fs;
wn_hpf=fc_hpf*2/fs;
wn_bandpass=fp_bandpass*2/fs;
wn_stop=fc_stop*2/fs;
%采用fir1函数设计FIR滤波器
b_lpf=fir1(N-1,wn_lpf);
b_hpf=fir1(N-1,wn_hpf,'high');
b_bandpass=fir1(N-1,wn_bandpass,'bandpass');
b_stop=fir1(N-1,wn_stop,'stop');
%求幅频响应
m_lpf=20*log(abs(fft(b_lpf)))/log(10);
m_hpf=20*log(abs(fft(b_hpf)))/log(10);
m_bandpass=20*log(abs(fft(b_bandpass)))/log(10);
m_stop=20*log(abs(fft(b_stop)))/log(10);
% 设置频率响应的横坐标单位为hz
x_f=0:(fs/length(m_lpf)):fs/2;
% 单位脉冲响应
subplot(4,2,1);stem(b_lpf);xlabel('n');ylabel('h(n)');legend('lpf');
subplot(4,2,3);stem(b_hpf);xlabel('n');ylabel('h(n)');legend('hpf');
subplot(4,2,5);stem(b_bandpass);xlabel('n');ylabel('h(n)');legend('bandpass');
subplot(4,2,7);stem(b_stop);xlabel('n');ylabel('h(n)');legend('stop');
% 幅频响应
subplot(4,2,2);plot(x_f,m_lpf(1:length(x_f)));xlabel('频率(hz)');ylabel('幅度(db)','fontsize',8);legend('lpf')
subplot(4,2,4);plot(x_f,m_hpf(1:length(x_f)));xlabel('频率(hz)');ylabel('幅度(db)','fontsize',8);legend('hpf')
subplot(4,2,6);plot(x_f,m_bandpass(1:length(x_f)));xlabel('频率(hz)');ylabel('幅度(db)','fontsize',8);legend('bandpass')
subplot(4,2,8);plot(x_f,m_stop(1:length(x_f)));xlabel('频率(hz)');ylabel('幅度(db)','fontsize',8);legend('stop');脉冲仿真响应和幅频响应图

设计带通滤波器

% 定义截止频率和阻尼比
omega_0 = 10;
xi = 0.707;
% 创建二阶低通滤波器传递函数模型
H_second_order_lowpass = tf(omega_0^2, [1, 2*xi*omega_0, omega_0^2]);
% 创建二阶高通滤波器传递函数模型
H_second_order_highpass = tf([1, 0, 0], [1, 2*xi*omega_0, omega_0^2]);
% 创建二阶带通滤波器传递函数模型
H_second_order_bandpass = tf([2*xi*omega_0, 0], [1, 2*xi*omega_0, omega_0^2]);
% 创建二阶带阻滤波器传递函数模型
H_second_order_bandstop = tf([1, 0, omega_0^2], [1, 2*xi*omega_0, omega_0^2]);
% 创建第一个图:对比二阶低通和高通滤波器的频率响应曲线
figure;
subplot(1,2,1);
bode(H_second_order_lowpass, 'b', H_second_order_highpass, 'r');
grid on;
legend('Lowpass', 'Highpass');
title('二阶滤波器:低通、高通');
% 创建第二个图:对比二阶带通和带阻滤波器的频率响应曲线
subplot(1,2,2);
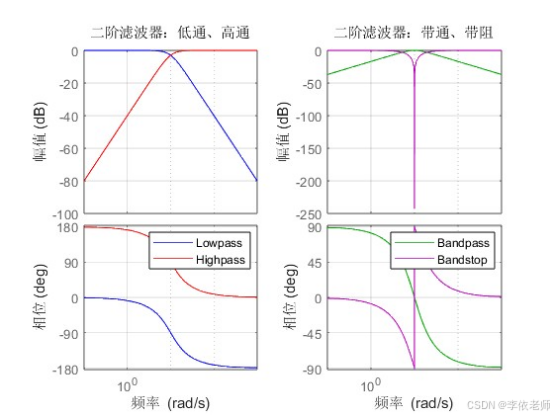
bode(H_second_order_bandpass, 'g', H_second_order_bandstop, 'm');
grid on;
legend('Bandpass', 'Bandstop');
title('二阶滤波器:带通、带阻');仿真曲线:
3实验报告要求
(1)简述实验目的。
(2)编程实现各实验内容,列出实验清单及说明。
(3)总结实验结论并写出实验收获或感想
4 . 实验感想
掌握了低通,高通,带通滤波器的基本设计思想,熟悉了MATLAB的使用。