[优选算法专题八.分治-归并 ——NO.49 翻转对]

题目链接

493. 翻转对

题目描述

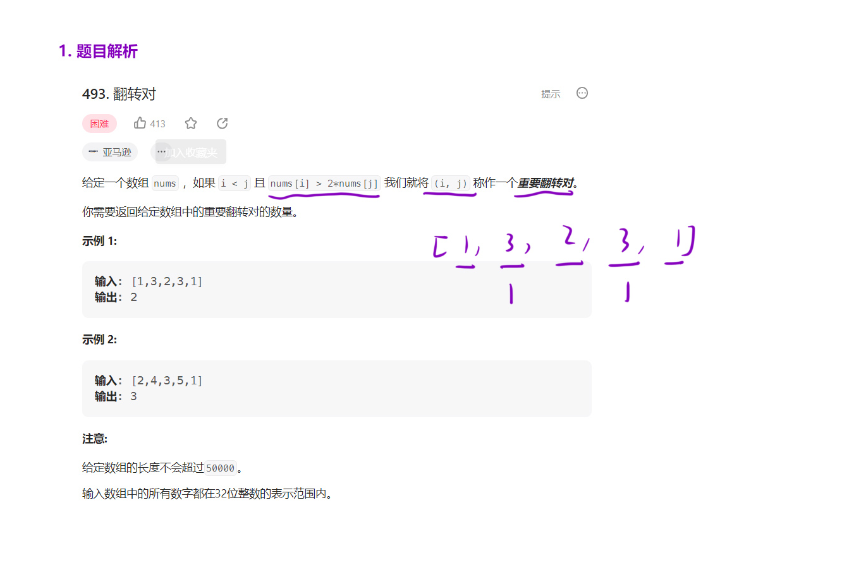
题目解析

总体功能概述

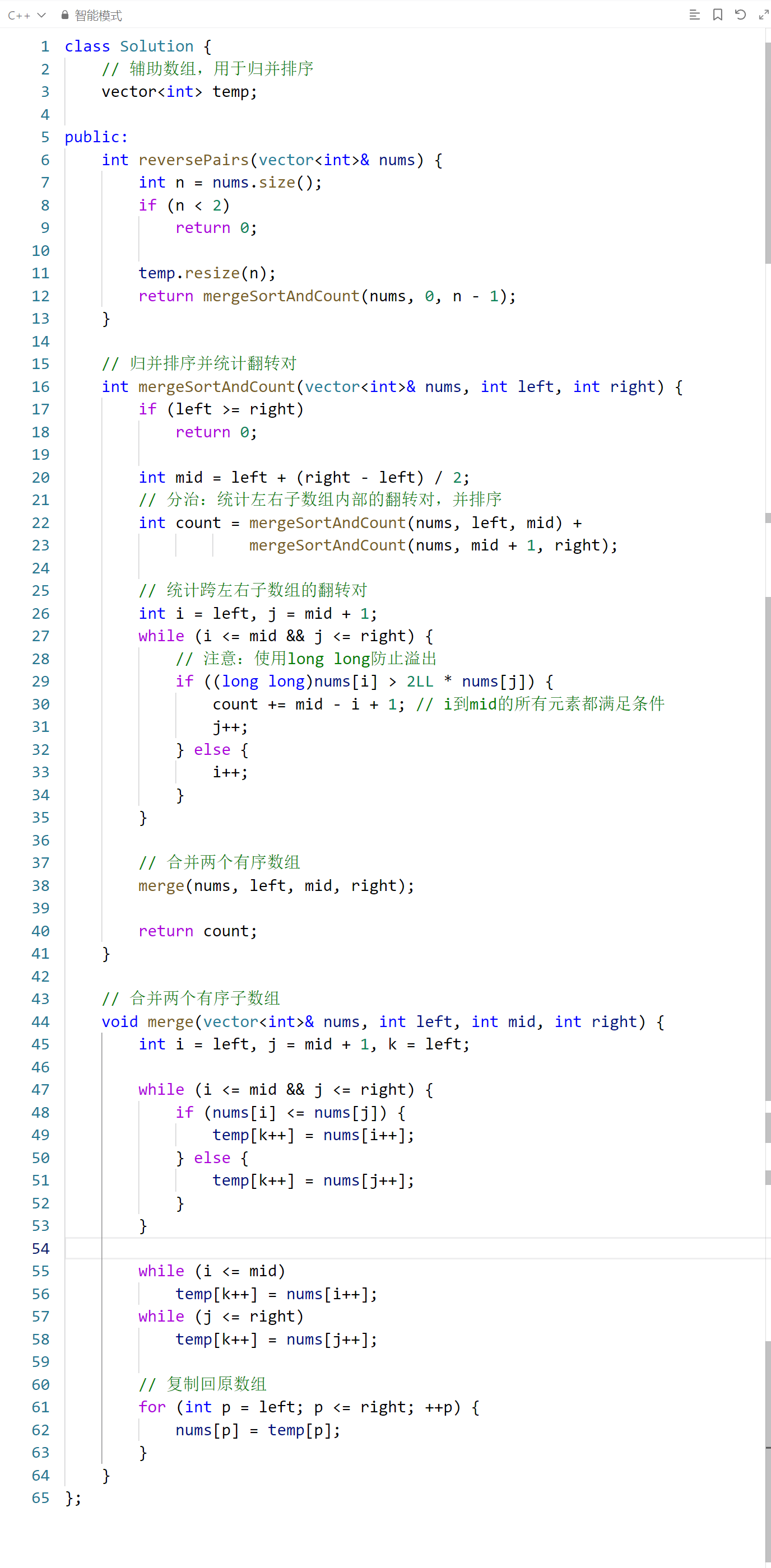
代码通过归并排序将数组不断二分，在合并阶段统计三类翻转对：左子数组内部的、右子数组内部的、跨左右子数组的，最终返回总数。时间复杂度为 O (n log n) ，空间复杂度为 O (n)。

逐段逻辑解析

1. 主函数 reversePairs

int reversePairs(vector<int>& nums) {
    int n = nums.size();
    if (n < 2)
        return 0;

    temp.resize(n);
    return mergeSortAndCount(nums, 0, n - 1);
}

• 处理边界情况：数组长度小于 2 时，直接返回 0（无翻转对）。
• 初始化辅助数组temp，调用核心函数mergeSortAndCount开始分治统计。

2. 核心分治函数 mergeSortAndCount

int mergeSortAndCount(vector<int>& nums, int left, int right) {
    if (left >= right)
        return 0;

    int mid = left + (right - left) / 2;
    // 分治：统计左右子数组内部的翻转对，并排序
    int count = mergeSortAndCount(nums, left, mid) +
                mergeSortAndCount(nums, mid + 1, right);

    // 统计跨左右子数组的翻转对
    int i = left, j = mid + 1;
    while (i <= mid && j <= right) {
        if ((long long)nums[i] > 2LL * nums[j]) {
            count += mid - i + 1; // i到mid的所有元素都满足条件
            j++;
        } else {
            i++;
        }
    }

    // 合并两个有序数组
    merge(nums, left, mid, right);

    return count;
}

• 递归终止条件：子数组长度为 1 时，返回 0（无翻转对）。
• 分治统计：递归统计左、右子数组的翻转对数量并求和。
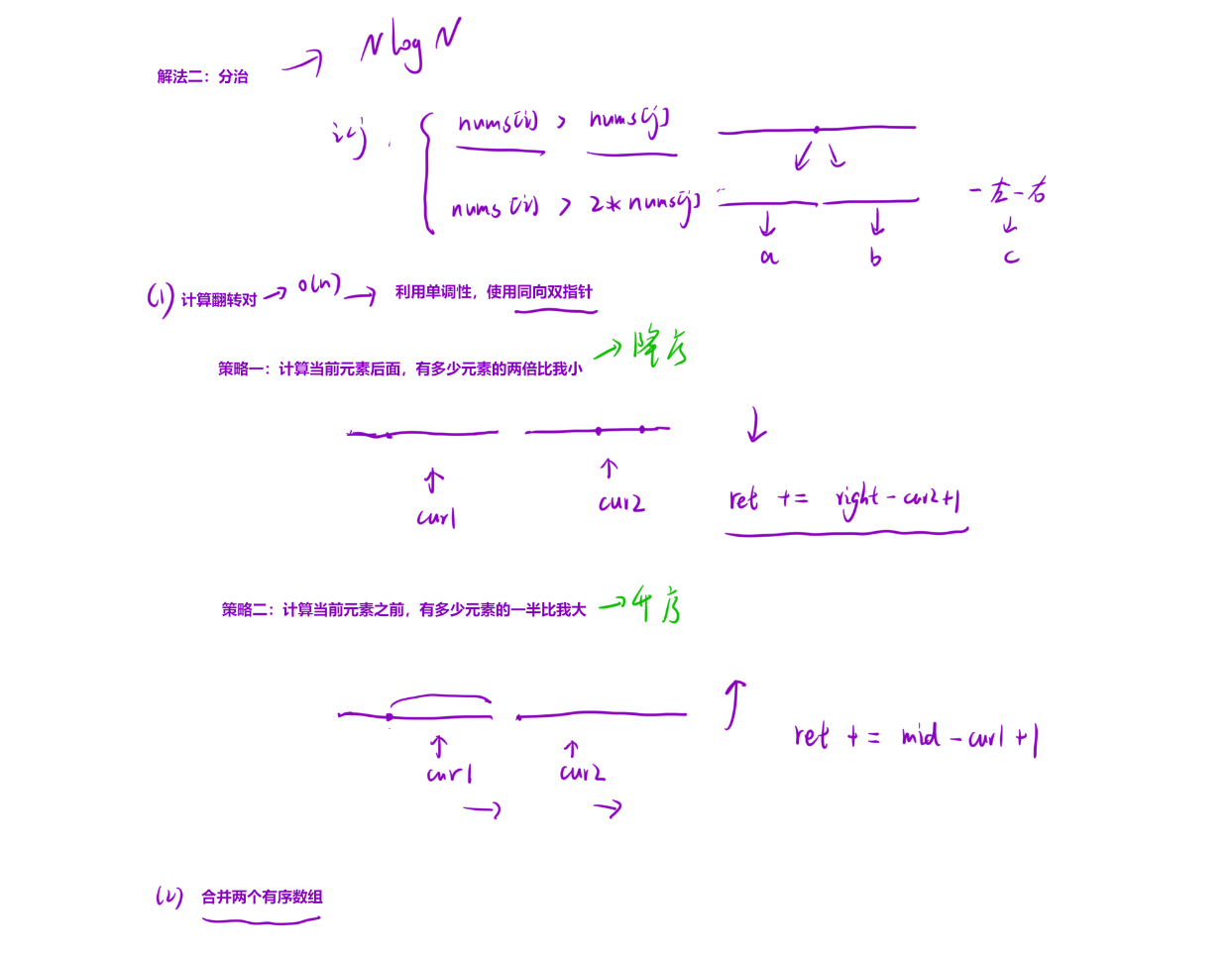
• 跨数组统计 ：利用双指针法高效统计跨左右子数组的翻转对：
  • 若nums[i] > 2*nums[j]，则左子数组中i到mid的所有元素都满足条件（因左子数组有序），直接累加mid - i + 1，并移动j。
  • 否则移动i，继续检查。
• 合并数组 ：调用merge函数将左右子数组合并为有序数组，为上层统计做准备。

3. 合并函数 merge

void merge(vector<int>& nums, int left, int mid, int right) {
    int i = left, j = mid + 1, k = left;

    while (i <= mid && j <= right) {
        if (nums[i] <= nums[j]) {
            temp[k++] = nums[i++];
        } else {
            temp[k++] = nums[j++];
        }
    }

    while (i <= mid)
        temp[k++] = nums[i++];
    while (j <= right)
        temp[k++] = nums[j++];

    // 复制回原数组
    for (int p = left; p <= right; ++p) {
        nums[p] = temp[p];
    }
}

• 标准归并排序的合并逻辑：用双指针遍历左右子数组，将较小元素依次放入temp。
• 处理剩余元素：将左 / 右子数组中未处理完的元素直接追加到temp。
• 复制回原数组：将temp中有序的结果覆盖原数组对应区间，保证子数组有序。

输入与输出分析

• 输入 ：整数数组nums，如[1,3,2,3,1]。
• 输出 ：重要翻转对的数量，如输入[1,3,2,3,1]时输出2（对应数对(3,1)和(3,1)）。

使用与扩展指南

• 直接调用reversePairs函数即可得到结果，无需额外操作。
• 若需统计其他条件的逆序对（如nums[i] > nums[j]），只需修改跨数组统计的判断条件（如去掉2*）。

总结

• 核心思想：归并排序的分治特性，将统计翻转对的问题分解为子问题，利用有序子数组的特性高效统计。
• 关键优化：双指针法线性统计跨数组翻转对，避免暴力枚举的 O (n²) 复杂度。
• 注意点 ：使用long long防止2*nums[j]溢出，确保判断条件准确。