目录
引例
画图分析:

使用动态规划解决
原理:能够将所有子串是否是回文的信息保存在dp表中
在使用暴力方法枚举出所有子串,是使用两指针(i,j)依次往后枚举的,且满足i<=j
所以需要建立二维的dp表,在填表时只需填上三角位置即可
1.状态表示:
dp[i][j]表示字符串s的[i,j](i是起始位置,j是结束位置)的这个子串是否是回文
2.状态转移方程

对于线性dp可以采用多画图的方式来分析

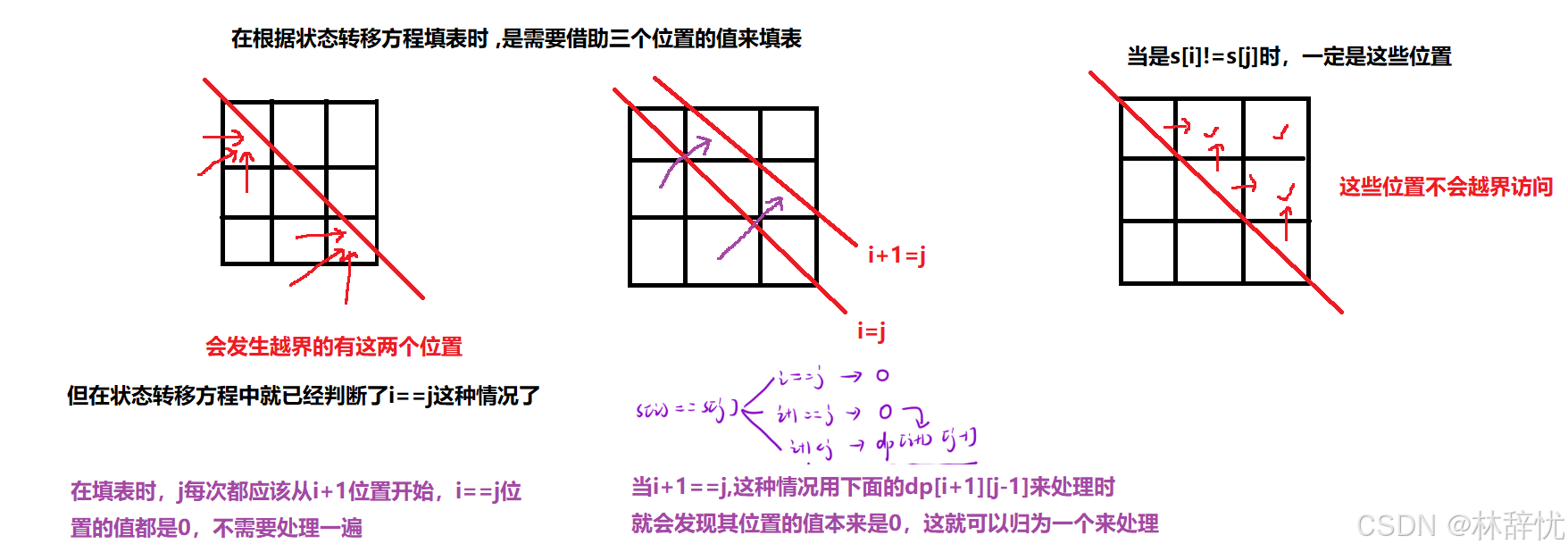
3.初始化
因为满足i<=j 并且越界的情况都已经被判断了,是无需做初始化的
4.填表顺序
因为在求dp[i][j]时会用到dp[i+1][j-1]的值,所以填表顺序是整体从下往上,每一行从左往右
5.返回值
返回dp表中true的数量
具体代码
cpp
int countSubstrings(string s)
{
int n=s.size();
vector<vector<bool>> dp(n,vector<bool>(n));//创建dp表
int ret=0;
for(int i=n-1;i>=0;--i)//填表
{
for(int j=i;j<n;++j)//从i位置开始往后枚举
{
if(s[i]==s[j])
{
dp[i][j]=i+1<j? dp[i+1][j-1]:true;
}
if(dp[i][j]) ++ret;
}
}
return ret;//返回
}其余经典OJ题
1.第一题
画图分析:

使用动态规划解决
对于本道题是计算最长的回文子串,在上面的例题中已经实现了判断字符串的子串是否是回文,只需在dp表中为true的位置找出最长的回文串
其余的参考上面的例题
5.返回值
在dp表中为true的位置找出最长回文串的起始位置i及长度,返回子串
具体代码:
cpp
string longestPalindrome(string s)
{
int n=s.size();
vector<vector<bool>> dp(n,vector<bool>(n));
int begin=0,len=1;
for(int i=n-1;i>=0;--i)
{
for(int j=i;j<n;++j)
{
if(s[i]==s[j])
{
dp[i][j]=i+1<j? dp[i+1][j-1]:true;
}
if(dp[i][j] && j-i+1>len)
{
begin=i;
len=j-i+1;
}
}
}
return s.substr(begin,len);
}2.第二题
画图分析:
 使用动态规划来解决
使用动态规划来解决
对于本题是将字符串划分为三子串,只要每个子串是回文串即可
这里可以两下标i,j来划分这个字符串

此时只需要根据上面例题所实现的dp表来逐步划分区间判断
具体代码:
cpp
bool checkPartitioning(string s)
{
int n=s.size();
//用dp把所有的子串是否是回文预处理一下
vector<vector<bool>> dp(n,vector<bool>(n));
for(int i=n-1;i>=0;--i)
{
for(int j=i;j<n;++j)
{
if(s[i]==s[j])
{
dp[i][j]=i+1<j? dp[i+1][j-1]:true;
}
}
}
//枚举所有的第二个子串的起始位置及结束位置
for(int i=1;i<n-1;++i)
{
for(int j=i;j<n-1;++j)
{
if(dp[0][i-1] && dp[i][j] && dp[j+1][n-1]) return true;
}
}
return false;
}3.第三题
画图分析:
 使用动态规划来解决
使用动态规划来解决
1.状态表示 ---经验+题目要求
dp[i]表示字符串s.substr(0,i+1)这个子串要分割为回文串的最少分割次数
2.状态转移方程

3.初始化
对于这里的dp表本身在填表时由于j>0是不会访问越界的,但题目求得是最小值
在求dp[i]=min(dp[j-1]+1,dp[i])时,若初始化时都0时,dp[i]=0,是会影响求min的,因此初始化为INT_MAX
4.填表顺序 ------从左往右
5.返回值-------dp[n-1]
具体代码:
cpp
int minCut(string s)
{
//预处理一下
int n=s.size();
vector<vector<bool>> IsPal(n,vector<bool>(n));
for(int i=n-1;i>=0;--i)
for(int j=i;j<n;++j)
if(s[i]==s[j])
IsPal[i][j]=i+1<j? IsPal[i+1][j-1]:true;
vector<int> dp(n,INT_MAX);
for(int i=0;i<n;++i)
{
if(IsPal[0][i]) dp[i]=0;
else
{
for(int j=1;j<=i;++j)
if(IsPal[j][i]) dp[i]=min(dp[j-1]+1,dp[i]);
}
}
return dp[n-1];
}4.第四题
画图分析:
 使用动态规划解决
使用动态规划解决
1.状态表示
dp[i]表示以i位置为结尾的所有子序列中,最长回文子序列的长度
当使用此状态表示来求解状态转移方程时
当求解dp[i]时,因为此题是子序列,所以需要用到dp[i-1],dp[i-2],....,而dp表中存的只是长度,当在每种结果后添加字符s[i]后,并不能保证是继续是回文串,因此推导不出状态转移方程
这时可以借用上面例题的方法来解决这题

状态表示:
dp[i][j]表示s字符串[i,j]区间内的所有子序列,最长回文子序列的长度
2.状态转移方程

3.初始化
对于本题可以不用初始化,会越界的位置为i==j,而这些位置已经判断过了

4.填表顺序
整体从上往下,每一行从左往右
5.返回值 dp[0][n-1]
具体代码:
cpp
int longestPalindromeSubseq(string s)
{
int n=s.size();
vector<vector<int>> dp(n,vector<int>(n));
for(int i=n-1;i>=0;--i)
{
for(int j=i;j<n;++j)
{
if(s[i]==s[j])
{
if(i==j) dp[i][j]=1;
else dp[i][j]=dp[i+1][j-1]+2;
}
else
dp[i][j]=max(dp[i+1][j],dp[i][j-1]);
}
}
return dp[0][n-1];
}5.第五题
OJ 传送门Leetcode<1312>让字符串成为回文串的最少插入次数
画图分析:
 使用动态规划解决
使用动态规划解决
1.状态表示 根据经验+题目要求
dp[i][j]表示:s字符串[i,j]区间的子串,让它变为回文串的最小操作次数
2.状态转移方程---认识根据s[i]与s[j]的关系来判断

3.初始化:
4.填表顺序
整体从下往上,每一行从左往右
5.返回值 dp[0][n-1]
具体代码:
cpp
int minInsertions(string s)
{
int n=s.size();
vector<vector<int>> dp(n,vector<int>(n));
for(int i=n-1;i>=0;--i)
{
for(int j=i+1;j<n;++j)
{
if(s[i]==s[j]) dp[i][j]=dp[i+1][j-1];
else dp[i][j]=min(dp[i][j-1],dp[i+1][j])+1;
}
}
return dp[0][n-1];
}