今天是动态规划的最后一篇内容了,本篇主要是针对回文字符串这种"与众不同"的递推规律来进行讲解
647. 回文子串
统计并返回这个字符串中 回文子串 的数目
暴力解法
两层for循环,遍历区间起始位置和终止位置,然后还需要一层遍历判断这个区间是不是回文。所以时间复杂度:O(n^3)
动态规划
- 确定dp数组(dp table)以及下标的含义
如果大家做了很多这种子序列相关的题目,在定义dp数组的时候 很自然就会想题目求什么,我们就如何定义dp数组。
绝大多数题目确实是这样,不过本题如果我们定义,dp[i] 为 下标i结尾的字符串有 dp[i]个回文串的话,我们会发现很难找到递归关系。dp[i] 和 dp[i-1] ,dp[i + 1] 看上去都没啥关系。所以我们要看回文串的性质。
我们在判断字符串S是否是回文,那么如果我们知道 s[1],s[2],s[3] 这个子串是回文的,那么只需要比较 s[0]和s[4]这两个元素是否相同,如果相同的话,这个字符串s 就是回文串。那么此时我们是不是能找到一种递归关系,也就是判断一个子字符串(字符串下标范围[i,j])是否回文,依赖于,子字符串(下标范围[i + 1, j - 1])) 是否是回文。
所以为了明确这种递归关系,我们的dp数组是要定义成二维dp数组。dp[i][j](布尔类型):表示区间范围[i,j] (注意是左闭右闭)的子串是否是回文子串,如果是dp[i][j]为true,否则为false。
- 确定递推公式(这个地方要和遍历顺序一起理解,递推公式对于解题非常重要)
在确定递推公式时,就要分析如下几种情况。整体上是两种,就是s[i]与s[j]相等,s[i]与s[j]不相等这两种。
当s[i]与s[j]不相等,那没啥好说的了,dp[i][j]一定是false。
当s[i]与s[j]相等时,这就复杂一些了,有如下三种情况
- 情况一:下标i 与 j相同,同一个字符例如a,当然是回文子串
- 情况二:下标i 与 j相差为1,例如aa,也是回文子串
- 情况三:下标:i 与 j相差大于1的时候,例如cabac,此时s[i]与s[j]已经相同了,我们看i到j区间是不是回文子串就看aba是不是回文就可以了,那么aba的区间就是 i+1 与 j-1区间,这个区间是不是回文就看dp[i + 1][j - 1]是否为true。
- dp数组如何初始化
dp[i][j]初始化为false。
- 确定遍历顺序
遍历顺序可就有点讲究了。
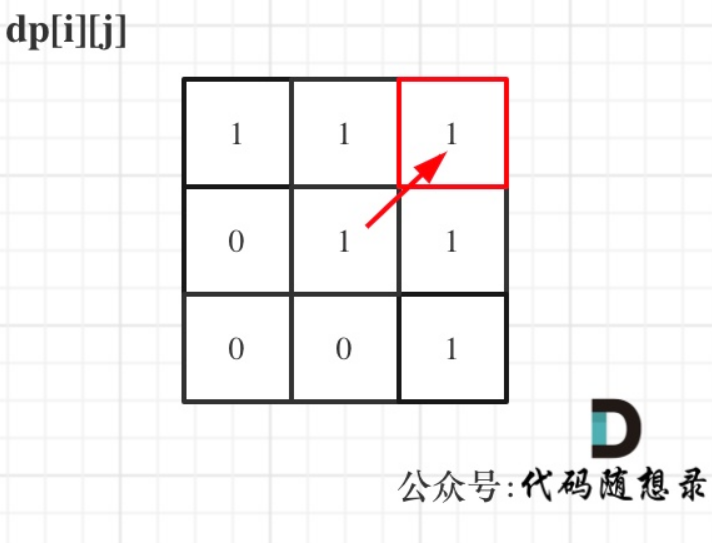
首先从递推公式中可以看出,情况三是根据dp[i + 1][j - 1]是否为true,在对dp[i][j]进行赋值true的。dp[i + 1][j - 1] 在 dp[i][j]的左下角所以一定要从下到上,从左到右遍历,这样保证dp[i + 1][j - 1]都是经过计算的。
总而言之,一个道理,都是为了保证dp[i + 1][j - 1]都是经过计算的。
- 举例推导dp数组
举例,输入:"aaa",dp[i][j]状态如下:
python
class Solution:
def countSubstrings(self, s: str) -> int:
dp = [[False] * len(s) for _ in range(len(s))]
result = 0
for i in range(len(s)-1, -1, -1): #注意遍历顺序
for j in range(i, len(s)):
if s[i] == s[j]:
if j - i <= 1: #情况一 和 情况二
result += 1
dp[i][j] = True
elif dp[i+1][j-1]: #情况三
result += 1
dp[i][j] = True
return result双指针法
回文子串的对称中心有两种情况:
- 奇数长度的回文子串(如 "aba"):中心是单个字符(示例中的 "b")。
- 偶数长度的回文子串(如 "abba"):中心是两个相邻字符(示例中的 "bb")。
中心扩展法的逻辑是:
- 枚举字符串中每个可能的中心(单个字符或相邻两个字符)。
- 从中心向两侧扩展,判断扩展后的子串是否为回文。
- 每扩展成功一次,就计数一个回文子串。
python
class Solution:
def countSubstrings(self, s: str) -> int:
result = 0
for i in range(len(s)):
result += self.extend(s, i, i, len(s)) #以i为中心
result += self.extend(s, i, i+1, len(s)) #以i和i+1为中心
return result
def extend(self, s, i, j, n):
res = 0
while i >= 0 and j < n and s[i] == s[j]:
i -= 1
j += 1
res += 1
return res516.最长回文子序列
这种回文子序列可以删除元素是很难想的,因为规律不是很直观。本题和上题的区别在于:回文子串是要连续的,回文子序列可不是连续的!
- 确定dp数组(dp table)以及下标的含义
dp[i][j]:字符串s在[i, j]范围内最长的回文子序列的长度为dp[i][j]。
- 确定递推公式
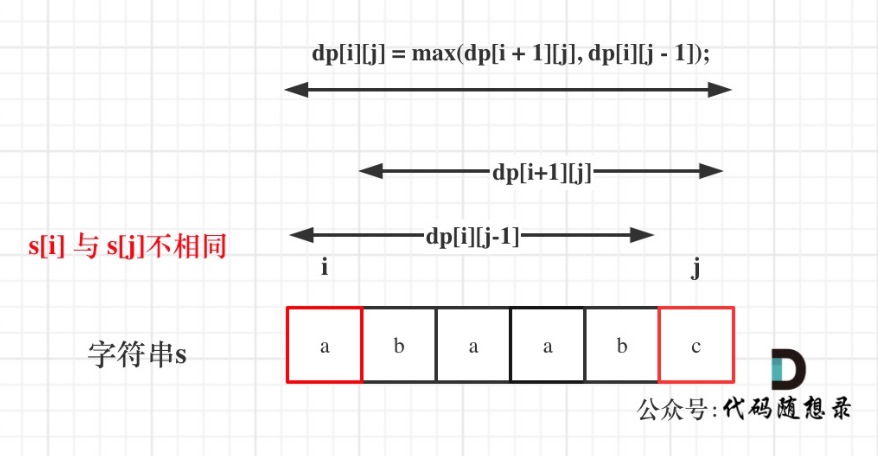
在判断回文子串的题目中,关键逻辑就是看s[i]与s[j]是否相同。
如果s[i]与s[j]相同,那么dp[i][j] = dp[i + 1][j - 1] + 2;
如果s[i]与s[j]不相同,说明s[i]和s[j]的同时加入 并不能增加[i,j]区间回文子序列的长度,那么分别加入s[i]、s[j]看看哪一个可以组成最长的回文子序列。那么dp[i][j]一定是取最大的,即:dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);
- dp数组如何初始化
当i与j相同,那么dp[i][j]一定是等于1的,即:一个字符的回文子序列长度就是1。其他情况dp[i][j]初始为0就行
- 确定遍历顺序
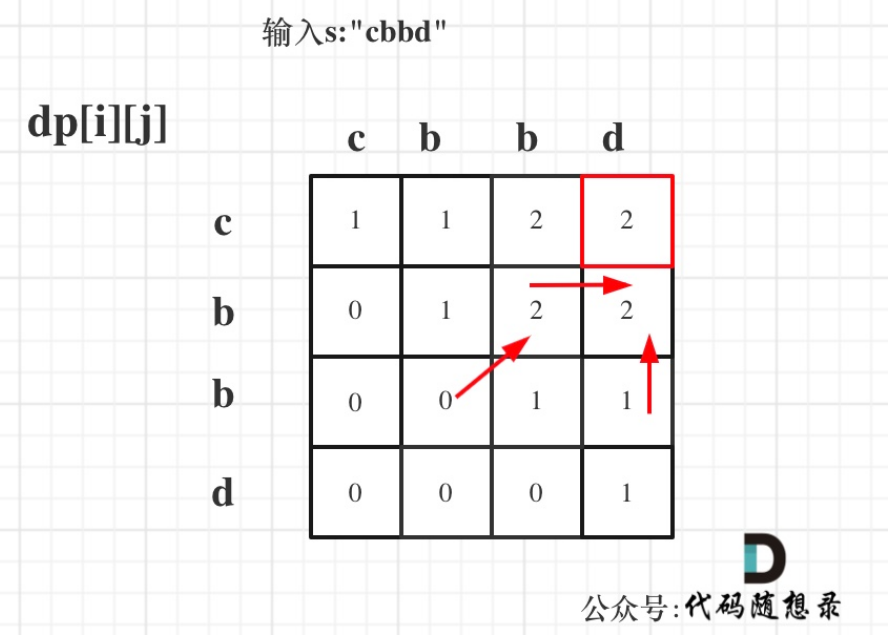
从递归公式中,可以看出,dp[i][j] 依赖于 dp[i + 1][j - 1] ,dp[i + 1][j] 和 dp[i][j - 1],所以遍历i的时候一定要从下到上遍历,这样才能保证下一行的数据是经过计算的。
- 遍历模拟
python
class Solution:
def longestPalindromeSubseq(self, s: str) -> int:
dp = [[0] * len(s) for _ in range(len(s))]
for i in range(len(s)):
dp[i][i] = 1
for i in range(len(s)-1, -1, -1):
for j in range(i+1, len(s)):
if s[i] == s[j]:
dp[i][j] = dp[i+1][j-1] + 2
else:
dp[i][j] = max(dp[i+1][j], dp[i][j-1])
return dp[0][-1]动态规划总结篇
-
动态规划基础(初步感受递推的关系)
-
背包问题系列(递推二维到一维的理解)
-
打家劫舍系列(线性递推顺序的延伸)
-
股票系列(dp数组和数据输出的巧妙设置)*
-
子序列系列(理解模拟遍历的重要性)