数据结构-栈、队列和数组

栈

栈的定义

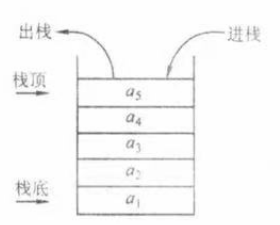
栈是只允许在一端进行插入或删除操作的线性表。首先栈式一种线性表，但限定这种线性表只能在某一端进行插入和删除操作，如图所示。

栈包括：

栈顶（Top）。允许进入插入删除的那一端。

栈底（Buttom）。不许与进行插入和删除的一端。

空栈。不含任何元素的空表。

从图中可以很明显的看到栈的操作特性为后进先出（Last In First Out， LIFO）。当我们运行高级语言程序时编译器执行语句采用的就是栈的形式。

栈的数学性质

n个不同元素进栈，出栈元素不同排列的个数为：

\\frac{1}{n+1}C\^{n}_{2n}

这公式称为卡特兰（Catalan）数。

栈的顺序存储结构

采用顺序存储的栈称为顺序栈，它利用一组地址连续的存储单元存放自栈底到栈顶的数据元素，同时附设一个指针（top）指示当前栈顶元素的位置。

栈的顺序存储类型：

复制代码

#define MaxSize 10 //定义栈中元素的最大个数

typedef struct SqStack
{
  Elemtype data[MaxSize]; //存放栈中元素
  int top;  //栈顶指针
}SqStack;

顺序栈的实现

在此代码中，以top == -1来当作栈空条件。

顺序栈的初始化

复制代码

//初始化一个空栈
void InitStack(SqStack * S){
  S->top = -1;
}

顺序栈的判空

复制代码

// 判断栈是否为空
bool StackEmpty(const SqStack *S)
{
  return S->top == -1 ? true : false; //若 top == -1 则判断为空
}

顺序栈的进栈

复制代码

//进栈操作
bool Push(SqStack *S, Elemtype x){
  //栈满结束操作
  if(S->top + 1 == MaxSize) return false;
  S->top ++; //栈顶指针指向进栈的元素位置
  S->data[S->top] = x;
  return true;
}

顺序栈的出栈

复制代码

//出栈操作                x用于接受出栈的元素
bool Pop(SqStack *S,Elemtype *x){
  //栈为空结束操作
  if(StackEmpty(S)) return false;
  *x = S->data[S->top--];
  return true;
}

获取顺序栈的栈顶元素

复制代码

// 获取栈顶元素
bool GetTop(SqStack *S, Elemtype *x)
{
  // 栈为空结束操作
  if (StackEmpty(S))
    return false;
  *x = S->data[S->top];
  return true;
}

销毁顺序栈

复制代码

//销毁栈
bool DestroyStack(SqStack *S){
  //只需将top = -1即可，因为是静态存储剩余空间会自动释放
  S->top = -1;
}

共享栈

为了更有效的利用存储空间，可以使用共享栈的形式，通过栈底位置相对不变的特性，可让两个顺序栈共享一个一位数组空间，将栈底分别设置在共享空间的两端，即0与MaxSize -1处，而当两个栈顶指针相邻时，则判断栈满。

栈的链式存储结构

采用链式存储的栈称为链栈，链栈的优点是便于多个栈共享存储空间和提高其效率。

链栈的定义

复制代码

//定义链栈类型
typedef struct StackLinkNode{
  ElemType data; //数据域 
  struct StackLinkNode *next; //指针域
};

栈的链式存储结构实现

栈的初始化

复制代码

//不带头节点初始化   用二级指针是因为传入的是以StackLinkNode*形式，原先结构体就是以指针的形式，所以要用二级指针并通过解引用的方式来进行值的修改，单传StackLinkNode形式以及用一级指针无法通过传值来对结构体类型进行修改。
void InitStackLink(StackLink ** S){
  *S = NULL;
}

入栈

复制代码

// 入栈操作 均插入到头节点后面的位置
int StackLinkPush(StackLink **S, Elemtype x)
{
  StackLink *newNode = (StackLink *)malloc(sizeof(StackLink));
  // 系统没有足够空间，插入失败
  if (newNode == NULL)
    return false;
  newNode->data = x;
  newNode->next = (*S);
  *S = newNode;

  return true;
}

出栈

复制代码

// 出栈操作 删除头节点后一个的节点  x为出栈的元素
int StackLinkPop(StackLink **S, Elemtype *x)
{
  // 判断栈是否为空
  if (StackLinkEmpty(S))
    return false;

  *x = (*S)->data;
  StackLink *p = (*S);
  (*S) = p->next;
  // 释放删除节点的空间
  free(p);
  p = NULL;
}

队列

队列的基本概念

队列的定义

队列（Queue）也是一种操作受限的线性表，只允许在表的一端进行插入，而在表的另一端进行删除。向队列中插入元素称为入队或进队。删除元素称为出队或离队。其操作的特性是先进先出(First In First Out, FIFO)

队列常见的基本操作

InitQueue(&Q)：初始化队列，构造一个空队列。
QueueEmpty(&Q)：判队列空，若队列Q为空返回true，否则返回false。
EnQueue(&Q,x)：入队，若队列Q未满，将x加入，使之成为新的队尾。
DeQueue(&Q,&x)：出队，若队列Q非空，删除队头元素，并用x返回。
GetHead(Q,&x)：读队头元素，若队列Q非空，则将队头元素赋值给x。

队列的顺序存储结构

队列的顺序存储

队列的顺序实现是指分配一块连续的存储单元存放队列中的元素（相当于操作受限的顺序表），并附设两个指针：队头指针front指向队头元素，队尾指针rear指向队尾元素的下一个位置（也可以指向最后一个元素，根据实际情况而定）。

存储类型可描述为：

复制代码

typedef struct SqQueue
{
  ElemType data[MaxSize]; // 存放队列元素
  int front, rear;        // 队头指针和队尾指针
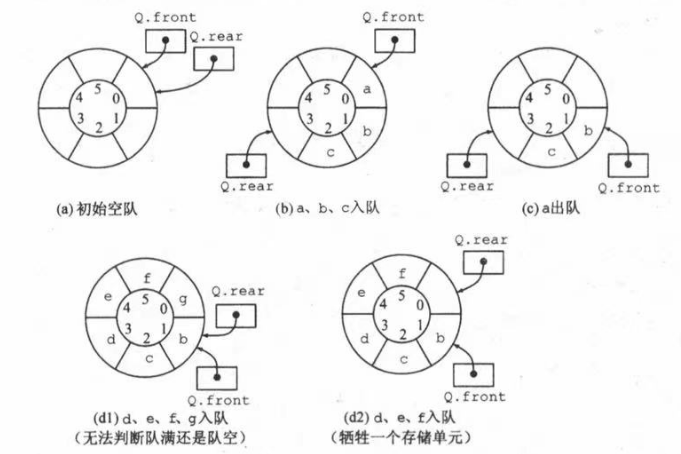
} SqQueue;

循环队列

为了解决顺序队列一些缺点，引出了循环队列的概念。将顺序队列臆造称一个环状的空间，将队列的表在逻辑上视为一个环，即称循环队列。所以当首指针Q.front = MaxSize - 1后，再前进一个位置就重新回到0，可以通过**模运算(%)**实现。

初始时：Q.front = Q.rear = 0，代表队列为空。

队首指针进1：Q.front = (Q.front + 1) % MaxSize，每当队头指针到最后一个存储空间位置就重新指回0处。

队尾指针进1：Q.rear = (Q.rear + 1) % MaxSize，逻辑与队首指针相同。

队列长度：(Q.rear + MaxSize - Q.front) % MaxSize。因为循环队列有可能会出现Q.rear > Q.front的情况，所以需要通过模运算控制最大值并保证在Q.front > Q.rear情况也可以使用。

判空条件：Q.front == Q.rear。

判断队满的三种处理方式：

牺牲一个单元来区分对空还是队满，入队时少用一个单元，即可通过(Q.front + 1) % MaxSize == Q.rear来判断是否为队满，如下图所示。

类型中增设表示元素个数的数据成员，如size。这样，队空的条件为Q.size == 0，队满的条件为Q.size == MaxSize。
类型中增加tag数据成员，以区分队满还是队空。tag = 0来代表上一个操作为删除元素，若此时Q.front == Q.rear，因为上次为删除操作，所以只有队空的情况。反之tag = 1代表插入操作，只有队满才会导致Q.front == Q.rear。

顺序存储结构队列的具体实现

初始化

复制代码

// 初始化
SqQueue *InitSqQueue()
{
  SqQueue *Q = (SqQueue *)malloc(sizeof(SqQueue));
  Q->front = Q->rear = 0;
  // 初始化队头队尾指针与存放个数
}

判空

复制代码

//判空
bool SqQueueEmpty(const SqQueue *Q){
  return Q->front == Q->rear; 
}

入队

复制代码

// 入队操作
bool EnSqQueue(SqQueue *Q, ElemType x)
{
  // 判断是否元素已满  相当于浪费了最后一个存储空间，等于只能存储MaxSize -1 个值
  if ((Q->rear + 1) % MaxSize == Q->front)
    return false;
  Q->data[Q->rear] = x;
  Q->rear = (Q->rear + 1) % MaxSize;
  return true;
}

出队

复制代码

// 出队
bool PopSqQueue(SqQueue *Q, ElemType *x)
{
  // 判断队列是否为空
  if (SqQueueEmpty(Q))
    return false;
  *x = Q->data[Q->front];

  Q->front = (Q->front + 1) % MaxSize;

  return true;
}

队列的链式存储结构

队列的链式存储

通过链表的形式来表示队列就称为队列的链式存储，它实际就是一个同时带有队头指针和队尾指针的单链表。头指针指向队头节点，尾指针指向队尾节点，即单链表的最后一个节点。

队列的链式存储类型描述为：

复制代码

//链式队列节点
typedef struct LinkNode{
  ElemType data;
  struct LinkNode *next;
}LinkNode;

//链式队列
typedef struct LinkQueue{
  LinkNode *front,*rear; //队头和队尾指针
}*LinkQueue;

队列的链式存储结构基本操作

初始化

复制代码

// 初始化
LinkQueue InitLinkQueue()
{
  LinkQueue Q = (LinkQueue)malloc(sizeof(LinkQueue));
  // 建立头节点和尾节点并指向同一块空间
  Q->front = Q->rear = (LinkNode *)malloc(sizeof(LinkNode));
  //设头节点的下一个节点为空即此时尾节点的下一个节点也为空
  Q->front->next = NULL;
  return Q;
}

判断空

复制代码

bool LinkQueueEmpty(const LinkQueue Q)
{
  return Q->front == Q->rear;
}

入队

复制代码

// 入队
bool EnLinkQueue(LinkQueue Q, ElemType x)
{
  LinkNode *s = (LinkNode *)malloc(sizeof(LinkNode));
  if (s == NULL)
    return false;
  s->data = x;
  s->next = NULL;
  Q->rear->next = s;
  //移动尾节点
  Q->rear = s;
}

出队

复制代码

//出队
bool PopLinkQueue(LinkQueue Q, ElemType *x){
  if(LinkQueueEmpty(Q))return false;

  LinkNode *p = Q->front->next;
  *x = p->data;
  Q->front->next = p->next;
  //若只有一个节点则变为空
  if(Q->rear == p){
    Q->rear == Q->front;
  }
  free(p);
  return true;
}

双端队列

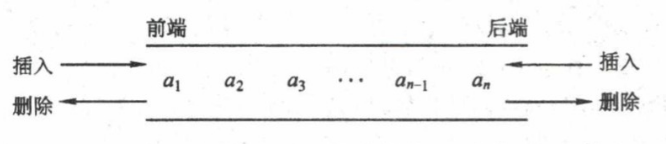
双端队列是指允许两端都可以进行入队和出队操作的队列，如图所示。其元素的逻辑结构仍是线性结构。

栈和队列的应用

栈在括号匹配中的应用

假设表达式中包含()[]这三种括号，其嵌套的顺序任意即([]())或[([][])]等均为正确格式，即左括号和右括号必定可以成一对且匹配到时为同种类型，[(])或([())或(()]均为不正确的格式。

算法分析：

当输入括号序列：[([][])] 。

计算机入栈第1个括号[后，仅当第8个括号]出现后才会出栈。
获得第2个括号(，由于)在第7个位置)才会出栈，所以也将(入栈。
第3个[由于第4个]即为相应匹配，根据就近原则，第3个和第4个有限匹配出栈，而非第1个括号。所以第3个和第4个括号匹配后就会进行出栈。
第5个和第6个和第3个第4个括号同理，也根据就近原则直接匹配成功。
此时扫描到第7个位置的)，由于前面没有其他的(，只会和第2个入栈的(进行匹配，最后匹配成功出栈。
第8个也同理，与第1个[匹配成功后出栈。
当扫描完成后判断栈是否为空，为空则匹配成功，不为空则代表匹配失败。

括号匹配代码实现

复制代码

// 括号匹配 传入括号字符串以及对应的长度
bool bracketCheck(char str[], int length)
{
  SqStack S;
  
  // 初始化栈
  InitStack(&S);
  for (size_t i = 0; i < length; i++)
  {
    // 为左括号就入栈
    if (str[i] == '(' || str[i] == '[')
    {
      Push(&S, str[i]);
    }
    else
    {
      //扫描到右括号但栈已为空
      if(StackEmpty(&S)) return false;
      Elemtype popEl;
      Pop(&S, &popEl);
      //仅当弹出的括号为一对时算匹配成功
      if (str[i] == ')' && popEl != '(')
      {
        return false;
      }
      if (str[i] == ']' && popEl != '[')
      {
        return false;
      }
    }
  }
  // 为空代表匹配成功，不为空代表匹配失败
  return StackEmpty(&S);
}

数组和特殊矩阵

数组的定义

数组是由n(n>=1)个相同类型的数据元素构成的有限序列，每个数据元素称为一个数组元素，每个元素在n个线性关系中的序号称为该元素的下标，下标的取值范围称为数组的维界。

数组与线性表的关系：数组是线性表的推广。一维数组可视为一个线性表；二维数组可视为其元素也是定长线性表的线性表。

数组的存储结构

以一维数组A[0...n-1]为例，其存储结构关系式为

LOC(a_{i})=LOC(a_{0})+i{\\times}L(0{\\leqslant}i\

其中，L是每个数组元素所占的存储单元，就是数据类型的大小（sizeof(ElemType)）。

多维数组

对于多维数组由两种映射方法：按行优先 及按列优先。

按行优先 存储的基本思想是：先行后列，先存储行号较小的元素，行号相等先存储列号较小的元素。设二维数组的行下标与列下标的范围分别为[0,h_1]与[0,h_2]，则存储结构关系式为

LOC(a_{i,j})=LOC(a_{0,0})+\[i{\\times}(h_{2}+1)+j\]{\\times}L

LOC(a_0,0)为数组的起始地址，i*(h_2 +1) + j就是行号乘矩阵的列数得到一行的个数后再加上要搜寻的元素的列号就可以搜索到元素。

例：对于数组A_[2][3]，

按行优先的存储形式为：

A_{\[2\]\[3\]}=\\begin{pmatrix} a_{\[0\]\[0\]} \& a_{\[0\]\[1\]} \& a_{\[0\]\[2\]} \\\\ a_{\[1\]\[0\]} \& a_{\[1\]\[1\]} \& a_{\[1\]\[2\]} \\\\ \\end{pmatrix} \\qquad \\underbrace{a_{\[0\]\[0\]} a_{\[0\]\[1\]} a_{\[0\]\[2\]}} \\quad \\underbrace{a_{\[1\]\[0\]} a_{\[1\]\[1\]} a_{\[1\]\[2\]}}

右边式子即先存储第一行后再存储第二行。

按列优先则存储结构关系式为

LOC(a_{i,j})=LOC(a_{0,0})+\[j{\\times}(h_{1}+1)+i\]{\\times}L

LOC(a_0,0)为数组的起始地址，j*(h_1 +1) + i就是列号乘矩阵的行数得到一列的个数后再加上要搜寻的元素的行号就可以搜索到元素。

例：对于数组A_[2][3]，

按行优先的存储形式为：

A_{\[2\]\[3\]}=\\begin{pmatrix} a_{\[0\]\[0\]} \& a_{\[0\]\[1\]} \& a_{\[0\]\[2\]} \\\\ a_{\[1\]\[0\]} \& a_{\[1\]\[1\]} \& a_{\[1\]\[2\]} \\\\ \\end{pmatrix} \\qquad \\underbrace{a_{\[0\]\[0\]} a_{\[1\]\[0\]}} \\quad \\underbrace{a_{\[0\]\[1\]} a_{\[1\]\[1\]}} \\quad \\underbrace{a_{\[0\]\[2\]} a_{\[1\]\[2\]}}

右边式子即先存储第一列后再存储第二列，最后存储第三列。

特殊矩阵的压缩存储

压缩存储：指为多个相同的元素分配一个空间，零元素不分配存储空间。

特殊矩阵：指具有许多相同矩阵元素或零元素，并且这些相同矩阵元素或零元素分布有一定规律。

对称矩阵

如图所示，以i=j为主对角线，对于矩阵A任意元素都满足：

a_{i,j}=a_{j,i}

则称为对称矩阵。对于n阶对称矩阵，可以将n阶对称矩阵A存放再一维数组B[n(n+1)/2]中，比如只放下三角部分（i>j）及主对角的元素。