图算法趣味学——启发式引导搜索

本章介绍启发式引导搜索 （heuristic-guided search）算法，有时也被称为最佳优先搜索 （best-first search）。

这些算法会利用节点到目标的估计距离等启发式信息，来决定探索节点的顺序。通过优先探索最有希望通向目标的路径，它们能够显著节省计算量。

在上一章中，我们看到，从指定起点节点到指定目标节点寻找最短（或最低成本）路径，就像我们日常在现实世界中导航一样。当我们规划去公司或商店的路线时，可以用花费的时间、行驶的距离，或者因路口复杂造成的烦躁程度，来衡量"成本"。

本章首先会解释什么是启发式，然后介绍两个经典的启发式搜索算法：

• 贪婪最佳优先搜索（Greedy Best-First Search）：仅根据节点到目标的估计成本来排序。
• A* 搜索（读作 "A-star"）：将"到当前中间节点的实际成本"和"该节点到目标的估计成本"相结合。这种结合让 A* 在高效找到优质路径方面更加强大。

选择合适的启发式

本章的算法依赖估计成本 来引导搜索。要在算法中加入启发式信息，我们必须基于每个节点已有信息，选择一种估算成本的方法。

虽然在不同问题中定义一个好的启发式的难度差别很大，但在很多真实场景里，找到合适的启发式是简单直观的。我们将先介绍欧几里得距离（Euclidean distance）作为路径规划中常用的启发式，然后讨论选择启发式时的限制和挑战。

欧几里得距离（Euclidean Distance）

欧几里得距离是一种常用、强大且直观的启发式，它通过直线距离 来估算到达目标的成本。

例如，我们要从 Boston 开车去 Seattle，如果起点坐标为 (x1,y1)(x_1, y_1)，终点坐标为 (x2,y2)(x_2, y_2)，那么它们之间的欧几里得距离为：
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> d i s t = ( x 1 − x 2 ) 2 + ( y 1 − y 2 ) 2 dist = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} </math>dist=(x1−x2)2+(y1−y2)2

在代码中可以这样表示：

def euclidean_dist(x1: float, y1: float, x2: float, y2: float) -> float:
    return math.sqrt((x1 - x2)*(x1 - x2) + (y1 - y2)*(y1 - y2))

除非你是一只能够直飞目的地的鸟，否则欧几里得距离最多 只能作为真实成本的下界 。

地图上并不是任意两座城市之间都有直达道路，即便有高速公路，它们也不太可能是笔直的------要绕过山脉、湖泊等地理障碍，这会延长旅程距离。

尽管欧几里得距离带有一定的乐观倾向，但它在路径规划中依然很有价值，例如帮我们选出合理的中途站。

比如，从 Boston 到 Seattle 的自驾游，休息站选 Cleveland 显然比选 Miami 更合理，因为 Miami 离 Seattle 甚至离 Cleveland 都更远。

在 图 8-1(a) 中，我们看到一个二维平面上的示例图；图 8-1(b) 展示了相应的边权重，它们大多与直线距离接近。但在某些情况下，边权重会大于欧几里得距离，例如节点 2 到节点 4 的权重为 3.5，可能意味着需要额外成本（如爬陡坡或走土路）。
边权重 （实际行走成本）必须 大于或等于 估计距离。

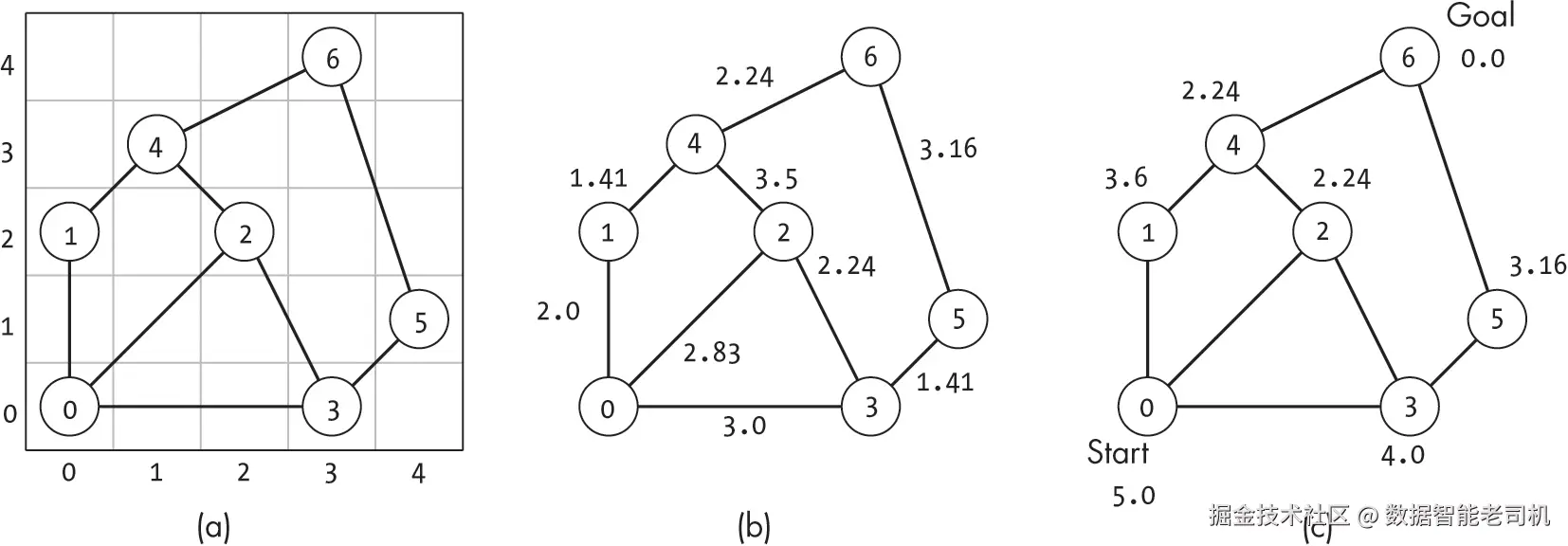
在这种布局下，我们可以通过计算每个节点到目标节点的欧几里得距离 ，来为它们提供一个潜在成本的下界估计 。

例如，在 图 8-1(c) 中，目标节点是 6 ，从节点 0 到节点 6 的估计成本为 5.0 ，对应它们的欧几里得距离。

正如之前提到的，这些估计并不总能反映真实成本。比如节点 0 到节点 6 的估计距离过于乐观，因为它们之间并没有直接的路径。

可采纳的启发式（Admissible Heuristics）

我们称一个启发式是可采纳的 ，如果从起点到目标的估计成本始终小于或等于真实成本 。

换句话说，该启发式不会高估真实成本。

例如，欧几里得距离是现实世界路径规划中一种常见、有效且可采纳的启发式，因为到目标的直线距离总是对成本的一个乐观估计。

可采纳性要求对于某些搜索（例如 A* 搜索）是必不可少的，它也是我们在为特定任务选择启发式时的主要限制条件之一。

启发式设计的挑战（Heuristic Design Challenges）

虽然为距离估算 设计启发式相对容易，但我们来考虑一个更复杂的场景：

假设你想通过职业人脉网络认识一个新联系人。每个人（节点）只能联系自己现在或过去的同事，来帮你传递请求。

为了促成引荐，你需要找到一条加权边的路径 ，间接把你和目标联系人连起来，每条边的权重表示传递请求的成本。

• 如果是每天都聊天的朋友，成本会很低。
• 如果是你永远不想再联系的讨厌前同事，成本会非常高。

在这种情况下，很难用一个可采纳的启发式准确表达所有影响因素。

你可能可以根据每个人的工作经历来做估算：

• 如果某人所在行业和目标行业差距很大，估计成本应更高（例如职业棒球选手和计算机科学家的交集很少）。
• 如果两人在同一家公司工作过，估计成本应更低。

但当你试图同时整合这些正向和负向指标时，就很难形成一个稳定的量化估计，因为这些信息太嘈杂。比如，两个人虽然曾在同一家公司工作过，但如果他们彼此不认识，甚至是死对头，这条"边"就毫无用处。

更糟的是，在这种问题中要确保启发式可采纳性更困难：

• 如果你对跨行业的联系赋予了很高的成本，有时会高估真实成本。也许你认识的一个程序员正好和一位电影明星是从小的好朋友，并且经常联系。
• 同样的，这个指标无法体现某些跨公司但关系密切的家庭成员。

一个好的启发式应当最大化信息量 、保持可采纳性 ，并且计算成本低。

• 当然，我们可以很轻松地构造一个可采纳的启发式，例如把每个节点的成本设为负无穷大，但这显然无法引导搜索。
• 我们也可以用前一章的算法（如全对最短路径）精确计算出从每个节点到目标的真实最低成本，并将其作为启发式，这样既完全可采纳又信息量最大，但这样做的计算成本极高，违背了使用启发式来减少搜索成本的初衷。

因此，在设计启发式时，必须始终权衡信息量 、计算成本 和可采纳性。

接下来，我们将介绍两种经典的启发式搜索，从最简单的方法------贪婪最佳优先搜索（Greedy Best-First Search） ------开始。

贪婪最佳优先搜索（Greedy Best-First Search）

贪婪最佳优先搜索总是选择在当前搜索点看起来最优的选项，即基于最佳启发式值估算出的最低代价，探索下一个尚未访问的节点。

该算法维护一个节点的最小优先队列（minimum priority queue）用于测试。在向目标前进的过程中，每一步都会从优先队列中选择代价最低的节点，并探索该节点。每当算法发现新的邻居节点时，就会将它们添加到队列中，并将它们的优先级设置为其启发式值。算法会一个节点接一个节点地推进，直到找到通向目标的路径。

我们可以将贪婪最佳优先搜索视为广度优先搜索的一种改进形式。广度优先搜索是按节点被发现的顺序来进行优先级排序，并使用队列来访问最早发现的节点；而最佳优先搜索则是根据启发式值来对节点进行排序。

贪婪最佳优先搜索的策略，就像一只急切而聪明的松鼠在迷宫中寻找出路（见图 8-2）。松鼠（S）能闻到目标位置（G）上那堆美味的橡子。利用它的嗅觉，松鼠能推断出一条直接通向橡子的直线路径（如果没有墙的话）（如图 8-2(a)）。

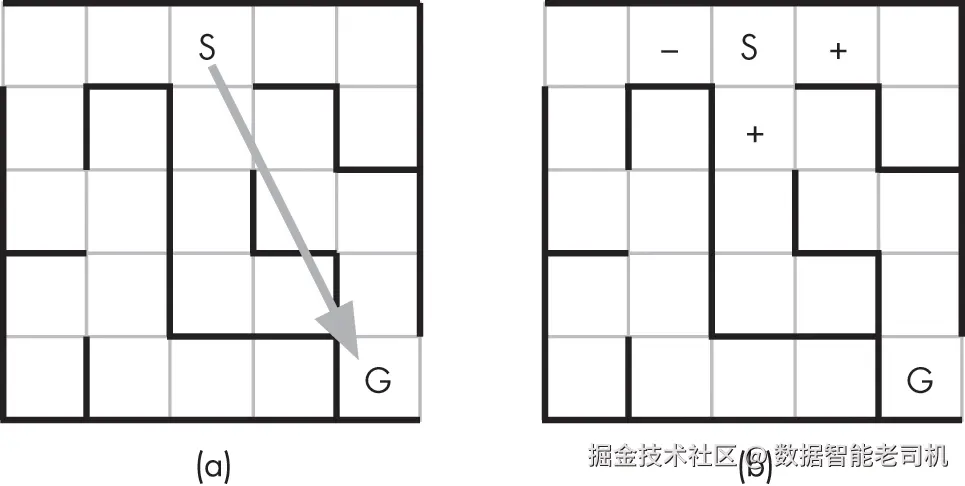
在任意一个位置（节点），松鼠也可以判断它能移动到的相邻位置，并估计哪个位置能让它更接近目标。

松鼠使用一种基于气味的启发式方法------橡子味越浓的节点离目标越近。图 8-2(b) 显示，相邻的两个方格会让松鼠更接近橡子（+），而另一个则会让它离得更远（--）。松鼠总是选择气味最浓的路径，沿着味道走向食物，有时甚至会回到气味比当前地点更浓的地方。在此过程中，它会在心里记下备用路径，并把它们加入待尝试的选项列表中。

虽然贪婪最佳优先搜索在拥有一个良好的启发式时可能很快找到一条通往目标的路径，但最终的路径并不保证是最优的。我们可能会因为在早期节点有一个过于乐观的估计而选择了一条看似不错的路径，从而错过了一条更优的路径。松鼠可能会走一条暂时远离食物的更长路线，只因为那个方向的气味当时更浓。本节后面会看到这种情况的例子。

代码实现

要实现贪婪搜索算法，我们需要在之前搜索算法的基础上增加一条额外的信息：节点的启发式值（heuristic values）。

有多种方式来提供这类信息。为了示例的清晰性，我们先使用一个预先计算好的列表 h，它将节点的索引映射到其启发式值。后面章节会介绍另一种方法。

贪婪最佳优先搜索的代码与广度优先搜索相似，只是它不使用队列按发现顺序存储节点，而是使用一个基于最小堆的自定义优先队列（见附录 B），以按启发式估计代价的升序来获取节点：

def greedy_search(g: Graph, h: list, start: int, goal: int) -> list: 
    visited: list = [False] * g.num_nodes
    last: list = [-1] * g.num_nodes
    pq: PriorityQueue = PriorityQueue(min_heap=True)

    ❶ pq.enqueue(start, h[start])
    ❷ while not pq.is_empty() and not visited[goal]:
        ind: int = pq.dequeue()
        current: Node = g.nodes[ind]
        visited[ind] = True

        for edge in current.get_edge_list():
            neighbor: int = edge.to_node
            ❸ if not visited[neighbor] and not pq.in_queue(neighbor):
                pq.enqueue(neighbor, h[neighbor])
                last[neighbor] = ind

    return last

代码首先初始化内部数据结构，包括：

• visited：标记每个节点是否被访问过；
• last：记录每个节点在搜索路径中由哪个节点到达；
• pq：最小优先队列。

然后，它将起始节点插入优先队列，其优先级为该节点的启发式代价 ❶。

在松鼠迷宫的比喻中，这一步相当于松鼠刚准备开始搜索------站在迷宫外闻到橡子的味道，并且在心里优先队列中只有一个选项：起始节点。

搜索过程在 while 循环中进行，直到优先队列为空，或目标节点已被访问 ❷。

每次循环时，代码从优先队列中取出启发式值最小的节点，并访问它------这就像松鼠跑向下一个味道最浓的地方。

接着，for 循环遍历当前节点的所有邻居。如果邻居既没有被访问，也不在优先队列中 ❸，那么就把它加入优先队列（优先级为其启发式估计值），并记录它的前驱节点。

当循环结束时，贪婪搜索要么找到了一条到目标的路径，要么确定不存在这样的路径：

• 找到路径：优先队列中可能还有未探索的节点；
• 没有路径 ：优先队列为空，last 中目标节点的值为 -1，表示无法回溯到起点。

函数最后返回 last 列表。

示例

图 8-3 展示了在图 8-1 的图结构上进行贪婪最佳优先搜索的例子。

在每个子图中：

• 当前正在探索的节点用虚线圆圈标出；
• 已访问的节点用阴影表示；
• 边上的权重标注在各条边旁。

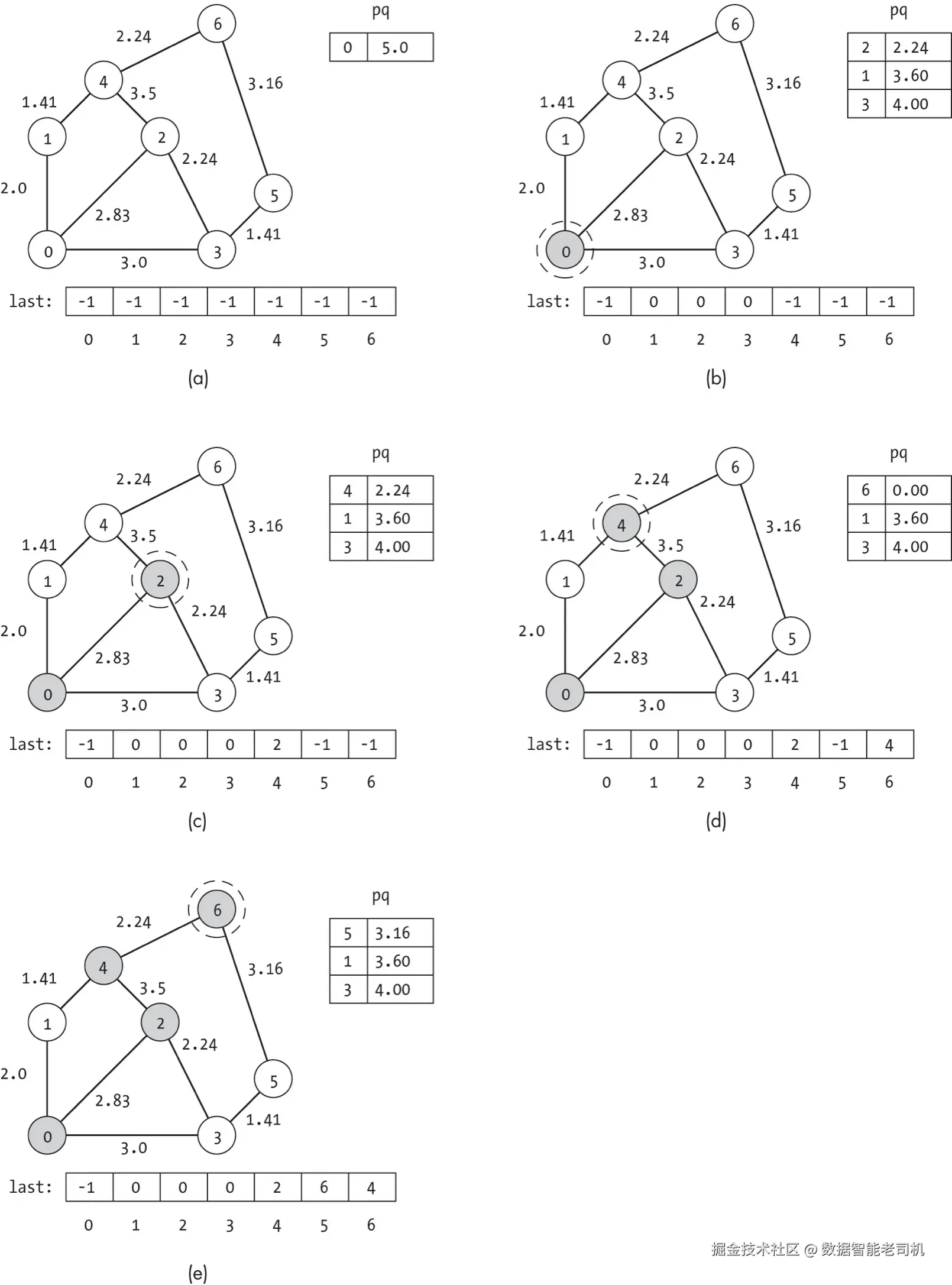
为了避免图示杂乱，图 8-3 中没有直接显示每个节点的启发式值。

不过，这些启发式值与图 8-1(c) 中所示的欧几里得距离完全相同。

我们将它们以列表 h 的形式提供给算法：

h: list = [5.0, 3.6, 2.24, 4.0, 2.24, 3.16, 0.0]

每个子图还展示了当前的优先队列（为了方便说明，按排序后的顺序显示）以及 last 列表。

虽然代码中优先队列是用堆结构维护的，但在这里我们按排序顺序展示，以更清楚地说明节点的优先次序。

搜索开始时，将起始节点以其对应的代价估计值 5.0 放入优先队列（图 8-3(a)）。

在 while 循环的第一次迭代中，从优先队列中取出节点 0，访问它，并将其所有未见过的邻居加入优先队列（图 8-3(b)）。

这些节点的优先级等于它们的启发式代价（即到目标节点的欧几里得距离，见图 8-1(c)）：

• 节点 1 = 3.6
• 节点 2 = 2.24
• 节点 3 = 4.0

同时，将这些邻居的 last 值都设为 0，表示它们是从节点 0 到达的。

搜索的每一步都会选择当前看来最有希望 的节点继续前进。

在检查优先队列后，算法选择节点 2。

如图 8-3(c) 所示，它接着将节点 2 的未访问邻居加入优先队列。

由于启发式值为 2.24，节点 4 现在位于队首。

搜索在图 8-3(d) 中访问节点 4，并最终在图 8-3(e) 到达目标节点。 从这个例子可以看出，贪婪最佳优先搜索 并不会产生到目标的最优路径。

它被节点 2 诱惑了------因为节点 2 离目标很近------但随后不得不绕行经过节点 4，并跨越一条权重为 3.5 的昂贵边。

贪婪搜索无法意识到通过节点 1 会更好，因为它不考虑到达某个节点所需路径的实际代价，而是只看 从该节点到目标的估计代价，并用它来排序。

当它访问完节点 2 时，已经发现节点 4 的启发式值优于节点 1，于是放弃了节点 1。

这种次优性可以用一次令人沮丧的骑行旅行来形象化：

假设你和朋友一早在骑行，没有目标，也没注意路线，现在又累又想回家。

你们来到一个岔路口：

• 左边的路能直接到你家旁边的路口，但中间要翻一座小山。
• 右边的路平坦，但终点离家还有几个街区。

两条路都能让你更接近家，但代价（边权）差别很大。

不幸的是，贪婪算法并不会考虑这一点。

还没等你开口，你那过于兴奋的朋友就欢呼一声，直接骑上了左边的山路。

当你试图抗议时，他只会喊："谁在乎那点小坡？这条路更近啊！"

A* 搜索

A * 搜索将贪婪最佳优先搜索的启发式估计，与对已观测路径代价 的完整考虑结合起来，从而高效地找到两个节点之间的最短路径。

贪婪搜索完全忽略 边的实际代价，而 A* 则在启发式的"美好承诺"与实际路径的"冷酷事实"之间做平衡。

这种结合使得 A* 既准确又计算高效。

A* 算法的核心直觉是：

我们要按估计的总路径代价 来给候选节点排序。

仅关注从当前节点到目标的估计代价是不够的，还必须考虑到达该节点本身的花费。

为此，A* 额外跟踪一条信息：

到目前为止，到达每个节点的最佳路径的实际代价。

如图 8-4 所示，对于未访问的节点，其优先级等于：

到该节点的最佳路径代价 + 从该节点到目标的估计代价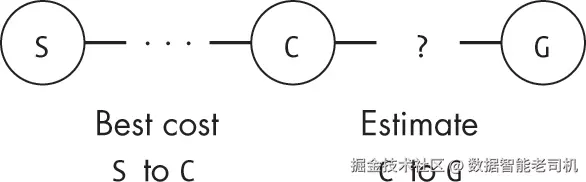

与展示贪婪最佳优先搜索的"急切松鼠"相比，我们可以把 A* 搜索想象成一个更为谨慎的探险者，他拥有高等测绘学位，正在寻找通往拟建考古挖掘点的路径。除了标准的指南针、水壶和必备的探险帽，我们的主角还携带一个笔记板，用来记录区域信息。他将每个节点表示为一行，包含三列信息：

1. Best Cost（到该节点的最佳路径代价）
2. Best Path（到该节点的最佳路径）
3. Heuristic（通过该节点到达目标的估计总代价）

在整个旅程中，探险者不断更新这三列信息。

探险者从一个村庄走到另一个村庄（节点到节点）。

• GPS 坐标提供最短可能距离的估计。
• 路标、路径标记以及实地访谈揭示实际到邻近节点的距离。

每次发现新节点时，他都会计算该节点到目标的估计代价，并写入 Heuristic 列。

在旅程中，探险者总是移动到估计总成本最低 的下一个节点。

每次考虑邻近位置（无论新节点还是已见过的节点），他都会判断是否找到了比之前更好的路径。如果是，则在 Best Cost 和 Best Path 列中记录下来。

举例：探险者早先可能发现了一条通过密集、蜘蛛出没的丛林、长度 10 英里的小径到达考古点，他在笔记中记录了这条路径及其巨大代价。后来，他发现从东侧经过一个小村庄的三英里铺装公路能到达同一地点。他立刻擦掉旧记录，并更新 Best Cost 和 Best Path 列，反映这一新发现。

代码实现

A* 搜索（Listing 8-1）按节点到目标的估计总代价 对候选节点排序。

同样使用预先计算好的启发式值列表 h。

def astar_search(g: Graph, h: list, start: int, goal: int) -> list: 
    visited: list = [False] * g.num_nodes
    last: list = [-1] * g.num_nodes
    cost: list = [math.inf] * g.num_nodes
    pq: PriorityQueue = PriorityQueue(min_heap=True)

    ❶ pq.enqueue(start, h[start])
    cost[start] = 0.0

    ❷ while not pq.is_empty() and not visited[goal]:
        ind: int = pq.dequeue()
        current: Node = g.nodes[ind]
        visited[ind] = True

        for edge in current.get_edge_list():
            neighbor: int = edge.to_node
            ❸ if cost[neighbor] > cost[ind] + edge.weight:
                cost[neighbor] = cost[ind] + edge.weight
                last[neighbor] = ind

            ❹ est_value: float = cost[neighbor] + h[neighbor]
            if pq.in_queue(neighbor):
                pq.update_priority(neighbor, est_value)
            else:
                pq.enqueue(neighbor, est_value)
    return last

代码解析

1. 初始化内部数据结构：

   • visited：记录每个节点是否已访问
   • last：记录到达每个节点的前驱节点
   • cost：记录从起始节点到每个节点的最佳路径代价
   • pq：最小优先队列

2. 将起始节点放入优先队列，并将其代价设为 0 ❶。

   在比喻中，这相当于探险者准备出发，站在起点村庄前，已知起点到自己的位置代价为 0。

3. 进入 while 循环，直到优先队列为空或到达目标节点 ❷。

   • 每次从队列中取出估计总代价最低的节点访问。

4. 对当前节点的每个邻居：

   • 检查当前路径是否提供更低代价 ❸。
   • 如果找到更好的路径，更新 cost 和 last 列表。
   • 更新邻居节点的估计总代价（cost[neighbor] + h[neighbor]）❹。
   • 若邻居已在队列中，则更新其优先级，否则加入队列。

5. 循环结束后：

   • 若找到目标节点，last 列表记录路径
   • 若无路径可达，队列空，last 对应目标节点为 -1

示例

图 8-5 展示了一个 A* 搜索例子。

• 使用的启发式与图 8-1(c) 相同：

h: list = [5.0, 3.6, 2.24, 4.0, 2.24, 3.16, 0.0]

每个子图显示了：

• 当前探索节点（虚线圈标记）
• 已访问节点（阴影）
• last 数组、cost 数组
• 优先队列（为便于说明按排序顺序展示）

图 8-5(a) 显示搜索开始前的初始状态：

• 优先队列仅包含起始节点
• 起始节点到自身代价为 0
• 估计总代价即为起始节点到目标的启发式估计
• 其他节点代价为无穷大

比喻中，这相当于探险者在出发前准备好清单，戴上头盔，说：

"我知道考古点至少离城市 5 英里，该出发了。"

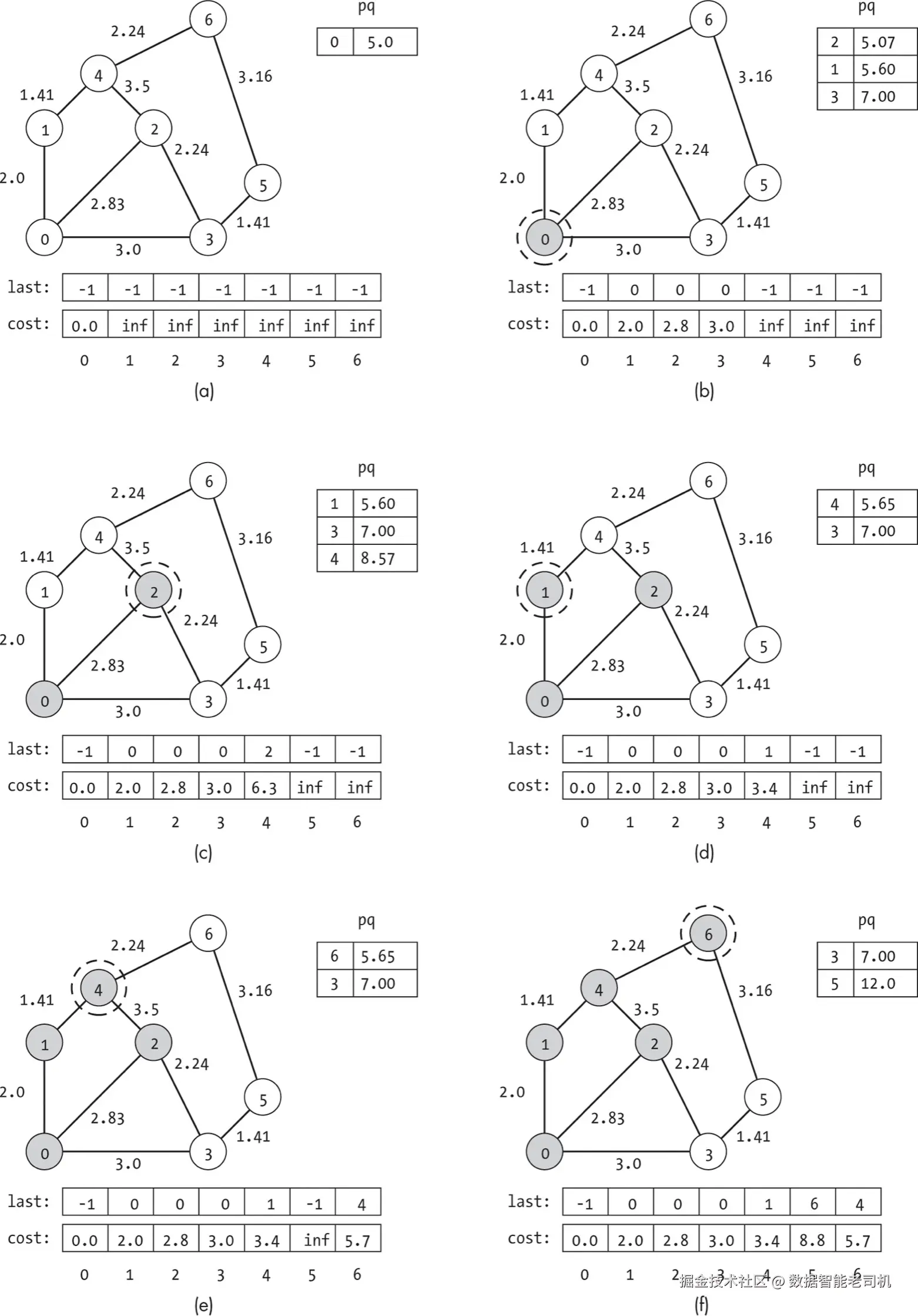
在图 8-5(b) 中，搜索从优先队列中取出顶部节点进行探索。这相当于我们勇敢的探险者到达起始城市并环顾四周。搜索发现三个邻居节点，并计算它们的预计总成本，总成本等于到当前节点的距离、到邻居的边权以及从邻居到目标的估计代价之和，结果如下：

• 节点 1：0.0 + 2.0 + 3.6 = 5.6
• 节点 2：0.0 + 2.83 + 2.24 = 5.07
• 节点 3：0.0 + 3.0 + 4.0 = 7.0

这相当于探险者在起始城市发现三条出路后更新清单。借助路标，他们知道了各村庄的距离和位置，每条道路都对应一个不同的预计总成本。

由于节点 2 的预计总成本看起来最好，搜索接下来探索它，如图 8-5(c) 所示。此时，它考虑两个邻居节点 3 和 4。节点 3 从起始节点已有更低成本（3.0 对比 2.83 + 2.24 = 5.07），因此搜索不更新其路径或优先级。节点 4 之前未被访问，因此初始成本为 2.83 + 3.5 = 6.33，总成本估计为 2.83 + 3.5 + 2.24 = 8.57。该成本反映了从节点 2 到节点 4 的路径及其高昂代价。

从探险者的视角来看，这些决策也类似。他们看到一个路标指向两个新村庄。村庄 3 还需额外 2.24 英里。相比从城市 0 直接到村庄 3，经村庄 2 再到村庄 3 的绕行路径要长得多，因此他们意识到无需添加多余的停留点，便不更新村庄 3 的记录。相反，从村庄 2 到村庄 4 的路径虽然异常困难，但有可能更接近目标，因此更新了村庄 4 的记录。

搜索继续选择预计总成本最佳的未访问节点。与贪婪搜索不同，它不会跳到预计最接近目标的节点（此例为节点 4）。虽然节点 4 的预计成本最优（2.24），但通过当前路径到达它的代价很高（经节点 2 为 6.3）。于是搜索先探索节点 1，如图 8-5(d) 所示，并找到了到节点 4 的更优路径，更新预计总成本为 2.0 + 1.41 + 2.24 = 5.65，同时更新 last 数组，表明到节点 4 的路径应经节点 1 而非节点 2。

这一步对应探险者考虑整个路线的总成本。雇佣他们的考古学家希望多次到达挖掘点的路线成本尽量低。知道这一点后，探险者选择先访问村庄 1，而不是从村庄 2 翻越山路到村庄 4。

搜索继续至节点 4（图 8-5(e)），再至节点 6（图 8-5(f)）。每到一处，它都会考虑未访问的邻居并检查是否发现更优路径。到达节点 6 后，搜索停止，因为已找到目标的最佳路径，即使节点 3 和 5 尚未访问。

为什么 A* 能找到最优路径

怀疑的读者可能会问：既然 A* 只探索图的一部分，未访问所有节点，怎么能确保找到最佳路径？实际上，只要启发式函数是可接受的（admissible），A* 总能找到最优路径。原理如下：

假设 A* 已通过某条路径到达目标节点，并考虑另一条经过未访问节点 v 的路径。由于启发式可接受且优先队列按优先级排序，任何经过节点 v 的路径成本都不会低于已找到的路径。

因为在到达目标节点前未访问节点 v，节点 v 的优先级值（估计总代价）必然大于目标节点的优先级值。到达目标节点时，其优先级值等于已找到路径的实际成本。目标节点到自身的估计成本为 0，因此其优先级值等于到前驱节点的实际成本加上相应边权，这时不再依赖启发式，而是实际路径成本。

相对地，未访问节点 v 的优先级值是实际距离的下界（由可接受启发式保证），永远不会小于真实距离。启发式是乐观估计，因此任何经过节点 v 到达目标的路径成本至少为节点 v 的优先级值，而该值大于目标节点的实际成本。因此，经过节点 v 的路径成本必然高于已找到的路径。

将 A* 应用于谜题

只要我们能生成一个有用且可接受的启发式函数，就可以将基于启发式的搜索应用于第 6 章中的谜题图，从而高效地找到解，例如囚犯与守卫的谜题。回顾一下，图 8-6 展示了该谜题的状态图（最初在图 6-8 中介绍）。

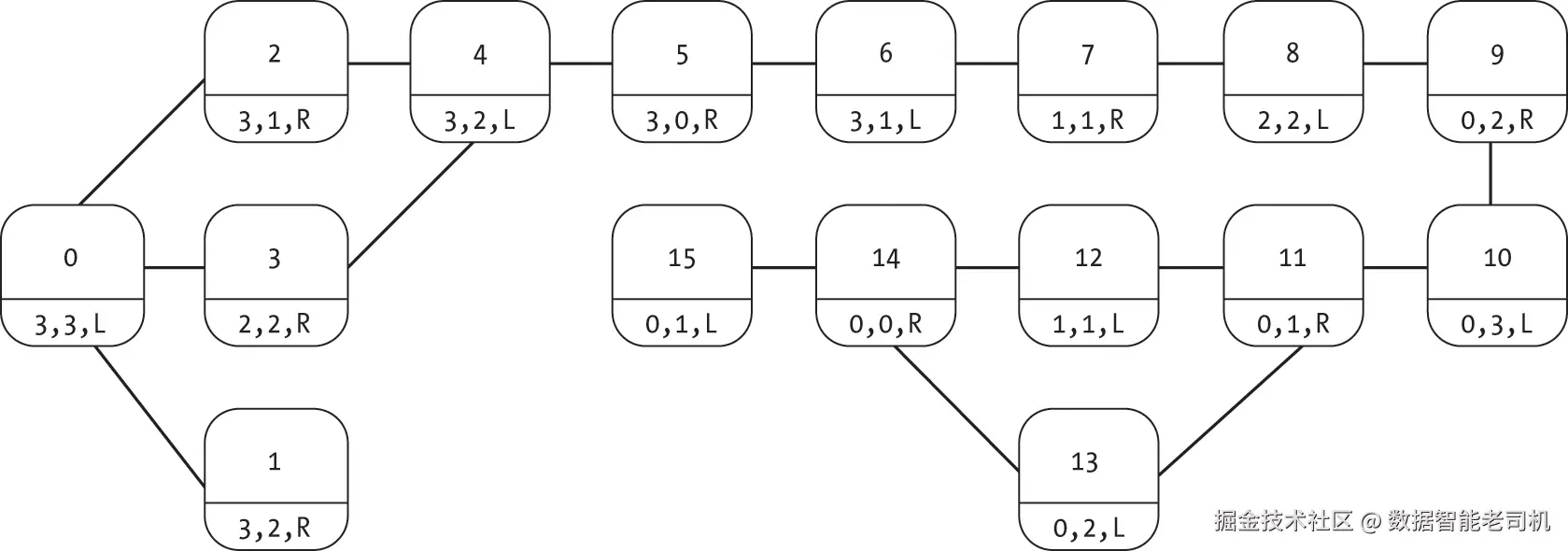
我们可以利用船的两个基本物理特性来推导出一个可接受的启发式指标，用以表示到达目标状态的距离：

1. 船最多能载两个人。如果左岸有 k 个人，那么至少需要 ceil(k / 2) 次往返才能把他们全部运到右岸。
2. 如果船在右岸，它必须先返回左岸才能接更多人。

利用这些条件，我们可以定义一个函数，从每个节点中存储的 PGState 生成启发式值：

def pg_generate_heuristic(g: Graph) -> list: 
    heuristic = [0.0] * g.num_nodes
    for node in g.nodes:
        state: PGState = node.label
      ❶ num_left: int = state.guards_left + state.prisoners_left
      ❷ min_trips_l_to_r: int = math.ceil(num_left / 2.0)
      ❸ min_trips_r_to_l: int = max(0, min_trips_l_to_r - 1)
        if not state.boat_side == "L" and min_trips_l_to_r > 0:
            min_trips_r_to_l += 1
        heuristic[node.index] = min_trips_l_to_r + min_trips_r_to_l

    return heuristic

代码通过 for 循环遍历图中的节点，检查每个节点的谜题状态以确定左岸人数 ❶。然后，它计算船从左岸到右岸所需的最少次数 ❷（考虑每次最多可运两人），并计算船从右岸返回左岸的最少次数 ❸（如果还有人待运，船必须返回左岸接人）。最终启发式值即为这两种往返次数的总和。

表 8-1 对比了此启发式函数在每个状态下的值与到达目标节点的真实距离（通过图 8-6 中从每个状态到目标的步数计算）。可以看到，该启发式函数是可接受的，从不高估真实距离。

状态	启发式距离	真实距离
3 3 L	5	11
3 2 R	6	12
3 1 R	4	10
2 2 R	4	10
3 2 L	5	9
3 0 R	4	8
3 1 L	3	7
1 1 R	2	6
2 2 L	3	5
0 2 R	2	4
0 3 L	3	3
0 1 R	2	2
1 1 L	1	1
0 2 L	1	1
0 0 R	0	0
0 1 L	1	1

有了这个启发式函数，我们就可以在渡河谜题上运行 A* 搜索：

g: Graph = create_prisoners_and_guards()
h: list = pg_generate_heuristic(g)
last: list = astar_search(g, h, 0, 14)

囚犯与守卫问题提供了一个展示 A* 搜索应用于谜题的例子，因为我们可以列出所有状态并比较启发式值与真实最优路径。然而，由于图的结构是单一的长状态序列而没有分支，A* 搜索在此谜题上并不会显著优于广度优先搜索。相比之下，在状态空间更大的谜题中，A* 搜索的优势会更明显，因为它能够专注于探索更有希望的路径。

搜索未知图

到目前为止，本章介绍的算法都是在图和启发式值已知的情况下进行搜索，但这些方法同样适用于需要动态构建未知图的问题。回想第 6 章的谜题构建例子，我们使用广度优先搜索实际探索状态空间，在遇到新节点和边时逐步构建图。我们可以用类似方式进行启发式引导的搜索。

不必为每个节点传入启发式值列表，也可以传入一个函数，根据节点中的信息动态计算启发式值。例如，如果节点包含辅助数据 x 和 y 表示其空间位置，可以定义启发式函数为该节点到已知目标位置的欧氏距离。在现实场景中，这类似于探险者用 GPS 估算他们在丛林中跋涉时到目标的距离。

我们可以用电子游戏中的"迷雾机制"来可视化这种动态构建与评估。例如，图 8-7 显示了一个 5×5 迷宫网格。已经探索的区域（如图底部的长死胡同）以方块显示，而未探索区域为灰色。灰色区域可能包含直达目标的路径、多个死胡同，甚至一只巨型怪兽，只有探索后才能知道。

本节中，我们修改了清单 8-1 的代码，通过在发现新节点时动态构建图来进行动态探索。辅助数据结构（如 last 和 distance）也必须动态扩展，以便包含新的状态。

代码说明

在示例代码中，我们通过使用一个 World 类来对算法进行泛化。这个类提供了谜题的基本信息，包括：

• 起始状态的索引
• 给定状态的邻居
• 任意两个邻居状态间的转移代价
• 状态的启发式值
• 当前状态是否为目标

有了这个接口，我们就无需事先了解状态空间。就像现实中探险者参考 GPS 和路标一样，我们在算法中使用 World 接口来检查世界的局部状态。

需要注意的是，World 类不需要列出整个状态空间，也不需要构建或存储完整的图。我们可以像第 6 章中一样，通过函数动态确定节点的邻居。动态评估允许我们在不占用大量内存的情况下探索巨大的状态空间。

本章中基于距离的示例搜索可以定义一个简单的 World 类如下：

class World:
    def __init__(self, g: Graph, start_ind: int, goal_ind: int):
        self.g = g
        self.start_ind = start_ind
        self.goal_ind = goal_ind

    def get_num_states(self) -> int:
        return self.g.num_nodes

    def is_goal(self, state: int) -> bool:
        return state == self.goal_ind

    def get_start_index(self) -> int:
        return self.start_ind

    def get_neighbors(self, state: int) -> set:
        return self.g.nodes[state].get_neighbors()

    def get_cost(self, from_state: int, to_state: int) -> float:
        if not self.g.is_edge(from_state, to_state):
            return math.inf
        return self.g.get_edge(from_state, to_state).weight

    def get_heuristic(self, state: int):
      ❶ pos1 = self.g.nodes[state].label
        pos2 = self.g.nodes[self.goal_ind].label
      ❷ return math.sqrt((pos1[0]-pos2[0])**2 + (pos1[1]-pos2[1])**2)

World 类存储底层图 (g)、起始索引 (start_ind) 和目标索引 (goal_ind)，这些信息由用户提供。类通过基本的 getter 函数提供所需信息，例如 get_start_index() 返回起始状态索引，get_neighbors() 返回邻居状态，get_cost() 返回两节点间的实际边权（若不存在边则返回无穷大）。

get_heuristic() 函数假设节点坐标存储在 label 中作为 (x, y) 元组或列表 ❶，并使用到目标的欧氏距离作为启发式值 ❷（需 import math）。构建图时，需要为节点设置包含这些坐标的 label。

动态 A* 搜索

利用 World 类，我们可以创建一个动态分配并填充数据结构的 A* 搜索版本。为简便起见，我们使用字典将每个状态的索引（或字符串）直接映射到对应信息，如清单 8-2 所示：

def astar_dynamic(w: World): 
    visited: dict = {}
    last: dict = {}
    cost: dict = {}
    pq: PriorityQueue = PriorityQueue(min_heap=True)
    visited_goal: bool = False

  ❶ start: int = w.get_start_index()
    visited[start] = False
    last[start] = -1
    pq.enqueue(start, w.get_heuristic(start))
    cost[start] = 0.0

    while not pq.is_empty() and not visited_goal:
        index: int = pq.dequeue()
        visited[index] = True
        visited_goal = w.is_goal(index)

      ❷ for other in w.get_neighbors(index):
            c: float = w.get_cost(index, other)
            h: float = w.get_heuristic(other)

          ❸ if other not in visited:
                visited[other] = False
                cost[other] = cost[index] + c
                last[other] = index
                pq.enqueue(other, cost[other] + h)
          ❹ elif cost[other] > cost[index] + c:
                cost[other] = cost[index] + c
                last[other] = index
                pq.update_priority(other, cost[other] + h)

    return last

清单 8-2 中的代码定义了 astar_search() 的修改版 astar_dynamic()。该函数创建空的辅助数据结构，并将起始状态插入每个结构中 ❶。使用字典意味着我们无需知道总状态数或其底层索引。此时，数据结构仅包含该单一状态的信息。起始状态索引通过 get_start_index() 获取，估算代价（优先级）通过 get_heuristic() 获取。

算法通过 while 循环探索优先队列中的状态，直到队列为空或找到目标。在每次迭代中，算法出队最有希望的状态（index），标记为已访问，并通过 is_goal() 检查是否为目标。在现实场景中，这类似于进入一座新城市并寻找熟悉地标。

对于每个探索状态，代码使用 get_neighbors() 返回其局部邻居 ❷，并使用 get_cost() 计算从当前节点到邻居的代价 c。同时，使用 get_heuristic() 动态计算邻居的启发式值 h。

得到邻居距离和启发式值后，代码检查该邻居是否曾被访问 ❸。如果未访问，则将其添加到每个数据结构中，邻居的代价为当前状态代价 cost[index] 加上转移代价 c，优先级为该总代价加上启发式值 h。

如果邻居已被访问 ❹，代码会比较新路径是否更优。如果找到更优路径，则更新 last、cost 和队列中的优先级。

示例

我们可以将 astar_dynamic() 应用于图 8-1 中的示例。算法并不知道图，也不知道节点数，所有信息都来自 World 类。

我们可以在贪心和 A* 示例的基础上，为节点添加空间坐标作为 label，例如：

g.nodes[1].label = [0, 2]

虽然手动设置可用于演示，但对于大量节点会非常繁琐。图数据的程序化读取方法见附录 A。

图 8-8 展示了搜索过程。图 8-8(a) 中，算法只知道起始状态索引为 0 和目标状态存在，但对图的其余部分一无所知，包括从节点 0 出发的边。目标节点甚至还没有编号，因为搜索尚未见到它。

当搜索访问节点 0 时（图 8-8(b)），它发现三条通向邻居的边。每条边的权重由 World.get_cost() 提供，启发式值由 World.get_heuristic() 提供。虽然信息不多，但足以构建起始状态周围的邻域概况。搜索通过在辅助数据结构（visited、last、cost、pq）中添加新条目来记录这些邻居，而无需显式创建图或存储边。

该搜索遵循图 8-5 中 A* 搜索示例的相同顺序。图 8-8 的主要区别在于搜索过程中对图的认知：只有当访问某节点时，才保证已看到该节点的所有边。例如，虽然算法在若干次迭代中都知道节点 1 和 4，但直到访问节点 1（图 8-8(d)）才发现它们之间的边。

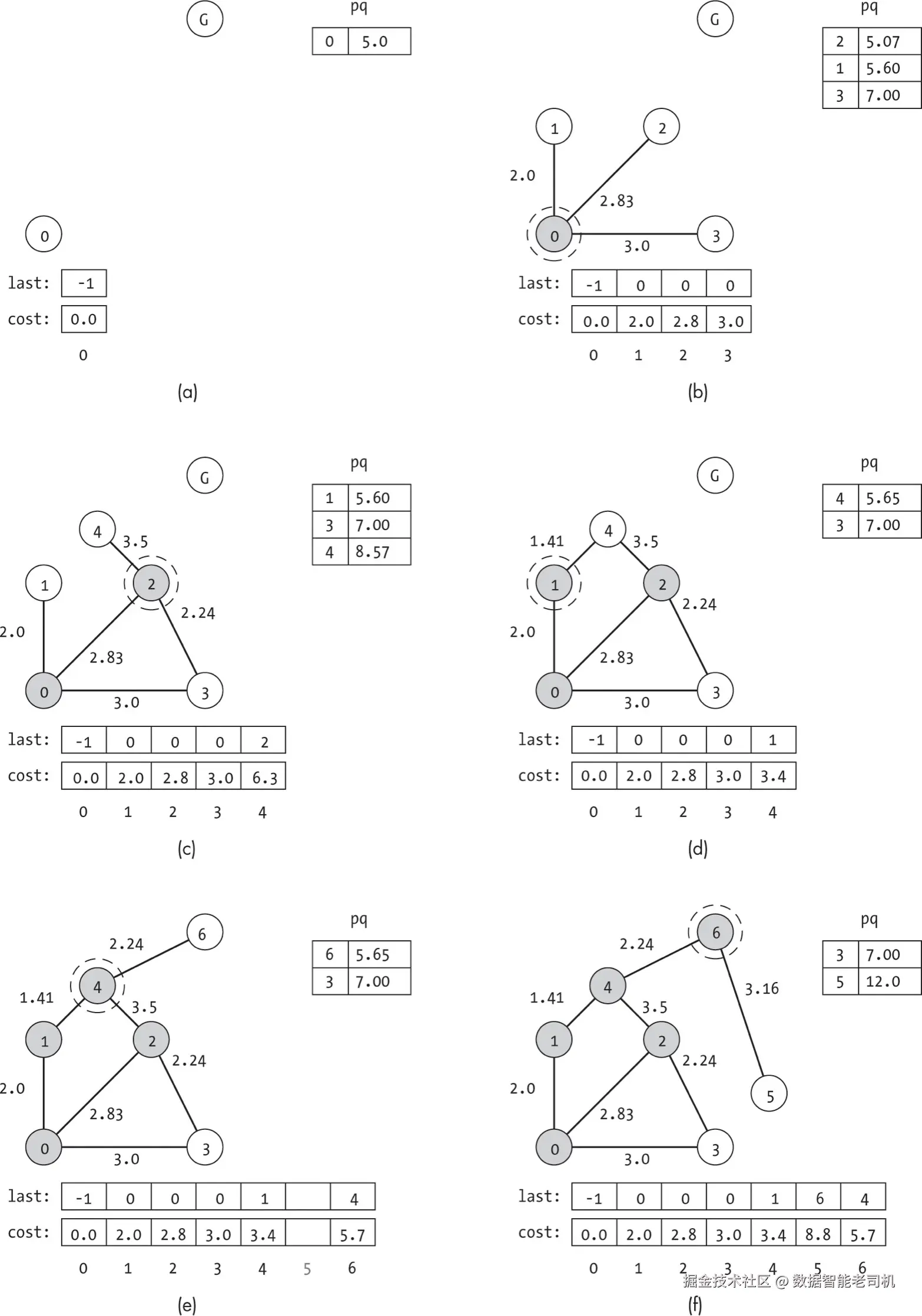
和前面的 A* 搜索示例一样，代码会持续运行，直到访问到目标节点。此时，World 类的 is_goal() 函数返回 True，我们也就知道找到了最短路径。然而，如图 8-8(f) 所示，这并不意味着搜索已经探索了整个图。它不仅跳过了节点 3 和 5，也从未了解它们之间的边。节点之外可能还有一个完整的分支世界。

这为什么重要

贪心最佳优先搜索（Greedy Best-First Search）和 A* 搜索提供了一种将启发式估计纳入搜索算法的机制，帮助我们找到两个节点之间的最优路径。贪心最佳优先搜索简单、需要追踪的信息很少，但可能产生非最优路径。而结合可接受的（乐观的）启发式估计和对当前成本的良好记录，A* 搜索能够高效地选择要探索的节点，同时保证找到最低成本路径。

这些算法，尤其是 A*，的主要优势在于启发式信息可以聚焦搜索。就像 GPS 坐标能帮助我们判断两条路哪条更快到达目的地，启发式方法让我们能够优先探索最有前景的节点。因此，A* 搜索是一种实用算法，已成为人工智能和电子游戏路径规划的核心方法。

在本书的下一部分，我们将暂时离开搜索算法，转而研究与图的连通性相关的任务。我们将回顾如何对有向图的节点进行排序，考虑如何测试图的连通性，并研究图上的随机行为。许多此类算法都将搜索作为核心组成部分。