图算法趣味学——图着色

图着色是一个概念上简单但计算上复杂的问题，在现实世界中有广泛的应用。其核心在于为无向图中的每个节点分配一种颜色，使得任意一条边连接的两个节点颜色不同。这个问题的变体包括最小化使用的颜色数量，或者在固定颜色数下寻找可行的节点着色方案。

我们可以通过欧洲地图来直观理解图着色问题的重要性。我们需要为每个国家分配一种颜色，确保相邻的两个国家颜色不同。如果法国和比利时都使用绿色，观察者可能无法辨认出两国边界。除了地图之外，图着色问题所体现的约束条件也适用于许多现实世界的优化任务。

本章首先对图着色问题进行正式定义，并更深入地讨论其现实应用场景。然后，我们将探讨几种解决方法，并说明为什么使用固定数量的颜色（或最小化使用颜色数量）的问题出乎意料地困难。

图着色问题

图着色问题是指为无向图中 <math xmlns="http://www.w3.org/1998/Math/MathML"> ∣ V ∣ |V| </math>∣V∣ 个节点分配颜色，使得任意一条边连接的两个节点颜色不同。形式化地，我们可以这样定义问题：

给定一个由节点集合 <math xmlns="http://www.w3.org/1998/Math/MathML"> V V </math>V 和边集合 <math xmlns="http://www.w3.org/1998/Math/MathML"> E E </math>E 定义的图，以及颜色集合 <math xmlns="http://www.w3.org/1998/Math/MathML"> C C </math>C，找到一个节点到颜色的分配方案，使得对于任意两个通过边 <math xmlns="http://www.w3.org/1998/Math/MathML"> ( u , v ) ∈ E (u, v) \in E </math>(u,v)∈E 连接的节点 <math xmlns="http://www.w3.org/1998/Math/MathML"> u ∈ V 和 v ∈ V u \in V 和 v \in V </math>u∈V和v∈V，满足 <math xmlns="http://www.w3.org/1998/Math/MathML"> ) c o l o r ( u ) ≠ c o l o r ( v ) )color(u) \neq color(v) </math>)color(u)=color(v)。

最小图着色问题可以定义为：找到使图具有有效着色的最少颜色数。

在本章中，我们使用图节点的 label 字段来存储该节点的颜色。颜色将用从 1 开始的整数表示，未分配的节点用 None 表示（即 node.label == None）。

Listing 16-1 定义了一个简单的 is_graph_coloring_valid() 函数，用于检查图的着色是否有效。该函数不仅可以很好地概览图着色问题的机制，同时也是测试的有用工具函数。

def is_graph_coloring_valid(g: Graph) -> bool: 
    for node in g.nodes:
      ❶ if node.label is None:
            return False
        for edge in node.get_edge_list():
            neighbor: Node = g.nodes[edge.to_node]
          ❷ if neighbor.label == node.label:
                return False
    return True

Listing 16-1：检查图着色是否有效

代码通过 for 循环遍历图中的每个节点，首先检查该节点是否被分配颜色 ❶。如果没有，则说明图的着色不完整，因此无效。如果节点已被分配颜色，代码会使用第二个 for 循环遍历该节点的每个邻居，检查两个节点是否颜色相同 ❷。如果两个邻居颜色相同，则着色无效，返回 False。如果遍历完所有节点及其邻居都未发现颜色冲突，则返回 True。

在本章的图示中，我们通过不同方向排列的哈希模式来表示不同节点的颜色，如图 16-1 所示。

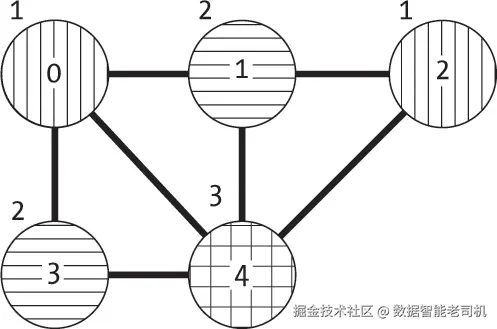
在本章的图示中，我们将在每个节点外标注颜色编号，并且颜色编号从 1 开始。

使用场景

图着色的建模方法可以应用于许多现实问题，包括地图着色、会议座位安排、停车位分配以及在迷宫中保护贵重宝物等。

地图着色

图着色的经典应用源于全球制图师和地图出版商的日常需求。为了区分地图上的不同区域，各区域必须使用不同的颜色进行标注。例如，对于如图 16-2 所示的新英格兰地图，我们可能选择将康涅狄格州涂成绿色，将罗德岛涂成橙色。

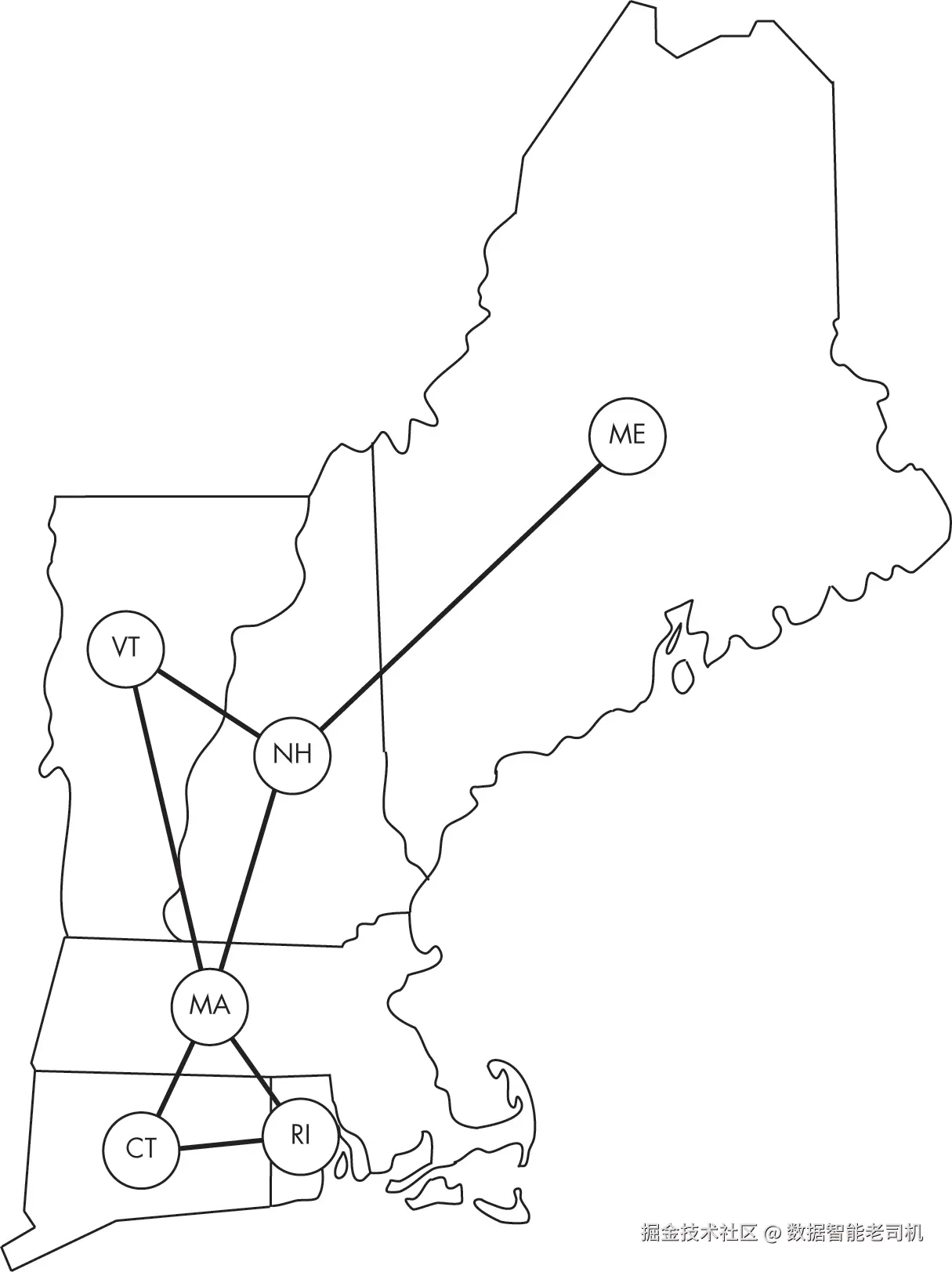
我们可以通过为每个区域创建一个节点，并在任何两个相邻区域之间添加边，将地图着色问题转换为图着色问题。在图 16-2 中，罗德岛节点与康涅狄格州和马萨诸塞州的节点都有边相连。制图师的目标就是找到一个有效的图着色方案。

安排座位

咖啡爱好者数据结构年会是一次欢乐但出人意料地政治化的聚会。社区内部在咖啡偏好和数据结构选择上存在深刻分歧，包括浅烘焙与深烘焙阵营的竞争、30 多个自豪宣称最爱数据结构的小团体，以及不可避免地在任何计算机科学讨论中引发的编程语言之争。并非所有偏好差异都会引发争论，但会引发争论的情况通常导致数小时的唇枪舌剑。每年，组织者都面临一项艰巨任务：在开幕宴会上分配桌位，确保不会发生大声争吵。

组织者长期将这次聚会作为测试新图着色算法的机会。将每位与会者建模为一个节点，将强烈的意见分歧建模为边，宴会座位的主席尝试为与会者分配桌位，使同桌的人之间没有强烈分歧。节点的颜色对应于桌位分配。

在最简单的情况下，组织者可以将桌子分配给最小的、内部一致的小派系。比如为唯一一个喝浓缩咖啡、使用 Fortran 编程的哈希表爱好者分配一张桌子，这相当于为该节点分配一个完全独特的颜色。然而，这种方法过于浪费，几乎会让每位与会者都有自己的桌子。实际上，这位哈希表爱好者可以与喜欢浓缩或深烘焙咖啡的人、Fortran 或 Cobol 用户以及大多数数据结构爱好者相处得很好。宴会主席的目标是尽量减少桌子数量（即图的颜色数量），同时确保不会引发争吵。

分配停车位

"数据结构与咖啡"书店在一天中都有源源不断的顾客。为了满足需求，店主决定增加员工。经过多轮面试，他们雇佣了六名员工，并制定了如图 16-3(a) 所示的排班表，规定新员工全天轮班。然而，还有一个问题：应为员工预留多少个停车位？

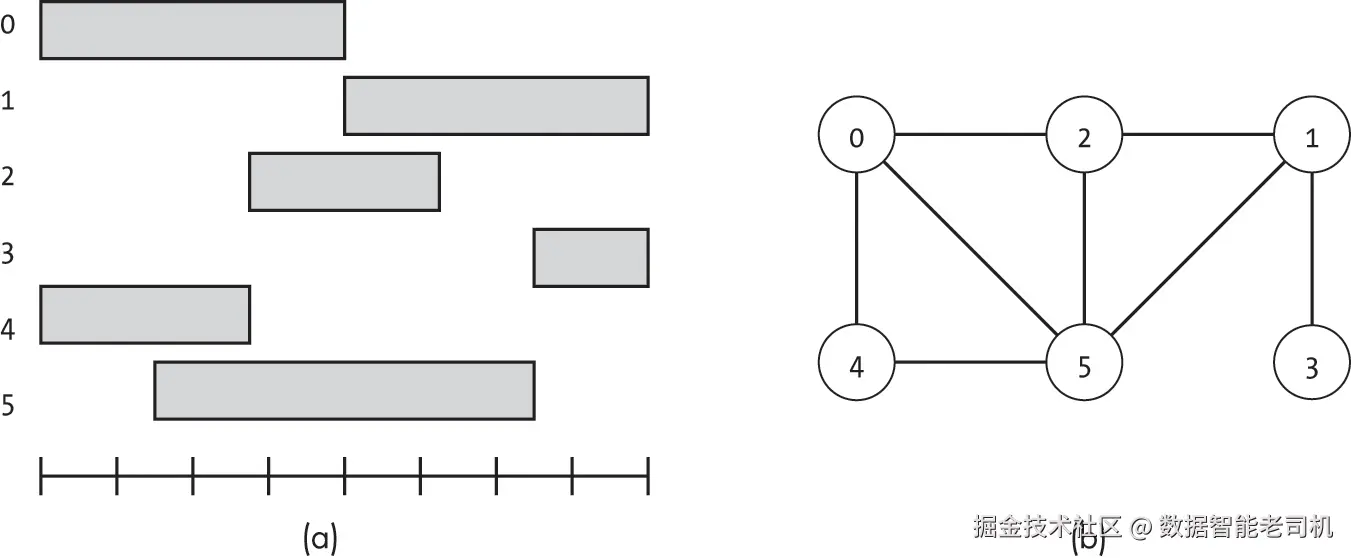
利用他们在数据结构方面的专长，店主很快把这个问题转化为图着色问题。如图 16-3(b) 所示，每位员工成为图中的一个节点，任何两个工作时间有重叠的员工之间都添加一条边，因为他们需要同时使用停车位。例如，员工 1 的排班与员工 2、3 和 5 重叠，但与员工 0 或 4 不重叠，这意味着员工 1 可以与后两位员工中的任意一人共享一个停车位。如果店主能找到一个最多使用 C 种颜色的图着色方案，那么他们最多只需预留 C 个停车位即可。

设计魔法迷宫

一个邪恶的巫师决定建造一个魔法迷宫来保护他最珍贵的宝物------能演奏他最爱歌曲的号角。为了保护"美妙音乐号角"免受冒险者的追击，巫师在迷宫中布满了各种陷阱和怪物。

然而，巫师很快遇到了问题。由于通道（边）的数量众多，很多房间（节点）都是互相连接的。他们不希望因为在相邻的两个房间放置同样的怪物而被认为懒惰。迷宫设计的技巧关系到声誉；即使是最初级的冒险者，也会对那些在房间里重复设置相同挑战的建筑师失去尊重。然而，巫师希望通过批量订购怪物来降低成本。他们需要确定使用最少数量的怪物（颜色），以确保没有相邻的房间出现相同的怪物。

图着色算法

计算机科学家和数学家开发了多种算法来解决图着色问题，但每种方法都有权衡。一些算法使用启发式方法可以找到解，但可能需要过多颜色；另一些算法在大图上计算开销很大。

图着色是一个 NP 难问题，非正式地说，这意味着目前没有已知算法能保证其最坏情况下的运行时间与数据规模呈多项式关系。需要考虑的状态数量实际上呈指数增长：对于一个有 <math xmlns="http://www.w3.org/1998/Math/MathML"> ∣ V ∣ |V| </math>∣V∣ 个节点和 <math xmlns="http://www.w3.org/1998/Math/MathML"> C C </math>C种颜色的问题，需要考虑 <math xmlns="http://www.w3.org/1998/Math/MathML"> ∣ V ∣ C |V|^C </math>∣V∣C 个状态。然而，并非全是坏消息。虽然最坏情况下问题很复杂，但许多算法在实际应用中表现良好，可以应用于许多日常问题。

本节中的算法用于搜索有效的图着色方案。如果找到，它们返回 True 表示成功，并将颜色分配设置在节点的 label 字段中，而不是返回一个单独的数据结构。如果无法找到有效的分配集合，则返回 False。

穷举搜索

穷举搜索所有可能的节点-颜色分配是一种全面的方法，如果存在有效的图着色方案，保证可以找到它：

def graph_color_brute_force(g: Graph, num_colors: int) -> bool: 
    options: list = [i for i in range(1, num_colors + 1)]

  ❶ for counter in itertools.product(options, repeat=g.num_nodes):
      ❷ for n in range(g.num_nodes):
            g.nodes[n].label = counter[n]
      ❸ if is_graph_coloring_valid(g):
            return True

  ❹ for n in range(g.num_nodes):
        g.nodes[n].label = None
    return False

代码使用 Python 的 itertools 包中的 product 函数枚举每一种可能的颜色分配组合 ❶。最初，counter 的每个值都分配为第一个颜色（1）。在每次迭代中，counter 的值会改变。

在 for 循环的每次迭代中，代码将分配值复制到节点的 label 中 ❷，并检查其是否有效 ❸。如果有效，则立即返回 True 表示已找到解，否则继续下一种组合。如果找不到有效组合，函数返回 False。在返回之前，会将所有节点的 label 重置为 None，因为没有有效的着色方案 ❹。

当然，随着图规模增大，穷举搜索的代价可能非常高。如果图有 <math xmlns="http://www.w3.org/1998/Math/MathML"> ∣ V ∣ |V| </math>∣V∣ 个节点且使用 <math xmlns="http://www.w3.org/1998/Math/MathML"> C C </math>C 种颜色，可能需要测试 <math xmlns="http://www.w3.org/1998/Math/MathML"> ∣ V ∣ C |V|^C </math>∣V∣C 种分配组合，才能找到有效方案或确认没有 <math xmlns="http://www.w3.org/1998/Math/MathML"> C C </math>C 色分配可行。图 16-4 展示了对图 16-1 中的五节点图进行三色穷举搜索的前六次迭代。搜索从所有节点使用相同颜色开始，如图 16-4(a) 所示，然后逐步遍历其他组合。

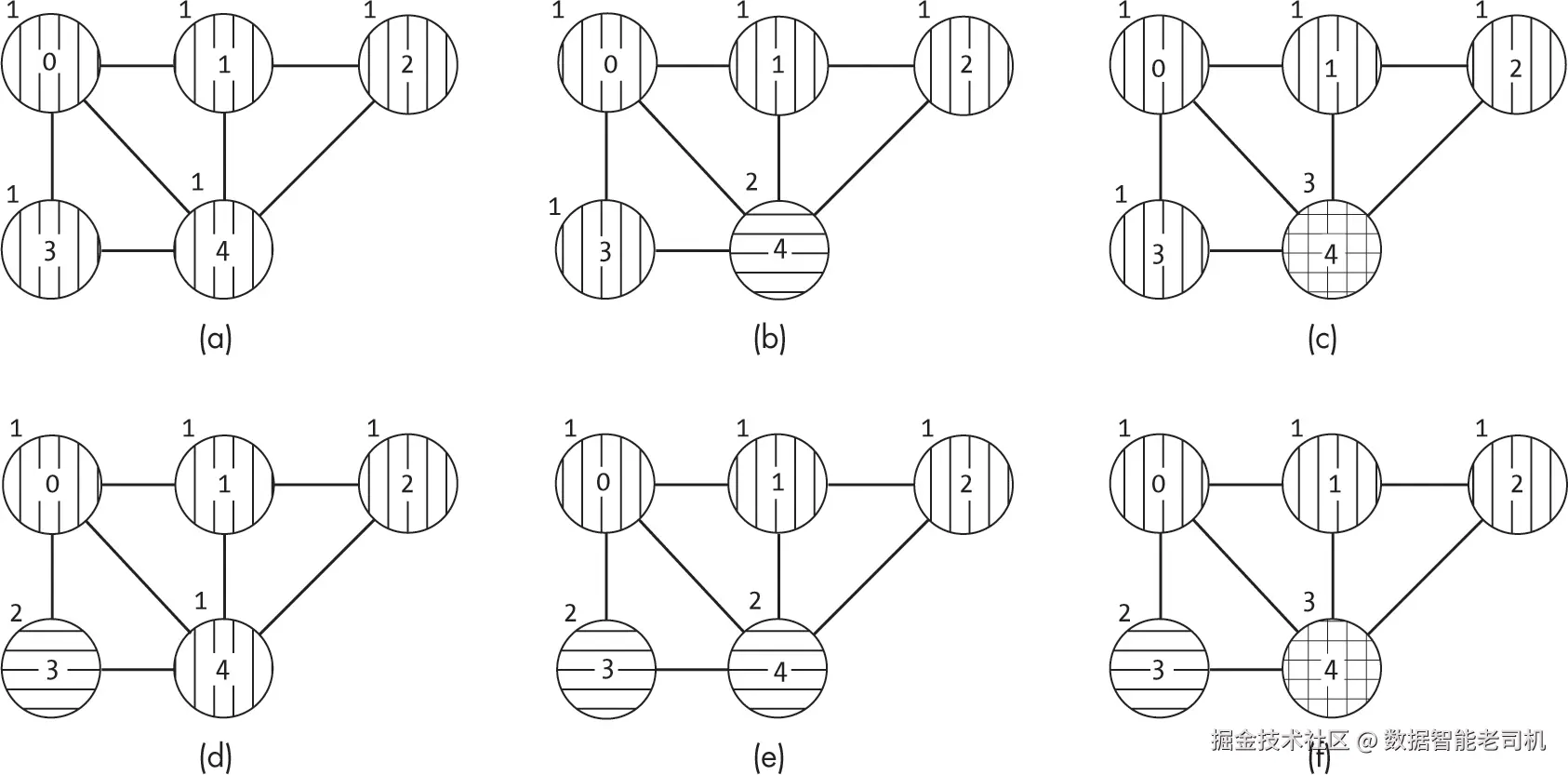
如图 16-4 所示，穷举搜索可能会浪费大量时间，一次又一次地检查那些显而易见的无效状态。它提供了简单性和完整性，但效率很低。除非图中没有边，否则所有节点都使用相同颜色显然是不可能的。想象一下，如果一个人采用这种方法，他们必须不断测试那些显然行不通的组合，因为图中某处存在明显冲突，那种挫败感会有多大。

回溯搜索

我们也可以使用递归回溯搜索来实现上一节中的迭代式穷举搜索。与前几章（尤其是第 4 章）使用的深度优先搜索不同，这种回溯搜索并不是通过邻居探索单个节点，而是将搜索状态定义为颜色分配集合本身。我们递归地探索将颜色分配给节点的所有可能方式，当发现某种分配不可行时便回溯。在我们的搜索中，每个状态对应于节点颜色的部分分配，如图 16-5 所示。

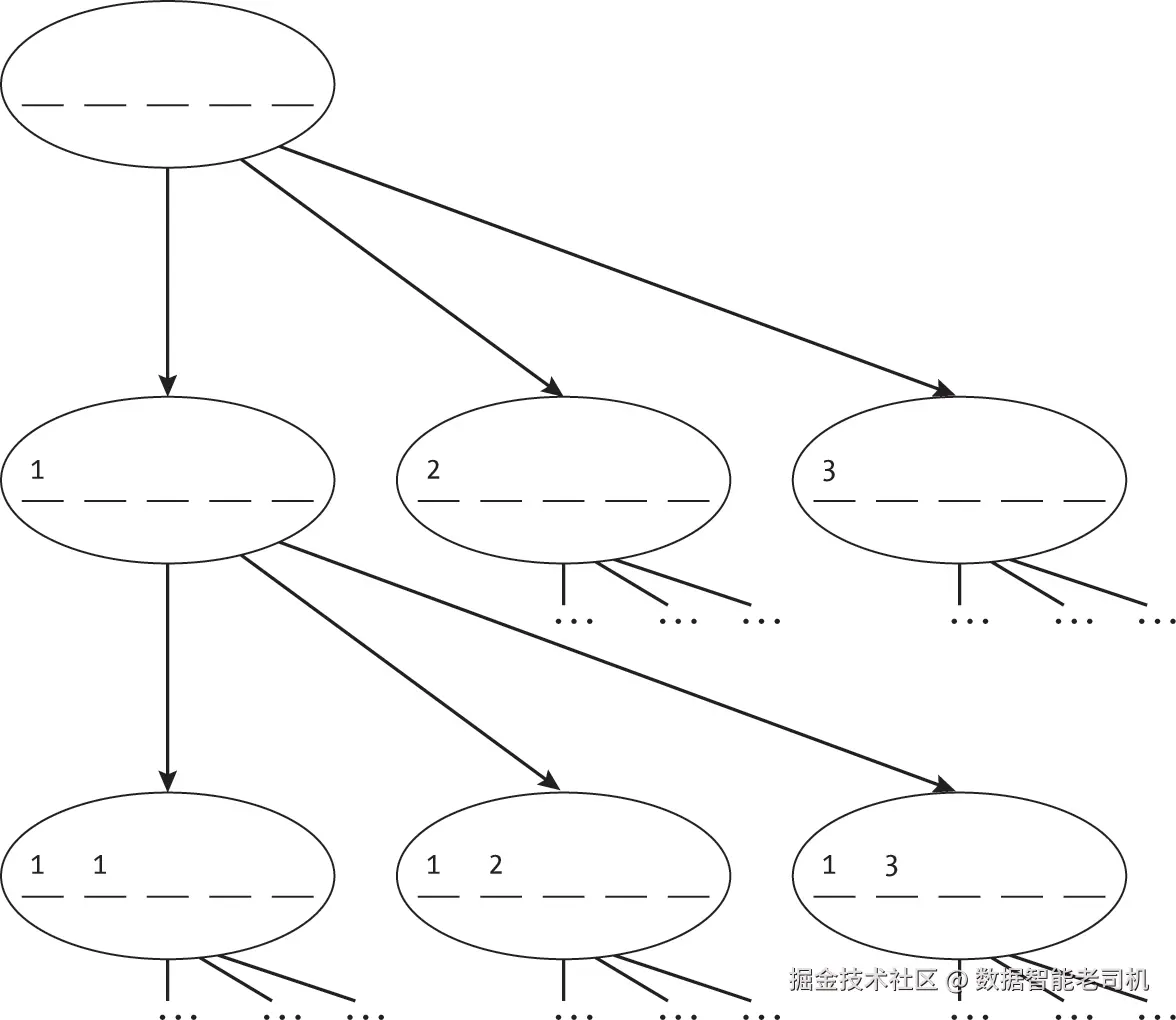
我们可以首先将搜索空间建模为与迭代式穷举搜索相同的形式，使用不带任何剪枝的深度优先搜索（我们稍后会改进这种方法）。这种搜索通过给下一个未分配的节点指定颜色来推进到相邻状态，如清单 16-2 所示。

def graph_color_dfs(g: Graph, num_colors: int, index: int=0) -> bool: 
    if index == g.num_nodes:
        return is_graph_coloring_valid(g)

    for color in range(1, num_colors + 1):
        g.nodes[index].label = color
        ❶ if graph_color_dfs(g, num_colors, index + 1):
            return True

    ❷ g.nodes[index].label = None
    return False

清单 16-2：颜色分配的递归穷举搜索

graph_color_dfs() 代码使用递归搜索，将每种颜色分配给每个节点。它从基例开始，检查是否所有节点都已分配，如果是，则检查该分配是否有效。如果还有更多节点需要分配，代码就会迭代当前节点的所有可能颜色。对于每种颜色，代码继续对下一个节点（按索引）进行递归搜索。如果分配导致有效解，则返回 True ❶。如果搜索没有找到有效分配，它会将当前节点的颜色重置为 None ❷ 并通过返回 False 回溯。

清单 16-2 中的回溯搜索实现只是迭代式穷举搜索的另一种实现方式，并未提升效率。图 16-6 展示了搜索如何像图 16-4 中的穷举搜索一样，先迭代到第一个死胡同。当搜索推进到图 16-6(e) 中的死胡同时，算法回溯并尝试为节点 4 分配新的颜色，如图 16-6(f) 所示。

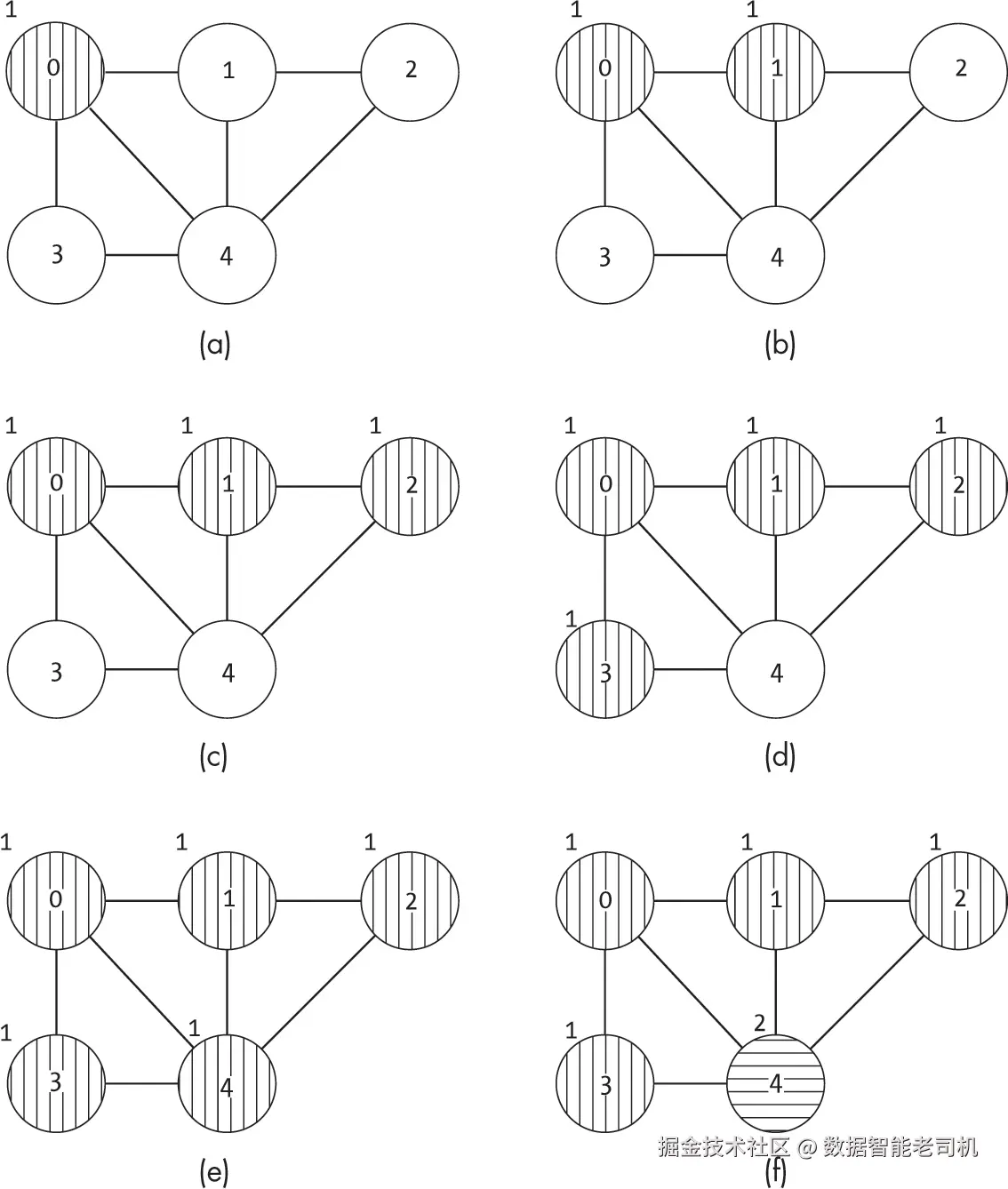
然而，我们可以通过提前剪枝并仅探索有效路径来显著提高搜索效率。在给节点分配颜色之前，我们可以先检查该分配是否会产生冲突。如果会产生冲突，不仅可以跳过该分配，还可以跳过由此分配衍生的所有后续递归。如图 16-7 所示，当给节点 0 和节点 1 都分配颜色 1 时，我们可以直接跳过整个可能性子树。相反，一旦将颜色 1 分配给节点 0，我们只考虑相邻节点 1 的颜色 2 和颜色 3。

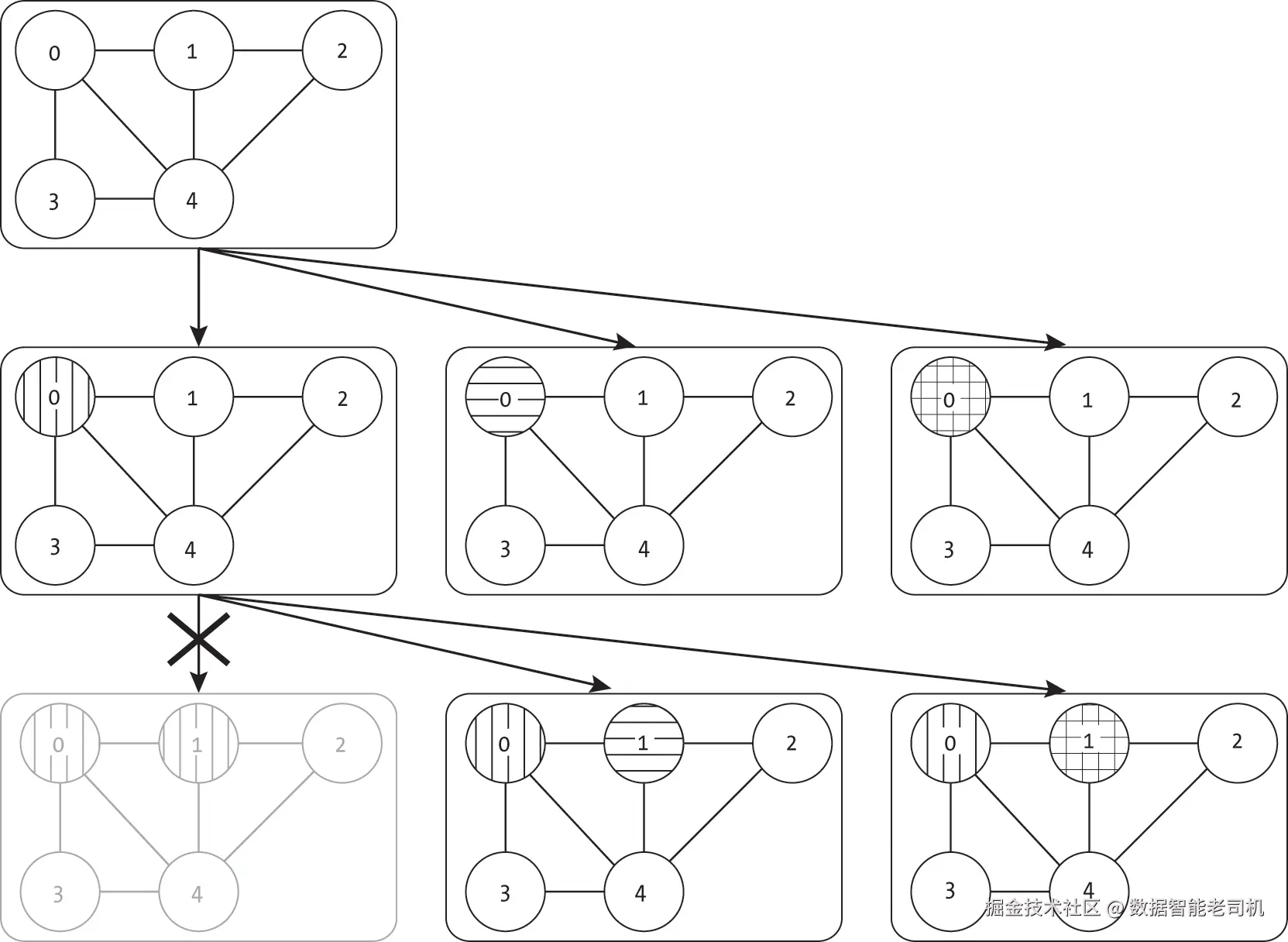
带剪枝的回溯搜索代码只需做一个小修改。在给节点分配颜色之前，我们先检查其邻居是否已有相同颜色。这个简单的检查可以防止搜索深入到无效的死胡同：

def graph_color_dfs_pruning(g: Graph, num_colors: int, index: int=0) -> bool: 
    if index == g.num_nodes:
        return True

    for color in range(1, num_colors + 1):
        ❶ is_usable: bool = True
        for edge in g.nodes[index].get_edge_list():
            if g.nodes[edge.to_node].label == color:
                is_usable = False

        if is_usable:
            ❷ g.nodes[index].label = color
            ❸ if graph_color_dfs_pruning(g, num_colors, index + 1):
                return True
            g.nodes[index].label = None

    return False

代码同样从基例开始，检查所有节点是否已分配，如果已分配则返回 True。它不需要在每次分配后检查当前分配的有效性，因为在分配颜色之前就已经做了检查。

如果还有节点需要分配，代码会遍历当前节点的所有可能颜色。首先检查邻居节点是否已经使用了该颜色，如果是，则将其标记为不可用 ❶。若颜色可用，则将其分配给当前节点 ❷，并递归探索下一个节点 ❸。如同 Listing 16-2 的方法，如果找到有效分配则返回 True，否则在不得不回溯时返回 False。

图 16-8 展示了在一个五节点示例图上、颜色数 C=3 的剪枝回溯搜索。

在搜索的最初几步中，搜索为节点 0（图 16-8(a)）、节点 1（图 16-8(b)）、节点 2（图 16-8(c)）和节点 3（图 16-8(d)）分配了有效颜色。当到达节点 4 时，搜索发现进入了死胡同：三个潜在颜色都无法分配给该节点。搜索回溯到节点 3 的分配处，但没有帮助，因为节点 3 当时只有一种可能的有效分配。搜索再次回溯，并在节点 2 尝试不同的分配（图 16-8(e)）。当搜索在图 16-8(f) 再次遇到死胡同时，它回溯到节点 1 并尝试新的颜色（图 16-8(g)）。有了节点 1 的新分配后，搜索能够顺利找到其余节点的有效分配。

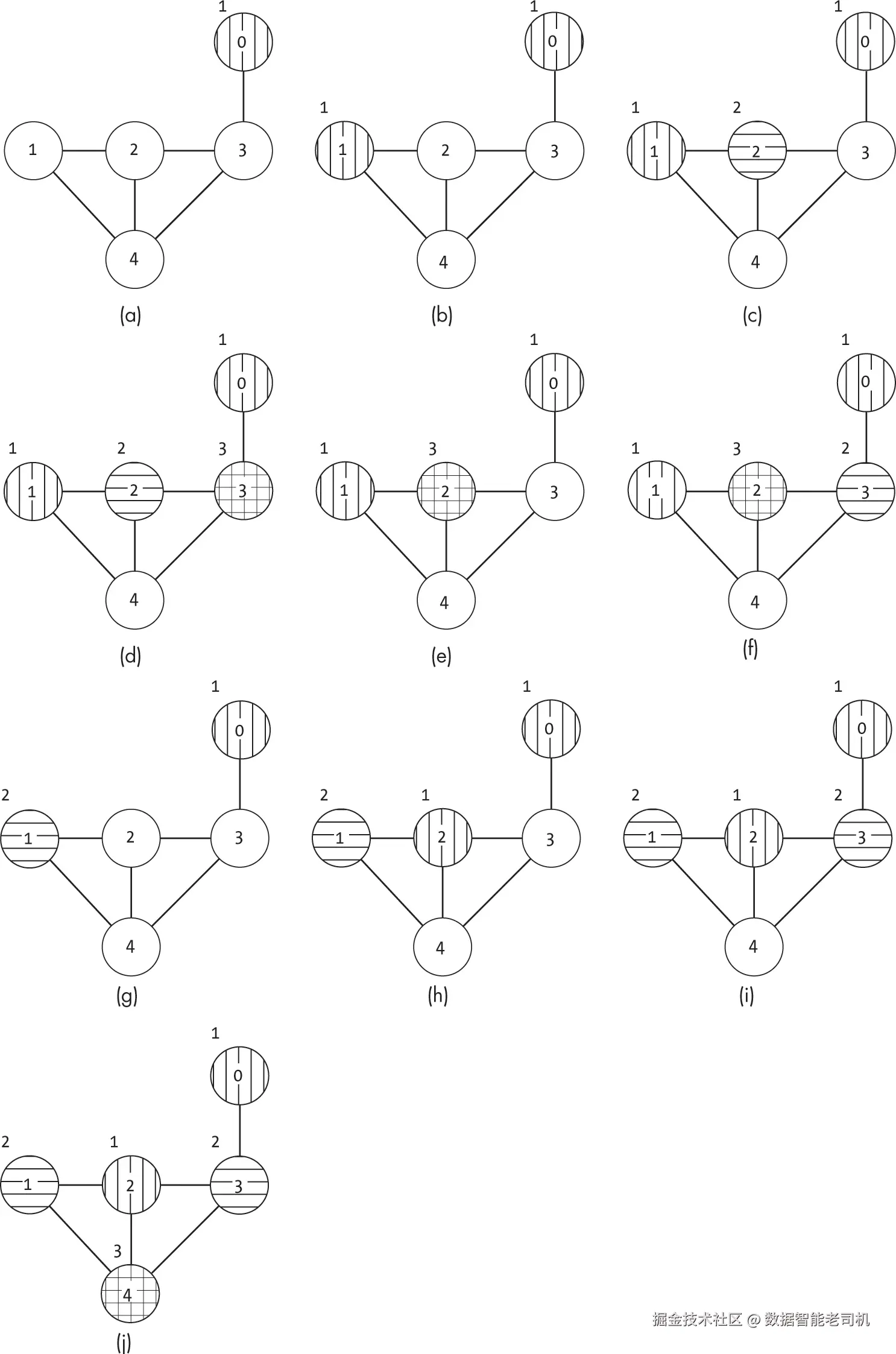
带剪枝的回溯搜索就像一位有条理的会议策划师，手里握着一块好用的橡皮。他们从逐个分配桌位开始，每次分配之前都会检查桌上是否存在已知冲突。如果有冲突，就跳过这次分配，避免浪费精力------如果已经知道分配会引发"B 树与红黑树哪个更优秀"的大吵大闹，那么继续搜索剩下的方案毫无意义。然而，这种有效性检查也只能提供有限帮助。策划师仍可能遇到死胡同，比如当前的人找不到可用桌位。如果每张桌上都至少有一位 Python 爱好者，那么热衷 LISP 的程序员就无处可坐。策划师只好叹口气，拿出橡皮，回溯到之前可以做出不同分配的节点。

贪心搜索

除了这些精确但计算开销大的方法外，我们还可以考虑启发式方法。图着色的贪心方法一次处理一个节点，为其选择第一个不会与已分配邻居冲突的颜色。与本节介绍的穷举算法不同，这里的贪心搜索并不考虑颜色的最大数量。虽然它总能找到某种解，但由于贪心特性，它未必能使用最少的颜色。

贪心搜索的代码以一个辅助函数开始，该函数通过检查邻居已使用的颜色，找到节点可用的第一个颜色，如 Listing 16-3 所示：

def first_unused_color(g: Graph, node_index: int) -> int: 
    used_colors: set = set()
    for edge in g.nodes[node_index].get_edge_list():
        neighbor: Node = g.nodes[edge.to_node]
        ❶ if neighbor.label is not None:
            used_colors.add(neighbor.label)

    ❷ color: int = 1
    while color in used_colors:
        color = color + 1
    return color

first_unused_color() 函数使用 used_colors 集合收集邻居节点的颜色，方便插入和查重。代码遍历每个邻居，将其颜色加入集合中。未分配颜色的邻居（neighbor.label == None）被跳过，因为它们不会产生冲突 ❶。最后，使用 while 循环找到第一个不在 used_colors 中的颜色 ❷。虽然效率不高，但循环总能找到一个可用颜色。

有了这个辅助函数，贪心搜索可以用一个简单循环实现：

def graph_color_greedy(g: Graph) -> bool: 
    for idx in range(g.num_nodes):
        g.nodes[idx].label = first_unused_color(g, idx)
    return True

graph_color_greedy() 函数通过索引 idx 遍历所有节点，每个节点调用 Listing 16-3 的辅助函数，找到第一个不会与邻居冲突的颜色。为了与本章其他算法一致，函数返回 True 表示找到有效着色。

我们可以用数据结构大会宴会桌安排的会议主席视角来理解贪心算法。组织者依次遍历与会者列表，为每个人分配桌位。每分配一个人，就检查已有桌上是否会产生冲突，这相当于检查当前节点是否与桌上已分配节点共享边。如果冲突，就跳到下一个桌位。如果桌位不够，则叹气，抱怨编程语言争论的荒谬，并在会场加一张桌子。

图 16-9 展示了这种贪心搜索。在图 16-9(a) 的第一次迭代中，代码为节点 0 分配颜色。在图 16-9(b) 中，考虑节点 1，由于它与节点 0 相邻，不能重复颜色 1，因此分配颜色 2。图 16-9(c) 中，节点 2 的唯一已分配邻居是颜色 2，因此分配颜色 1。搜索如此继续，直到为所有节点分配颜色，如图 16-9(e) 所示。

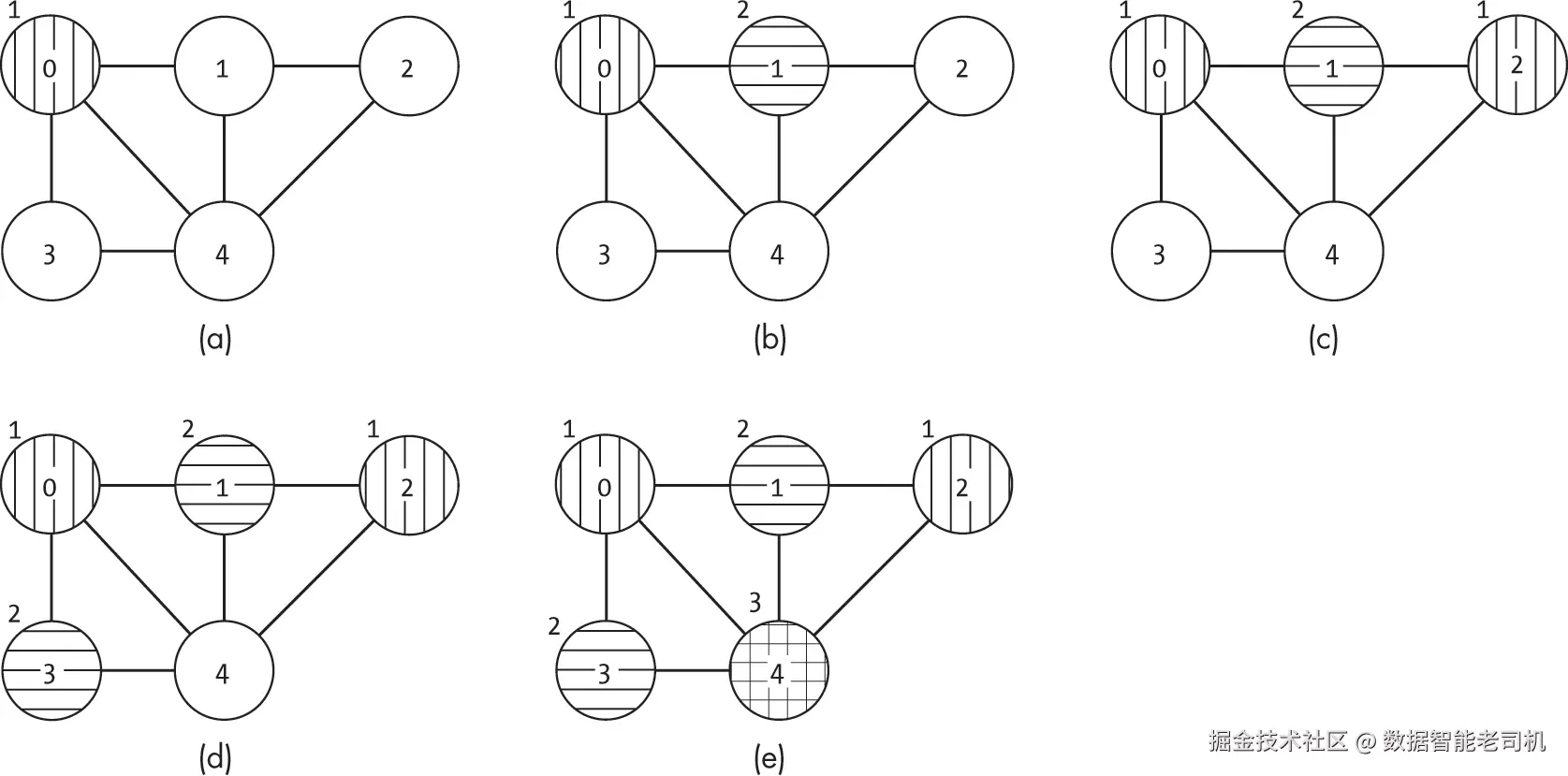
只要颜色足够，贪心算法就能为图找到一个有效的着色方案。然而，这种分配并不保证使用最少的颜色。实际上，节点分配的顺序会显著影响贪心算法需要的颜色数量。请看图 16-10，它展示了为同一张图着色的两种有效方式。

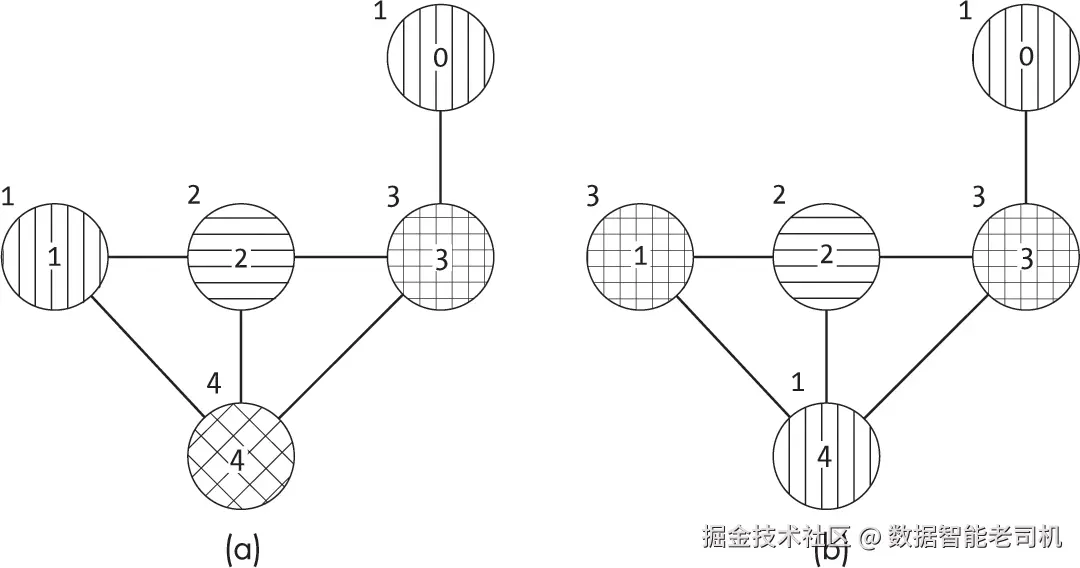
如图 16-10(a)所示，贪心算法生成的图着色方案中，由于节点 0 和节点 1 被分配了相同的颜色，因此必须在节点 4 上使用第四种颜色。相比之下，带剪枝的深度优先搜索可以找到仅需三种颜色的最优着色方案，如图 16-10(b)所示。两者的权衡在于速度与最优性的取舍。虽然贪心搜索有时会使用多于最少数量的颜色，但由于它不进行回溯，因此速度更快。

节点移除算法

另一个值得讨论的启发式算法是 IBM 的科学家团队提出的移除算法，用于在编译器中为变量分配 CPU 寄存器而避免冲突。该算法通过迭代简化问题来工作。与分配停车位的示例类似，论文作者将寄存器分配问题建模为图着色问题：节点表示变量，边表示同时使用的变量，颜色表示 CPU 的寄存器。寄存器数量由芯片架构固定为 C。算法的目标是确定是否可以找到一个使用 C 或更少颜色的有效图着色方案。

如 George Chaitin 等人在论文《Register Allocation via Coloring》中讨论的，IBM 团队提出了一种多步骤的寄存器分配方法，其中包括一个用于生成颜色分配的节点移除算法。该算法的关键洞察是，如果一个节点的边数少于 C，在为其邻居分配颜色后，可以轻松为它分配一个颜色。我们只需检查邻居的颜色，并使用 first_unused_color() 函数选择未被使用的颜色（如清单 16-3）。因此，可以初步忽略边数少于 C 的节点，专注于边数大于等于 C 的困难节点。实际上，我们可以进一步将边数少于 C 的节点及其边暂时从图中移除，同时处理剩余节点，然后在为它分配颜色时再重新添加该节点。

基于这一洞察，算法会迭代检查当前图中的节点，移除边数不超过 C 的节点及其边，并将这些节点加入栈中，以便在处理完困难节点后再次访问。随着节点和边的移除，新的节点可能降至少于 C 个邻居，也可被移除。返回时，算法会利用 first_unused_color() 为这些节点轻松找到颜色。

如果算法能够移除图中所有节点，我们就知道它找到了一个使用 C 种颜色的有效着色方案。如果搜索在栈中跟踪移除的节点，它可以弹出栈项来逆向操作、重建图，并在此过程中为节点分配颜色。

移除算法的代码采用这种两阶段方法：

def graph_color_removal(g: Graph, num_colors: int) -> bool: 
    removed: list = [False] * g.num_nodes
    node_stack: list = []
    ❶ g2 = g.make_copy()

    removed_one: bool = True
    while removed_one:
        removed_one = False
        for node in g2.nodes:
            ❷ if not removed[node.index] and node.num_edges() < num_colors:
                node_stack.append(node.index)

                ❸ all_edges: list = node.get_sorted_edge_list()
                for edge in all_edges:
                    g2.remove_edge(edge.from_node, edge.to_node)

                removed[node.index] = True
                removed_one = True

    ❹ if len(node_stack) < g.num_nodes:
        return False

    ❺ while len(node_stack) > 0:
        current: int = node_stack.pop()
        g.nodes[current].label = first_unused_color(g, current)

    return True

代码首先创建辅助数据结构。removed 数组为每个节点存储布尔值，方便快速检查节点是否仍在图中。node_stack 存储已移除节点及其移除顺序。代码还创建了图的副本 g2，以便移除边而不修改原图 ❶。

接着进入 while 循环，只要前一次迭代中至少移除一个节点（由布尔值 removed_one 跟踪），就继续循环。在循环中，遍历每个节点，检查其是否已被移除以及邻居数量 ❷。如果节点未被移除且邻居少于 C（num_colors），将节点加入 node_stack，移除所有边 ❸，并标记节点已移除。严格来说，代码只从图中移除边，节点的移除通过 removed 数组记录，从而保证 for 循环迭代的稳定性且不影响算法正确性。

如果无法将所有节点移入栈中，则说明找不到有效的颜色分配 ❹，函数返回 False。如果存在有效分配，则逐个弹出栈中的节点分配颜色 ❺。由于节点入栈时邻居少于 num_colors，因此 first_unused_color() 能在 [1, num_colors] 范围内选择一个有效颜色。

在会议策划的比喻中，移除算法就像策划者心里想着："我稍后再处理这个与会者。"每当策划者看到一个与会者的冲突少于 C，就会说："这个人不会有问题，我能为他找到桌子，先处理困难的与会者。"外人可能觉得这是拖延，但对图着色算法爱好者来说，这是关键的算法洞察。

图 16-11 展示了 C = 3 时代码第一阶段的操作。在此阶段，节点被逐个移除。while 循环的第一次迭代中，移除了三个节点。节点 2 的邻居少于 C，被加入栈中（图 16-11(b)）。随后移除节点 3（图 16-11(c)）。此时节点 4 邻居少于 C，也可移除（图 16-11(d)）。

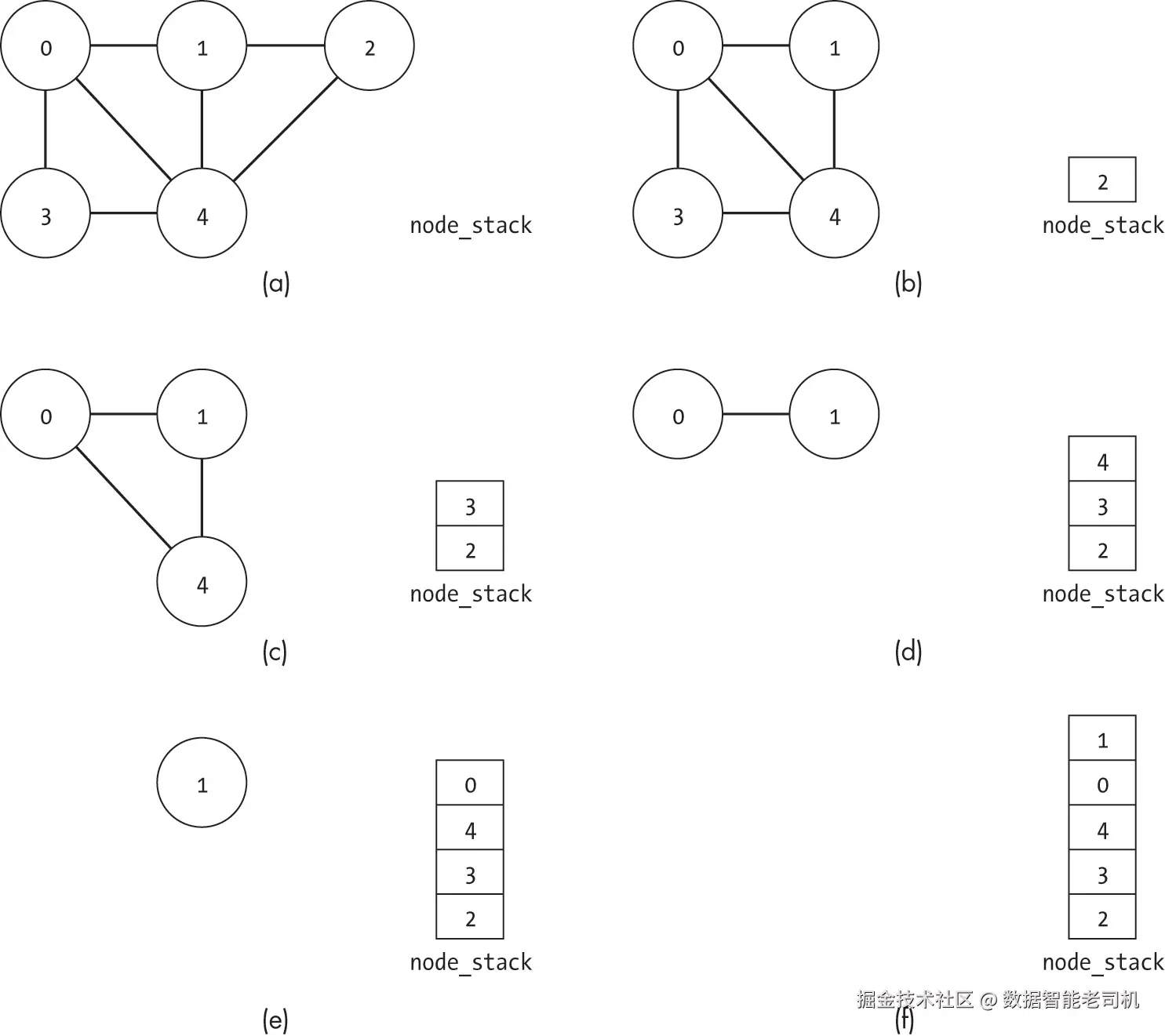
算法此时已经对图中的每个节点至少遍历了一次。由于在这一迭代中至少移除了一个节点，算法会从节点 0 重新开始检查。在图 16-11(e) 中，它移除了节点 0，该节点此时仅剩一个邻居。最后，在图 16-11(f) 中移除了节点 1。

算法的第二阶段，如图 16-12 所示，对节点进行标记并"重新添加"。算法首先从栈中弹出节点 1，并为其分配颜色 1，如图 16-12(a) 所示。在图 16-12(b) 中，算法弹出节点 0，并为节点 0 分配第一个与邻居不冲突的颜色。随后，这一过程依次继续，对节点 4、3 和 2 分别进行处理，如图 16-12(c)、16-12(d) 和 16-12(e) 所示。

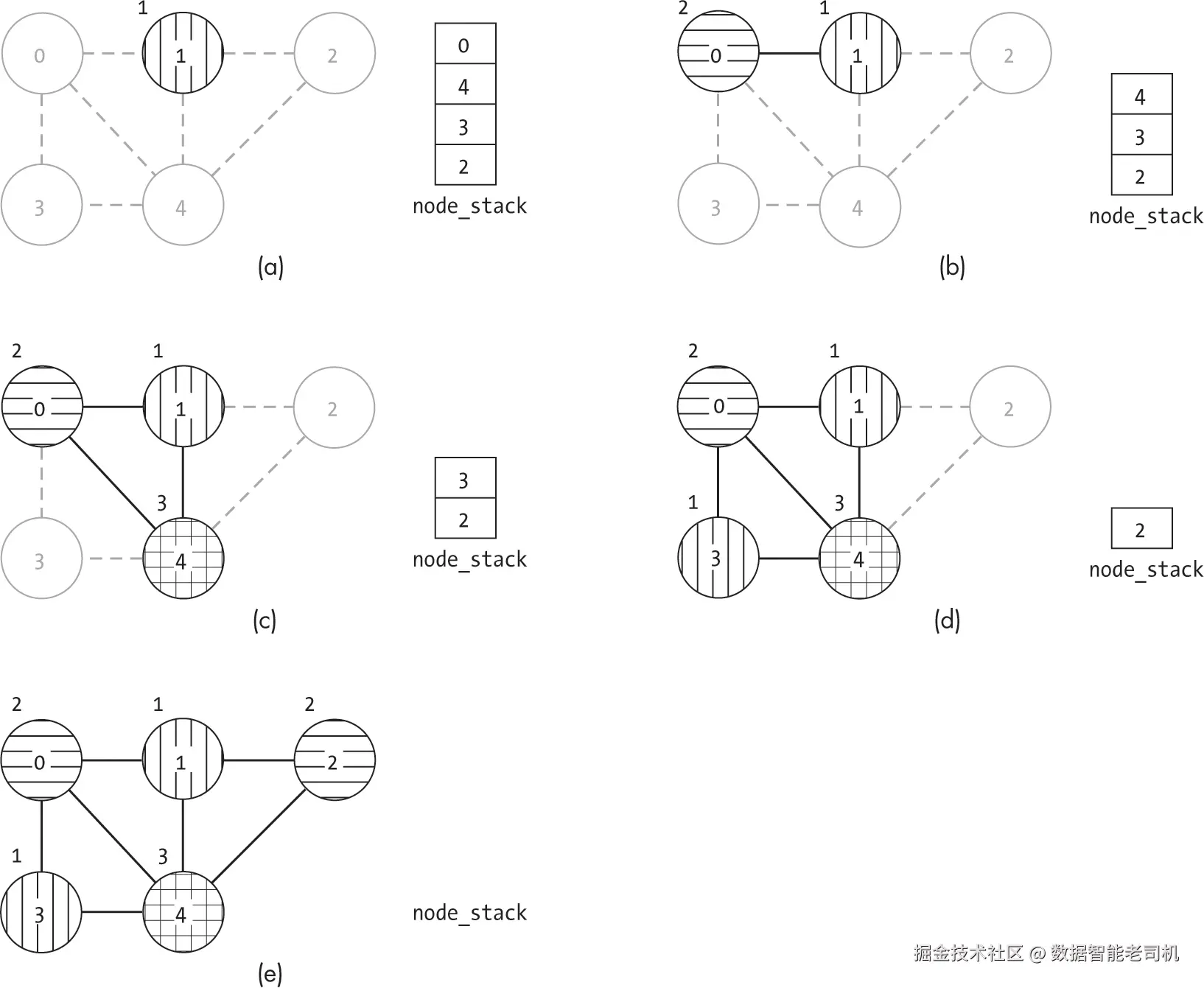
不幸的是，这种启发式方法并不能解决所有图的问题。有时，即便存在一个至少有 C 条边的互连节点簇，图着色仍然可以使用少于 C 种颜色。例如在图 16-13 中，对于 C = 3，移除算法会失败，尽管实际上存在仅需两种颜色的有效着色。由于每个节点都有三个邻居，移除算法无法移除任何节点，它陷入了僵局。

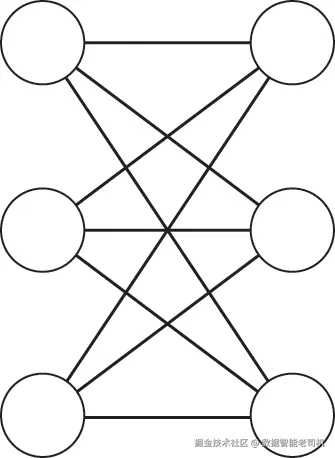
然而，很明显我们可以为图 16-13 创建一个仅使用两种颜色的有效着色方案。我们可以将左侧的所有节点分配为颜色 1，右侧的所有节点分配为颜色 2。由于边只连接左侧节点与右侧节点，因此不会产生冲突。实际上，我们可以用第 15 章介绍的二分图标记算法来解决这一特例。

为什么这很重要

将图节点分配颜色的问题在现实世界中有广泛应用，从规划魔法迷宫到分配停车位都有涉及。这个问题之所以有趣，是因为目前没有已知的算法可以高效解决所有情况。相反，我们必须依赖穷举搜索或启发式方法。这也促使人们开发出各种不同的算法，以在不同的实际场景下提供较好的性能。

在下一章中，我们将研究类似的节点分配问题，这类问题同样没有已知的高效解法。我们将探讨基于本章回溯深度优先搜索的多种分支搜索方法，同时考虑各种启发式策略以及随机算法在寻找解法中的应用。