本系列将更新FastPlanner论文内容对应代码的解读,其github的工程位置如下:
一、摘要
在本文中,提出了一种稳健高效的四旋翼运动规划系统,主要架构如下:
1.kinodynamic 路径搜索方法在离散控制空间中找到一个安全的、kinodynamic 可行且时间最短初始轨迹。
2.我们通过 B 样条优化来改善轨迹的平滑度和间隙,该优化结合了来自欧几里得距离场 (EDF) 的梯度信息和动态约束,有效地利用了 B 样条的凸包特性。
3.将最终轨迹表示为非均匀 B 样条,采用迭代时间调整方法来保证动态可行和非保守轨迹。
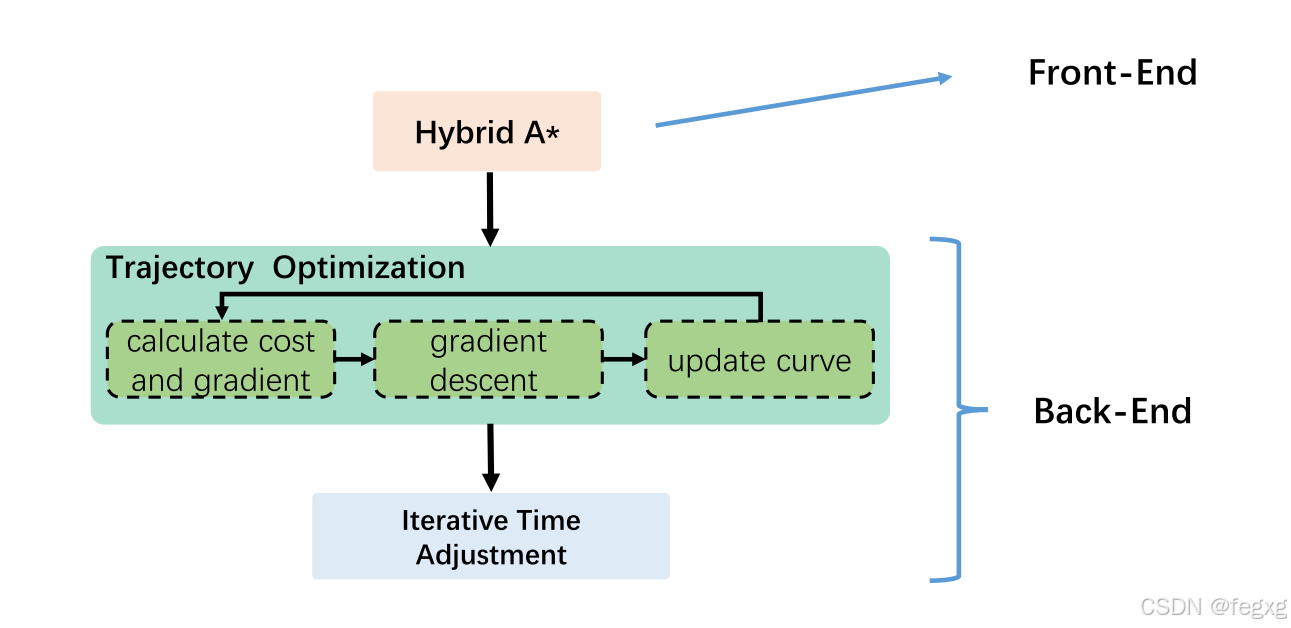
前端采用Hybrid A*算法初步搜索出一条路径,进入后端使用软约束优化得到优化好的B样条曲线,再将其表示为非均匀B样条的方式,调整控制点和时间间隔。
二、前端
1.算法架构
前端的kinodynamic path searching使用hybrid A*算法,在地图中搜索出一条安全的、动力学的可行轨迹,算法流程如下:
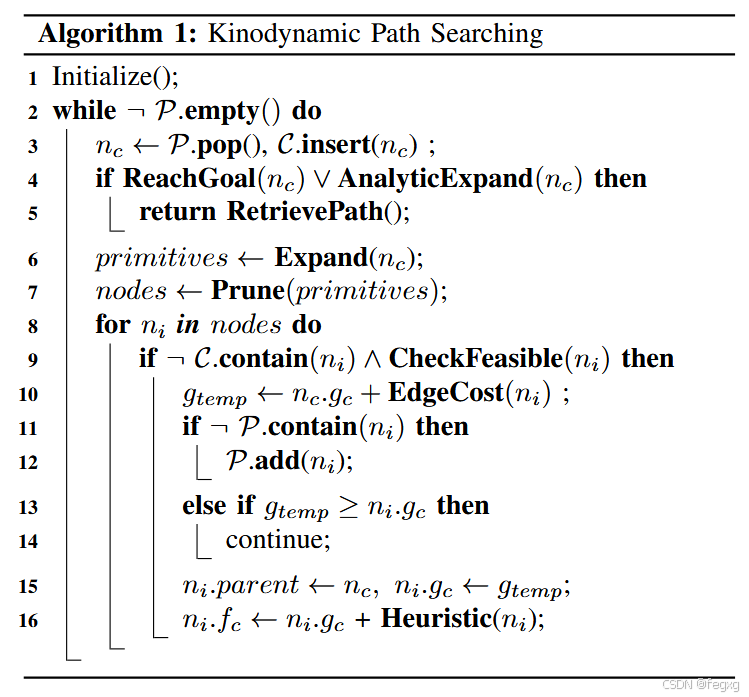
2.图搜索算法
首先我们说明图搜索算法的思路:
图搜索算法本质上是在维护一个容器,里面装着未来可能访问的节点,开始为容器里面节点数量为0,然后放入第一个节点进行循环,在循环中:
1.把容器中最符合条件的节点找到并访问弹出
2.将这个节点对周围的节点进行扩展
3.将扩展的新节点放入容器中
同时,为了防止节点被反复循环,还需要另外一个容器装载被访问的节点,后面搜索时不能再进行访问。
在这个架构下我们分析经典的基于搜索的算法:
Dijkstra算法每次弹出容器中距离源节点代价最小的节点(距离源节点的代价我们使用g来表示)。
A*算法容器的代价函数记作f,其由两个部分组成,第一个部分是g,即从源节点到当前节点累计代价,第二个部分是h,h代表启发式Heuristic代价,f=g+h。对于h的衡量有多种选择,如L2距离、曼哈顿距离等。
在原本的A*算法下,hybrid A*不同于启发式函数和动力学可行kinodynamic。在这里采用离散输入量的办法,输入量为加速度a,则位置p可以表示为:
在a的范围内进行离散采样,根据初始位置和速度可以算出该采样输入a作用下转移的新状态,由此拓展出新的节点来,并且是动力学可行的。
3.代码架构
对于这里的算法结构
首先说明其中的变量含义:
P为开集,即优先级队列,C为闭集,即已经进行扩展后的节点容器,nc为优先级队列中队首元素,nodes为拓展出的周围节点,primitives是离散输入作用的一段位移,gc为代价g,fc为总的代价f,整个流程为:
这里对应fast planner中的代码为:path_searching/src/kinodynamic_astar.cpp
cpp
int KinodynamicAstar::search(Eigen::Vector3d start_pt, Eigen::Vector3d start_v, Eigen::Vector3d start_a,
Eigen::Vector3d end_pt, Eigen::Vector3d end_v, bool init, bool dynamic, double time_start)//A*搜索
{
start_vel_ = start_v;
start_acc_ = start_a;//设置起始点的速度和加速度
PathNodePtr cur_node = path_node_pool_[0];//当前节点nc
cur_node->parent = NULL;//父节点为空
cur_node->state.head(3) = start_pt;//当前节点的位置
cur_node->state.tail(3) = start_v;//当前节点的速度
cur_node->index = posToIndex(start_pt);//将三维位置转化至栅格地图的index
cur_node->g_score = 0.0;//当前节点的gc,即从起点到当前节点的cost,这里起点为0
Eigen::VectorXd end_state(6);
Eigen::Vector3i end_index;
double time_to_goal;
end_state.head(3) = end_pt;
end_state.tail(3) = end_v;
end_index = posToIndex(end_pt);
cur_node->f_score = lambda_heu_ * estimateHeuristic(cur_node->state, end_state, time_to_goal);//计算启发式代价,初始点的fc总代价就是启发式代价,因为gc为0
cur_node->node_state = IN_OPEN_SET;//当前节点的状态,一共两种,OPEN和CLOSED,在CLOSED中的节点是已经访问过的
open_set_.push(cur_node);//OPEN加入当前节点,即优先级队列
use_node_num_ += 1;
if (dynamic)//为节点附加时间维度信息,动态搜索情况
{
time_origin_ = time_start;//记录起始时间
cur_node->time = time_start;
cur_node->time_idx = timeToIndex(time_start);//转换时间索引
expanded_nodes_.insert(cur_node->index, cur_node->time_idx, cur_node);//将 (index, time_idx) 插入到 expanded_nodes_ 中,expanded_nodes_存储已访问节点的集合
// cout << "time start: " << time_start << endl;//使用 (index, time_idx) 作为键值对,确保同一空间位置在不同时间点可以有不同的状态
}
else
expanded_nodes_.insert(cur_node->index, cur_node);//否则将用空间位置索引来记录,静态情况
PathNodePtr neighbor = NULL;
PathNodePtr terminate_node = NULL;
bool init_search = init;
const int tolerance = ceil(1 / resolution_);
while (!open_set_.empty())//主循环,优先级队列不为空
{
cur_node = open_set_.top();//弹出队首元素为当前节点nc
// Terminate?
bool reach_horizon = (cur_node->state.head(3) - start_pt).norm() >= horizon_;//接近边界
bool near_end = abs(cur_node->index(0) - end_index(0)) <= tolerance &&
abs(cur_node->index(1) - end_index(1)) <= tolerance &&
abs(cur_node->index(2) - end_index(2)) <= tolerance;//解决目标节点
if (reach_horizon || near_end)//如果某一个满足
{
terminate_node = cur_node;//当前节点为结束节点
retrievePath(terminate_node);//从结束节点开始向后倒退得到路径
if (near_end)
{
// Check whether shot traj exist
estimateHeuristic(cur_node->state, end_state, time_to_goal);//计算启发式函数,主要得到optimal_time
computeShotTraj(cur_node->state, end_state, time_to_goal);//根据这个optimal_time来计算能否直接生成一条动力学可行的路直接连接到目标点
if (init_search)//如果是初始搜索,会报错,在初始搜索阶段,如果能够直接从起点生成一条连接到目标点的轨迹(shot trajectory),通常是不合理的
ROS_ERROR("Shot in first search loop!");
}
}
if (reach_horizon)//处理各种情况
{
if (is_shot_succ_)
{
std::cout << "reach end" << std::endl;
return REACH_END;
}
else
{
std::cout << "reach horizon" << std::endl;
return REACH_HORIZON;
}
}
if (near_end)
{
if (is_shot_succ_)
{
std::cout << "reach end" << std::endl;
return REACH_END;
}
else if (cur_node->parent != NULL)
{
std::cout << "near end" << std::endl;
return NEAR_END;
}
else
{
std::cout << "no path" << std::endl;
return NO_PATH;
}
}
open_set_.pop();//弹出当前节点
cur_node->node_state = IN_CLOSE_SET;//将当前节点加入CLOSED集合,已访问过的节点集合
iter_num_ += 1;//迭代次数加1
double res = 1 / 2.0, time_res = 1 / 1.0, time_res_init = 1 / 20.0;//输入进行离散化,r取2,则对应5个离散后的输入量,
Eigen::Matrix<double, 6, 1> cur_state = cur_node->state;//当前的状态,位置和速度共6维
Eigen::Matrix<double, 6, 1> pro_state;//扩展后的节点状态
vector<PathNodePtr> tmp_expand_nodes;//临时存储当前节点扩展出的所有子节点
Eigen::Vector3d um;//代表三个维度离散的控制量
double pro_t;//表示扩展出的子节点的时间
vector<Eigen::Vector3d> inputs;
vector<double> durations;
if (init_search)
{
inputs.push_back(start_acc_);
for (double tau = time_res_init * init_max_tau_; tau <= init_max_tau_ + 1e-3;
tau += time_res_init * init_max_tau_)
durations.push_back(tau);//如果初次搜索,每次为的时间间隔三1/20,更加精细化的搜索
init_search = false;
}
else
{
for (double ax = -max_acc_; ax <= max_acc_ + 1e-3; ax += max_acc_ * res)
for (double ay = -max_acc_; ay <= max_acc_ + 1e-3; ay += max_acc_ * res)
for (double az = -max_acc_; az <= max_acc_ + 1e-3; az += max_acc_ * res)//对输入进行离散化,每次加max/r,每个离散2r+1个量,一共有(2r+1)3种组合
{
um << ax, ay, az;
inputs.push_back(um);
}
for (double tau = time_res * max_tau_; tau <= max_tau_; tau += time_res * max_tau_)//对时间进行离散化,控制输入的持续时间集合τ,有多种的时间选择(不只是t=0.5)使得新生成的路径更加多样化,不仅由离散的控制量决定,也可由离散的时间量决定
durations.push_back(tau);//这里由于time_res为1/1.0,所以durations只有一个值max_tau_
}
// cout << "cur state:" << cur_state.head(3).transpose() << endl;
for (int i = 0; i < inputs.size(); ++i)
for (int j = 0; j < durations.size(); ++j)
{
um = inputs[i];
double tau = durations[j];
stateTransit(cur_state, pro_state, um, tau);//调用状态转移函数,控制量um和时间tao作用下,得到新的状态
pro_t = cur_node->time + tau;//新状态的时间为nc当前节点的时间加上tau
Eigen::Vector3d pro_pos = pro_state.head(3);//拓展后节点的位置
// Check if in close set
Eigen::Vector3i pro_id = posToIndex(pro_pos);//拓展后节点的栅格地图的index
int pro_t_id = timeToIndex(pro_t);//拓展后节点的时间index
PathNodePtr pro_node = dynamic ? expanded_nodes_.find(pro_id, pro_t_id) : expanded_nodes_.find(pro_id);//判断是动态搜索还是静态搜索,在expanded_nodes_添加不同的键值对
if (pro_node != NULL && pro_node->node_state == IN_CLOSE_SET)//拓展出来的节点不是空节点,但其位于CLOSED集合内
{
if (init_search)
std::cout << "close" << std::endl;
continue;
}
// Check maximal velocity
Eigen::Vector3d pro_v = pro_state.tail(3);//获取拓展后节点的速度
if (fabs(pro_v(0)) > max_vel_ || fabs(pro_v(1)) > max_vel_ || fabs(pro_v(2)) > max_vel_)//检查新状态的速度是否超出最大速度限制
{
if (init_search)
std::cout << "vel" << std::endl;
continue;
}
// Check not in the same voxel
Eigen::Vector3i diff = pro_id - cur_node->index;// 空间索引差值
int diff_time = pro_t_id - cur_node->time_idx;// 时间索引差值
if (diff.norm() == 0 && ((!dynamic) || diff_time == 0))//diff.norm() == 0在三维空间索引上完全相同,两个节点位于同一个空间体素中;((!dynamic) || diff_time == 0),静态搜索(!dynamic),不检查时间维度,动态搜索检查时间维度
{
if (init_search)
std::cout << "same" << std::endl;
continue;
}
// Check safety
Eigen::Vector3d pos;
Eigen::Matrix<double, 6, 1> xt;
bool is_occ = false;
for (int k = 1; k <= check_num_; ++k)
{
double dt = tau * double(k) / double(check_num_);//将时间tau分成很多小段
stateTransit(cur_state, xt, um, dt);//每一个小段进行状态转移得到中间过程中的状态
pos = xt.head(3);//获取中间状态的位置
if (edt_environment_->sdf_map_->getInflateOccupancy(pos) == 1 )//检查中间状态是否在障碍物中,1表示在
{
is_occ = true;
break;
}
}
if (is_occ)//路径不安全
{
if (init_search)
std::cout << "safe" << std::endl;
continue;//跳过当前路径扩展
}
double time_to_goal, tmp_g_score, tmp_f_score;
tmp_g_score = (um.squaredNorm() + w_time_) * tau + cur_node->g_score;//拓展后节点的gc值是其父节点的gc值加上从当前节点到拓展节点的cost,cost计算使用ec=(u^2+w_time_)*tau
tmp_f_score = tmp_g_score + lambda_heu_ * estimateHeuristic(pro_state, end_state, time_to_goal);//拓展节点总的cost fc是gc+启发式代价
// Compare nodes expanded from the same parent
bool prune = false;//剪枝的标志位
for (int j = 0; j < tmp_expand_nodes.size(); ++j)//遍历所有拓展节点
{
PathNodePtr expand_node = tmp_expand_nodes[j];
if ((pro_id - expand_node->index).norm() == 0 && ((!dynamic) || pro_t_id == expand_node->time_idx))//检查空间上是否重复或动态模式下时间重复
{
prune = true;//标志位为true,标志需要剪枝
if (tmp_f_score < expand_node->f_score)//判断fc是否比原来的小,如果更小将说明当前的路径更优
{
expand_node->f_score = tmp_f_score;//更新fc
expand_node->g_score = tmp_g_score;//更新gc
expand_node->state = pro_state;//状态量为拓展节点的状态量位置和速度
expand_node->input = um;//节点的输入
expand_node->duration = tau;//节点的持续时间
if (dynamic)
expand_node->time = cur_node->time + tau;//pro_state
}
break;
}
}
// This node end up in a voxel different from others
if (!prune)//只有在前面的剪枝检查中未被标记为冗余节点(prune == false)时,才进一步处理新扩展的节点
{
if (pro_node == NULL)//拓展节点pro_node,如果新节点 pro_node 尚未存在
{
pro_node = path_node_pool_[use_node_num_];//创建新节点
pro_node->index = pro_id;
pro_node->state = pro_state;
pro_node->f_score = tmp_f_score;
pro_node->g_score = tmp_g_score;
pro_node->input = um;
pro_node->duration = tau;
pro_node->parent = cur_node;
pro_node->node_state = IN_OPEN_SET;
if (dynamic)
{
pro_node->time = cur_node->time + tau;
pro_node->time_idx = timeToIndex(pro_node->time);
}
open_set_.push(pro_node);//将该节点加入open_set中
if (dynamic)//记录一下节点的时间序列键值对
expanded_nodes_.insert(pro_id, pro_node->time, pro_node);
else
expanded_nodes_.insert(pro_id, pro_node);
tmp_expand_nodes.push_back(pro_node);//放在临时存储的节点
use_node_num_ += 1;//内存检查
if (use_node_num_ == allocate_num_)
{
cout << "run out of memory." << endl;
return NO_PATH;
}
}
else if (pro_node->node_state == IN_OPEN_SET)//若节点已经存在在open_set中
{
if (tmp_g_score < pro_node->g_score)//检查fc是否更小,若更优,则更新该节点的信息
{
// pro_node->index = pro_id;
pro_node->state = pro_state;
pro_node->f_score = tmp_f_score;
pro_node->g_score = tmp_g_score;
pro_node->input = um;
pro_node->duration = tau;
pro_node->parent = cur_node;
if (dynamic)
pro_node->time = cur_node->time + tau;
}
}
else
{
cout << "error type in searching: " << pro_node->node_state << endl;//新节点的状态既不是 NULL,也不是 IN_OPEN_SET
}
}
}
// init_search = false;
}
cout << "open set empty, no path!" << endl;
cout << "use node num: " << use_node_num_ << endl;
cout << "iter num: " << iter_num_ << endl;
return NO_PATH;
}4.主要函数
1.核心函数
这里核心函数是三个,Expand()、EdgeCost()和Heuristic()
1.Expand()函数
由节点nc拓展生成小轨迹primitive
轨迹为p(t),由xyz三个轴的轨迹组成,轨迹由多项式来表示:
由微分平坦性可得:
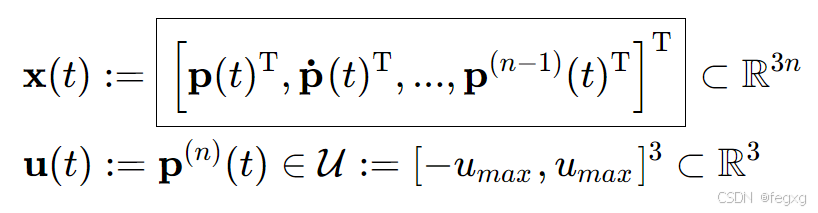
这样得到系统的状态方程为:

得到最后状态方程的解为:
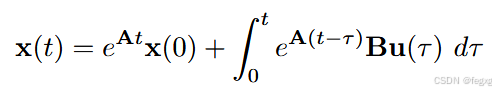
在这里输入量的范围是[−umax, umax],将其离散化为:
{−umax, − r−1 /r umax, · · · , r−1/r umax, umax},一共2r+1个离散量,三个维度一共产种组合,即动作量primitives。
对应的代码是:
cpp
double res = 1 / 2.0, time_res = 1 / 1.0, time_res_init = 1 / 20.0;//输入进行离散化,r取2,则对应5个离散后的输入量,
Eigen::Matrix<double, 6, 1> cur_state = cur_node->state;//当前的状态,位置和速度共6维
Eigen::Matrix<double, 6, 1> pro_state;//扩展后的节点状态
vector<PathNodePtr> tmp_expand_nodes;//临时存储当前节点扩展出的所有子节点
Eigen::Vector3d um;//代表三个维度离散的控制量
double pro_t;//表示扩展出的子节点的时间
vector<Eigen::Vector3d> inputs;
vector<double> durations;
if (init_search)
{
inputs.push_back(start_acc_);
for (double tau = time_res_init * init_max_tau_; tau <= init_max_tau_ + 1e-3;
tau += time_res_init * init_max_tau_)
durations.push_back(tau);//如果初次搜索,每次为的时间间隔是1/20,更加精细化的搜索
init_search = false;
}
else
{
for (double ax = -max_acc_; ax <= max_acc_ + 1e-3; ax += max_acc_ * res)
for (double ay = -max_acc_; ay <= max_acc_ + 1e-3; ay += max_acc_ * res)
for (double az = -max_acc_; az <= max_acc_ + 1e-3; az += max_acc_ * res)//对输入进行离散化,每次加max/r,每个离散2r+1个量,一共有(2r+1)3种组合
{
um << ax, ay, az;
inputs.push_back(um);
}
for (double tau = time_res * max_tau_; tau <= max_tau_; tau += time_res * max_tau_)//对时间进行离散化,控制输入的持续时间集合τ,有多种的时间选择(不只是t=0.5)使得新生成的路径更加多样化,不仅由离散的控制量决定,也可由离散的时间量决定
durations.push_back(tau);//这里由于time_res为1/1.0,所以durations只有一个值max_tau_
}在这里获得了输入量inputs和持续时间durations,这里除了开始时按照1/20来得到tau,后面的tau都是max_tai_=0.5s,动作量被记录在inputs中。
2.EdgeCost函数
如何计算每段小轨迹的代价值
每段轨迹的cost计算函数为:
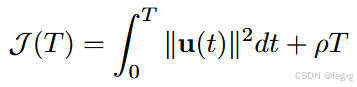
在这一小段时间τ内,认为离散输入量ud没有发生变化,所以近似其cost为
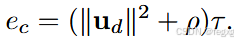
节点nc对应的gc是从源节点到当前节点的cost和的累计值,因此当前节点的gc为:
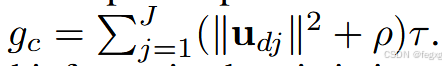
3.Heuristic函数
评估一个节点的启发代价值
这里要利用庞特里亚金极小值原理求解:
系统的状态为,
系统状态方程为
cost为:
构造哈密尔顿函数:
由极值存在的必要条件可得:
得出:
由必要条件可得:
,输入量为a,
因此将H对a求导数可得:
得到:
由a积分得到v和p,再带入T可得:
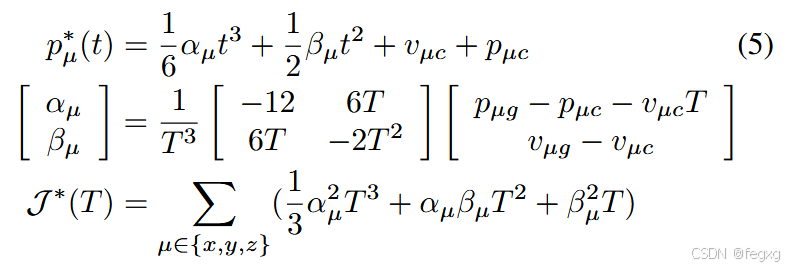
此时J*是T的函数,求出得到根Th,则
为启发式代价hc,总代价就为:
此功能在函数estimateHeuristic中实现:这里求根是用的matlab中的特征根法,传入的参数是起点和终点的位置和速度
cpp
double KinodynamicAstar::estimateHeuristic(Eigen::VectorXd x1, Eigen::VectorXd x2, double& optimal_time)//计算启发式代价,即用庞特里亚金极小值原理求解的最小代价
{//x1是起始点的位置和速度向量,共六维,x2是目标点的位置和速度向量,6维
const Vector3d dp = x2.head(3) - x1.head(3);//位置差值,即pug-puc
const Vector3d v0 = x1.segment(3, 3);//起始点的速度
const Vector3d v1 = x2.segment(3, 3);//目标点的速度
double c1 = -36 * dp.dot(dp);//这几个系数是对J(T)函数求导后的多项式系数
double c2 = 24 * (v0 + v1).dot(dp);
double c3 = -4 * (v0.dot(v0) + v0.dot(v1) + v1.dot(v1));
double c4 = 0;
double c5 = w_time_;//即公式中的p(rou)
std::vector<double> ts = quartic(c5, c4, c3, c2, c1);//特征根法求解导数方程的解,得到根T,这里是一个数组ts
double v_max = max_vel_ * 0.5;
double t_bar = (x1.head(3) - x2.head(3)).lpNorm<Infinity>() / v_max;
ts.push_back(t_bar);//估算一个最小值,用dp中最大的一个维度除以最大速度的一半,用于后续进行比较
double cost = 100000000;//记录最小的cost,初始赋值为一个很大的数
double t_d = t_bar;//用于记录最小cost对应的根
for (auto t : ts)//便利所有的解
{
if (t < t_bar)
continue;
double c = -c1 / (3 * t * t * t) - c2 / (2 * t * t) - c3 / t + w_time_ * t;//J(T)函数,计算cost
if (c < cost)
{
cost = c;
t_d = t;
}
}
optimal_time = t_d;//容器optimal_time中记录了最优的时间Th
return 1.0 * (1 + tie_breaker_) * cost;//加入一个微小的偏移量,用于打破相同代价的情况下的平局
}2.其他函数
同时,还有以下几个函数值得注意:
1.AnalyticExpand()
由于离散化的 control input,很难在 goal state 中有一个 primitive end,即我们在nc点通过离散输入的作用,下一个状态刚好到达了goal点。为了补偿它并加快搜索速度,我们引入了一个分析扩展方案。
主要思路是,我们弹出节点nc,用之前相同的方法算一条从当前点nc到目标点xg的路径,如果这条路径是安全的(没有障碍物碰撞)并且是动力学可行的,那么我们就提前停止搜索。
对应的代码是这一段:
cpp
// Terminate?
bool reach_horizon = (cur_node->state.head(3) - start_pt).norm() >= horizon_;//接近边界
bool near_end = abs(cur_node->index(0) - end_index(0)) <= tolerance &&
abs(cur_node->index(1) - end_index(1)) <= tolerance &&
abs(cur_node->index(2) - end_index(2)) <= tolerance;//解决目标节点
if (reach_horizon || near_end)//如果某一个满足
{
terminate_node = cur_node;//当前节点为结束节点
retrievePath(terminate_node);//从结束节点开始向后倒退得到路径
if (near_end)
{
// Check whether shot traj exist
estimateHeuristic(cur_node->state, end_state, time_to_goal);//计算启发式函数,主要得到optimal_time
computeShotTraj(cur_node->state, end_state, time_to_goal);//根据这个optimal_time来计算能否直接生成一条动力学可行的路直接连接到目标点
if (init_search)//如果是初始搜索,会报错,在初始搜索阶段,如果能够直接从起点生成一条连接到目标点的轨迹(shot trajectory),通常是不合理的
ROS_ERROR("Shot in first search loop!");
}
}
if (reach_horizon)//处理各种情况
{
if (is_shot_succ_)
{
std::cout << "reach end" << std::endl;
return REACH_END;
}
else
{
std::cout << "reach horizon" << std::endl;
return REACH_HORIZON;
}
}
if (near_end)
{
if (is_shot_succ_)
{
std::cout << "reach end" << std::endl;
return REACH_END;
}
else if (cur_node->parent != NULL)
{
std::cout << "near end" << std::endl;
return NEAR_END;
}
else
{
std::cout << "no path" << std::endl;
return NO_PATH;
}
}首先检查是否接近目标点,使用标识位near_end,计算启发式代价得到最优时间Th,通过这个Th计算从当前点到终点直接连线的路径,具体是在函数computeShort内完成的。
cpp
bool KinodynamicAstar::computeShotTraj(Eigen::VectorXd state1, Eigen::VectorXd state2, double time_to_goal)//计算一个从当前节点到目标节点的直接路径
{
/* ---------- get coefficient ---------- */
const Vector3d p0 = state1.head(3);
const Vector3d dp = state2.head(3) - p0;
const Vector3d v0 = state1.segment(3, 3);
const Vector3d v1 = state2.segment(3, 3);
const Vector3d dv = v1 - v0;
double t_d = time_to_goal;
MatrixXd coef(3, 4);//三维轨迹的多项式系数存储为矩阵
end_vel_ = v1;
Vector3d a = 1.0 / 6.0 * (-12.0 / (t_d * t_d * t_d) * (dp - v0 * t_d) + 6 / (t_d * t_d) * dv);
Vector3d b = 0.5 * (6.0 / (t_d * t_d) * (dp - v0 * t_d) - 2 / t_d * dv);
Vector3d c = v0;
Vector3d d = p0;
// 1/6 * alpha * t^3 + 1/2 * beta * t^2 + v0 使用三次多项式描述轨迹p(t)
// a*t^3 + b*t^2 + v0*t + p0 a,b,c,d多项是
coef.col(3) = a, coef.col(2) = b, coef.col(1) = c, coef.col(0) = d;//对应每一列是ax,ay,az;bx,by,bz等
Vector3d coord, vel, acc;
VectorXd poly1d, t, polyv, polya;
Vector3i index;
Eigen::MatrixXd Tm(4, 4);
Tm << 0, 1, 0, 0, 0, 0, 2, 0, 0, 0, 0, 3, 0, 0, 0, 0;//用于求导数的
/* ---------- forward checking of trajectory ---------- */
double t_delta = t_d / 10;//td是optimal_time,将其分为一段一段,对每个时间点t,计算对应的轨迹位置、速度、加速度,并进行检查
for (double time = t_delta; time <= t_d; time += t_delta)
{
t = VectorXd::Zero(4);//t是一个多项式,表示[1,t,t2,t3]多项式
for (int j = 0; j < 4; j++)
t(j) = pow(time, j);
for (int dim = 0; dim < 3; dim++)
{
poly1d = coef.row(dim);//从0-2行的系数,对应x,y,z
coord(dim) = poly1d.dot(t);//计算位置
vel(dim) = (Tm * poly1d).dot(t);//计算速度
acc(dim) = (Tm * Tm * poly1d).dot(t);//计算加速度
if (fabs(vel(dim)) > max_vel_ || fabs(acc(dim)) > max_acc_)//检查速度和加速度是否超限
{
// cout << "vel:" << vel(dim) << ", acc:" << acc(dim) << endl;
// return false;
}
}
if (coord(0) < origin_(0) || coord(0) >= map_size_3d_(0) || coord(1) < origin_(1) || coord(1) >= map_size_3d_(1) ||
coord(2) < origin_(2) || coord(2) >= map_size_3d_(2))//检查轨迹是否超出地图边界
{
return false;
}
// if (edt_environment_->evaluateCoarseEDT(coord, -1.0) <= margin_) {
// return false;
// }
if (edt_environment_->sdf_map_->getInflateOccupancy(coord) == 1)//检查轨迹位置是否碰撞障碍物,碰到障碍物则无法生成
{
return false;
}
}
//轨迹生成结果
coef_shot_ = coef;//系数
t_shot_ = t_d;//最优时间
is_shot_succ_ = true;//能否生成直接连接轨迹标志位
return true;
}传入的参数是起点和终点的状态,包括位置和速度,同时传入轨迹的时间,是之前利用极小值原理计算出来的最优时间。
系数存放在coef内,三列对应xyz三个轴,4代表多项式系数,对应多项式为:
t从t_delta开始每次增加t_delta,在每个时间点检查速度、加速度是否动力学可行,同时检查位置是否在地图范围内和是否有障碍物,最终返回生成轨迹成功与否。
2.Prune()函数
计算出根据动作量primitives拓展出来的节点nodes,并进行剪枝操作留下复合要求的节点。
对应代码为:
cpp
// Check safety
Eigen::Vector3d pos;
Eigen::Matrix<double, 6, 1> xt;
bool is_occ = false;
for (int k = 1; k <= check_num_; ++k)
{
double dt = tau * double(k) / double(check_num_);//将时间tau分成很多小段
stateTransit(cur_state, xt, um, dt);//每一个小段进行状态转移得到中间过程中的状态
pos = xt.head(3);//获取中间状态的位置
if (edt_environment_->sdf_map_->getInflateOccupancy(pos) == 1 )//检查中间状态是否在障碍物中,1表示在
{
is_occ = true;
break;
}
}
if (is_occ)//路径不安全
{
if (init_search)
std::cout << "safe" << std::endl;
continue;//跳过当前路径扩展
}
double time_to_goal, tmp_g_score, tmp_f_score;
tmp_g_score = (um.squaredNorm() + w_time_) * tau + cur_node->g_score;//拓展后节点的gc值是其父节点的gc值加上从当前节点到拓展节点的cost,cost计算使用ec=(u^2+w_time_)*tau
tmp_f_score = tmp_g_score + lambda_heu_ * estimateHeuristic(pro_state, end_state, time_to_goal);//拓展节点总的cost fc是gc+启发式代价
// Compare nodes expanded from the same parent
bool prune = false;//剪枝的标志位
for (int j = 0; j < tmp_expand_nodes.size(); ++j)//遍历所有拓展节点
{
PathNodePtr expand_node = tmp_expand_nodes[j];
if ((pro_id - expand_node->index).norm() == 0 && ((!dynamic) || pro_t_id == expand_node->time_idx))//检查空间上是否重复或动态模式下时间重复
{
prune = true;//标志位为true,标志需要剪枝
if (tmp_f_score < expand_node->f_score)//判断fc是否比原来的小,如果更小将说明当前的路径更优
{
expand_node->f_score = tmp_f_score;//更新fc
expand_node->g_score = tmp_g_score;//更新gc
expand_node->state = pro_state;//状态量为拓展节点的状态量位置和速度
expand_node->input = um;//节点的输入
expand_node->duration = tau;//节点的持续时间
if (dynamic)
expand_node->time = cur_node->time + tau;//pro_state
}
break;
}
}首先对通过primitives到目标点的路径进行障碍物检查,这里用的是采样的方法,在路径中间一小段时间进行采样,检查其是否位于障碍物内。
对通过安全性检查的节点进行剪枝操作,如果检测到当前扩展的节点与已有节点相同(位置和时间),并且当前路径的总代价更小,则更新节点的 f_score、g_score、state、input 和 duration 等信息并继续。
3.扩展新的节点
接着我们来看如何进行路径扩展 中的新节点创建和更新
对应代码如下:
cpp
// This node end up in a voxel different from others
if (!prune)//只有在前面的剪枝检查中未被标记为冗余节点(prune == false)时,才进一步处理新扩展的节点
{
if (pro_node == NULL)//拓展节点pro_node,如果新节点 pro_node 尚未存在
{
pro_node = path_node_pool_[use_node_num_];//创建新节点
pro_node->index = pro_id;
pro_node->state = pro_state;
pro_node->f_score = tmp_f_score;
pro_node->g_score = tmp_g_score;
pro_node->input = um;
pro_node->duration = tau;
pro_node->parent = cur_node;
pro_node->node_state = IN_OPEN_SET;
if (dynamic)
{
pro_node->time = cur_node->time + tau;
pro_node->time_idx = timeToIndex(pro_node->time);
}
open_set_.push(pro_node);//将该节点加入open_set中
if (dynamic)//记录一下节点的时间序列键值对
expanded_nodes_.insert(pro_id, pro_node->time, pro_node);
else
expanded_nodes_.insert(pro_id, pro_node);
tmp_expand_nodes.push_back(pro_node);//放在临时存储的节点
use_node_num_ += 1;//内存检查
if (use_node_num_ == allocate_num_)
{
cout << "run out of memory." << endl;
return NO_PATH;
}
}
else if (pro_node->node_state == IN_OPEN_SET)//若节点已经存在在open_set中
{
if (tmp_g_score < pro_node->g_score)//检查fc是否更小,若更优,则更新该节点的信息
{
// pro_node->index = pro_id;
pro_node->state = pro_state;
pro_node->f_score = tmp_f_score;
pro_node->g_score = tmp_g_score;
pro_node->input = um;
pro_node->duration = tau;
pro_node->parent = cur_node;
if (dynamic)
pro_node->time = cur_node->time + tau;
}
}
else
{
cout << "error type in searching: " << pro_node->node_state << endl;//新节点的状态既不是 NULL,也不是 IN_OPEN_SET
}
}其代码的架构为:
cpp
if (!prune)
{
if (pro_node == NULL)
{
// 创建新节点,表示如果当前扩展的节点还不存在(即是一个新节点),则需要创建一个新的节点。
}
else if (pro_node->node_state == IN_OPEN_SET)
{
// 如果节点已存在并在OPEN集合中,检查路径是否更优
}
else
{
std::cout << "error type in searching: " << pro_node->node_state << std::endl;
}
}第一段代码将扩展的节点加入到OPEN集合中
核心在于第二段,从OPEN集合中找到一个fc最优的节点,将当前节点设置为该节点的父节点,并更新其各个代价信息等。
对应这一段功能
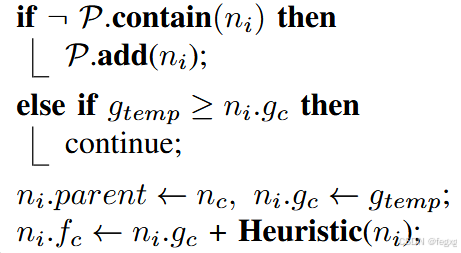
总体的代码流程如下:
cpp
1. 初始化
输入:起始点位置、速度、加速度,目标点位置、速度。
设置起始节点:
设定起始点的 位置、速度、加速度。
计算起始节点的 代价(g_score) 和 启发式代价(f_score),并加入 开放集(open_set)。
2. 主循环:处理开放集中的节点
判断开放集是否为空:
如果为空,算法结束,返回 NO_PATH。
如果非空,弹出 代价最小的节点 cur_node。
3. 检查终止条件
接近边界:检查当前节点是否接近预定的边界(例如搜索区域的最大范围),若是,设置标志为 reach_horizon。
接近目标节点:检查当前节点是否接近目标节点,若是,设置标志为 near_end。
如果满足终止条件:
从目标节点开始倒退,找到路径并返回 REACH_END。
如果接近边界但未到达目标,返回 REACH_HORIZON。
4. 路径扩展
对于每个可能的 控制输入 和 持续时间,计算新的状态(位置、速度等)。
计算扩展节点的代价:计算从当前节点到扩展节点的代价(g_score 和 f_score)。
5. 剪枝操作
检查扩展的节点是否已经处理过:
如果扩展的节点已经在 CLOSED 集合 中,跳过该节点。
如果扩展的节点已经在 OPEN 集合 中,并且当前路径代价更优,则更新该节点。
6. 安全性检查
将路径分成小段,检查每个小段是否碰到障碍物:
如果路径中的任意小段与障碍物碰撞,则标记该路径为 不安全,跳过该路径扩展。
7. 节点更新
新节点创建:如果扩展的节点是新的,创建该节点并加入 OPEN 集合,同时更新节点的状态和代价。
更新已存在的节点:如果节点已经在 OPEN 集合 中,并且当前路径更优,则更新该节点的信息(状态、代价等)。
8. 内存管理
检查节点是否超出预定的最大数量。如果超出,则返回 NO_PATH,表示内存不足。
9. 返回结果
如果找到路径,返回 REACH_END。
如果没有路径可扩展,返回 NO_PATH。
结束条件:
终止条件检查、路径扩展、剪枝、安全性检查等操作反复进行,直到找到路径或者无法找到路径为止。