【C++篇】树影摇曳，旋转无声：探寻AVL树的平衡之道

Trouvaille ~2025-02-22 17:07

文章目录

    • 从结构到操作：手撕AVL树的实现
    • 一、AVL树介绍
      • [1.1 什么是AVL树](#1.1 什么是AVL树)
      • [1.2 平衡因子的定义](#1.2 平衡因子的定义)
      • [1.3 平衡的意义](#1.3 平衡的意义)
      • [1.4 AVL树的操作](#1.4 AVL树的操作)
    • 二、AVL树的节点结构
      • [2.1 节点结构的定义：](#2.1 节点结构的定义：)
    • 三、插入操作
      • [3.1 插入操作概述](#3.1 插入操作概述)
      • [3.2 步骤1：按二叉查找树规则插入节点](#3.2 步骤1：按二叉查找树规则插入节点)
      • [3.3 步骤2：更新平衡因子](#3.3 步骤2：更新平衡因子)
      • [3.4 步骤3：旋转操作详解](#3.4 步骤3：旋转操作详解)
        • [3.4.1 右单旋](#3.4.1 右单旋)
        • [3.4.2 左单旋](#3.4.2 左单旋)
        • [3.4.3 左右双旋](#3.4.3 左右双旋)
        • [3.4.4 右左双旋](#3.4.4 右左双旋)
    • 四、其他操作
      • [4.1 查找操作 (`Find`)](#4.1 查找操作 (Find))
      • [4.2 计算树的高度 (`Height`)](#4.2 计算树的高度 (Height))
      • [4.3 计算节点数量 (`Size`)](#4.3 计算节点数量 (Size))
      • [4.4 树是否平衡 (`IsBalanceTree`)](#4.4 树是否平衡 (IsBalanceTree))
    • 五、性能分析与测试
      • [5.1 性能分析](#5.1 性能分析)
      • [5.2 测试代码](#5.2 测试代码)
    • 六、全部代码
    • 七、总结与展望

从结构到操作：手撕AVL树的实现

💬 欢迎讨论：如果你在阅读过程中有任何疑问或想要进一步探讨的内容，欢迎在评论区留言！我们一起学习、一起成长。

👍 点赞、收藏与分享：如果你觉得这篇文章对你有帮助，记得点赞、收藏并分享给更多的朋友！

🚀 逐步实现AVL树：本篇文章将带你一步一步实现一个自平衡的二叉查找树------AVL树，从最基本的节点结构开始，逐步实现插入、查找等操作，并确保每个步骤都详细讲解。

一、AVL树介绍

1.1 什么是AVL树

AVL树 是一种自平衡的二叉查找树（BST），由G.M. Adelson-Velsky 和E.M. Landis于1962年提出。AVL树的核心特点是它保证树的每个节点的左右子树的高度差（平衡因子）不超过1，从而保证了AVL树在插入、删除和查找操作时的时间复杂度始终为O(log N)。

1.2 平衡因子的定义

每个节点都有一个平衡因子 （_bf），它表示节点左子树的高度减去右子树的高度：
平衡因子 = 左子树的高度 − 右子树的高度 \text{平衡因子} = \text{左子树的高度} - \text{右子树的高度} 平衡因子=左子树的高度−右子树的高度

  • 如果平衡因子为 0，表示左右子树的高度相等。
  • 如果平衡因子为 1，表示左子树比右子树高1。
  • 如果平衡因子为 -1，表示右子树比左子树高1。

1.3 平衡的意义

AVL树的自平衡特性确保了其查询、插入和删除操作的最坏时间复杂度为O(log N)，避免了普通二叉查找树的退化（比如变成链表）。因此，AVL树非常适用于需要频繁插入和删除操作的场景。

1.4 AVL树的操作

AVL树的主要操作有：

  • 插入操作：在树中插入节点，并在插入后调整平衡因子。如果平衡因子为2或-2，执行旋转操作恢复平衡。
  • 删除操作：删除节点，并且在删除节点后，可能需要调整树的结构以保持平衡。由于AVL树的删除操作涉及复杂的旋转和调整，因此在本文中我们不会详细讲解该操作。如果你希望深入了解，可以参考《算法导论》中的相关章节来获取详细内容。
  • 查找操作：通过比较节点值来查找特定的元素。
  • 旋转操作：当树失衡时，使用旋转来恢复平衡，常见的旋转有左旋、右旋、左右旋和右左旋。

二、AVL树的节点结构

在实现AVL树之前，首先要定义节点结构。每个节点存储以下信息：

  • 键值对 （_kv）：存储数据（pair<K, V>）。
  • 左右子树指针 （_left, _right）：指向左右子树。
  • 父节点指针 （_parent）：指向父节点。
  • 平衡因子 （_bf）：用于标识该节点的左右子树的高度差。

2.1 节点结构的定义：

cpp 复制代码 
template<class K, class V>
struct AVLTreeNode
{
    pair<K, V> _kv;               // 存储键值对
    AVLTreeNode<K, V>* _left;      // 左子树指针
    AVLTreeNode<K, V>* _right;     // 右子树指针
    AVLTreeNode<K, V>* _parent;    // 父节点指针
    int _bf;                       // 平衡因子

    // 构造函数
    AVLTreeNode(const pair<K, V>& kv)
        :_kv(kv), _left(nullptr), _right(nullptr), _parent(nullptr), _bf(0)
    {}
};

三、插入操作

3.1 插入操作概述

AVL树的插入操作包括三步：

  1. 按二叉查找树规则插入节点；
  2. 更新每个节点的平衡因子；
  3. 如果需要，进行旋转操作来恢复树的平衡。
cpp 复制代码 
bool Insert(const pair<K, V>& kv);

3.2 步骤1：按二叉查找树规则插入节点

在插入节点时，我们根据值的大小，递归地找到插入位置，并在该位置插入新节点：

cpp 复制代码 
if (_root == nullptr) {
    _root = new Node(kv);  // 如果树为空，直接插入根节点
    return true;
}

Node* parent = nullptr;
Node* cur = _root;
while (cur) {
    if (cur->_kv.first < kv.first) {
        parent = cur;
        cur = cur->_right;  // 在右子树中查找插入位置
    } else if (cur->_kv.first > kv.first) {
        parent = cur;
        cur = cur->_left;  // 在左子树中查找插入位置
    } else {
        return false;  // 如果节点已存在，不插入
    }
}

cur = new Node(kv);
if (parent->_kv.first < kv.first)
{
	parent->_right = cur;
}
else
{
	parent->_left = cur;
}
//更新插入节点的_parent
cur->_parent = parent;

3.3 步骤2：更新平衡因子

插入节点后，我们从新插入的节点开始，逐步更新路径上每个节点的平衡因子。插入时会对父节点的平衡因子进行调整：

cpp 复制代码 
while (parent)
{
	if (cur == parent->_left)
	{
		parent->_bf++;
	}
	else
	{
		parent->_bf--;
	}

	if (parent->_bf == 0)
	{
		break;
	}
	else if (parent->_bf == 1 || parent->_bf == -1)
	{
		cur = parent;
		parent = cur->_parent;
	}
	else if (parent->_bf == 2 || parent->_bf == -2)
	{
		//旋转
		if (parent->_bf == 2 && cur->_bf == 1)
		{
			RotateR(parent);
		}
		else if (parent->_bf == -2 && cur->_bf == -1)
		{
			RotateL(parent);
		}
		else if (parent->_bf == 2 && cur->_bf == -1)
		{
			RotateLR(parent);
		}
		else if (parent->_bf == -2 && cur->_bf == 1)
		{
			RotateRL(parent);
		}
		else
			assert(false);
		break;
	}
	else
	{
		assert(false);
	}
}
return true;

3.4 步骤3：旋转操作详解

如果某个节点的平衡因子为2或-2，表示该节点不平衡。我们需要通过旋转操作来恢复平衡。旋转操作有四种：

  1. 右单旋（RotateR）
  2. 左单旋（RotateL）
  3. 左右双旋（RotateLR）
  4. 右左双旋（RotateRL）
3.4.1 右单旋

右单旋适用于当左子树较高时，执行旋转操作来恢复平衡。


cpp 复制代码 
void RotateR(Node* parent) {
    Node* subL = parent->_left;
    Node* subLR = subL->_right;
    Node* ppNode = parent->_parent;

    parent->_left = subLR;
    if (subLR) {
        subLR->_parent = parent;
    }

    subL->_right = parent;
    parent->_parent = subL;

    if (parent == _root) {
        subL->_parent = nullptr;
        _root = subL;
    } else {
        subL->_parent = ppNode;
        if (parent == ppNode->_right)
            ppNode->_right = subL;
        else
            ppNode->_left = subL;
    }

    parent->_bf = 0;
    subL->_bf = 0;
}
3.4.2 左单旋

左单旋适用于当右子树较高时，执行旋转操作来恢复平衡。


cpp 复制代码 
void RotateL(Node* parent) {
    Node* subR = parent->_right;
    Node* ppNode = parent->_parent;
    Node* subRL = subR->_left;

    parent->_right = subRL;
    parent->_parent = subR;
    if (subRL) {
        subRL->_parent = parent;
    }

    subR->_left = parent;
    if (parent == _root) {
        _root = subR;
        subR->_parent = nullptr;
    } else {
        subR->_parent = ppNode;
        if (parent == ppNode->_right)
            ppNode->_right = subR;
        else
            ppNode->_left = subR;
    }

    parent->_bf = 0;
    subR->_bf = 0;
}
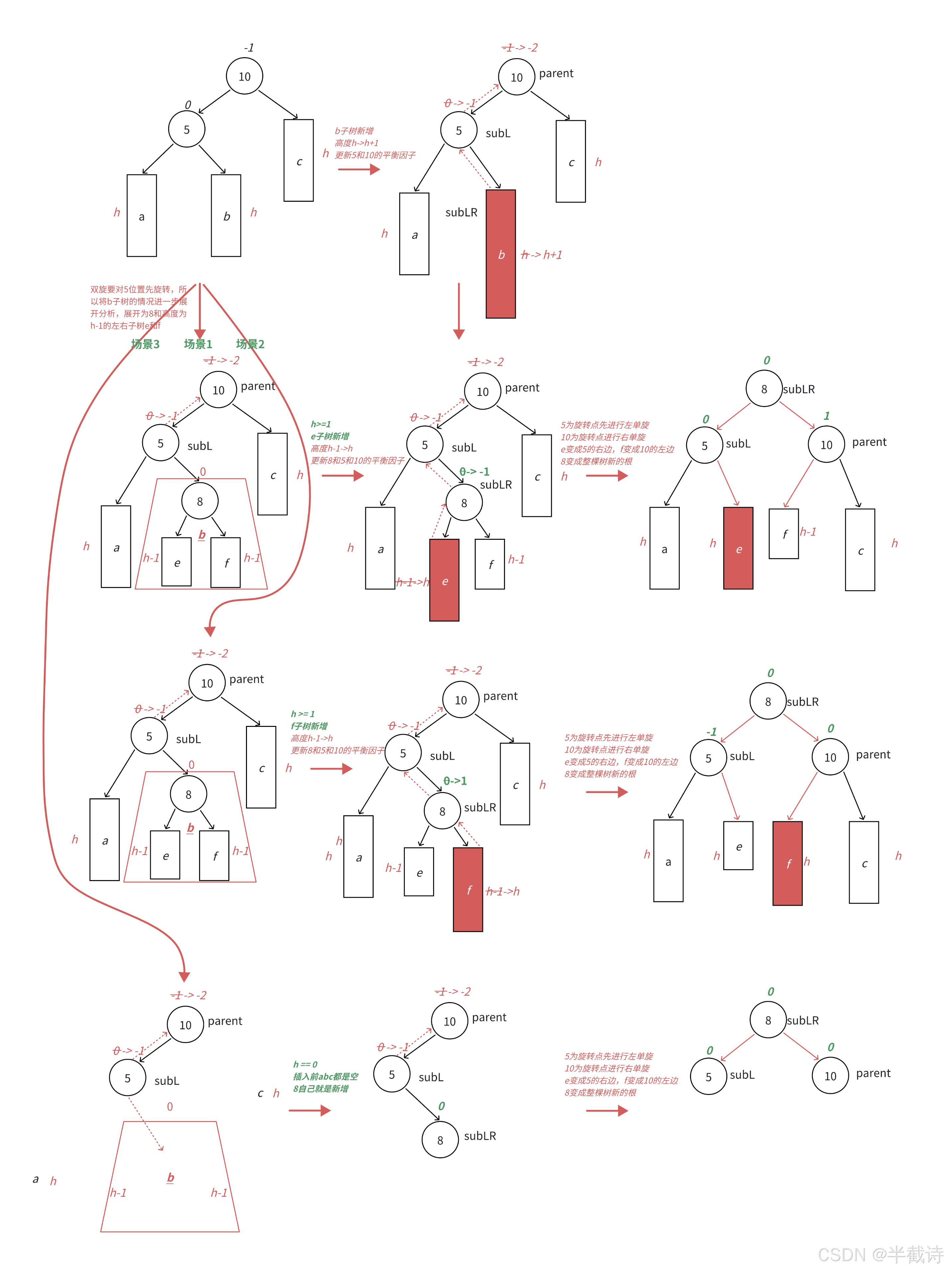
3.4.3 左右双旋


当左子树的右子树较高时，首先进行左旋，再进行右旋，恢复平衡。

cpp 复制代码 
void RotateLR(Node* parent) {
    Node* subL = parent->_left;
    Node* subLR = subL->_right;
    int bf = subLR->_bf;

    RotateL(subL);  // 左旋
    RotateR(parent);  // 右旋

    if (bf == 1) {
        subLR->_bf = 0;
        subL->_bf = 0;
        parent->_bf = -1;
    } else if (bf == -1) {
        subLR->_bf = 0;
        subL->_bf = 1;
        parent->_bf = 0;
    } else if (bf == 0) {
        subL->_bf = subLR->_bf = parent->_bf = 0;
    }
}
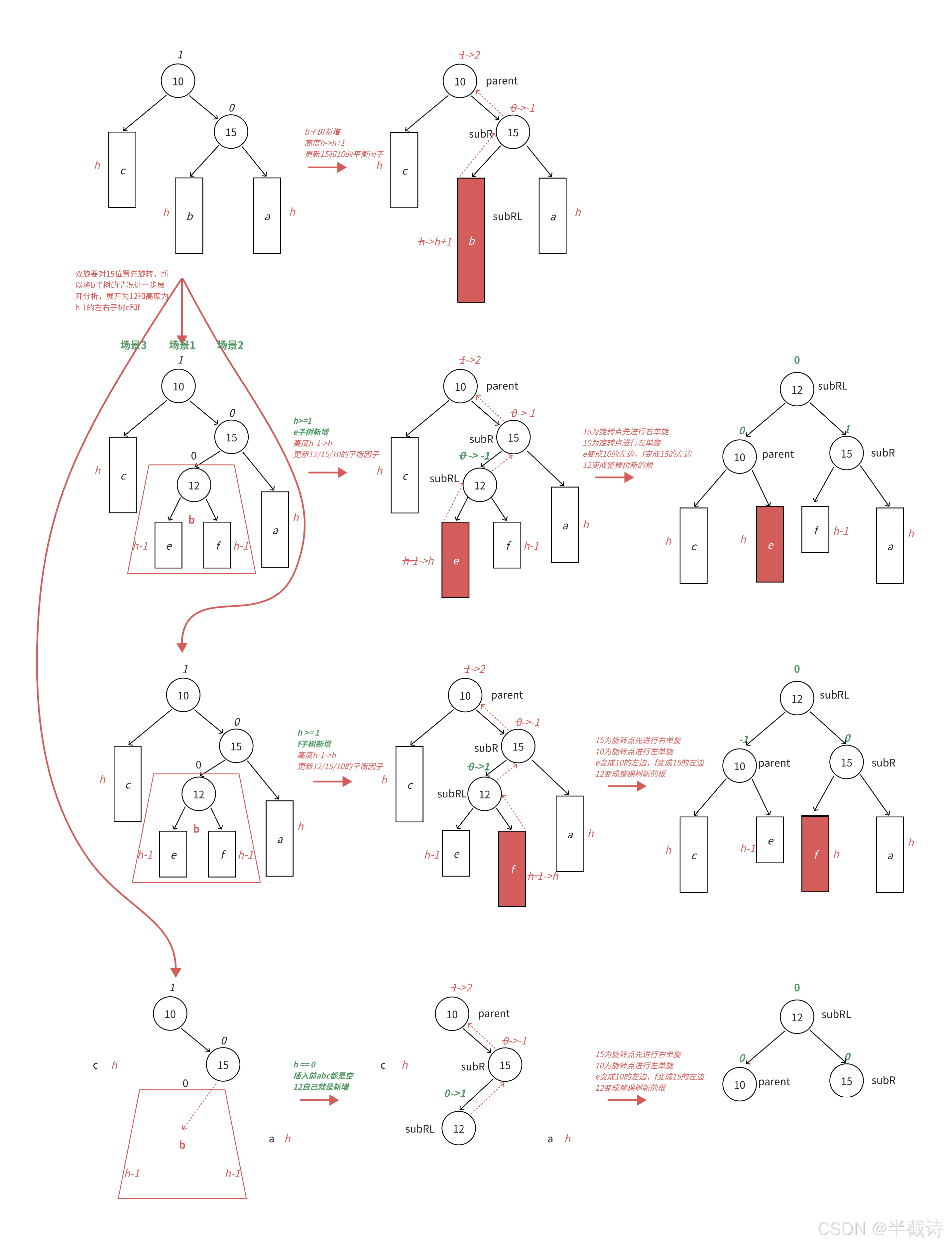
3.4.4 右左双旋

当右子树的左子树较高时，首先进行右旋，再进行左旋，恢复平衡。

cpp 复制代码 
void RotateRL(Node* parent) {
    Node* subR = parent->_right;
    Node* subRL = subR->_left;
    int bf = subRL->_bf;

    RotateR(subR);  // 右旋
    RotateL(parent);  // 左旋

    if (bf == 0) {
        parent->_bf = subR->_bf = subRL->_bf = 0;
    } else if (bf == 1) {
        subRL->_bf = 0;
        parent->_bf = 0;
        subR->_bf = -1;
    } else if (bf == -1) {
        subRL->_bf = 0;
        parent->_bf = 1;
        subR->_bf = 0;
    }
}

总结：找失衡原因，决定如何旋转

  • 左子树的左子树高：进行R
  • 右子树的右子树高：进行L
  • 左子树的右子树高：进行LR
  • 右子树的左子树高：进行RL

四、其他操作

4.1 查找操作 (Find)

查找操作与普通的二叉查找树类似。通过不断比较当前节点的键值和目标值，沿树的路径查找目标节点。

cpp 复制代码 
Node* Find(const K& key) {
    Node* cur = _root;
    while (cur) {
        if (cur->_kv.first < key)
            cur = cur->_right;  // 目标键值比当前节点大，往右子树查找
        else if (cur->_kv.first > key)
            cur = cur->_left;   // 目标键值比当前节点小，往左子树查找
        else
            return cur;  // 找到目标节点，返回该节点
    }
    return nullptr;  // 如果没有找到，返回空
}

该方法的时间复杂度为 O(log N)，因为AVL树是平衡的，树的高度是对数级别的。

4.2 计算树的高度 (Height)

树的高度指的是从根节点到最远叶子节点的最长路径上的边数。AVL树的高度是平衡的，计算时我们需要递归地计算左右子树的高度并返回较大的一个。

cpp 复制代码 
int Height() {
    return _Height(_root);  // 从根节点开始计算树的高度
}

int _Height(Node* root) {
    if (root == nullptr)
        return 0;  // 空树的高度为0

    int leftHeight = _Height(root->_left);  // 递归计算左子树的高度
    int rightHeight = _Height(root->_right);  // 递归计算右子树的高度

    return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;  // 返回较大值，并加1
}

该方法的时间复杂度为 O(N)，其中N为节点总数。虽然AVL树是平衡的，但在计算高度时需要遍历整个树。

4.3 计算节点数量 (Size)

节点数量是树中所有节点的总数。通过递归遍历树，计算左右子树的节点数量，并加上当前节点。

cpp 复制代码 
int Size() {
    return _Size(_root);  // 从根节点开始计算树的大小
}

int _Size(Node* root) {
    if (root == nullptr)
        return 0;  // 空树节点数量为0

    return _Size(root->_left) + _Size(root->_right) + 1;  // 左右子树的节点数量加1
}

该方法的时间复杂度为 O(N)，需要遍历整个树来计算节点总数。

4.4 树是否平衡 (IsBalanceTree)

为了验证AVL树的平衡性，我们需要检查每个节点的平衡因子，并确保它们的绝对值不超过1。如果树的任意节点的平衡因子大于1或小于-1，那么树就不平衡。

cpp 复制代码 
bool _IsBalanceTree(Node* root) {
    if (root == nullptr)
        return true;  // 空树是平衡的

    int leftHeight = _Height(root->_left);  // 左子树高度
    int rightHeight = _Height(root->_right);  // 右子树高度
    int diff = leftHeight - rightHeight;  // 计算平衡因子

    if (abs(diff) >= 2) {
        cout << root->_kv.first << "高度差异常" << endl;
        return false;  // 如果高度差大于等于2，树不平衡
    }

    if (root->_bf != diff) {
        cout << root->_kv.first << "平衡因子异常" << endl;
        return false;  // 如果平衡因子与实际高度差不符，树不平衡
    }

    // 递归检查左右子树是否平衡
    return _IsBalanceTree(root->_left) && _IsBalanceTree(root->_right);
}

该方法的时间复杂度为 O(N)，需要递归遍历整个树并计算每个节点的平衡因子。

五、性能分析与测试

5.1 性能分析

AVL树通过保持平衡，保证了插入、查找和删除操作的时间复杂度都为O(logN)，相比于普通的二叉查找树，AVL树避免了退化成链表的情况，极大提高了性能。

5.2 测试代码

下面是两个测试代码，用于验证AVL树的插入和查找操作。

cpp 复制代码 
// 测试代码
void TestAVLTree1()
{
	AVLTree<int, int> t;
	// 常规的测试用例
	//int a[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };
	// 特殊的带有双旋场景的测试用例
	int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };
	for (auto e : a)
	{
		t.Insert({ e, e });
		cout << "Insert:" << e << "->";
		cout << t.IsBalanceTree() << endl;
	}

	t.InOrder();
	cout << t.IsBalanceTree() << endl;
}


// 插入一堆随机值，测试平衡，顺便测试一下高度和性能等
void TestAVLTree2()
{
	const int N = 1000000;
	vector<int> v;
	v.reserve(N);
	srand((unsigned int)time(0));
	for (int i = 0; i < N; i++)
	{
		v.push_back(rand() + i);
	}

	size_t begin2 = clock();
	AVLTree<int, int> t;
	for (auto e : v)
	{
		t.Insert(make_pair(e, e));
	}
	size_t end2 = clock();

	cout << t.IsBalanceTree() << endl;

	cout << "Insert:" << end2 - begin2 << endl;
	cout << "Height:" << t.Height() << endl;
	cout << "Size:" << t.Size() << endl;

	size_t begin1 = clock();
	// 确定在的值
	/*for (auto e : v)
	{
		t.Find(e);
	}*/
	// 随机值
	for (int i = 0; i < N; i++)
	{
		t.Find((rand() + i));
	}

	size_t end1 = clock();
	cout << "Find:" << end1 - begin1 << endl;
}

六、全部代码

AVLTree.h

cpp 复制代码 
#pragma once


template<class K, class V>
struct AVLTreeNode
{
	pair<K, V> _kv;
	AVLTreeNode<K, V>* _left;
	AVLTreeNode<K, V>* _right;
	AVLTreeNode<K, V>* _parent;
	int _bf;

	AVLTreeNode(const pair<K, V>& kv)
		:_kv(kv)
		, _left(nullptr)
		, _right(nullptr)
		, _parent(nullptr)
		, _bf(0)
	{}
};


template<class K, class V>
class AVLTree
{
	typedef AVLTreeNode<K, V> Node;
public:
	bool Insert(const pair<K, V>& kv)
	{
		if (_root == nullptr)
		{
			_root = new Node(kv);
			return true;
		}

		Node* parent = nullptr;
		Node* cur = _root;
		while (cur)
		{
			if (cur->_kv.first < kv.first)
			{
				parent = cur;
				cur = cur->_right;
			}
			else if (cur->_kv.first > kv.first)
			{
				parent = cur;
				cur = cur->_left;
			}
			else
			{
				return false;
			}
		}

		cur = new Node(kv);
		if (parent->_kv.first < kv.first)
		{
			parent->_right = cur;
		}
		else
		{
			parent->_left = cur;
		}

		cur->_parent = parent;
		while (parent)
		{
			if (cur == parent->_left)
			{
				parent->_bf++;
			}
			else
			{
				parent->_bf--;
			}

			if (parent->_bf == 0)
			{
				break;
			}
			else if (parent->_bf == 1 || parent->_bf == -1)
			{
				cur = parent;
				parent = cur->_parent;
			}
			else if (parent->_bf == 2 || parent->_bf == -2)
			{
				//旋转
				if (parent->_bf == 2 && cur->_bf == 1)
				{
					RotateR(parent);
				}
				else if (parent->_bf == -2 && cur->_bf == -1)
				{
					RotateL(parent);
				}
				else if (parent->_bf == 2 && cur->_bf == -1)
				{
					RotateLR(parent);
				}
				else if (parent->_bf == -2 && cur->_bf == 1)
				{
					RotateRL(parent);
				}
				else
					assert(false);
				break;
			}
			else
			{
				assert(false);
			}
		}
		return true;
	}

	void InOrder()
	{
		_InOrder(_root);
	}

	bool IsBalanceTree()
	{
		return _IsBalanceTree(_root);
	}

	Node* Find(const K& key)
	{
		Node* cur = _root;
		while (cur)
		{
			if (cur->_kv.first < key)
				cur = cur->_right;
			else if (cur->_kv.first > key)
				cur = cur->_left;
			else
				return cur;
		}
		return nullptr;
	}

	int Height()
	{
		return _Height(_root);
	}

	int Size()
	{
		return _Size(_root);
	}


private:
	int _Size(Node* root)
	{
		if (root == nullptr)
			return 0;

		return _Size(root->_left) + _Size(root->_right) + 1;
	}

	int _Height(Node* root)
	{
		if (root == nullptr)
			return 0;

		int leftHeight = _Height(root->_left);
		int rightHeight = _Height(root->_right);

		return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
	}

	bool _IsBalanceTree(Node* root)
	{
		if (root == nullptr)
			return true;

		int leftHeight = _Height(root->_left);
		int rightHeight = _Height(root->_right);
		int diff = leftHeight - rightHeight;
		if (abs(diff) >= 2)
		{
			cout << root->_kv.first << "高度差异常" << endl;
			return false;
		}

		if (root->_bf != diff) {
			cout << root->_kv.first << "平衡因子异常" << endl;
			return false;
		}

		return _IsBalanceTree(root->_left) && _IsBalanceTree(root->_right);
	}

	void _InOrder(Node* root)
	{
		if (root == nullptr)
		{
			return;
		}

		_InOrder(root->_left);
		cout << root->_kv.first << ":" << root->_kv.second << " ";
		_InOrder(root->_right);
	}


	void RotateR(Node* parent)
	{
		Node* subL = parent->_left;
		Node* subLR = subL->_right;
		Node* ppNode = parent->_parent;
		parent->_left = subLR;
		if (subLR)
		{
			subLR->_parent = parent;
		}
		subL->_right = parent;
		parent->_parent = subL;
		if (parent == _root)
		{
			subL->_parent = nullptr;
			_root = subL;
		}
		else
		{
			subL->_parent = ppNode;
			if (parent == ppNode->_right)
				ppNode->_right = subL;
			else
				ppNode->_left = subL;
		}

		parent->_bf = 0;
		subL->_bf = 0;
	}

	void RotateL(Node* parent)
	{
		Node* subR = parent->_right;
		Node* ppNode = parent->_parent;
		Node* subRL = subR->_left;
		parent->_right = subRL;
		parent->_parent = subR;
		if (subRL)
		{
			subRL->_parent = parent;
		}
		subR->_left = parent;
		if (parent == _root)
		{
			_root = subR;
			subR->_parent = nullptr;
		}
		else
		{
			subR->_parent = ppNode;
			if (parent == ppNode->_right)
				ppNode->_right = subR;
			else
				ppNode->_left = subR;
		}

		parent->_bf = 0;
		subR->_bf = 0;

	}

	void RotateLR(Node* parent)
	{
		Node* subL = parent->_left;
		Node* subLR = subL->_right;
		int bf = subLR->_bf;
		RotateL(subL);
		RotateR(parent);
		if (bf == 1)
		{
			subLR->_bf = 0;
			subL->_bf = 0;
			parent->_bf = -1;
		}
		else if (bf == -1)
		{
			subLR->_bf = 0;
			subL->_bf = 1;
			parent->_bf = 0;
		}
		else if (bf == 0)
		{
			subL->_bf = subLR->_bf = parent->_bf = 0;
		}
		else
		{
			assert(false);
		}
	}

	void RotateRL(Node* parent)
	{
		Node* subR = parent->_right;
		Node* subRL = subR->_left;
		int bf = subRL->_bf;
		RotateR(subR);
		RotateL(parent);
		if (bf == 0)
		{
			parent->_bf = subR->_bf = subRL->_bf = 0;
		}
		else if (bf == 1)
		{
			subRL->_bf = 0;
			parent->_bf = 0;
			subR->_bf = -1;
		}
		else if (bf == -1)
		{
			subRL->_bf = 0;
			parent->_bf = 1;
			subR->_bf = 0;
		}
		else
		{
			assert(false);
		}
	}

	Node* _root = nullptr;
};

// 测试代码
void TestAVLTree1()
{
	AVLTree<int, int> t;
	// 常规的测试用例
	//int a[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };
	// 特殊的带有双旋场景的测试用例
	int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };
	for (auto e : a)
	{
		/*if (e == 14)
		{
			int x = 0;
		}*/

		t.Insert({ e, e });
		cout << "Insert:" << e << "->";
		cout << t.IsBalanceTree() << endl;
	}

	t.InOrder();
	cout << t.IsBalanceTree() << endl;
}





// 插入一堆随机值，测试平衡，顺便测试一下高度和性能等
void TestAVLTree2()
{
	const int N = 1000000;
	vector<int> v;
	v.reserve(N);
	srand((unsigned int)time(0));
	for (int i = 0; i < N; i++)
	{
		v.push_back(rand() + i);
	}

	size_t begin2 = clock();
	AVLTree<int, int> t;
	for (auto e : v)
	{
		t.Insert(make_pair(e, e));
	}
	size_t end2 = clock();

	cout << t.IsBalanceTree() << endl;

	cout << "Insert:" << end2 - begin2 << endl;
	cout << "Height:" << t.Height() << endl;
	cout << "Size:" << t.Size() << endl;

	size_t begin1 = clock();
	// 确定在的值
	/*for (auto e : v)
	{
		t.Find(e);
	}*/
	// 随机值
	for (int i = 0; i < N; i++)
	{
		t.Find((rand() + i));
	}

	size_t end1 = clock();
	cout << "Find:" << end1 - begin1 << endl;
}

Test.cpp

cpp 复制代码 
#define _CRT_SECURE_NO_WARNINGS 1

#include<iostream>
#include<assert.h>
#include<vector>
using namespace std;
#include"AVLTree.h"

int main()
{
	TestAVLTree1();
	TestAVLTree2();

	return 0;
}

七、总结与展望

随着数据量的不断增长，如何保持高效的查找与插入操作成为了现代计算机科学的核心问题之一。AVL树作为一种自平衡二叉查找树，凭借其稳定的时间复杂度和高效的性能，已广泛应用于各类需要动态数据结构支持的场景。未来，随着算法和硬件的进一步发展，AVL树的实现和优化将迎来更多挑战与机遇。我们期待看到更高效的树形结构和操作算法，不断推动计算机科学的前沿发展，同时也期待你在实现这些算法时能够继续探索与创新，为我们带来更多启发和思考。

以上就是关于【C++篇】树影摇曳，旋转无声：探寻AVL树的平衡之道的内容啦，各位大佬有什么问题欢迎在评论区指正，或者私信我也是可以的啦，您的支持是我创作的最大动力！❤️

相关推荐
RAN_PAND8 分钟前
STL介绍1：vector、pair、string、queue、map
开发语言·c++·算法
左灯右行的爱情2 小时前
Redis数据结构总结-listPack
数据结构·数据库·redis
fai厅的秃头姐！2 小时前
C语言03
c语言·数据结构·算法
醉城夜风~3 小时前
[数据结构]单链表详解
数据结构·链表
lisanndesu3 小时前
动态规划
算法·动态规划
myprogramc3 小时前
十大排序算法
数据结构·算法·排序算法
记得早睡~3 小时前
leetcode150-逆波兰表达式求值
javascript·算法·leetcode
修己xj3 小时前
算法系列之贪心算法
算法
qy发大财3 小时前
跳跃游戏(力扣55)
算法·leetcode
热门推荐
01太炸裂了！清华大学deepseek从入门到精通使用手册又出第三版了，《普通人如何抓住DeepSeek红利》（无套路，直接下载）02如何在WPS和Word/Excel中直接使用DeepSeek功能03DeepSeek本地部署详细指南04DeepSeek各版本说明与优缺点分析05本地部署DeepSeek教程（Mac版本）06DeepSeek r1本地安装全指南07本地化部署AI知识库：基于Ollama+DeepSeek+AnythingLLM保姆级教程08DeepSeek R1本地化部署 Ollama + Chatbox 打造最强 AI 工具09在Windows下安装Ollama并体验DeepSeek r1大模型10本地部署DeepSeek后的调用与删除全攻略