状态反馈控制系统 -全维状态观测器的实现
状态观测器的建立解决了受控系统不能测量的状态重构问题,使得状态反馈的工程实现成为可能。
考虑到系统的状态方程表达式,如果{A,B}可控,{A,C}可观,且安装系统的性能指标,可以确定状况反馈控制律u=-Kx+v。为了实现状态反馈,还需要引入状态观测器以重构系统的状态。引入状态观测器之后的系统方框图如下所示:
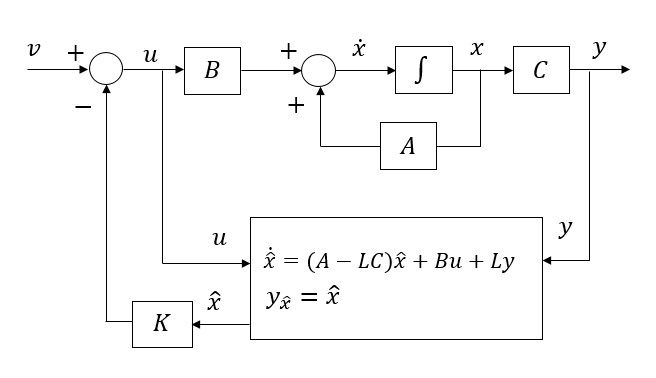
所以观测器的状态方程为:
上述状态方程中L为未知数,如果能够确定L的参数,我们就可以得到状态的观测值。
根据系统方程:
观测器方程:
结合上述两个方程可知:
如果观测器的极点在复平面的左半平面,那么e渐进稳定。这样估算的状态变量就会无限逼近真实的状态变量。通常来讲,观测器的极点要比状态控制器的极点大2~6倍,这样观测器会更快的收敛。
例如
试用全维状态观测器和极点配置设计闭环系统。
MATLAB代码如下:
clear all;clc;
A=[0 1;0 0];
B=[0;1];
C=[1 0];
D=0;
C0=[1 0 ;0 1];
D0=[0 ; 0];
Po=[-10 -20];
Px=[-2 -5];
K=place(A,B,Px);
L=(place(A',C',Po))';
Ao=A-L*C;
Bo=[B L];
Co=[1 0 ;0 1];
Do=[0 0; 0 0];Simulink如下所示,文件下载这里
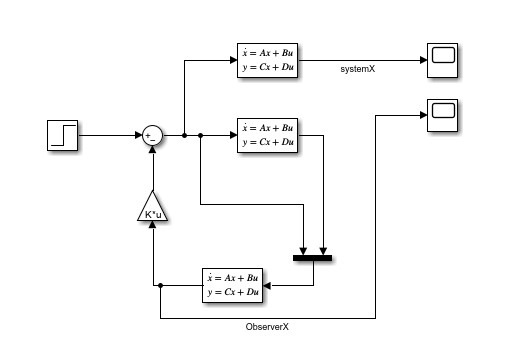
程序运行结果如下:
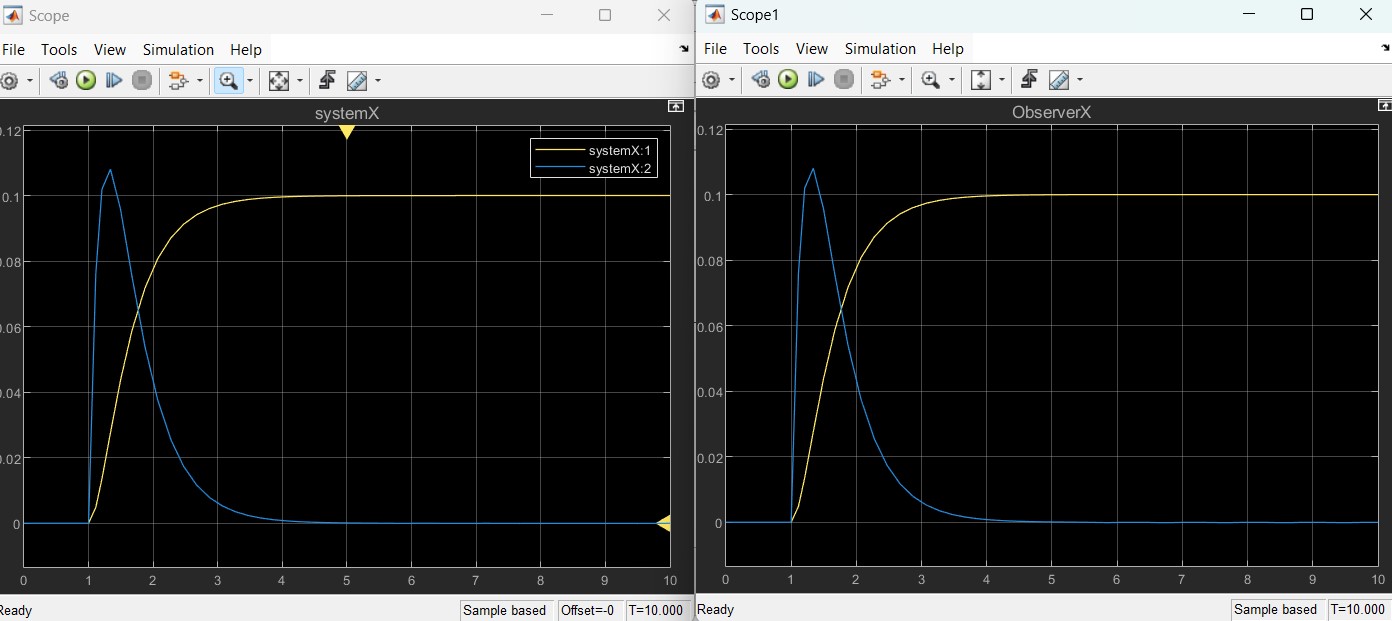
由上图可知:左边系统状态量和右手边估算的系统系统状态量一样。
所以状态观测器的建立解决了受控系统不能测量的状态重构问题,使得状态反馈的工程实现成为可能。
最后,欢迎大家有问题给我留言。
非常感谢小伙伴们的-点赞-收藏-加关注。