KD树 - 技术栈

KD Tree

What is KD tree

KD树是K-dimension tree的缩写，是对数据点在k维空间（如二维(x，y)，三维(x，y，z)，k维(x，y，z..)）中划分的一种数据结构，主要应用于多维空间关键数据的搜索（如：范围搜索和最近邻搜索）。本质上说，KD-树就是一种平衡二叉树。
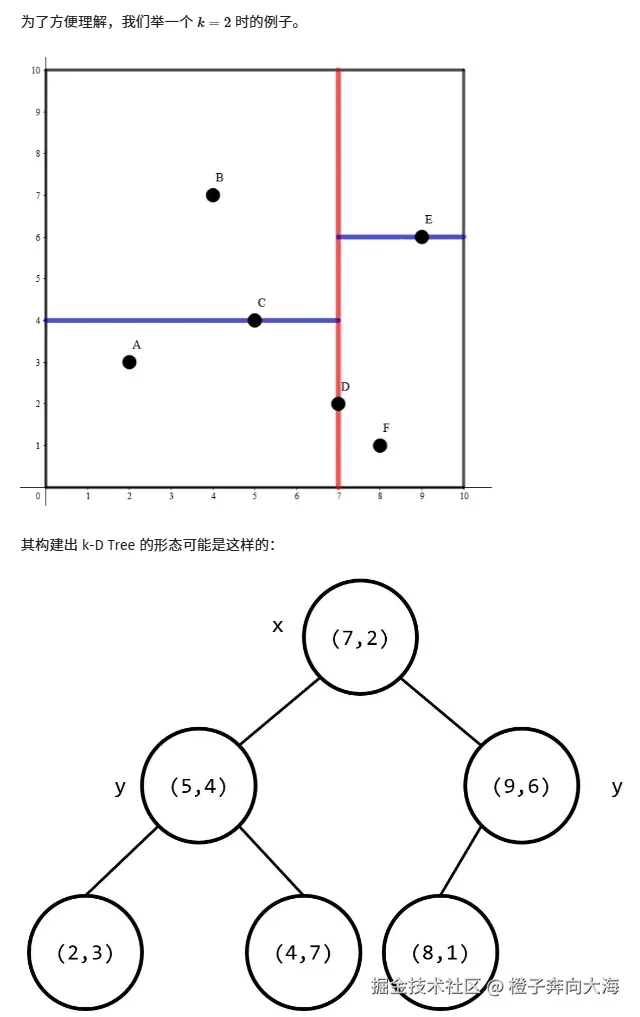
举个例子，大家可以看下面这张图片。

对于平面点集的划分分为两种，按照x划分 （也就是图中竖线，将点尽量分为左右各一半）和按照y划分（也就是图中横线，将点尽量分为上下各一半）。

再来一个更容易理解的例子，来自OI Wiki

How to build KD tree

KD tree结构体组成

Splitting axis
Splitting value
Data
Left pointer
Right pointer

构建策略

Divide based on order of point insertion
- 事先不知道点的整体分布，而是来一个点插入一个点
Divide by finding median
- 实现知道点的整体分布情况
Divide perpendicular to the axis with widest spread
- 分割的轴可能不交替
......

基于点插入的顺序进行划分

整体的构建思路其实就和在平面划分点集是一样的，先比较x坐标，再比较y坐标。

arduino 复制代码

Node *insertRec(Node *root, int point[], unsigned depth)
{
    if (root == NULL)
       return newNode(point);
    // 确定比较的维度
    unsigned cd = depth % k;
    // 与root的 cd 维数据进行对比
    if (point[cd] < (root->point[cd]))
        root->left =insertRec(root->left, point, depth + 1);
    else
        root->right =insertRec(root->right, point, depth + 1);
    return root;
}

Node* insert(Node *root, int point[])
{
    return insertRec(root, point, 0);
}

例如，加入点的插入顺序为 (3, 6), (17, 15), (13, 15), (6, 12), (9, 1), (2, 7), (10, 19)，那么构建的KD树应当展现为

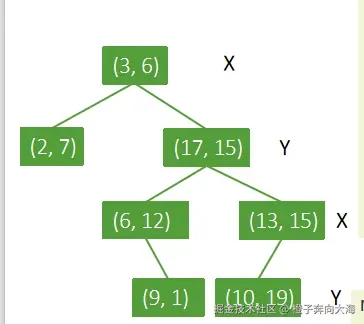
像二叉搜索树 (BST) 一样，我们期望插入操作的时间复杂度为O(log \ n)，因为操作需要沿从根节点到叶节点的路径进行，而在平衡树中其深度为log \ n（其中 n 为节点数，等同于点的数量）。
然而，存在一个明确的退化情况：如果后续插入的点在每个维度上的坐标都持续增大，那么树结构就会退化成一条链（线形结构），其高度为 O(n)。考虑到节点深度累加1+2+···+n = O(n²)，在最坏情况下，构建一棵 KD 树可能需要二次方时间。
然而很多情况下，我们都是已经知道点集的全体情况的，这时候我们就可以对算法进行优化来降低复杂度。

基于中位数的构建

关键在于将点集精确地均分到两个子树中，是理论上最优的分割策略。这意味着分割操作应当基于中位数（值）来进行。
下面给出一个构建示例。

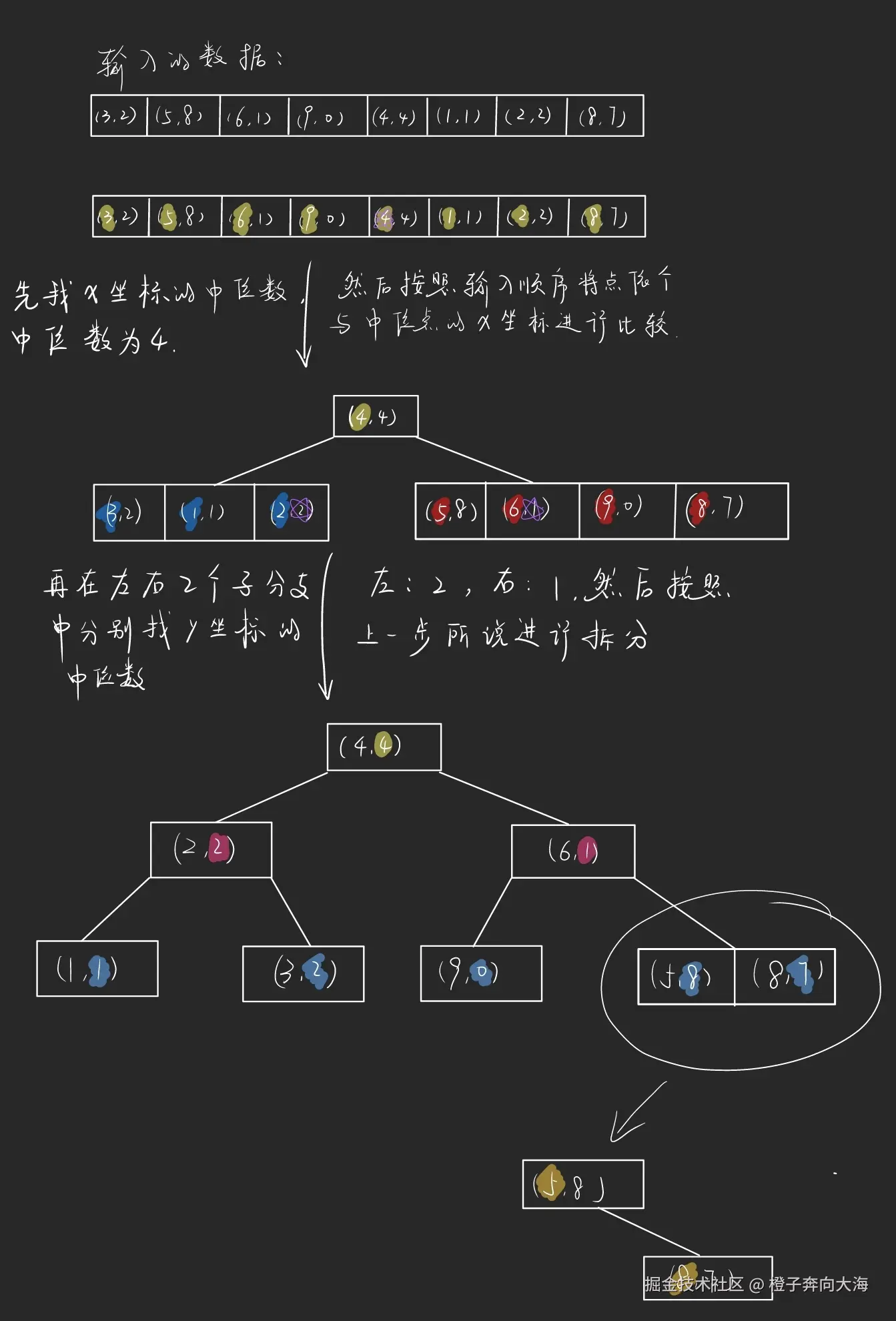
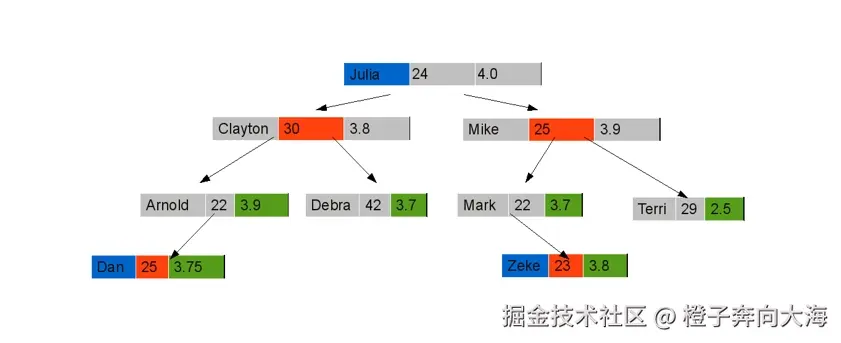
有人就问了，为啥这么麻烦啊，只通过x坐标排序不好吗？为啥还要弄个交替的？那么假如我们面临的数据是下面这样的，我们该如何建树呢？
1. 依照姓名排序，找到中位值。
2. 依据年龄排序，找到两棵子树的中位数。
3. 最后就是依据绩点排序，我们来看一下整体步骤。

KD tree的Insert , delete和search

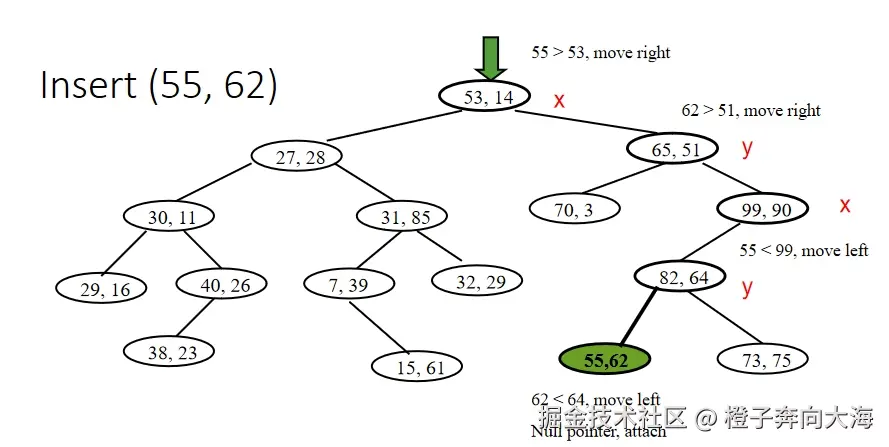
Insert

插入策略其实和构建策略一样，还是每个维度的数据依次比较，决定往左子树走还是往右子树走。

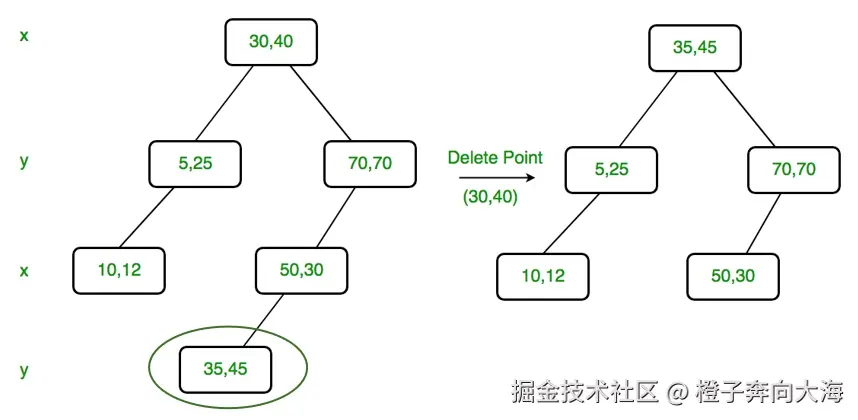
Delete

<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> 分割维度 c d = 结点深度 d e p t h % 空间维度数 k 分割维度cd=结点深度depth\ \%\ 空间维度数k </math>分割维度cd=结点深度depth % 空间维度数k

其实就是在决定到这一层的数据是依据x的顺序还是y的顺序还是别的维度的数据顺序。

如果当前节点不是要删除的节点
- 那么搜索找到要删除的点。
如果是当前结点是待删除结点root且有右子树
- 在 root 的 右子树 中沿着当前维度 cd 查找 最小值 节点 min。注意：这里是找右子树中 cd 维度上的最小值，这类似于二叉搜索树（BST）中用右子树的最小值（中序后继）来替换被删除节点。
如果是当前结点是待删除结点root，没有右子树但是有左子树
- 在 root 的 左子树 中，沿着当前维度 cd 查找 最小值 节点 min。
- 注意：这里的逻辑与标准 BST 删除稍有不同，标准 BST 在只有左子树时通常用左子树的最大值（中序前驱）替换。这里选择在左子树中仍然查找最小值。
如果是当前结点是待删除结点root而且是叶子结点
- 直接释放该叶子节点的内存。

arduino 复制代码

Node *deleteNodeRec(Node *root, int point[], int depth)
{
    // Given point is not present
    if (root == NULL)
        return NULL;
    // Find dimension of current node
    int cd = depth % k;
    // If the point to be deleted is present at root
    if (arePointsSame(root->point, point))
    {
        // 2.b) If right child is not NULL
        if (root->right != NULL) 
        {
            // Find minimum of root's dimension in right subtree
            Node *min = findMin(root->right, cd);
            // Copy the minimum to root
            copyPoint(root->point, min->point);
            // Recursively delete the minimum
            root->left = deleteNodeRec(root->right, min->point, depth+1);
        }
        else if (root->left != NULL) // same as above
        {
            Node *min = findMin(root->left, cd);
            copyPoint(root->point, min->point);
            root->right = deleteNodeRec(root->left, min->point, depth+1);
        }
        else // If node to be deleted is leaf node
        {
            delete root;
            return NULL;
        }
        return root;
    }

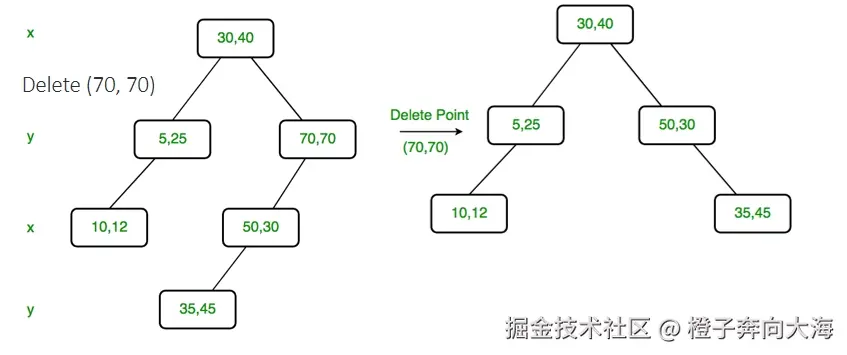
我们来看两个例子。