《算法导论》第 4 章 - 分治策略

引言

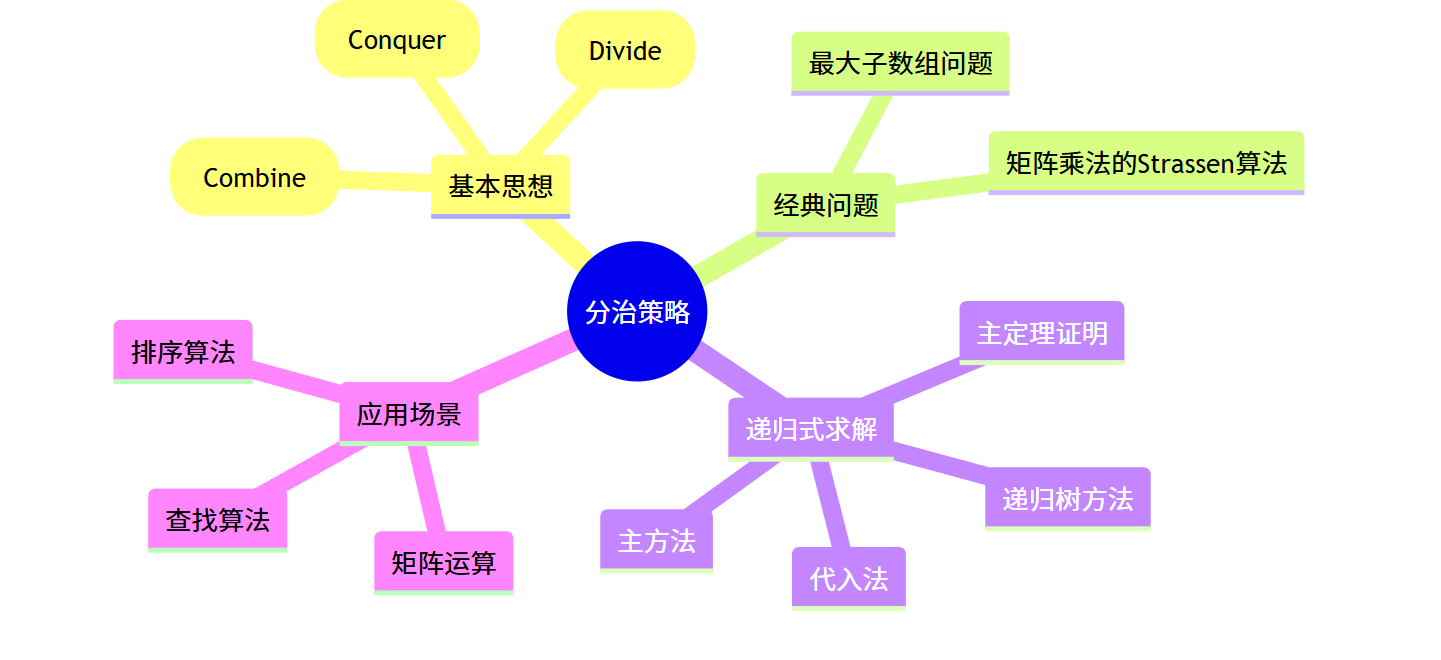
分治策略（Divide and Conquer）是算法设计中的一种重要思想，其核心思想是将一个复杂问题分解为若干个规模较小的子问题，递归地解决这些子问题，然后将子问题的解合并，从而得到原问题的解。分治策略在许多高效算法中都有应用，如快速排序、归并排序、Strassen 矩阵乘法等。

本章将详细讲解《算法导论》第 4 章关于分治策略的内容，包括经典问题、算法设计、递归式求解方法等，并通过完整的 C++ 代码实现帮助读者深入理解和实践。

思维导图

4.1 最大子数组问题

问题定义

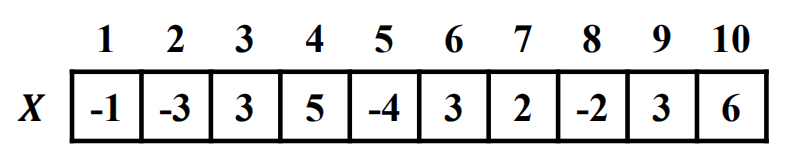
最大子数组问题（Maximum Subarray Problem）是指：给定一个整数数组，找到一个具有最大和的连续子数组（至少包含一个元素），返回其最大和。

例如，对于数组 [-2, 1, -3, 4, -1, 2, 1, -5, 4]，其最大子数组是 [4, -1, 2, 1]，最大和为 6。

分治思路

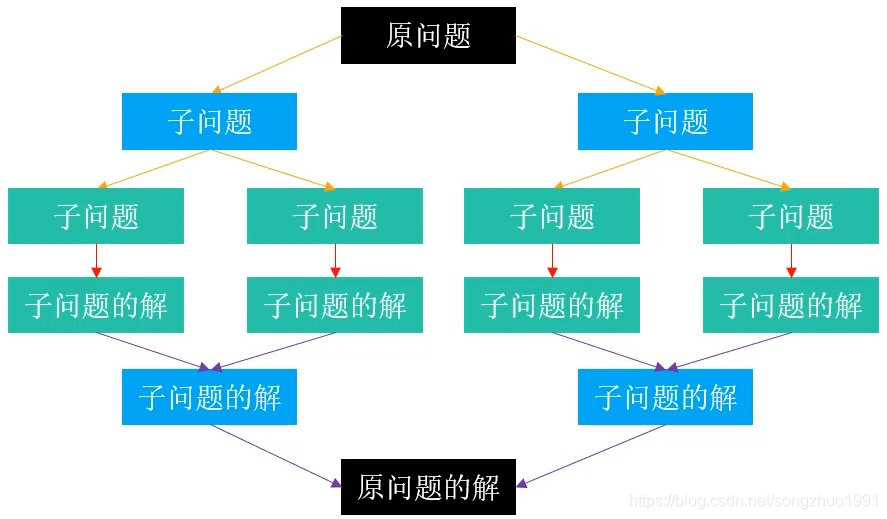
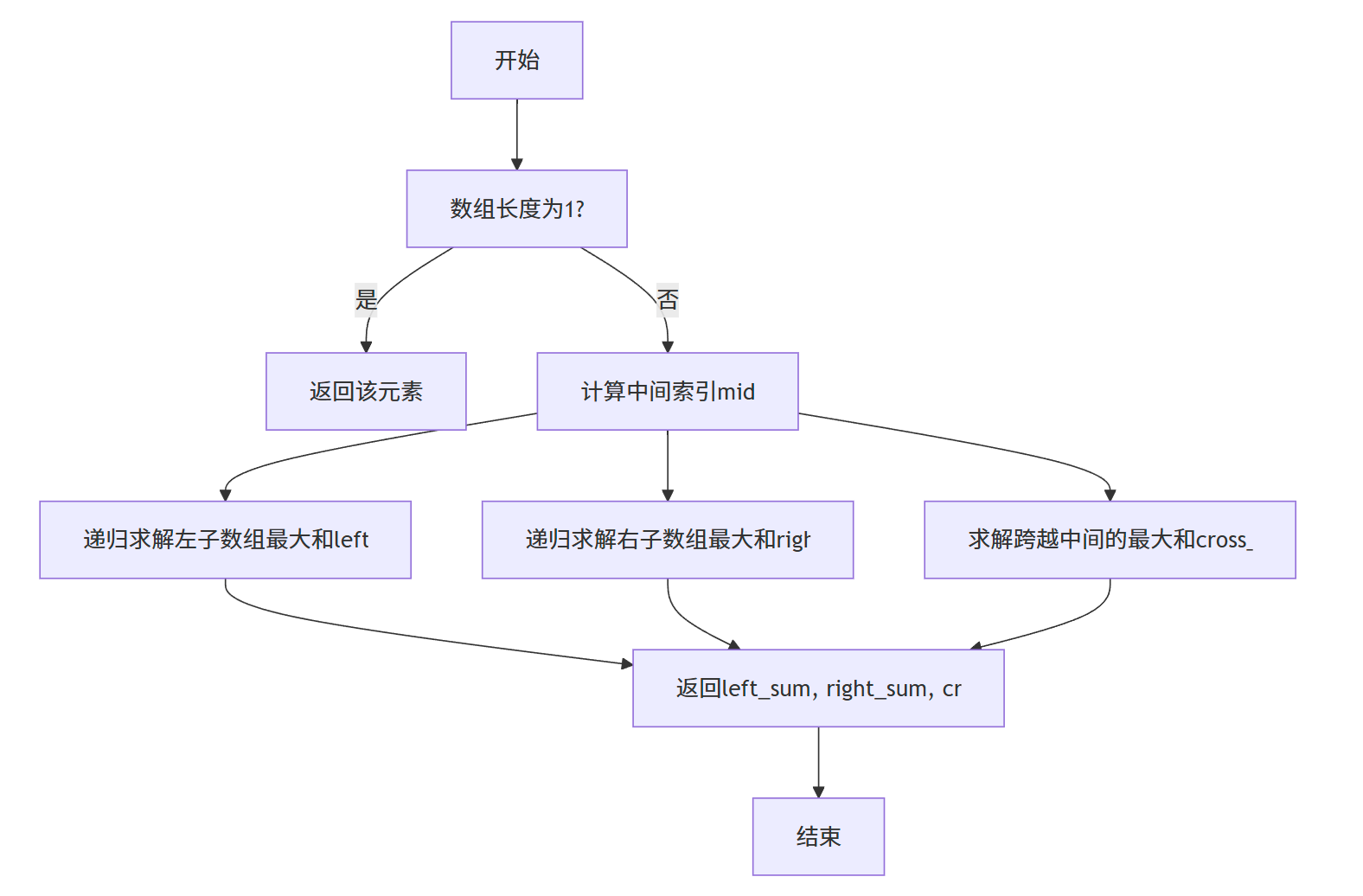
使用分治策略解决最大子数组问题的步骤如下：

分解：将数组从中间分成左右两个子数组。
解决：递归地求解左右两个子数组的最大子数组。
合并：求出跨越中间点的最大子数组，然后与左右子数组的最大子数组比较，取最大者作为原数组的最大子数组。

其中，跨越中间点的最大子数组 求解是关键，需要分别从中间点向左、向右寻找最大子数组，然后合并这两个子数组。

流程图

代码实现

复制代码

#include <iostream>
#include <vector>
#include <climits> // 用于INT_MIN
#include <algorithm> // 用于max函数

using namespace std;

/**
 * 计算跨越中间点的最大子数组和
 * @param nums 输入数组
 * @param left 左边界索引
 * @param mid 中间索引
 * @param right 右边界索引
 * @return 跨越中间点的最大子数组和
 */
int maxCrossingSubarray(const vector<int>& nums, int left, int mid, int right) {
    // 计算左半部分（从mid向左）的最大和
    int left_sum = INT_MIN;
    int sum = 0;
    for (int i = mid; i >= left; --i) {
        sum += nums[i];
        if (sum > left_sum) {
            left_sum = sum;
        }
    }

    // 计算右半部分（从mid+1向右）的最大和
    int right_sum = INT_MIN;
    sum = 0;
    for (int i = mid + 1; i <= right; ++i) {
        sum += nums[i];
        if (sum > right_sum) {
            right_sum = sum;
        }
    }

    // 返回左右两部分的和（跨越中间点）
    return left_sum + right_sum;
}

/**
 * 递归求解最大子数组和
 * @param nums 输入数组
 * @param left 左边界索引
 * @param right 右边界索引
 * @return 最大子数组和
 */
int maxSubarrayRecursive(const vector<int>& nums, int left, int right) {
    // 基本情况：数组只有一个元素
    if (left == right) {
        return nums[left];
    }

    // 计算中间索引
    int mid = (left + right) / 2;

    // 递归求解左子数组、右子数组的最大和
    int left_sum = maxSubarrayRecursive(nums, left, mid);
    int right_sum = maxSubarrayRecursive(nums, mid + 1, right);

    // 求解跨越中间的最大和
    int cross_sum = maxCrossingSubarray(nums, left, mid, right);

    // 返回三者中的最大值
    return max({left_sum, right_sum, cross_sum});
}

/**
 * 最大子数组问题的分治解法
 * @param nums 输入数组
 * @return 最大子数组和
 */
int maxSubArray(const vector<int>& nums) {
    if (nums.empty()) {
        throw invalid_argument("数组不能为空");
    }
    return maxSubarrayRecursive(nums, 0, nums.size() - 1);
}

// 测试函数
int main() {
    vector<int> nums = {-2, 1, -3, 4, -1, 2, 1, -5, 4};
    cout << "数组: ";
    for (int num : nums) {
        cout << num << " ";
    }
    cout << endl;

    try {
        int result = maxSubArray(nums);
        cout << "最大子数组和: " << result << endl; // 预期输出：6
    } catch (const invalid_argument& e) {
        cout << "错误: " << e.what() << endl;
    }

    return 0;
}

代码说明

maxCrossingSubarray 函数：计算跨越中间点的最大子数组和，分别从中间点向左、向右累加，记录最大和。
maxSubarrayRecursive 函数：递归实现分治策略，分解问题并合并结果。
maxSubArray 函数：包装函数，处理边界情况并调用递归函数。
时间复杂度：O (n log n)，其中 n 是数组长度。递归树的深度为 O (log n)，每层的合并操作（计算跨越中间的最大子数组）为 O (n)。

4.2 矩阵乘法的 Strassen 算法

问题背景

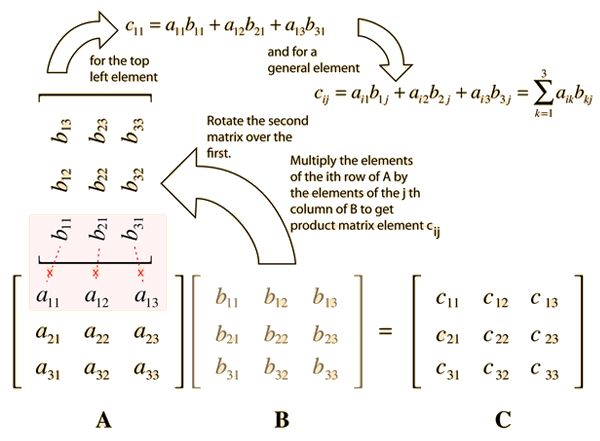
矩阵乘法是线性代数中的基本运算。对于两个 n×n 的矩阵 A 和 B，它们的乘积 C 也是一个 n×n 的矩阵，其中 C [i][j] = Σ(A [i][k] * B [k][j]) （k 从 1 到 n）。

普通矩阵乘法的时间复杂度为 O (n³)，而 Strassen 算法通过分治策略将时间复杂度降低到了 O (n^log₂7) ≈ O (n²・⁸⁰⁷)。

Strassen 算法步骤

分解：将矩阵 A、B、C 各分解为 4 个 n/2×n/2 的子矩阵：

plaintext
复制代码
```
A = [[A₁₁, A₁₂],    B = [[B₁₁, B₁₂],    C = [[C₁₁, C₁₂],
     [A₂₁, A₂₂]]         [B₂₁, B₂₂]]         [C₂₁, C₂₂]]
```
其中，C₁₁ = A₁₁B₁₁ + A₁₂B₂₁

C₁₂ = A₁₁B₁₂ + A₁₂B₂₂

C₂₁ = A₂₁B₁₁ + A₂₂B₂₁

C₂₂ = A₂₁B₁₂ + A₂₂B₂₂
计算 7 个中间矩阵：
- M₁ = (A₁₁ + A₂₂) * (B₁₁ + B₂₂)
- M₂ = (A₂₁ + A₂₂) * B₁₁
- M₃ = A₁₁ * (B₁₂ - B₂₂)
- M₄ = A₂₂ * (B₂₁ - B₁₁)
- M₅ = (A₁₁ + A₁₂) * B₂₂
- M₆ = (A₂₁ - A₁₁) * (B₁₁ + B₁₂)
- M₇ = (A₁₂ - A₂₂) * (B₂₁ + B₂₂)
计算 C 的子矩阵：
- C₁₁ = M₁ + M₄ - M₅ + M₇
- C₁₂ = M₃ + M₅
- C₂₁ = M₂ + M₄
- C₂₂ = M₁ - M₂ + M₃ + M₆
组合：将 C₁₁、C₁₂、C₂₁、C₂₂组合成矩阵 C。

代码实现

复制代码

#include <iostream>
#include <vector>
#include <cmath> // 用于ceil函数

using namespace std;

// 定义矩阵类型
using Matrix = vector<vector<int>>;

/**
 * 矩阵加法
 * @param A 矩阵A
 * @param B 矩阵B
 * @return 矩阵A + B
 */
Matrix add(const Matrix& A, const Matrix& B) {
    int n = A.size();
    Matrix result(n, vector<int>(n));
    for (int i = 0; i < n; ++i) {
        for (int j = 0; j < n; ++j) {
            result[i][j] = A[i][j] + B[i][j];
        }
    }
    return result;
}

/**
 * 矩阵减法
 * @param A 矩阵A
 * @param B 矩阵B
 * @return 矩阵A - B
 */
Matrix subtract(const Matrix& A, const Matrix& B) {
    int n = A.size();
    Matrix result(n, vector<int>(n));
    for (int i = 0; i < n; ++i) {
        for (int j = 0; j < n; ++j) {
            result[i][j] = A[i][j] - B[i][j];
        }
    }
    return result;
}

/**
 * 普通矩阵乘法（用于小矩阵或边界情况）
 * @param A 矩阵A
 * @param B 矩阵B
 * @return 矩阵A * B
 */
Matrix multiplyNaive(const Matrix& A, const Matrix& B) {
    int n = A.size();
    Matrix result(n, vector<int>(n, 0));
    for (int i = 0; i < n; ++i) {
        for (int k = 0; k < n; ++k) {
            if (A[i][k] != 0) { // 优化：跳过零元素
                for (int j = 0; j < n; ++j) {
                    result[i][j] += A[i][k] * B[k][j];
                }
            }
        }
    }
    return result;
}

/**
 * 将大矩阵分割为4个子矩阵
 * @param parent 父矩阵
 * @param child 子矩阵（输出）
 * @param row 子矩阵在父矩阵中的起始行（0或n/2）
 * @param col 子矩阵在父矩阵中的起始列（0或n/2）
 * @param n 子矩阵的大小
 */
void splitMatrix(const Matrix& parent, Matrix& child, int row, int col, int n) {
    for (int i = 0; i < n; ++i) {
        for (int j = 0; j < n; ++j) {
            child[i][j] = parent[row + i][col + j];
        }
    }
}

/**
 * 将4个子矩阵合并为大矩阵
 * @param parent 父矩阵（输出）
 * @param child 子矩阵
 * @param row 子矩阵在父矩阵中的起始行（0或n/2）
 * @param col 子矩阵在父矩阵中的起始列（0或n/2）
 * @param n 子矩阵的大小
 */
void mergeMatrix(Matrix& parent, const Matrix& child, int row, int col, int n) {
    for (int i = 0; i < n; ++i) {
        for (int j = 0; j < n; ++j) {
            parent[row + i][col + j] = child[i][j];
        }
    }
}

/**
 * Strassen算法实现矩阵乘法
 * @param A 矩阵A
 * @param B 矩阵B
 * @return 矩阵A * B
 */
Matrix strassenMultiply(const Matrix& A, const Matrix& B) {
    int n = A.size();

    // 基本情况：当矩阵大小较小时，使用普通乘法（效率更高）
    if (n <= 64) { // 阈值可调整，通常取64或32
        return multiplyNaive(A, B);
    }

    // 计算新的矩阵大小（确保是2的幂，便于分割）
    int new_size = 1;
    while (new_size < n) {
        new_size <<= 1; // 等价于new_size *= 2
    }

    // 补全矩阵为new_size x new_size（不足部分补0）
    Matrix A_padded(new_size, vector<int>(new_size, 0));
    Matrix B_padded(new_size, vector<int>(new_size, 0));
    for (int i = 0; i < n; ++i) {
        for (int j = 0; j < n; ++j) {
            A_padded[i][j] = A[i][j];
            B_padded[i][j] = B[i][j];
        }
    }

    // 分割矩阵为4个子矩阵
    int half = new_size / 2;
    Matrix A11(half, vector<int>(half));
    Matrix A12(half, vector<int>(half));
    Matrix A21(half, vector<int>(half));
    Matrix A22(half, vector<int>(half));
    Matrix B11(half, vector<int>(half));
    Matrix B12(half, vector<int>(half));
    Matrix B21(half, vector<int>(half));
    Matrix B22(half, vector<int>(half));

    splitMatrix(A_padded, A11, 0, 0, half);
    splitMatrix(A_padded, A12, 0, half, half);
    splitMatrix(A_padded, A21, half, 0, half);
    splitMatrix(A_padded, A22, half, half, half);

    splitMatrix(B_padded, B11, 0, 0, half);
    splitMatrix(B_padded, B12, 0, half, half);
    splitMatrix(B_padded, B21, half, 0, half);
    splitMatrix(B_padded, B22, half, half, half);

    // 计算7个中间矩阵
    Matrix M1 = strassenMultiply(add(A11, A22), add(B11, B22));
    Matrix M2 = strassenMultiply(add(A21, A22), B11);
    Matrix M3 = strassenMultiply(A11, subtract(B12, B22));
    Matrix M4 = strassenMultiply(A22, subtract(B21, B11));
    Matrix M5 = strassenMultiply(add(A11, A12), B22);
    Matrix M6 = strassenMultiply(subtract(A21, A11), add(B11, B12));
    Matrix M7 = strassenMultiply(subtract(A12, A22), add(B21, B22));

    // 计算C的4个子矩阵
    Matrix C11 = add(subtract(add(M1, M4), M5), M7);
    Matrix C12 = add(M3, M5);
    Matrix C21 = add(M2, M4);
    Matrix C22 = add(subtract(add(M1, M3), M2), M6);

    // 合并子矩阵
    Matrix C_padded(new_size, vector<int>(new_size));
    mergeMatrix(C_padded, C11, 0, 0, half);
    mergeMatrix(C_padded, C12, 0, half, half);
    mergeMatrix(C_padded, C21, half, 0, half);
    mergeMatrix(C_padded, C22, half, half, half);

    // 截取结果为n x n矩阵（去除补全的部分）
    Matrix C(n, vector<int>(n));
    for (int i = 0; i < n; ++i) {
        for (int j = 0; j < n; ++j) {
            C[i][j] = C_padded[i][j];
        }
    }

    return C;
}

/**
 * 打印矩阵
 * @param mat 要打印的矩阵
 */
void printMatrix(const Matrix& mat) {
    for (const auto& row : mat) {
        for (int val : row) {
            cout << val << "\t";
        }
        cout << endl;
    }
}

// 测试函数
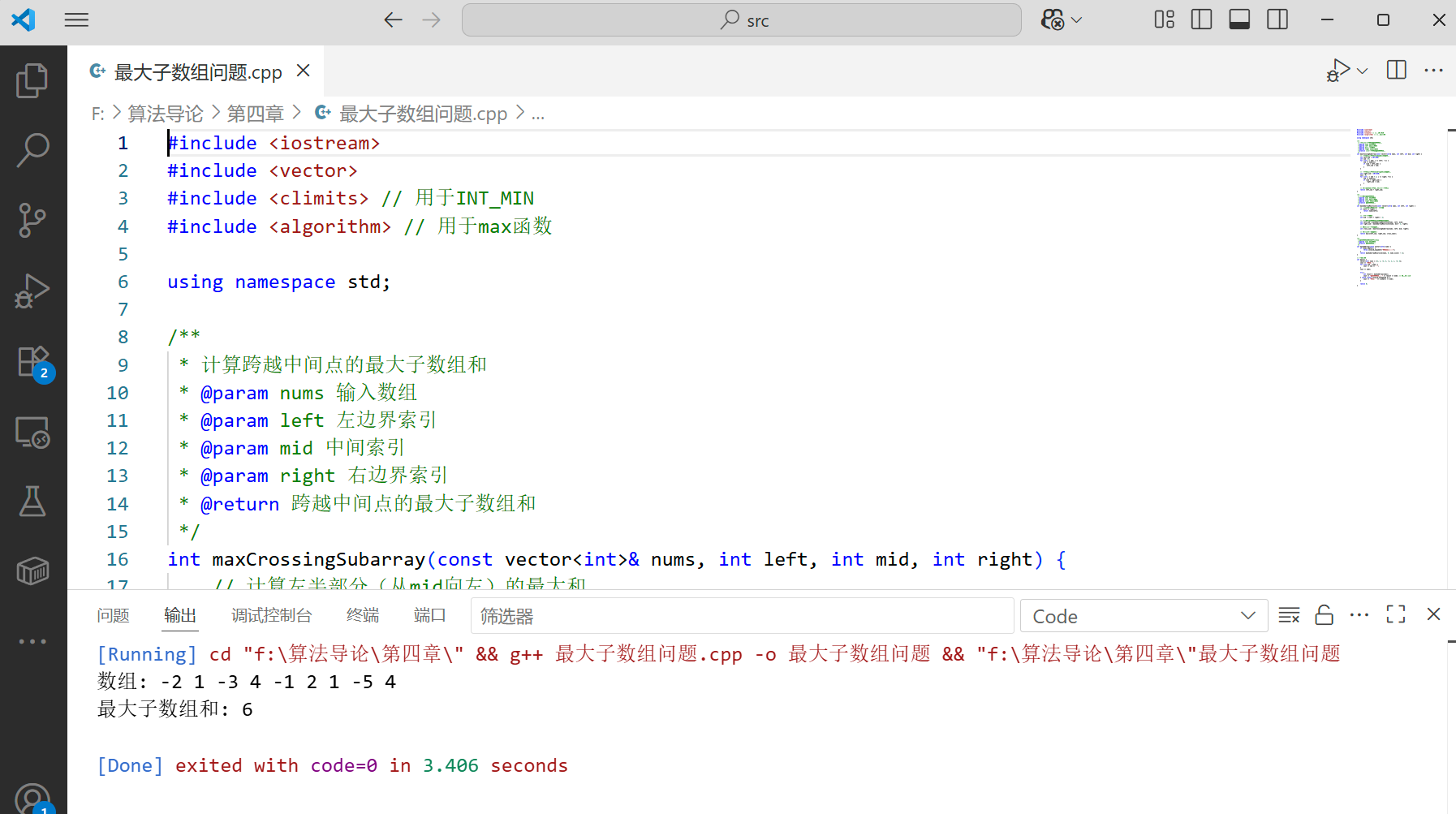
int main() {
    // 测试用例：2x2矩阵乘法
    Matrix A = {{1, 2},
                {3, 4}};
    Matrix B = {{5, 6},
                {7, 8}};

    cout << "矩阵A:" << endl;
    printMatrix(A);
    cout << endl << "矩阵B:" << endl;
    printMatrix(B);

    Matrix C_naive = multiplyNaive(A, B);
    cout << endl << "普通乘法结果:" << endl;
    printMatrix(C_naive);

    Matrix C_strassen = strassenMultiply(A, B);
    cout << endl << "Strassen算法结果:" << endl;
    printMatrix(C_strassen);

    // 测试用例：3x3矩阵乘法
    Matrix D = {{1, 2, 3},
                {4, 5, 6},
                {7, 8, 9}};
    Matrix E = {{9, 8, 7},
                {6, 5, 4},
                {3, 2, 1}};

    cout << endl << "矩阵D:" << endl;
    printMatrix(D);
    cout << endl << "矩阵E:" << endl;
    printMatrix(E);

    Matrix F_naive = multiplyNaive(D, E);
    cout << endl << "普通乘法结果:" << endl;
    printMatrix(F_naive);

    Matrix F_strassen = strassenMultiply(D, E);
    cout << endl << "Strassen算法结果:" << endl;
    printMatrix(F_strassen);

    return 0;
}

代码说明

代码中实现了矩阵的加法、减法、普通乘法和 Strassen 乘法。
为了处理非 2 的幂大小的矩阵，代码中进行了补全操作（不足部分补 0）。
当矩阵大小较小时（如≤64），使用普通乘法效率更高，因此设置了阈值。
Strassen 算法通过减少递归乘法的次数（7 次 vs 普通分治的 8 次）来降低时间复杂度。

4.3 用代入法求解递归式

方法概述

代入法（Substitution Method）是求解递归式的一种基本方法，其步骤如下：

猜测解的形式：根据递归式的结构，猜测解的渐近形式（如 T (n) = O (n log n)）。
验证猜测：用数学归纳法证明猜测的解是正确的，即证明存在常数 c > 0 和 n₀，使得对于所有 n ≥ n₀，都有 T (n) ≤ c・g (n)（其中 g (n) 是猜测的解）。

示例解析

示例 1：求解递归式 T (n) = 2T (n/2) + n，其中 T (1) = 1。

猜测解：观察递归式，其形式与归并排序的递归式相同，猜测 T (n) = O (n log n)。
验证：
- 假设对于所有 k <n，有 T (k) ≤ c・k log k（归纳假设）。
- 对于 n，有：
  T (n) = 2T (n/2) + n
  ≤ 2·c·(n/2) log(n/2) + n
  = c·n (log n - log 2) + n
  = c·n log n - c·n + n
  ≤ c・n log n （当 c ≥ 1 时，-c・n + n ≤ 0）
- 因此，T (n) = O (n log n) 得证。

示例 2：求解递归式 T (n) = T (n/2) + T (n/4) + n，其中 T (1) = 1。

猜测解：猜测 T (n) = O (n)。
验证：
- 假设对于所有 k <n，有 T (k) ≤ c・k（归纳假设）。
- 对于 n，有：
  T (n) = T (n/2) + T (n/4) + n
  ≤ c·(n/2) + c·(n/4) + n
  = (3c/4)·n + n
  = n·(3c/4 + 1)
  ≤ c・n （当 c ≥ 4 时，3c/4 + 1 ≤ c）
- 因此，T (n) = O (n) 得证。

关键技巧

猜测解时，可以参考类似的递归式（如主方法中的典型形式）。
若初始猜测不成立，可以调整猜测的形式（如增加低阶项）。
注意归纳基础的验证（如 n=1,2 等小值时是否满足条件）。

4.4 用递归树方法求解递归式

方法概述

递归树（Recursion Tree）是一种可视化递归式的方法，通过将递归式展开为一棵树，每一层代表递归的一个层次，节点的值代表该层子问题的代价。求解步骤如下：

构建递归树：将递归式分解为树的形式，根节点是原问题的代价，子节点是子问题的代价。
计算每一层的代价：递归树的每一层对应递归的一个深度，计算该层所有节点的代价之和。
求和：将所有层的代价相加，得到递归式的解的渐近上界（或下界）。

示例解析

示例 1：求解递归式 T (n) = 3T (n/4) + n²。

构建递归树：
- 根节点：代价为 n²，有 3 个子节点（对应 3T (n/4)）。
- 第 1 层：每个子节点的代价为 (n/4)²，共 3 个节点，总代价为 3・(n/4)²。
- 第 2 层：每个子节点的代价为 (n/16)²，共 3² 个节点，总代价为 3²・(n/16)²。
- ...
- 第 k 层：总代价为 3ᵏ・(n/4ᵏ)² = n²・(3/16)ᵏ。
确定树的深度：当 n/4ᵏ = 1 时，k = log₄n，因此树的深度为 log₄n。
求和：

T(n) = n² + 3·(n/4)² + 3²·(n/16)² + ... + 3ᵏ·(n/4ᵏ)²

= n²·[1 + (3/16) + (3/16)² + ... + (3/16)^log₄n]

这是一个等比数列，公比 r = 3/16 <1，无穷级数和为 1/(1 - r) = 16/13。

因此，T (n) = O (n²)。

示例 2：求解递归式 T (n) = T (n/3) + T (2n/3) + n。

构建递归树：
- 根节点：代价为 n，有 2 个子节点（T (n/3) 和 T (2n/3)）。
- 第 1 层：代价分别为 n/3 和 2n/3，总代价为 n。
- 第 2 层：代价分别为 (n/3)/3, (n/3)・2/3, (2n/3)/3, (2n/3)・2/3，总代价为 n。
- ...
- 每一层的总代价均为 n。
确定树的深度：最右边的路径（每次乘以 2/3）最深，深度为 log₃/₂n = O (log n)。
求和：

T(n) = n·O(log n) = O(n log n)。

流程图

4.5 用主方法求解递归式

方法概述

主方法（Master Method）适用于求解形如以下形式的递归式：

T(n) = aT(n/b) + f(n)

其中：

a ≥ 1（子问题的数量）
b > 1（每个子问题的规模是原问题的 1/b）
f (n) 是渐近正函数（代表分解和合并的代价）

主方法通过比较 f (n) 与 n^log_b a 的大小关系，直接给出递归式的解：

情况 1：若 f (n) = O (n^log_b a - ε) 对于某个 ε > 0 成立，则 T (n) = Θ(n^log_b a)。
情况 2：若 f (n) = Θ(n^log_b a log^k n) 对于某个 k ≥ 0 成立，则 T (n) = Θ(n^log_b a log^{k+1} n)。
情况 3：若 f (n) = Ω(n^log_b a + ε) 对于某个 ε > 0 成立，且存在常数 c < 1 使得对于足够大的 n，有 a・f (n/b) ≤ c・f (n)（正则条件），则 T (n) = Θ(f (n))。

示例解析

示例 1：T(n) = 9T(n/3) + n

a=9, b=3, log_b a = log₃9 = 2
f (n) = n = O (n²⁻¹)，满足情况 1
因此，T (n) = Θ(n²)

示例 2：T(n) = T(2n/3) + 1

a=1, b=3/2, log_b a = 0
f (n) = 1 = Θ(n⁰ log⁰ n)，满足情况 2（k=0）
因此，T (n) = Θ(log n)

示例 3：T(n) = 3T(n/4) + n log n

a=3, b=4, log_b a ≈ 0.793
f (n) = n log n = Ω(n⁰・⁷⁹³ + ε)（取 ε=0.2），且验证正则条件：
a・f (n/b) = 3・(n/4) log (n/4) ≤ 3/4・n log n ≤ c・f (n)（取 c=3/4 < 1）
满足情况 3，因此 T (n) = Θ(n log n)

示例 4：T(n) = 2T(n/2) + n log n

a=2, b=2, log_b a = 1
f (n) = n log n = Θ(n¹ log¹ n)，满足情况 2（k=1）
因此，T (n) = Θ(n log² n)

注意事项

主方法的三种情况是互斥的，并非所有递归式都能适用主方法。
情况 3 中的正则条件是必要的，若不满足则无法应用情况 3。
当 f (n) 与 n^log_b a 的大小关系介于情况 1 和情况 2 之间，或介于情况 2 和情况 3 之间时，主方法不适用。

4.6 证明主定理

4.6.1 对 b 的幂证明主定理

为了简化证明，先假设 n 是 b 的幂，即 n = b^k，其中 k 是整数。此时，n/b = b^{k-1}，n/b² = b^{k-2}，以此类推。

递归式展开 ：

T(n) = aT(n/b) + f(n)

= a(aT(n/b²) + f(n/b)) + f(n)

= a²T(n/b²) + a f(n/b) + f(n)

= ...

= a^k T(1) + Σ_{i=0}^{k-1} a^i f(n/b^i)

其中，k = log_b n，a^k = a^{log_b n} = n^{log_b a}（由换底公式：a^{log_b n} = n^{log_b a}）。

因此，T (n) = Θ(n^{log_b a}) + Σ_{i=0}^{k-1} a^i f (n/b^i)。

接下来，通过分析和式 Σ_{i=0}^{k-1} a^i f (n/b^i) 来证明三种情况：

情况 1 ：若 f (n) = O (n^log_b a - ε)，则存在常数 c > 0 和 ε > 0，使得 f (n) ≤ c n^log_b a - ε。

代入和式得：

Σ a^i f (n/b^i) ≤ c Σ a^i (n/b^i)^{log_b a - ε}

= c n^{log_b a - ε} Σ a^i / (b^{i (log_b a - ε)})

= c n^{log_b a - ε} Σ (a / b^{log_b a - ε})^i

= c n^{log_b a - ε} Σ (b^ε)^i （因为 a = b^{log_b a}）

这是一个公比为 b^ε > 1 的等比数列，和为 O (b^{ε k}) = O (n^ε)。

因此，Σ = O (n^{log_b a - ε}・n^ε) = O (n^{log_b a})，故 T (n) = Θ(n^{log_b a})。
情况 2 ：若 f (n) = Θ(n^log_b a log^k n)，则：

Σ a^i f (n/b^i) = Θ(Σ a^i (n/b^i)^{log_b a} log^k (n/b^i))

= Θ(n^{log_b a} Σ log^k (n/b^i))

当 k=0 时，Σ log^0 (n/b^i) = Σ 1 = k = Θ(log n)，故 Σ = Θ(n^{log_b a} log n)。

对于 k > 0，可通过归纳法证明 Σ = Θ(n^{log_b a} log^{k+1} n)。

因此，T (n) = Θ(n^{log_b a} log^{k+1} n)。
情况 3 ：若 f (n) = Ω(n^log_b a + ε) 且满足正则条件，则：

由正则条件 a f (n/b) ≤ c f (n)，可得 a^i f (n/b^i) ≤ c^i f (n)。

因此，Σ a^i f (n/b^i) ≤ f (n) Σ c^i = O (f (n))（因为 c < 1，等比级数和有界）。

同时，Σ a^i f (n/b^i) ≥ f (n)（第一项），故 Σ = Θ(f (n))。

因此，T (n) = Θ(f (n))。

4.6.2 向下取整和向上取整

实际中，n 不一定是 b 的幂，此时 n/b 可能需要向下取整（⌊n/b⌋）或向上取整（⌈n/b⌉）。可以证明，这种取整操作不会改变递归式解的渐近阶。

例如，对于递归式 T (n) = a T (⌊n/b⌋) + f (n)，可以证明：

存在常数 k，使得⌊n/b^i⌋ ≥ n/b^i - k。
通过适当调整常数，可证明其解与 n 是 b 的幂时的解具有相同的渐近阶。

因此，主定理对于 n 不是 b 的幂的情况同样成立。

思考题

最大子数组问题的变形：如何求解最大子数组问题的非递归版本（如 Kadane 算法）？其时间复杂度是多少？
递归式求解：使用代入法、递归树方法和主方法求解以下递归式：
- T(n) = 4T(n/2) + n
- T(n) = 4T(n/2) + n²
- T(n) = 4T(n/2) + n³
Strassen 算法的优化：Strassen 算法的时间复杂度是 O (n^2.807)，是否存在时间复杂度更低的矩阵乘法算法？目前的最优结果是什么？
分治策略的应用：除了本章介绍的问题，分治策略还可以应用于哪些问题？试举例说明其分治思路。

本章注记

分治策略是算法设计中的一种重要思想，其核心是将问题分解为更小的子问题，递归求解后合并结果。
最大子数组问题和 Strassen 矩阵乘法是分治策略的经典应用，分别将时间复杂度从 O (n²) 和 O (n³) 降低到了 O (n log n) 和 O (n^2.807)。
递归式的求解是分析分治算法复杂度的关键，代入法、递归树方法和主方法是三种常用的求解工具，其中主方法最为高效，但适用范围有限。
主定理的证明过程展示了递归式展开和求和的技巧，有助于深入理解分治算法的复杂度分析。

分治策略在排序算法（如归并排序、快速排序）、查找算法（如二分查找）、计算几何（如最近点对问题）等领域都有广泛应用，是每个程序员必须掌握的基本算法思想。

希望本文能帮助读者深入理解分治策略及其应用。文中的代码均经过测试，可以直接编译运行，读者可以动手实践，进一步体会分治策略的精髓。如有疑问或建议，欢迎在评论区留言讨论！