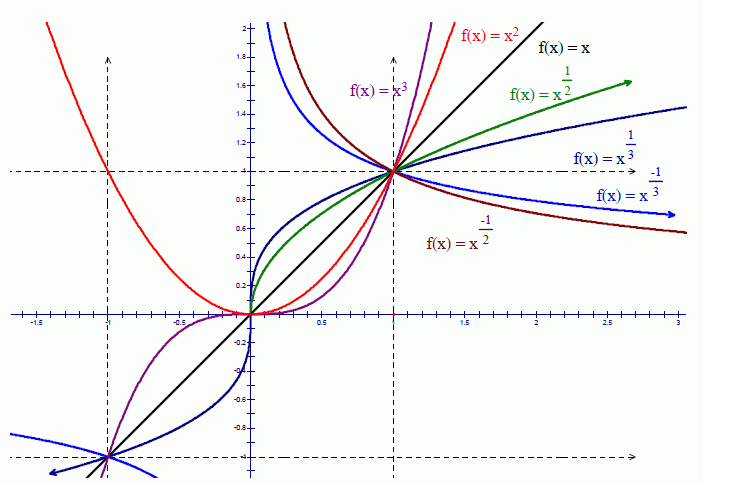
大家好!今天我们来学习《算法导论》的第 3 章 ------ 函数的增长。这一章内容是算法分析的基础,帮助我们理解当输入规模增大时,算法的运行时间或空间需求如何变化。掌握这些知识,能让我们更好地评估和比较不同算法的效率。

3.1 渐近记号
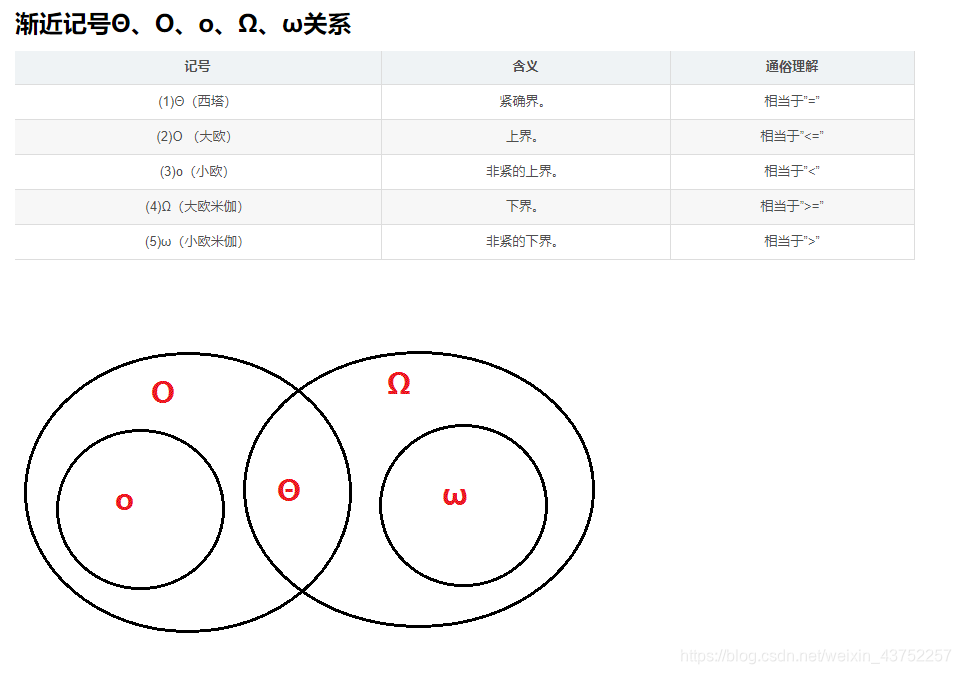
在算法分析中,我们常常关注当输入规模 n 趋向于无穷大时,算法的运行时间如何增长。渐近记号就是描述这种增长趋势的数学工具。常用的渐近记号有:O(大 O)、Ω(大 Ω)、Θ(大 Θ)、o(小 o)和 ω(小 ω)。
3.1.1 O 记号(上界)
O 记号表示一个函数的渐近上界。如果存在正常数 c 和 n₀,使得当 n ≥ n₀时,有 f (n) ≤ c・g (n),则称 f (n) = O (g (n))。
简单来说,O (g (n)) 表示函数 f (n) 的增长速度不会超过 g (n) 的某个常数倍。
代码示例:O (n) 时间复杂度的算法(线性查找)
#include <iostream>
#include <vector>
// 线性查找:在数组中查找目标值,返回其索引,未找到返回-1
// 时间复杂度:O(n),n为数组元素个数
int linearSearch(const std::vector<int>& arr, int target) {
// 遍历数组中的每个元素
for (int i = 0; i < arr.size(); ++i) { // 最多执行n次
if (arr[i] == target) { // 每次执行常数时间
return i;
}
}
return -1;
}
int main() {
std::vector<int> arr = {3, 1, 4, 1, 5, 9, 2, 6};
int target = 5;
int result = linearSearch(arr, target);
if (result != -1) {
std::cout << "找到目标值 " << target << ",索引为:" << result << std::endl;
} else {
std::cout << "未找到目标值 " << target << std::endl;
}
return 0;
}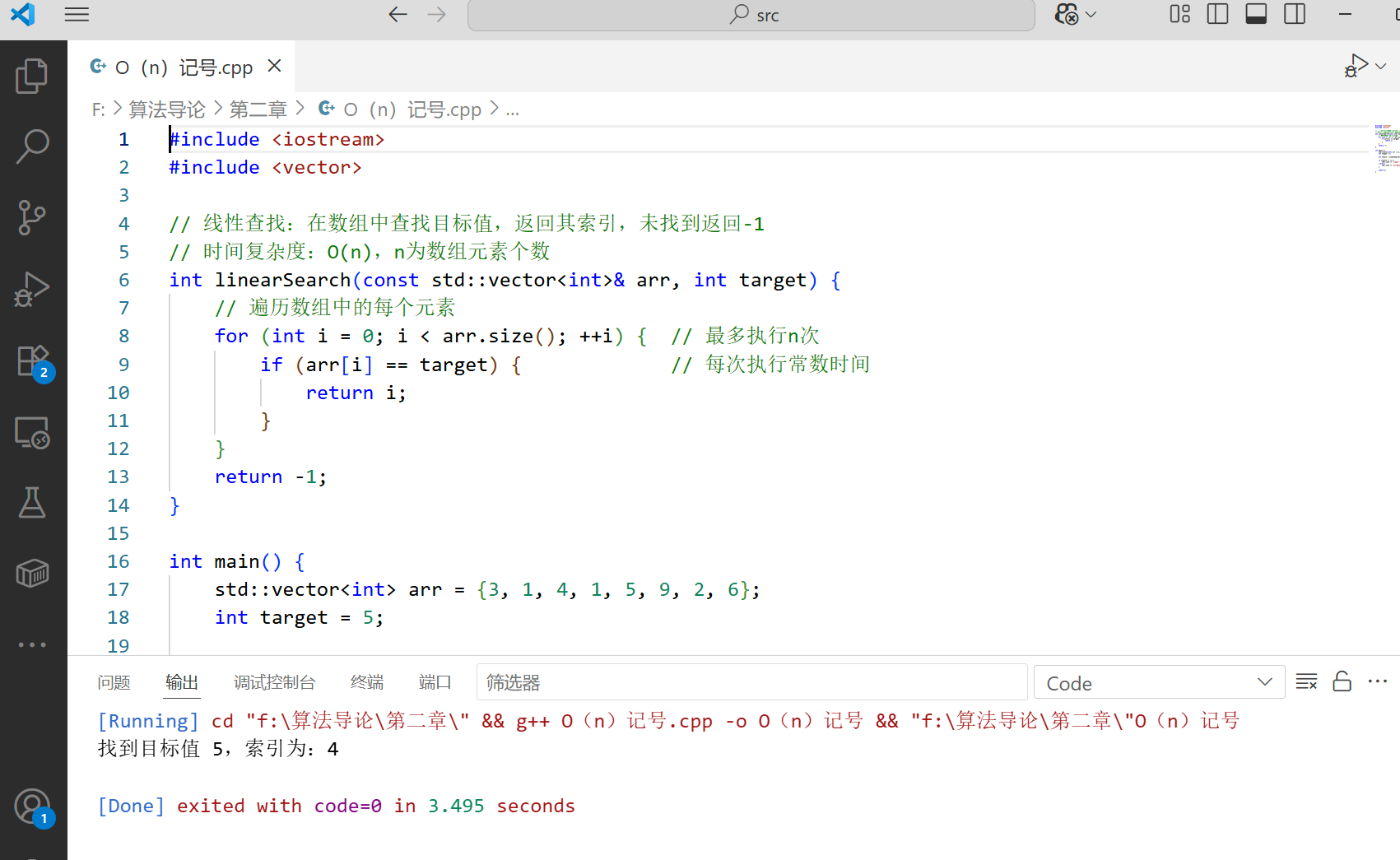
代码说明 :线性查找算法在最坏情况下需要遍历整个数组,因此时间复杂度为 O (n)。这意味着当数组规模 n 增大时,算法的运行时间最多以线性速度增长。
3.1.2 Ω 记号(下界)
Ω 记号表示一个函数的渐近下界。如果存在正常数 c 和 n₀,使得当 n ≥ n₀时,有 f (n) ≥ c・g (n),则称 f (n) = Ω(g (n))。
Ω(g (n)) 表示函数 f (n) 的增长速度不会低于 g (n) 的某个常数倍。
代码示例:Ω(n) 时间复杂度的算法
#include <iostream>
#include <vector>
// 检查数组中是否存在负数,存在返回true,否则返回false
// 时间复杂度:Ω(n),在最好情况下(数组第一个元素就是负数)为O(1)
// 但在最坏情况下(数组中没有负数或最后一个元素是负数)为O(n)
// 因此,我们可以说该算法的时间复杂度是Ω(n),因为它至少需要检查到第一个负数才能停止
bool hasNegativeNumber(const std::vector<int>& arr) {
for (int num : arr) { // 最少执行1次(如果第一个元素是负数),最多执行n次
if (num < 0) {
return true;
}
}
return false;
}
int main() {
std::vector<int> arr1 = {1, 2, 3, -4, 5};
std::vector<int> arr2 = {1, 2, 3, 4, 5};
std::cout << "arr1 是否包含负数:" << (hasNegativeNumber(arr1) ? "是" : "否") << std::endl;
std::cout << "arr2 是否包含负数:" << (hasNegativeNumber(arr2) ? "是" : "否") << std::endl;
return 0;
}
代码说明:这个算法用于检查数组中是否存在负数。在最坏情况下(数组中没有负数),算法需要遍历整个数组,因此我们可以确定它的时间复杂度下界是 Ω(n)。
3.1.3 Θ 记号(紧界)
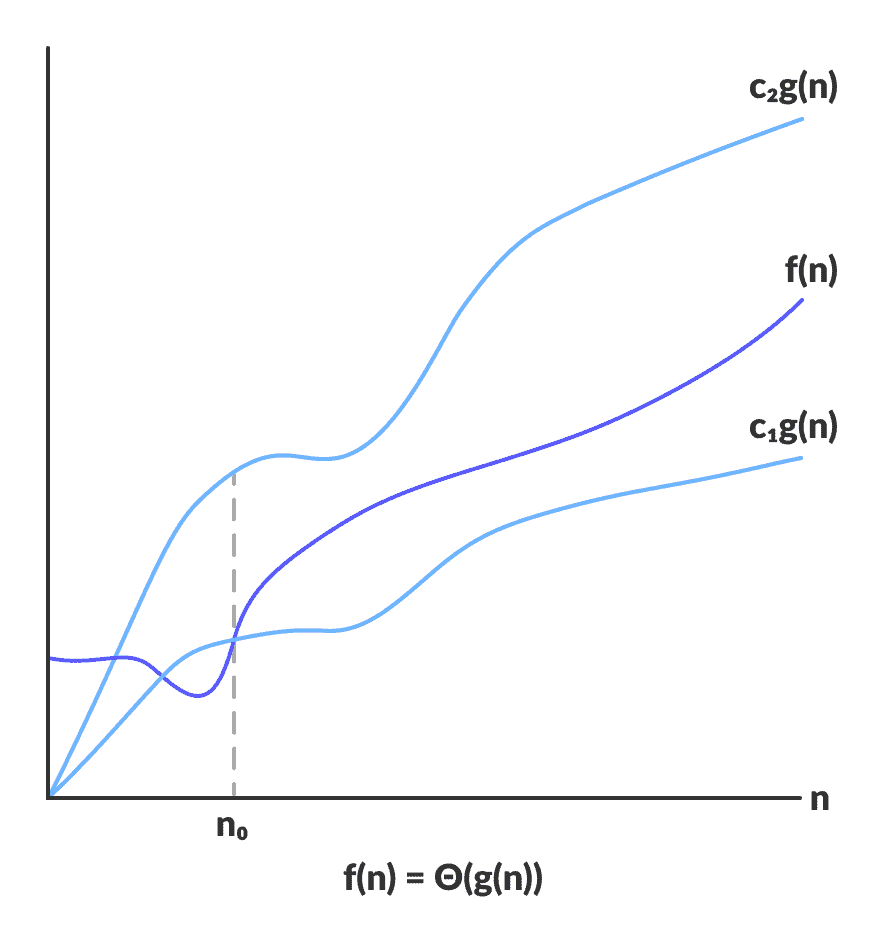
Θ 记号表示一个函数的渐近紧界。如果存在正常数 c₁、c₂和 n₀,使得当 n ≥ n₀时,有 c₁・g (n) ≤ f (n) ≤ c₂・g (n),则称 f (n) = Θ(g (n))。
Θ(g (n)) 表示函数 f (n) 的增长速度与 g (n) 相当,既是上界也是下界。
代码示例:Θ(n) 时间复杂度的算法
#include <iostream>
#include <vector>
// 计算数组中所有元素的和
// 时间复杂度:Θ(n),无论输入如何,都需要遍历整个数组
int sumOfArray(const std::vector<int>& arr) {
int sum = 0;
for (int num : arr) { // 必须执行n次
sum += num; // 每次执行常数时间
}
return sum;
}
int main() {
std::vector<int> arr = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10};
std::cout << "数组元素的和为:" << sumOfArray(arr) << std::endl;
return 0;
}
代码说明:计算数组元素和的算法,无论输入是什么,都必须遍历整个数组一次,因此它的时间复杂度是 Θ(n),既是上界也是下界。
3.1.4 o 记号和 ω 记号(非紧界)
- o 记号:表示比 O 记号更严格的上界,即 f (n) 的增长速度比 g (n) 慢。
- ω 记号:表示比 Ω 记号更严格的下界,即 f (n) 的增长速度比 g (n) 快。
3.1.5 综合案例:不同时间复杂度的算法比较
下面我们通过代码来比较几种常见时间复杂度的算法:
cpp
#include <iostream>
#include <vector>
#include <chrono> // 用于计时
#include <algorithm> // 新增:包含sort函数所需的头文件
using namespace std;
using namespace chrono;
// O(1):常数时间算法
void constantTimeAlgorithm() {
int x = 5;
int y = 10;
int sum = x + y; // 单一操作,与输入规模无关
}
// O(log n):对数时间算法(二分查找)
bool binarySearch(const vector<int>& arr, int target) {
int left = 0;
int right = arr.size() - 1;
while (left <= right) {
int mid = left + (right - left) / 2; // 避免溢出
if (arr[mid] == target) {
return true;
} else if (arr[mid] < target) {
left = mid + 1;
} else {
right = mid - 1;
}
// 每次迭代,搜索空间大约减半
}
return false;
}
// O(n):线性时间算法
int linearSum(const vector<int>& arr) {
int sum = 0;
for (int num : arr) { // 遍历所有元素
sum += num;
}
return sum;
}
// O(n log n):线性对数时间算法(简化的归并排序思想)
void mergeSort(vector<int>& arr, int left, int right) {
if (left < right) {
int mid = left + (right - left) / 2;
// 递归排序左右两半
mergeSort(arr, left, mid);
mergeSort(arr, mid + 1, right);
// 合并两个已排序的子数组
vector<int> temp(right - left + 1);
int i = left, j = mid + 1, k = 0;
while (i <= mid && j <= right) {
if (arr[i] <= arr[j]) {
temp[k++] = arr[i++];
} else {
temp[k++] = arr[j++];
}
}
while (i <= mid) temp[k++] = arr[i++];
while (j <= right) temp[k++] = arr[j++];
for (i = left, k = 0; i <= right; i++, k++) {
arr[i] = temp[k];
}
}
}
// O(n²):平方时间算法(冒泡排序)
void bubbleSort(vector<int>& arr) {
int n = arr.size();
for (int i = 0; i < n - 1; i++) { // 外层循环:n-1次
for (int j = 0; j < n - i - 1; j++) { // 内层循环:最多n-1次
if (arr[j] > arr[j + 1]) {
swap(arr[j], arr[j + 1]); // 交换元素
}
}
}
}
int main() {
// 创建一个较大的数组用于测试
int n = 10000;
vector<int> arr(n);
for (int i = 0; i < n; i++) {
arr[i] = n - i; // 逆序排列,使排序算法处于最坏情况
}
// 测试O(1)算法
auto start = high_resolution_clock::now();
constantTimeAlgorithm();
auto end = high_resolution_clock::now();
duration<double, micro> constantTime = end - start;
cout << "O(1) 算法时间: " << constantTime.count() << " 微秒" << endl;
// 测试O(log n)算法(先排序数组才能用二分查找)
vector<int> sortedArr = arr;
sort(sortedArr.begin(), sortedArr.end()); // 现在可以正常使用sort函数了
start = high_resolution_clock::now();
bool found = binarySearch(sortedArr, n / 2);
end = high_resolution_clock::now();
duration<double, micro> logTime = end - start;
cout << "O(log n) 算法时间: " << logTime.count() << " 微秒, 是否找到: " << (found ? "是" : "否") << endl;
// 测试O(n)算法
start = high_resolution_clock::now();
int sum = linearSum(arr);
end = high_resolution_clock::now();
duration<double, micro> linearTime = end - start;
cout << "O(n) 算法时间: " << linearTime.count() << " 微秒, 和为: " << sum << endl;
// 测试O(n log n)算法
vector<int> arr1 = arr;
start = high_resolution_clock::now();
mergeSort(arr1, 0, n - 1);
end = high_resolution_clock::now();
duration<double, micro> nLogNTime = end - start;
cout << "O(n log n) 算法时间: " << nLogNTime.count() << " 微秒" << endl;
// 测试O(n²)算法
int smallN = 1000; // 注意:如果太大,程序会运行很久
vector<int> smallArr(smallN);
for (int i = 0; i < smallN; i++) {
smallArr[i] = smallN - i;
}
start = high_resolution_clock::now();
bubbleSort(smallArr);
end = high_resolution_clock::now();
duration<double, micro> squareTime = end - start;
cout << "O(n²) 算法时间 (n=" << smallN << "): " << squareTime.count() << " 微秒" << endl;
return 0;
}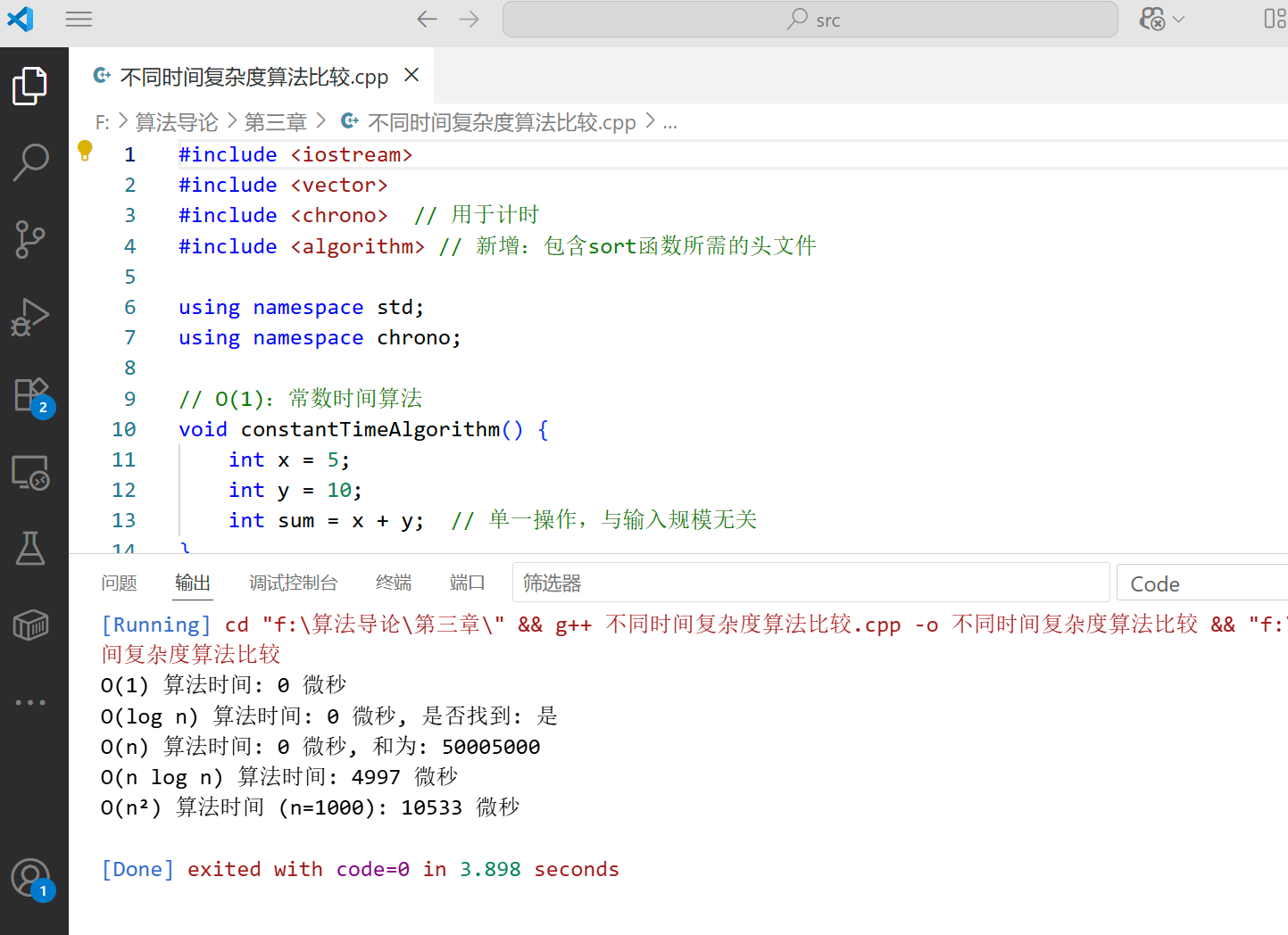
代码说明:这个程序比较了五种不同时间复杂度的算法的运行时间。通过实际运行,我们可以直观地看到,当输入规模增大时,不同时间复杂度的算法运行时间增长速度差异很大。特别是 O (n²) 的算法,当 n 增大时,运行时间会急剧增加。
3.2 标准记号与常用函数
在算法分析中,我们经常会遇到一些特定的函数和记号。熟悉它们有助于我们更好地分析算法复杂度。
3.2.1 基本记号
-
单调性:如果 m ≤ n 蕴含 f (m) ≤ f (n),则函数 f (n) 是单调递增的;如果 m < n 蕴含 f (m) < f (n),则函数 f (n) 是严格单调递增的。类似地可以定义单调递减和严格单调递减。
-
取整函数:
- floor (x):小于或等于 x 的最大整数
- ceil (x):大于或等于 x 的最小整数
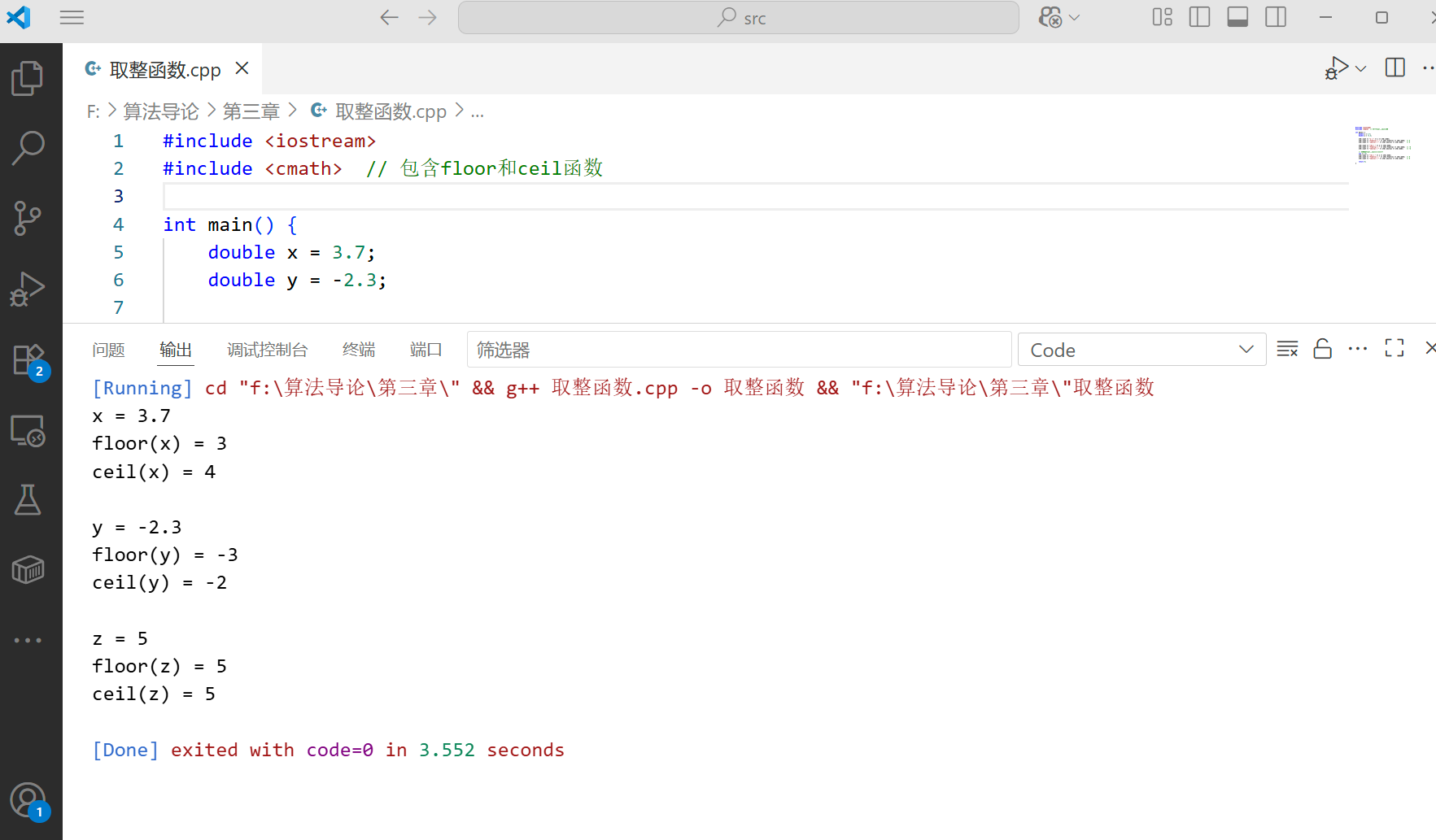
代码示例:取整函数
#include <iostream>
#include <cmath> // 包含floor和ceil函数
int main() {
double x = 3.7;
double y = -2.3;
std::cout << "x = " << x << std::endl;
std::cout << "floor(x) = " << std::floor(x) << std::endl; // 3
std::cout << "ceil(x) = " << std::ceil(x) << std::endl; // 4
std::cout << "\ny = " << y << std::endl;
std::cout << "floor(y) = " << std::floor(y) << std::endl; // -3
std::cout << "ceil(y) = " << std::ceil(y) << std::endl; // -2
// 整数的floor和ceil都是其本身
int z = 5;
std::cout << "\nz = " << z << std::endl;
std::cout << "floor(z) = " << std::floor(z) << std::endl; // 5
std::cout << "ceil(z) = " << std::ceil(z) << std::endl; // 5
return 0;
}3.2.2 常用函数
-
多项式函数:f(n) = aₖnᵏ + ... + a₁n + a₀
- 多项式的阶数是最高次项的次数
- 对于正系数多项式,其渐近复杂度是 Θ(nᵏ),其中 k 是最高次项的次数
-
指数函数:f (n) = aⁿ,其中 a > 0
- 指数函数的增长速度快于任何多项式函数
- 例如:2ⁿ增长比 n³ 快得多
-
对数函数:f (n) = logₐn,其中 a > 0 且 a ≠ 1
- 对数函数的增长速度慢于任何多项式函数
- 不同底数的对数函数之间只有常数因子的差别,因此通常写作 log n,不特别指明底数
-
阶乘函数:f(n) = n!
- 阶乘函数的增长速度快于指数函数
- n! = n × (n-1) × ... × 1
-
求和公式:
- Σₖ₌₁ⁿ k = n (n+1)/2 (前 n 个正整数之和)
- Σₖ₌₀ⁿ rᵏ = (rⁿ⁺¹ - 1)/(r - 1) (几何级数求和)
代码示例:常用函数的实现与比较
#include <iostream>
#include <vector>
#include <cmath>
#include <iomanip> // 用于设置输出精度
using namespace std;
// 计算阶乘
long long factorial(int n) {
if (n <= 1) return 1;
long long result = 1;
for (int i = 2; i <= n; i++) {
result *= i;
}
return result;
}
// 计算几何级数和: sum = r^0 + r^1 + ... + r^n
double geometricSeriesSum(double r, int n) {
if (r == 1) return n + 1; // 特殊情况:公比为1时,和为n+1
return (pow(r, n + 1) - 1) / (r - 1);
}
int main() {
// 比较不同函数在n增大时的取值
cout << setw(5) << "n"
<< setw(15) << "log2(n)"
<< setw(10) << "n"
<< setw(15) << "n log2(n)"
<< setw(10) << "n^2"
<< setw(15) << "2^n"
<< setw(15) << "n!" << endl;
cout << string(90, '-') << endl;
for (int n = 1; n <= 15; n++) {
double logVal = (n == 0) ? 0 : log2(n);
double nLogN = (n == 0) ? 0 : n * log2(n);
long long squareVal = (long long)n * n;
long long expVal = (n <= 30) ? (1LL << n) : 0; // 2^n,n太大时会溢出
long long factVal = (n <= 20) ? factorial(n) : 0; // n!,n太大时会溢出
cout << setw(5) << n
<< setw(15) << fixed << setprecision(2) << logVal
<< setw(10) << n
<< setw(15) << fixed << setprecision(2) << nLogN
<< setw(10) << squareVal;
// 处理可能的溢出情况
if (n <= 30) cout << setw(15) << expVal;
else cout << setw(15) << "溢出";
if (n <= 20) cout << setw(15) << factVal;
else cout << setw(15) << "溢出";
cout << endl;
}
// 演示几何级数求和
cout << "\n几何级数求和示例:" << endl;
double r = 2.0;
for (int n = 1; n <= 10; n++) {
cout << "sum(2^0 + 2^1 + ... + 2^" << n << ") = "
<< geometricSeriesSum(r, n) << endl;
}
return 0;
}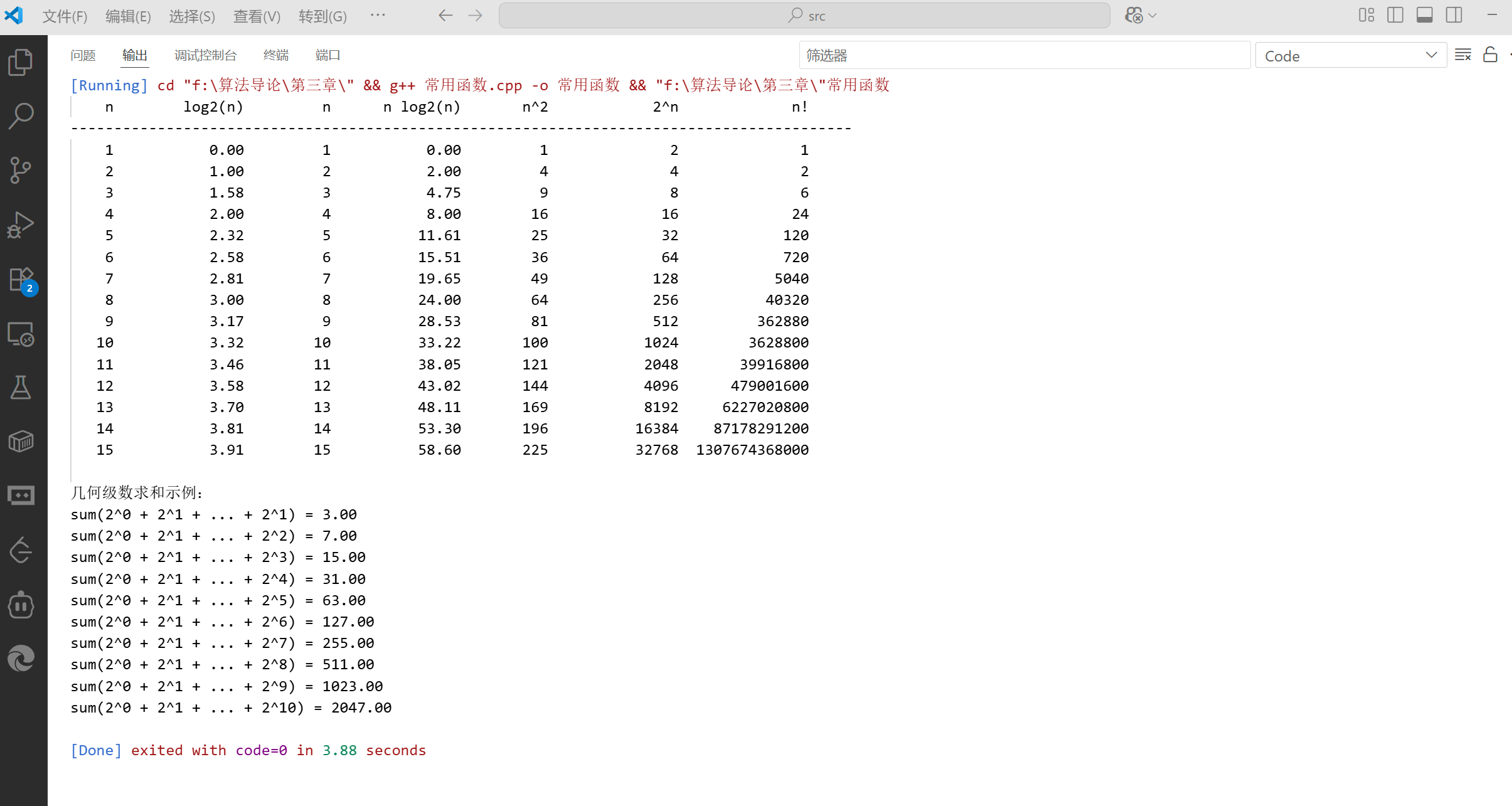
代码说明:这段代码展示了各种常用函数的实现和它们在 n 增大时的取值变化。从输出结果可以清晰地看到不同函数的增长速度差异,尤其是阶乘函数和指数函数的增长速度非常快,很快就会导致整数溢出。
思考题
-
分析以下代码的时间复杂度:
void mystery(int n) {
int i = 1;
while (i <= n) {
for (int j = 1; j <= i; j++) {
cout << "*";
}
cout << endl;
i *= 2;
}
} -
证明对于任意正整数 n,有 n! = o (nⁿ),即 n! 的增长速度严格慢于 nⁿ。
-
比较 log (n!) 和 n log n 的增长速度,它们是否是同一数量级的?
-
分析快速排序算法的平均时间复杂度为什么是 O (n log n)。
参考答案提示:
- 时间复杂度为 O (n)。虽然有嵌套循环,但外循环的迭代次数是 log n,内循环的总执行次数是 1 + 2 + 4 + ... + n = 2n - 1 = O (n)。
- 可以通过斯特林公式 (n! ≈ nⁿe⁻ⁿ√(2πn)) 来证明,或者通过数学归纳法。
- 根据斯特林公式,log (n!) 与 n log n 是同一数量级的,即 log (n!) = Θ(n log n)。
- 快速排序在平均情况下,每次划分将数组分为大致相等的两部分,递归深度为 log n,每一层的总操作时间为 O (n),因此总时间复杂度为 O (n log n)。
本章注记
- 渐近分析是算法分析的核心工具,它帮助我们忽略常数因子和低阶项,专注于算法在输入规模增大时的增长趋势。
- 掌握 O、Ω、Θ 等渐近记号的定义和使用场景,是进行算法分析的基础。
- 熟悉各种常用函数的增长特性,能帮助我们快速判断算法的效率和 scalability。
- 在实际应用中,我们不仅要关注算法的渐近复杂度,还要考虑常数因子、空间复杂度以及实际输入的分布情况。
渐近分析为我们提供了一种客观比较不同算法效率的框架,是每个程序员和算法设计者必须掌握的基础知识。在后续章节中,我们将大量使用本章介绍的概念和工具来分析各种算法的复杂度。

希望这篇笔记能帮助大家更好地理解《算法导论》第 3 章的内容。如果有任何疑问或建议,欢迎在评论区留言讨论!