MOPSO实现无人机多目标路径规划（Matlab完整源码和数据）

---

一、MOPSO算法核心原理

MOPSO（多目标粒子群优化算法）通过模拟鸟群觅食行为，在搜索空间中寻找满足多个冲突目标的Pareto最优解集。其核心流程包括：

1. 粒子初始化：随机生成粒子群，每个粒子代表一条候选路径，包含位置（路径坐标序列）和速度（路径调整方向）信息。
2. 适应度评价：计算路径的多个目标函数值（如路径长度、能耗、安全距离等）。
3. 非支配排序 ：构建外部档案（External Archive, EA）存储当前非支配解，通过网格密度法或拥挤距离法维护档案多样性。
   
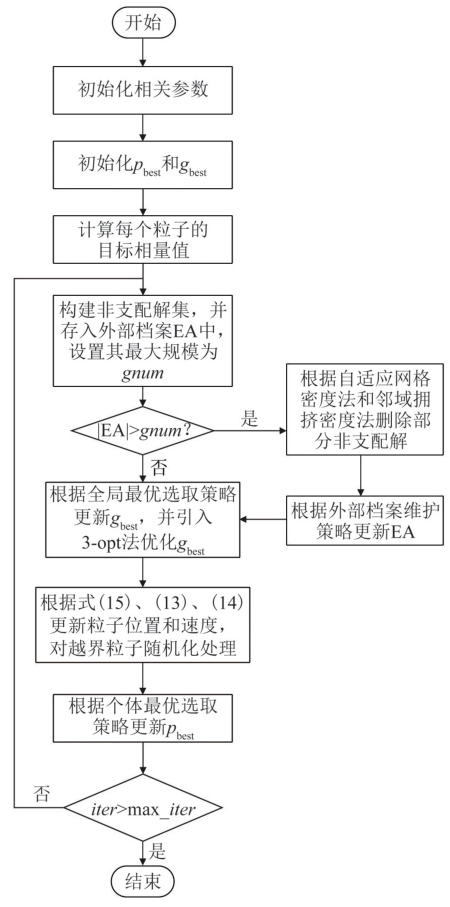
4. 全局/个体最优解更新：从EA中选择引导粒子，结合3-opt局部优化策略提升解质量。
5. 速度与位置更新：通过公式迭代调整粒子状态，直至满足终止条件。

---

二、无人机路径规划多目标建模

1. 目标函数设计

目标函数需综合考虑以下因素（以三维路径为例）：

% 示例目标函数（需根据实际需求调整权重）
function [f1, f2, f3] = fitness(path)
    % 目标1：路径总长度（欧氏距离累加）
    f1 = sum(sqrt(diff(path.x).^2 + diff(path.y).^2 + diff(path.z).^2));
    
    % 目标2：最小安全距离（与障碍物的最近距离）
    f2 = min(calculateObstacleDistance(path)); 
    
    % 目标3：能耗模型（与高度变化相关）
    f3 = sum(abs(diff(path.z)) * energy_per_meter); 
end

• 权重法 ：线性加权组合多个目标（如F = w1*f1 + w2*f2 + w3*f3）。
• Pareto法：独立优化各目标，通过非支配解集提供多种权衡方案。

2. 关键约束条件

约束类型	处理方法
飞行高度	限制z坐标范围，超限时施加惩罚项（如penalty = γ*(h_actual - h_max)）
转弯半径	通过Dubins曲线平滑路径，确保符合无人机机动能力
障碍物避碰	使用栅格法建模环境，检测路径段与障碍物相交性
能量限制	最大路径长度约束，超限粒子直接淘汰

---

三、障碍物建模与避障策略

1. 环境建模方法

• 栅格化处理：将三维空间离散化为立方体网格，标记障碍物栅格（0/1矩阵）。
• 不规则障碍物：采用凸化填充法将凹多边形分解为多个凸多边形，简化碰撞检测。

% 示例：障碍物栅格地图生成
map.resolution = 0.5; % 栅格粒度（km）
map.obstacles = load('obstacle_coordinates.txt'); 
gridMap = createGrid3D(map.obstacles, map.resolution);

2. 避障检测算法

• 射线法：判断路径段是否与障碍物边界相交。
• 安全裕度：设置缓冲区（如0.4km），路径需与障碍物保持最小距离。

function isCollision = checkCollision(path, gridMap, safeMargin)
    for i = 1:length(path.x)-1
        segment = [path.x(i:i+1), path.y(i:i+1), path.z(i:i+1)];
        if rayCast(segment, gridMap, safeMargin)
            isCollision = true;
            return;
        end
    end
    isCollision = false;
end

---

四、MOPSO算法Matlab实现框架

1. 主程序结构

% MOPSO参数设置
nParticles = 100;    % 粒子数量
maxIter = 200;       % 最大迭代次数
w = 0.7;             % 惯性权重
c1 = 1.5; c2 = 1.5; % 学习因子
gridSize = [50,50];  % 外部档案网格维度

% 初始化粒子群
particles = initializeParticles(nParticles, map);
archive = [];        % 外部档案

for iter = 1:maxIter
    % 计算适应度并更新非支配解
    fitnessValues = evaluateFitness(particles);
    [nonDominated, dominated] = fastNonDominatedSort(fitnessValues);
    archive = updateArchive([archive; particles(nonDominated)], gridSize);
    
    % 选择全局引导粒子（基于网格密度）
    gBest = selectGlobalBest(archive);
    
    % 更新粒子速度与位置
    particles = updateParticles(particles, gBest, w, c1, c2);
    
    % 应用3-opt局部优化（提升路径平滑性）
    particles = apply3Opt(particles, map);
    
    % 越界处理与约束修复
    particles = repairParticles(particles, map);
end

% 输出Pareto最优解集
plotParetoFront(archive);

2. 关键函数实现

• 非支配排序：采用NSGA-II的快速非支配排序算法，复杂度O(MN²)。
• 外部档案管理：使用自适应网格法维护解集多样性，删除密集区域冗余解。
• 3-opt优化：对全局最优解进行局部路径优化，减少不必要的转折点。

---

五、Pareto前沿可视化

通过Matplotlib或Matlab内置绘图工具展示多目标优化结果：

function plotParetoFront(archive)
    f1 = [archive.f1];
    f2 = [archive.f2];
    scatter(f1, f2, 'filled');
    xlabel('路径长度 (km)'); 
    ylabel('安全距离 (m)');
    title('MOPSO Pareto前沿');
    grid on;
end

---

六、完整代码获取：私信博主回复MOPSO实现无人机多目标路径规划（Matlab完整源码和数据）