叠甲，微实验系列主要是笔者以MATLAB为主要工具，多使用AI编写代码，对数字音频信号进行各种操作的尝试、以及对声音信号的频域与时域特征性质进行的各种探索，日志性较强，教程性较低，相对于笔者所写得【手把手】和【超详细】教程或者科普系列来说更加粗糙随意，介意者慎入。不定期更新。
前情提要~
【微实验】圆周运动的正弦信号发生仿真及其衍生（一）-CSDN博客
【微实验】圆周运动的正弦信号发生仿真及其衍生（二）-CSDN博客
这两篇文章中，我们定义了"扒谱机变换"和它的逆变换，即把极坐标里的轨迹形状转化成能被听见的声音波形。
具体来说，就是先确定极坐标里极径随角度变化的规律，也就是极径函数，再结合一个随时间均匀变化的幅角，最终获取声音的波形。
第一篇中给的例子里------
- 圆形对应的极径是一个固定的常数，不随角度改变。当角度随时间均匀增加时，对应的波形就是标准的正弦波，只有一个基频。
- 心形线的极径函数是用一个常数乘以（1加上角度的余弦值）。这使得极径会随着角度的变化而有规律地增减，轨迹呈现出心形。这样的函数转化成波形时，会在正弦波的基础上叠加一个与角度余弦相关的变化，让波形产生脉动，听起来除了基频，还会有二次谐波的成分。
- 玫瑰线的极径函数是常数乘以角度整数倍的余弦值，这里的整数决定了玫瑰花瓣的数量。比如当这个整数是3时，极径就跟着3倍角度的余弦值变化，轨迹是3瓣玫瑰的形状。对应的波形会因为这种多倍角度的变化，产生基频之外的更多谐波，谐波的频率和这个整数相关，让声音的频谱更丰富。
- 椭圆的极径函数相对复杂些，是用椭圆半长轴和半短轴的乘积，除以一个由角度的正弦和余弦值组成的平方根式子。这保证了极坐标下的轨迹是椭圆，极径会随着角度变化但保持椭圆的形状。转化出的波形接近正弦波，但幅值会有轻微的波动，谐波较少，听起来比较平滑。
- 像奇形怪状的"派大星函数"这样的复杂闭合曲线，极径函数是由多个部分组合而成的。它包含一个常数项，一个和5倍角度余弦相关的项，还有一个由角度正弦、余弦组成的分式项。这样的组合让极径随角度的变化变得很不规则，轨迹也是不规则的闭合曲线。对应的波形就会非常复杂，包含基频、5倍频以及更多高次谐波和组合出来的频率，听起来音色丰富且独特。
总的来说，这些极径函数就像是不同的"模具"，通过扒谱机变换，能把它们各自的形状特点转化成不同的声音波形，简单的函数对应纯净或较少谐波的声音，复杂的函数则对应谐波丰富、音色多样的声音。
为了更加贴合声音实验，今天小编压榨AI请他生成了更多的极坐标函数，然后编写代码生成基频为440Hz波形，绘图、播放然后存储到工作路径中。
（因为代码已经验证无误，为提高效率，不再进行动画仿真，而是直接给出结果）
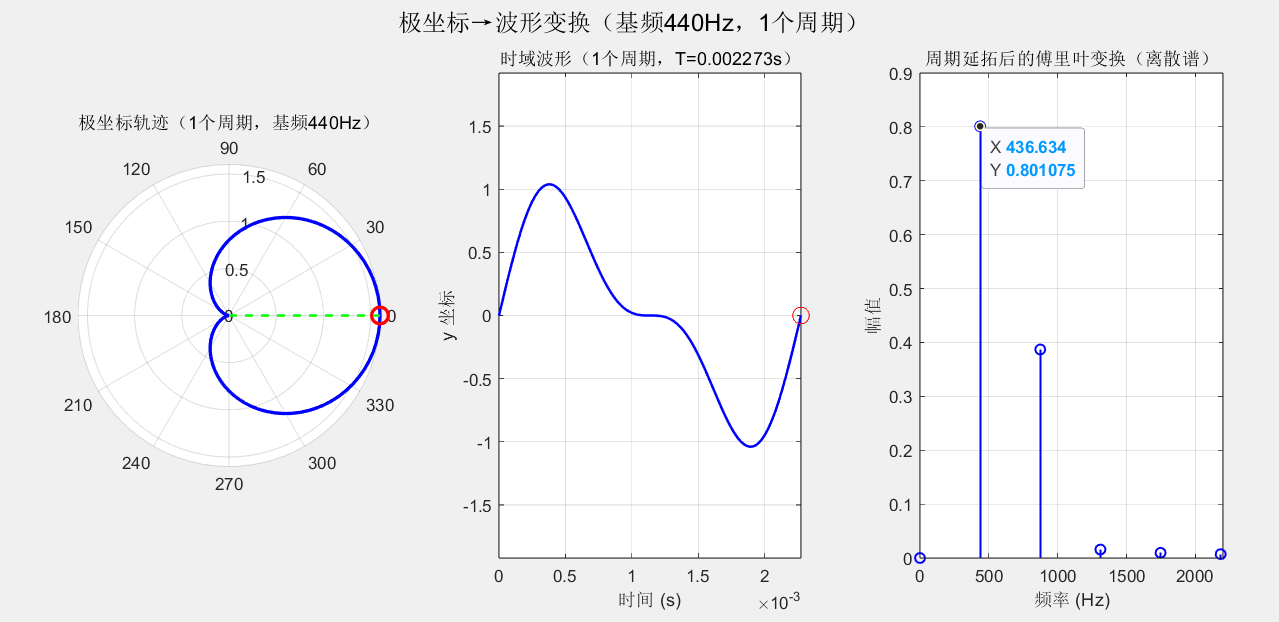
接下来我遇到了一个bug
进行到双纽线这里，发现生成的波形有一大段是不连续的------
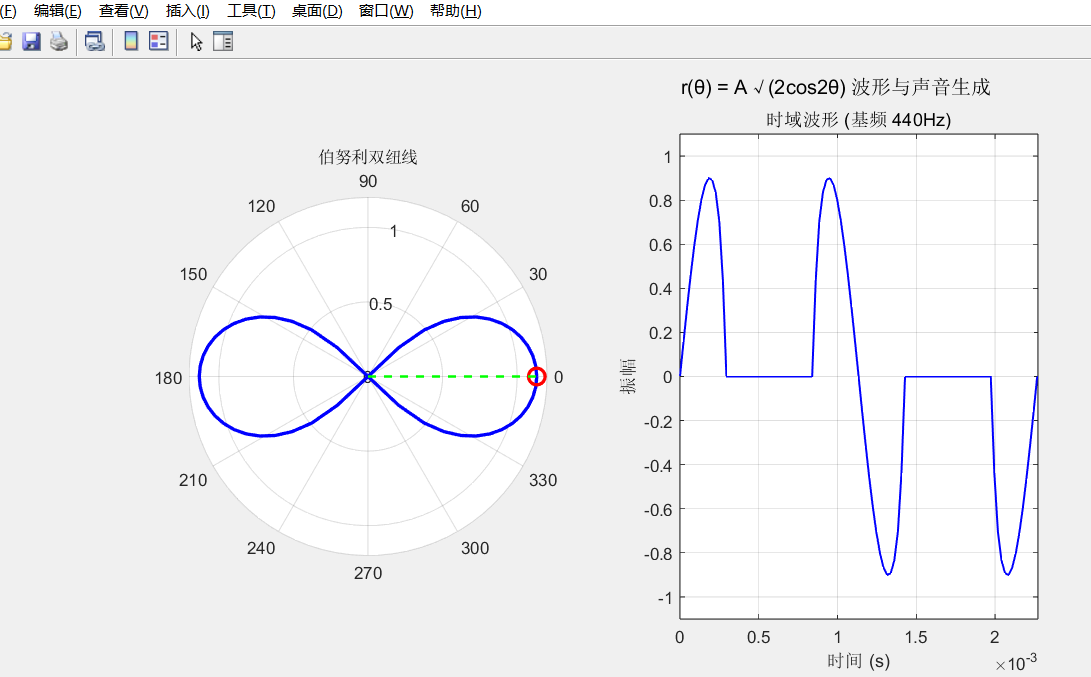
看了函数的定义后，发现不连续的地方是因为对应的相位部分，双纽线的极径r是虚数，在振幅转换之后就一直在0处。
从数学意义上讲，若要通过极坐标函数生成连续光滑的波形，极坐标函数需满足以下条件：
- 极径函数连续性：极径函数在定义域范围内必须是连续的，不能出现间断点。
- 极径函数可导性：极径函数在定义域范围内需要是可导的，确保波形在时域上光滑无突变。
- 极径函数非负性：极径函数在定义域范围内需非负，避免出现虚数或负值导致波形失真。
- 周期性：极径函数需具有周期性，以保证生成的波形在时域上是周期性的，从而使得频谱分析有意义。
- 频率成分可控性：极径函数的频率成分需可控，以确保生成的波形在频域上具有特定的频率特性，如单一频率、多个频率的组合等。
当然，声音的波形并不非要光滑连续，毕竟最终存储编码都是离散的，像锯齿波、方波这些，也有很独特的音响效果。
最终代码如下：
（代码运行会播放声音，注意调节音量！）
Matlab
clear; clc; close all;
%%
% 核心参数设置
f0 = 440; % 基频440Hz（A4标准音）
duration = 1; % 声音时长1秒
fs = 44100; % 采样频率
T = 1/f0; % 周期
N_per_period = ceil(fs*T); % 一个周期的采样点数
N_total = fs*duration; % 总采样点数
A = 0.8; % 振幅系数
% 定义30种不同的极坐标函数
polar_functions = [
% 基础曲线
struct('name', '圆形 (Circle)', 'expr', 'r(θ) = A', 'func', @(theta, A) A*ones(size(theta)));
struct('name', '心形线 (Cardioid)', 'expr', 'r(θ) = A(1 + cosθ)', 'func', @(theta, A) A*(1 + cos(theta)));
struct('name', '3瓣玫瑰线', 'expr', 'r(θ) = A*cos(3θ)', 'func', @(theta, A) A*cos(3*theta));
struct('name', '4瓣玫瑰线', 'expr', 'r(θ) = A*cos(2θ)', 'func', @(theta, A) A*cos(2*theta));
struct('name', '5瓣玫瑰线', 'expr', 'r(θ) = A*cos(5θ)', 'func', @(theta, A) A*cos(5*theta));
struct('name', '6瓣玫瑰线', 'expr', 'r(θ) = A*cos(3θ)', 'func', @(theta, A) A*cos(3*theta));
struct('name', '7瓣玫瑰线', 'expr', 'r(θ) = A*cos(7θ)', 'func', @(theta, A) A*cos(7*theta));
struct('name', '8瓣玫瑰线', 'expr', 'r(θ) = A*cos(4θ)', 'func', @(theta, A) A*cos(4*theta));
struct('name', '9瓣玫瑰线', 'expr', 'r(θ) = A*cos(9θ)', 'func', @(theta, A) A*cos(9*theta));
struct('name', '10瓣玫瑰线', 'expr', 'r(θ) = A*cos(5θ)', 'func', @(theta, A) A*cos(5*theta));
% 螺线族
struct('name', '阿基米德螺线', 'expr', 'r(θ) = Aθ', 'func', @(theta, A) A*theta);
struct('name', '对数螺线', 'expr', 'r(θ) = A·e^{(kθ)}', 'func', @(theta, A) A*exp(0.2*theta));
struct('name', '费马螺线', 'expr', 'r²(θ) = A²θ', 'func', @(theta, A) A*sqrt(theta));
struct('name', '双曲螺线', 'expr', 'r(θ) = A/θ', 'func', @(theta, A) A./(theta + 0.5));
% 其他曲线
struct('name', '伯努利双纽线', 'expr', 'r(θ) = A√{2cos2θ}', 'func', @(theta, A) A*sqrt(2*cos(2*theta)));
struct('name', '卡西尼卵形线', 'expr', 'r²(θ) = A²cos2θ + B²', 'func', @(theta, A) sqrt(A^2*cos(2*theta) + 0.5^2));
struct('name', '椭圆', 'expr', 'r(θ) = A/(1 + ecosθ)', 'func', @(theta, A) A./(1 + 0.5*cos(theta)));
struct('name', '正弦曲线', 'expr', 'r(θ) = A + B·sin(nθ)', 'func', @(theta, A) A + 0.4*sin(3*theta));
struct('name', '余弦曲线', 'expr', 'r(θ) = A + B·cos(nθ)', 'func', @(theta, A) A + 0.4*cos(3*theta));
struct('name', '正切曲线', 'expr', 'r(θ) = A·tan(θ)', 'func', @(theta, A) A*tan(theta/2));
% 新增曲线
struct('name', '指数曲线', 'expr', 'r(θ) = A·e^{(kθ)}', 'func', @(theta, A) A*exp(0.1*theta));
struct('name', '圆内螺线', 'expr', 'r(θ) = A·cos(nθ) + B', 'func', @(theta, A) A*cos(5*theta) + 0.5);
struct('name', '圆外螺线', 'expr', 'r(θ) = A·cos(nθ)-B', 'func', @(theta, A) A*cos(5*theta)-0.5);
struct('name', '肾形线', 'expr', 'r(θ) = A(1 + cosθ)', 'func', @(theta, A) A*(1 + cos(theta)));
struct('name', '蜗牛线', 'expr', 'r(θ) = A(1 + cosθ) + B', 'func', @(theta, A) A*(1 + cos(theta)) + 0.3);
struct('name', '双叶线', 'expr', 'r(θ) = A·sin(nθ/2)', 'func', @(theta, A) A*sin(5*theta/2));
struct('name', '三叶线', 'expr', 'r(θ) = A·sin(nθ/3)', 'func', @(theta, A) A*sin(5*theta/3));
struct('name', '四叶线', 'expr', 'r(θ) = A·sin(nθ/4)', 'func', @(theta, A) A*sin(5*theta/4));
struct('name', '五叶线', 'expr', 'r(θ) = A·sin(nθ/5)', 'func', @(theta, A) A*sin(5*theta/5));
struct('name', '六叶线', 'expr', 'r(θ) = A·sin(nθ/6)', 'func', @(theta, A) A*sin(5*theta/6));
struct('name', '七叶线', 'expr', 'r(θ) = A·sin(nθ/7)', 'func', @(theta, A) A*sin(5*theta/7));
struct('name', '八叶线', 'expr', 'r(θ) = A·sin(nθ/8)', 'func', @(theta, A) A*sin(5*theta/8));
struct('name', '九叶线', 'expr', 'r(θ) = A·sin(nθ/9)', 'func', @(theta, A) A*sin(5*theta/9));
struct('name', '十叶线', 'expr', 'r(θ) = A·sin(nθ/10)', 'func', @(theta, A) A*sin(5*theta/10));
];
% 生成一个周期的时间和角度向量
t_one_period = linspace(0, T, N_per_period);
theta_one_period = 2*pi*(t_one_period/T);
% 循环处理每个极坐标函数
for i = 1:length(polar_functions)
func = polar_functions(i);
% 生成一个周期的波形
r_one_period = func.func(theta_one_period, A);
% 处理可能出现的复数或负值（对于某些极坐标函数）
r_one_period = abs(real(r_one_period));
y_one_period = r_one_period .* sin(theta_one_period);
% 扩展为1秒的波形（复制粘贴周期波形）
y = repmat(y_one_period, 1, ceil(N_total/N_per_period));
y = y(1:N_total); % 确保正好1秒
t_full = linspace(0, duration, N_total); % 完整时间向量
% 归一化处理（避免声音失真）
y_normalized = y / max(abs(y)) * 0.9;
% 保存为WAV文件
filename = sprintf('polar_waveform_%d.wav', i);
audiowrite(filename, y_normalized, fs);
fprintf('声音已保存为: %s\n', fullfile(pwd, filename));
% 绘制极坐标轨迹
figure('Position',[100 100 1400 500]);
% 1. 极坐标轨迹
subplot(1,3,1);
polarplot(theta_one_period, r_one_period, 'b-', 'LineWidth',2);
hold on;
polarplot(theta_one_period(end), r_one_period(end), 'ro', 'MarkerSize',10, 'LineWidth',2);
polarplot([theta_one_period(end), theta_one_period(end)], [0, r_one_period(end)], 'g--', 'LineWidth',1.5);
title(func.name, 'FontSize',10);
hold off;
% 2. 一个周期的时域波形
subplot(1,3,2);
plot(t_full, y_normalized, 'b-', 'LineWidth',1.2);
xlabel('时间 (s)');
ylabel('振幅');
title(['时域波形 (基频 ' num2str(f0) 'Hz)']);
xlim([0 T]);
ylim([-1.1 1.1]);
grid on;
% 3. 周期延拓后的傅里叶变换
subplot(1,3,3);
Y = fft(y_one_period - mean(y_one_period)); % 对一个周期做FFT
f = (0:N_per_period-1)*(fs/N_per_period); % 频率轴
amp = abs(Y)/N_per_period*2; % 幅值归一化
max_harmonic = 5;
f_range = f(f <= max_harmonic*f0);
amp_range = amp(f <= max_harmonic*f0);
stem(f_range, amp_range, 'b-', 'MarkerSize',6, 'LineWidth',1.2);
xlabel('频率 (Hz)');
ylabel('幅值');
title('周期延拓后的频谱');
xlim([0 max_harmonic*f0]);
grid on;
sgtitle([func.expr ' 波形与声音生成'], 'FontSize',12);
fprintf('正在显示 %s 的图形...\n', func.name);
pause(2); % 显示图形2秒
% 播放声音
sound(y_normalized, fs);
fprintf('正在播放 %s 的声音...\n', func.name);
pause(duration + 0.5); % 等待声音播放完毕，加0.5秒缓冲
end
fprintf('所有极坐标函数的波形和声音已生成完毕。\n');最后生成的3-10叶线（AI这么叫的，这里只是一个代号，与数学上的定义并不相符和实际上曲线的叶数，笔者只是在研究音乐，所以就不较真了）因为周期不足，因此只绘制了一个周期的部分，如果周期绘制充足，按理来说是频率是会降低的，所以我又请AI帮忙写代码把这些线的频率调高，完整绘制对应到440Hz的频率内。
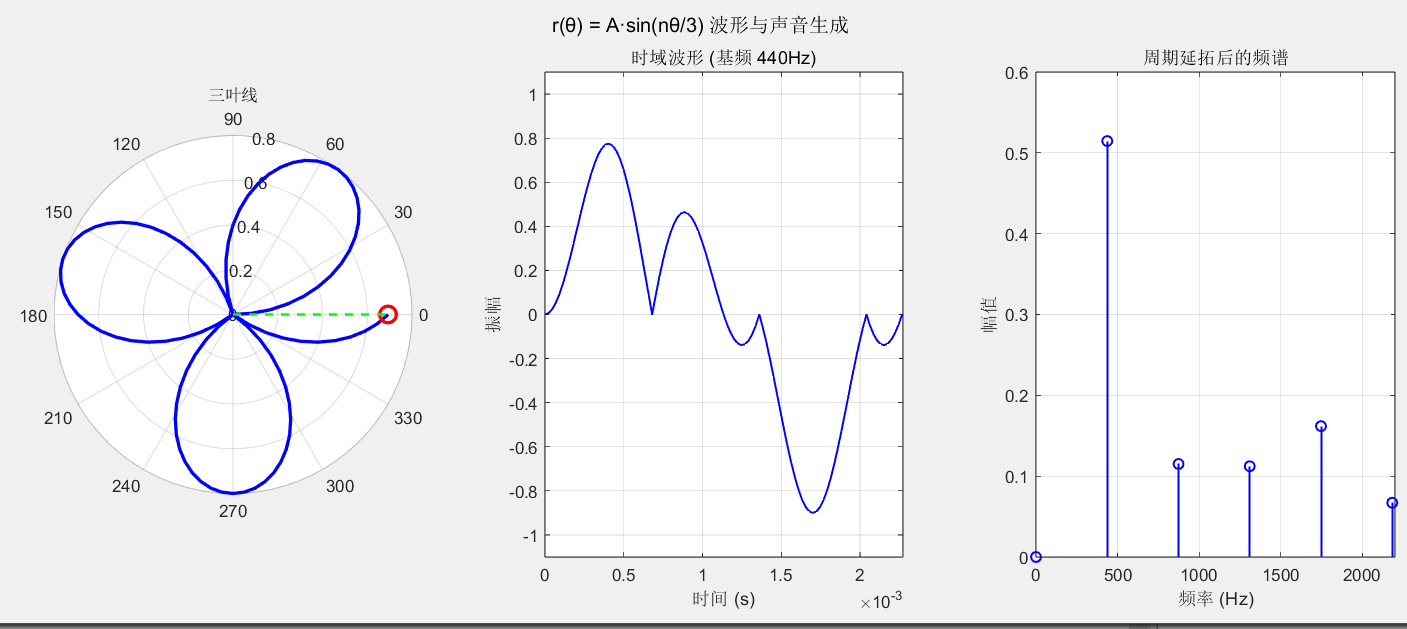未绘制完整的曲线
代码如下：
Matlab
% 核心参数设置（确保基频440Hz）
f0 = 440; % 基频440Hz
duration = 1; % 声音时长1秒
fs = 44100; % 采样频率
T = 1/f0; % 时域周期（1/440秒）
N_per_period = ceil(fs*T); % 一个时域周期的采样点数（声音采样精度）
high_res_factor = 30; % 极坐标绘图分辨率提升倍数（30倍超采样）
A = 0.8; % 振幅系数
% 定义3-10叶线的极坐标函数（叶数n=3到10）
polar_functions = [
struct('name', '三叶线', 'n', 3, 'expr', 'r(θ) = A·sin(nθ/3)', 'func', @(theta, A, n) A*sin(n*theta/n));
struct('name', '四叶线', 'n', 4, 'expr', 'r(θ) = A·sin(nθ/4)', 'func', @(theta, A, n) A*sin(n*theta/n));
struct('name', '五叶线', 'n', 5, 'expr', 'r(θ) = A·sin(nθ/5)', 'func', @(theta, A, n) A*sin(n*theta/n));
struct('name', '六叶线', 'n', 6, 'expr', 'r(θ) = A·sin(nθ/6)', 'func', @(theta, A, n) A*sin(n*theta/n));
struct('name', '七叶线', 'n', 7, 'expr', 'r(θ) = A·sin(nθ/7)', 'func', @(theta, A, n) A*sin(n*theta/n));
struct('name', '八叶线', 'n', 8, 'expr', 'r(θ) = A·sin(nθ/8)', 'func', @(theta, A, n) A*sin(n*theta/n));
struct('name', '九叶线', 'n', 9, 'expr', 'r(θ) = A·sin(nθ/9)', 'func', @(theta, A, n) A*sin(n*theta/n));
struct('name', '十叶线', 'n', 10, 'expr', 'r(θ) = A·sin(nθ/10)', 'func', @(theta, A, n) A*sin(n*theta/n));
];
% 生成时域周期内的时间向量（声音采样精度）
t_one_period = linspace(0, T, N_per_period);
% 循环处理每个叶线函数
for i = 1:length(polar_functions)
func = polar_functions(i);
n = func.n; % 叶数
% 1. 声音生成用（保持基频精度）
theta_sound = linspace(0, 2*pi*n, N_per_period);
r_sound = func.func(theta_sound, A, n);
r_sound = abs(real(r_sound));
y_one_period = r_sound .* sin(theta_sound); % 声音波形
% 扩展为1秒波形
y = repmat(y_one_period, 1, ceil(fs*duration/N_per_period));
y = y(1:fs*duration); % 确保正好1秒
y_normalized = y / max(abs(y)) * 0.9; % 归一化
% 2. 高分辨率绘图用（提升视觉精细度）
N_high_res = N_per_period * high_res_factor; % 高分辨率点数
theta_plot = linspace(0, 2*pi*n, N_high_res); % 极角超采样
r_plot = func.func(theta_plot, A, n);
r_plot = abs(real(r_plot)); % 处理复数和负值
% 保存为WAV文件
filename = sprintf('%d叶线_sound.wav', n);
audiowrite(filename, y_normalized, fs);
fprintf('%d叶线声音已保存为: %s\n', n, fullfile(pwd, filename));
% 绘制高分辨率图形
figure('Position',[100 100 1400 500]);
% 1. 极坐标轨迹（高分辨率显示）
subplot(1,3,1);
% 通过增加采样点和细化线条来提高精度
polarplot(theta_plot, r_plot, 'b-', 'LineWidth',1.2);
hold on;
polarplot(theta_plot(end), r_plot(end), 'ro', 'MarkerSize',8);
polarplot([theta_plot(end), theta_plot(end)], [0, r_plot(end)], 'g--', 'LineWidth',1);
title([func.name ' (极坐标' num2str(n) '个周期)'], 'FontSize',10);
% 优化极坐标刻度显示
ax = gca;
ax.ThetaTick = 0:30:330; % 显示0°,30°,60°,...330°刻度
ax.RTick = linspace(0, max(r_plot), 5); % 合理设置径向刻度
hold off;
% 2. 时域波形（声音采样精度）
subplot(1,3,2);
plot(t_one_period, y_one_period, 'b-', 'LineWidth',1.2);
xlabel('时间 (s)');
ylabel('振幅');
title([func.name ' 时域波形 (基频' num2str(f0) 'Hz)']);
xlim([0 T]);
ylim([-1.1 1.1]);
grid on;
% 3. 频谱分析
subplot(1,3,3);
Y = fft(y_one_period - mean(y_one_period));
f = (0:N_per_period-1)*(fs/N_per_period);
amp = abs(Y)/N_per_period*2;
max_harmonic = 5;
f_range = f(f <= max_harmonic*f0);
amp_range = amp(f <= max_harmonic*f0);
stem(f_range, amp_range, 'b-', 'MarkerSize',6);
xlabel('频率 (Hz)');
ylabel('幅值');
title('周期延拓后的频谱');
xlim([0 max_harmonic*f0]);
grid on;
sgtitle([func.expr ' 高分辨率波形与声音生成'], 'FontSize',12);
pause(2); % 显示图形2秒
% 播放声音
sound(y_normalized, fs);
fprintf('正在播放%d叶线声音...\n', n);
pause(duration + 0.5); % 等待声音播放完毕
end
fprintf('所有叶线的高分辨率波形和声音已生成完毕。\n');绘制完整后，我才发现我的设想是错误的。
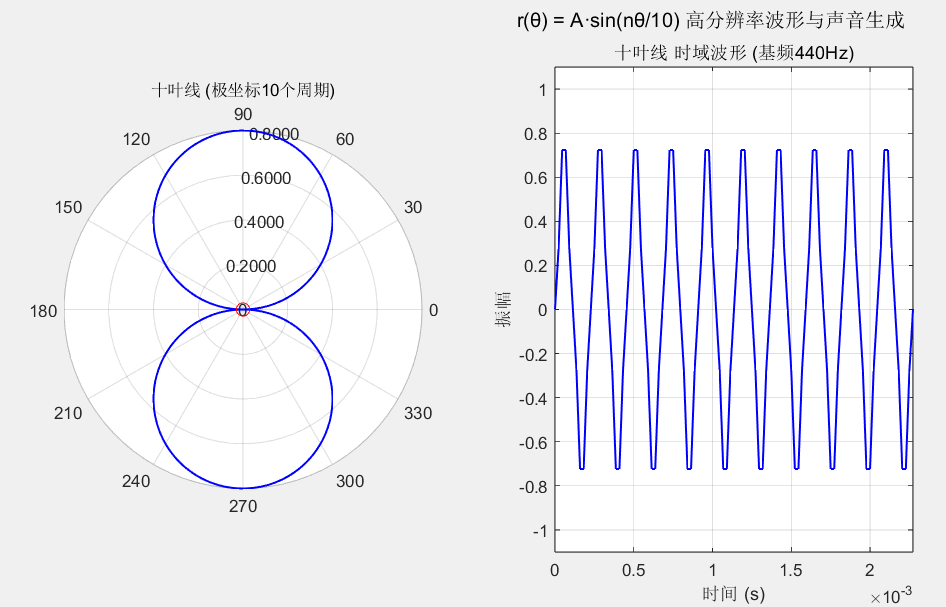
因为这样一来，所有的曲线都会变成一个几乎重叠的两瓣玫瑰线。
所以从理论上讲，生成的音频的理想情况是按照440Hz的n倍往上增长。
运行代码，聆听声音，我发现了一个很有趣的现象，虽然高频很明显地在往上增长，但是低频（尤其是440Hz的基频的听感始终存在）
使用AU打开刚刚保存的波形，可以发现，哪怕是频率最高的所谓十叶线的波形，画红框的部分也是有基频存在的，其他的440Hz的倍频也是存在的。
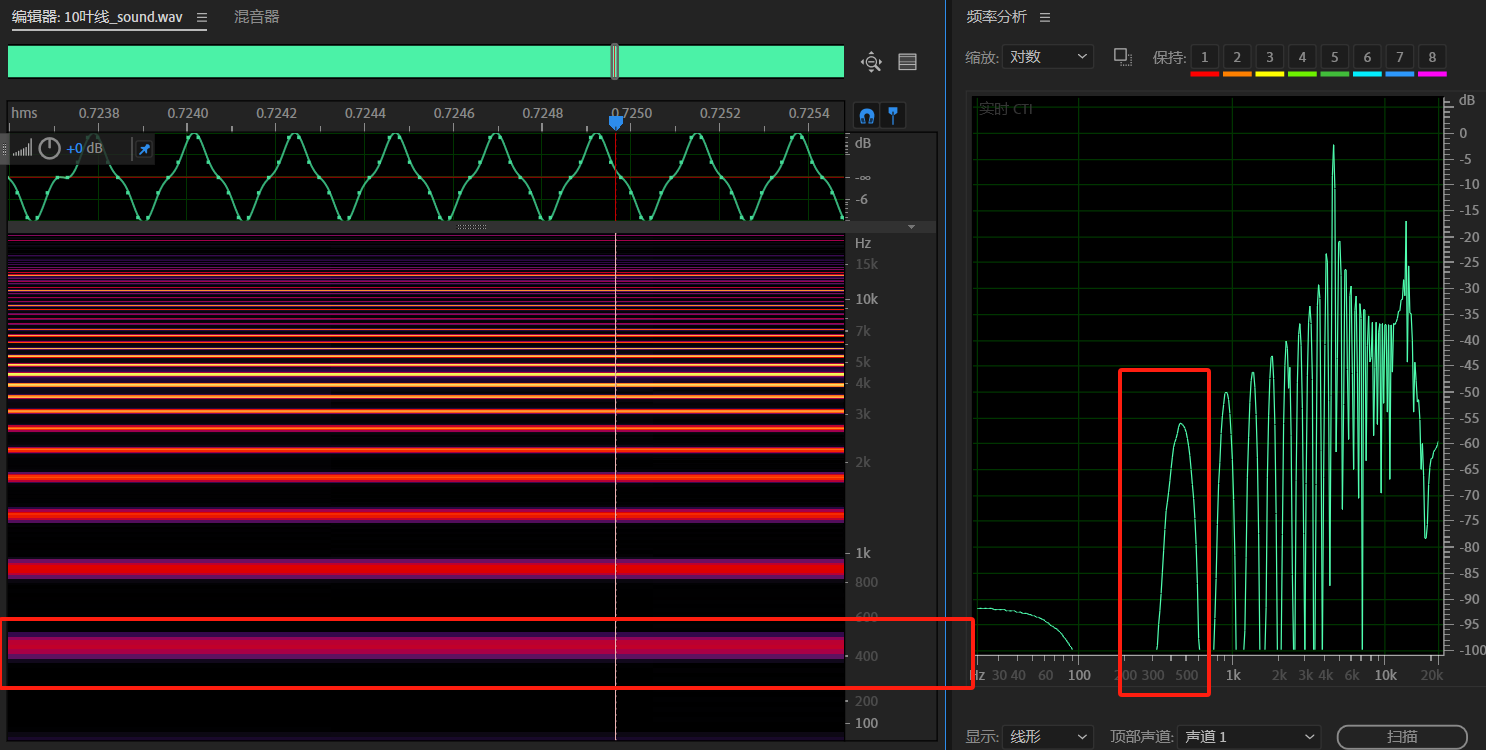
这是为什么呢？
笔者的解释是，因为我们在代码中进行的是仿真采样，并不是根据数学公式推导，所以对于所谓"n叶线"，是一个重复的波形的n次绘图，采样后带来的误差在每个小周期内都是不一样的，只有n个周期（对应440Hz的基频）是完整重复的。总体上，这就导致了只有440Hz才是最终的基频。
解释的不是很明白，请AI帮忙------
它这样说：
要理解为何十叶线等波形中始终存在 440Hz 基频及其倍频，核心在于信号的时间周期性由整体重复周期决定，而非局部波动次数。你的观察本质上涉及 "空间周期性" 与 "时间周期性" 的区别、信号基频的定义，以及仿真中波形生成逻辑的影响，具体可以从这三个层面拆解：
一、先明确：基频的本质是 "信号整体重复的周期"
基频（f₀） 的物理意义是信号完成一次完整重复的时间周期（T）的倒数，即 f₀=1/T。无论波形内部有多少局部波动（比如 n 叶线的 n 个 "叶"），只要整体波形每 T 时间重复一次，基频就只能是 1/T。
在你的仿真中，若设定 "绘制 n 叶线的总时间为 T=1/440 秒"（即 440Hz 对应的周期），那么整个 n 叶线的波形会在每 1/440 秒后完全重复一次 ------ 比如十叶线的 10 个 "叶" 会在 1/440 秒内画完，下一个 1/440 秒又会一模一样地画一次 10 个 "叶"。此时，信号的整体周期 T=1/440 秒，基频自然是 440Hz，与 n 的大小无关。
二、n 叶线的 "n 个叶" 是 "局部波动"，而非 "独立周期"
你提到 "n 叶线是重复的波形的 n 次绘图"，这里的 "n 次绘图" 本质是一个基频周期内的 n 次局部波动，而非 n 个独立的小周期。
举个例子：假设 n=10（十叶线），在 T=1/440 秒内，波形会有 10 个起伏（10 个叶），但这 10 个起伏并不满足 "周期性"------ 即第 1 个叶的波形和第 2 个叶的波形可能相似但不会完全重复（比如极坐标中 θ 的起始位置不同），且不会在 T'=T/10=1/(440×10) 秒后独立重复。真正重复的是 "10 个叶的完整组合"，每 T=1/440 秒重复一次。
因此，这 10 个叶只是基频周期内的 "细节波动"，不会产生 10×440Hz 的新基频，反而会因为这些波动是基频周期内的 "谐波成分"，从而产生 440Hz 的倍频（如 880Hz、1320Hz 等）。
三、仿真采样的误差不是主因，核心是 "波形生成逻辑"
你提到 "采样误差导致每个小周期不同"，但这并非基频存在的关键原因。即使采样完全理想（无误差），只要波形的整体重复周期是 T=1/440 秒，基频就必然是 440Hz。
原因在于你的仿真逻辑：是 "在一个 440Hz 周期内画 n 个叶"，而非 "让每个叶对应一个独立周期"。比如，若想让十叶线的基频是 4400Hz（10×440），需要设定 "每个叶的绘制时间为 T'=1/4400 秒，且单个叶的波形会在 T' 内重复"，但此时整体波形的周期就变成了 T'，而非原来的 T=1/440 秒 ------ 显然这与你的仿真设定不符。
总结：基频由 "整体重复周期" 说了算
十叶线等波形中始终存在 440Hz 基频，根本原因是整个波形的重复周期被设定为 440Hz 对应的周期（1/440 秒）。n 叶线的 "n 个叶" 只是这个周期内的局部细节，不会改变整体的重复规律。无论是仿真采样还是数学推导，只要信号的整体周期不变，基频就不会变；而局部波动带来的倍频（440Hz 的 2 倍、3 倍等），恰恰是这些细节在基频周期内的 "谐波表现"。
简单说：n 叶线的 "n" 决定了一个基频周期内有多少个 "褶皱"，但 "褶皱数量" 不影响 "多久皱一次"------ 后者才是基频的本质。
我觉得它虽然说得对，但是并没有理解问题的关键，尤其是第三点。诸位怎么理解，见仁见智吧。
仔细看波形，你可以发现，实际上带来基频的，是每n个周期重复一次的这一小段波形
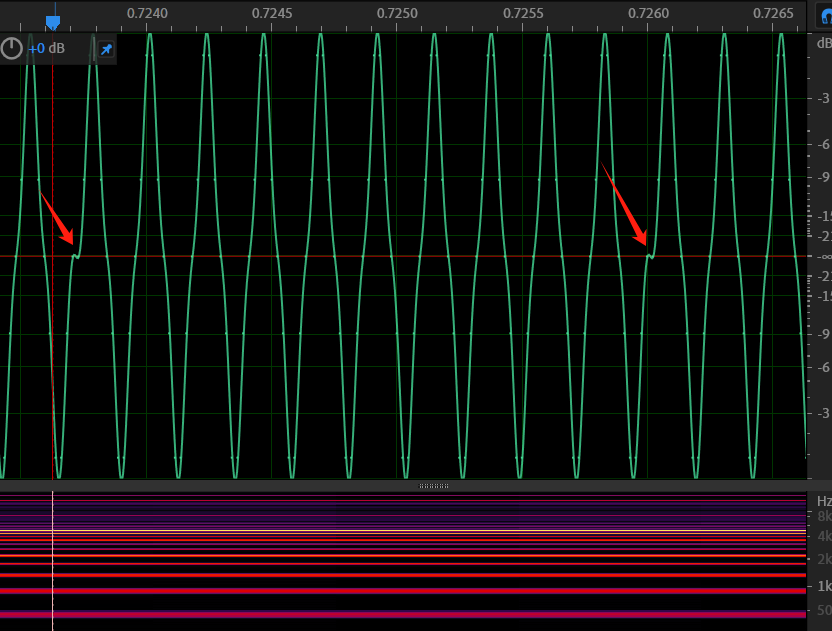"十叶线"------每十个一组，衔接的部分很明显 
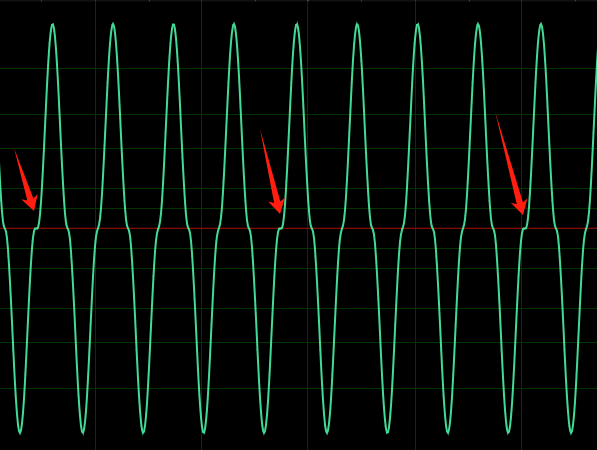"四叶线"，不是很明显，但是也能看出来
如果绘制与采样完全没有误差，这些波形完美地首尾相接，那么基频就是一个小周期对应的频率，不会有更低的440Hz出现。
未完待续~