【本章学习建议】
根据考试大纲,本章主要考查系统架构设计师单选题 ,预计考2分左右。主要是运筹学的计算问题,范围广、难度大,超纲题较多,不用深究。

1 6 .1 线性规划
线性规划 是研究在有限的资源条件下,如果有效地使用这些资源达到预定目标的数学方法,即在一组约束条件下求目标函数的极值(极大值或极小值)。
线性规划问题的数学模型通常由线性目标函数、线性约束条件、变量非负条件组成(实际问题中的变量一般都是非负的)。
线性规划问题就是面向实际应用,求解一组非负变量,使其满足给定的一组线性约束条件,并使某个线性目标函数达到极值。满足这些约束条件的非负变量组的集合称为可行解域 。可行解域中使目标函数达到极值的解 称为最优解。
线性规划问题的最优解:无可行解、无最优解、一个最优解或无穷多个最优解。
快速解题步骤(求交点) :①根据题目条件列出不等式或不等式组;②将不等关系特殊化为等式,两两等式联立求交点 ;③若交点值满足所有约束条件,直接代入目标函数求得极值即可;若交点值不满足约束条件,继续计算其他两两等式。(若交点值不满足实际情况,取附近值即可,如小数个人)。
1 6 .2 蒙特卡罗方法
蒙特卡罗 (Monte Carlo)方法 由冯・诺依曼、乌拉姆等人发明,因赌场而得名,是一类基于概率的方法的统称。
1. 工作原理
使用随机数来解决计算问题。不断抽样,逐渐逼近,采样越多,越近似最优解 。例如民意调查,π的计算。
2. 应用案例
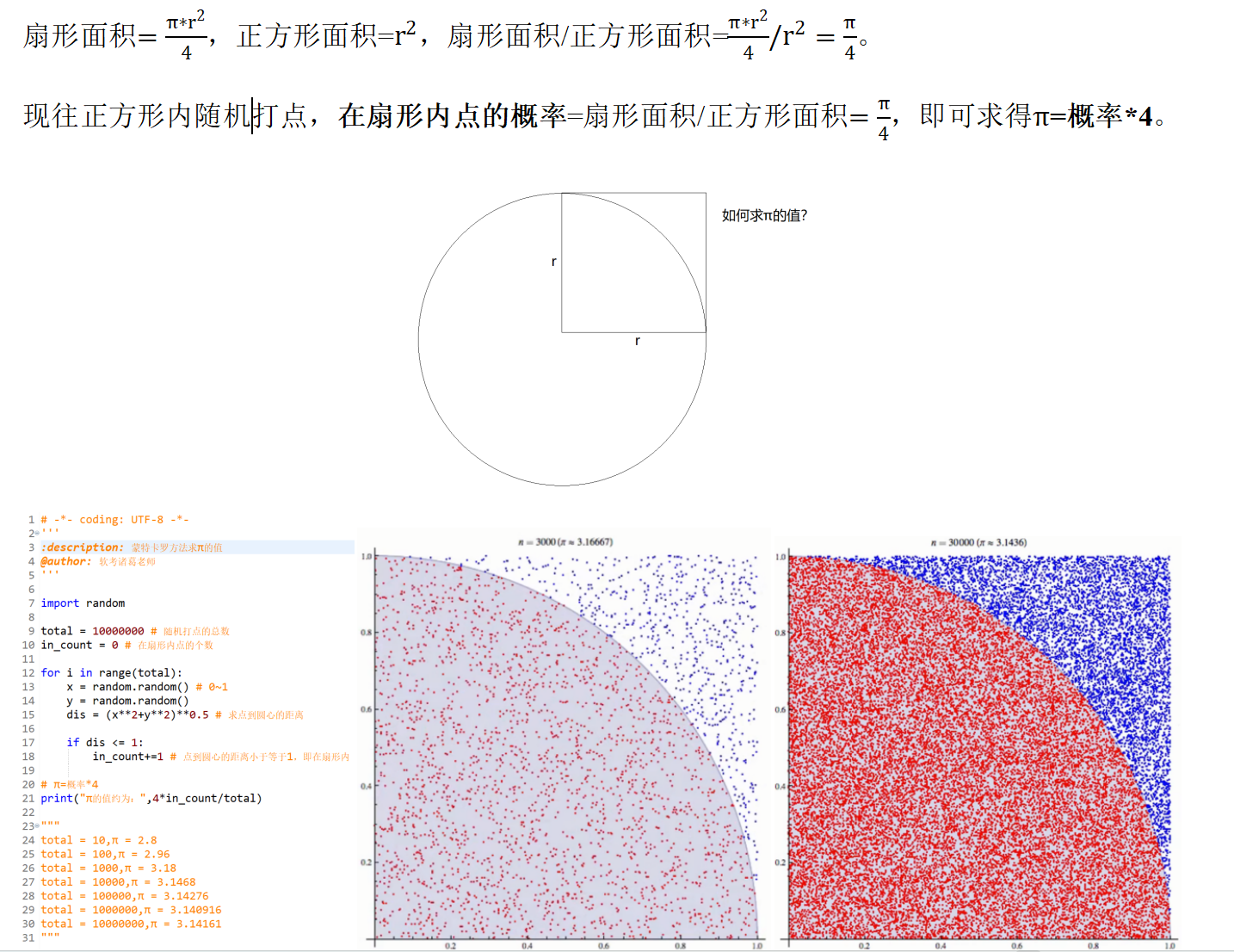
16 . 3 数学建模
数学建模是对现实世界的一种近似的、简化的、易于求解的抽象描述。通过抽象和简化,建立能近似刻画并解决实际问题的模型。
1. 数学建模过程
(1)模型准备:了解问题的实际背景,明确其实际意义,掌握对象的各种信息。用数学语言来描述问题。
(2)模型假设:根据实际对象的特征和建模的目的,对问题进行必要的简化,并用精确的语言提出一些恰当的假设。
(3)模型建立:在假设的基础上,利用适当的数字工具来刻画各变量之间的数学关系,建立相应的数学结构。只要能够把问题描述清楚,尽量使用简单的数字工具。
(4)模型求解:利用获取的数据资料,对模型的所有参数做出计算(估计)。
(5)模型分析:对所得的结果进行数学上的分析。如敏感性分析:测试模型对参数变化的敏感性,对计算结果进行检验,分析计算结果对参数变化的反应程度。
(6)模型检验:将模型分析结果与实际情形进行比较,以此来验证模型的准确性、合理性和适用性。如果模型与实际较吻合,则要对计算结果给出其实际含义,并进行解释。如果模型与实际吻合较差,则应该修改假设,再次重复建摸过程。
(7)模型应用:将模型应用于新的数据集或场景中,以进行预测或决策支持。应用方式因问题的性质和建模的目的而异。
2. 数学建模方法
·直接分析法:根据对问题直接的内在的认识,直接构造出模型。
·类比法:根据之前类似的模型构造出一个新的模型。
·数据分析法:通过实验获得与问题相关的大量数据,用统计分析的方法来进行建模。
·构想法:对将来可能发生的情况给出逻辑上合理的方法和描述,而后用现有的方法来建模,不断地完善。
3. 数学建模原则
·需要在简单性和准确性之间求得平衡。
·对同一问题可以建立多种数学模型。数学模型常带有多个参数,而参数会随环境因素而变化。选用哪个模型,或选择什么样的参数,这需要反复多次试验,根据求解失败的教训或用户的反馈意见逐步对模型进行修正或改进,逐步完善模型。
16 . 4 动态规划
动态规划 的基本思想是将待求解问题分解成若干个子问题,先求解子问题,然后从这些子问题的解得到原问题的解,以解决最优化问题的算法策略。
16 . 5 决策论
决策论是研究为了达到预期目的,从多个可供选择的方案中如何选取最好或满意方案的学科。
决策的六个要素:
决策者、可供选择的方案(包括行动、策略)、衡量选择方案的准则(目的、目标、正确性等)、事件(被决策的对象)、每一事件的发生将会产生的某种结果、决策者的价值观。
决策论的分类:
·确定型决策:决策环境是确定的,结果也是确定的。
·风险决策:决策环境是不确定的,但是结果发生的概率是一致的。
·不确定型决策:决策环境不确定,且结果也不确定,完全凭主观意识来决定。
不确定型决策的五种方案:
·乐观主义准则,大中取大max(max),先取每个方案最大的收益,再取所有最大收益中最大的那个;
·悲观主义准则,小中取大max(min),先取每个方案最小的收益,再取所有最小收益中最大的那个;
·折中主义准则,设定折中系数a,用每个方案的最大收益*a+最小收益*(1-a),选择每个方案中计算结果最大的那个,可知,a=1时为乐观主义,a=0时为悲观主义;
·等可能性准则,设定每个可能结果的发生都是等可能的,这样就知道每个结果发生的概率,即将不确定型的问题转换为了风险决策问题;
·后悔值准则,最小最大后悔值min(max),计算各个方案在每种情况下的后悔值(后悔值=各个方案在该情况下的最大收益-该情况下该方案的收益),找出各个方案的最大后悔值,再从这些最大后悔值中选出最小值,这个最小值对应的策略就是选择的策略。