【MATLAB第116期】基于MATLAB的NBRO-XGBoost的SHAP可解释回归模型(敏感性分析方法)
引言
该文章实现了一个可解释的回归模型,使用NBRO-XGBoost(方法可以替换,但是需要有一定的编程基础)来预测特征输出。该模型利用七个变量参数作为输入特征进行训练。为了提高可解释性,应用了SHapley Additive exPlanations(SHAP),去深入了解每个参数对模型预测的贡献。
第112期用了BP神经网络作为代理模型, xgboost难度在于其环境配置,其次代码的更改,以及最重要的是计算速度,目前已解决上述问题。
一、NBRO-XGBoost模型训练
matlab
% 清空环境变量
warning off % 关闭报警信息
close all % 关闭开启的图窗
clear % 清空变量
clc % 清空命令行
%% 导入数据
res = xlsread('数据集.xlsx');
%% 数据分析
num_size = 0.8; % 训练集占数据集比例
outdim = 1; % 最后1列为输出
num_samples = size(res, 1); % 样本个数
res = res(randperm(num_samples), :); % 打乱数据集(不希望打乱时,注释该行)
num_train_s = round(num_size * num_samples); % 训练集样本个数
f_ = size(res, 2) - outdim; % 输入特征维度
id=1; % 输出第几个因变量()
%% 划分训练集和测试集
P_train = res(1: num_train_s, 1: f_)';
T_train = res(1: num_train_s, f_ +id)';
%T_train=mean(T_train0);
M = size(P_train, 2);
P_test = res(num_train_s + 1: end, 1: f_)';
T_test = res(num_train_s + 1: end, f_ + id)';
%T_test=mean(T_test0);
N = size(P_test, 2);
%% 数据归一化
[p_train, ps_input] = mapminmax(P_train, 0, 1);%将训练集和测试集的数据调整到0到1之间
p_test = mapminmax('apply', P_test, ps_input);
[t_train, ps_output] = mapminmax(T_train, 0, 1);% 对测试集数据做归一化
t_test = mapminmax('apply', T_test, ps_output);
%% 数据转置 为适应模型的建立
p_train = p_train'; p_test = p_test';
t_train = t_train'; t_test = t_test';
%% 参数设置
fun = @getObjValue; % 目标函数
dim = 3; % 优化参数个数
lb = [10, 10, 0.01]; % 优化参数目标下限(最大迭代次数,深度,学习率)
ub = [200, 20, 1]; % 优化参数目标上限(最大迭代次数,深度,学习率)
SearchAgents_no = 10; % 种群数量6
Max_iteration = 10; % 最大迭代次数20
params.objective = 'reg:linear'; % 回归函数
%% 优化算法
[Best_score ,Best_pos, curve] = NRBO(SearchAgents_no, Max_iteration, lb, ub, dim, fun);
%% 获取最优参数
num_trees = round(Best_pos(1, 1)); % 迭代次数
params.max_depth = round(Best_pos(1, 2)); % 树的深度
params.eta = Best_pos(1, 3); % 学习率
%% 建立模型
for j = 1 : size(t_train,2)
%% 建立模型
model(j) = xgboost_train(p_train, t_train(:,j), params, num_trees);
%% 模型预测
t_sim1(:,j) = xgboost_test(p_train, model(j));
t_sim2(:,j) = xgboost_test(p_test , model(j));
end
%% 数据反归一化
T_sim1 = mapminmax('reverse', t_sim1', ps_output);
T_sim2 = mapminmax('reverse', t_sim2', ps_output);
figure
plot(1 : length(curve), curve, 'LineWidth', 1.5);
title('NRBO-XGboost', 'FontSize', 10);
xlabel('迭代次数', 'FontSize', 10);
ylabel('适应度值', 'FontSize', 10);
grid on
%% 评价指标
%% 绘图
for i = 1 : 1
figure
%% 均方根误差
error1 = sqrt(sum((T_sim1(i, :) - T_train(i, :)).^2) ./ M);
error2 = sqrt(sum((T_sim2(i, :) - T_test (i, :)).^2) ./ N);
subplot(2, 1, 1)
plot(1: M, T_train(i, :), 'r-', 1: M, T_sim1(i, :), 'b-', 'LineWidth', 1)
legend('真实值', 'NRBO-XGboost预测值')
xlabel('预测样本')
ylabel('预测结果')
string = {'训练集预测结果对比'; ['RMSE=' num2str(error1)]};
title(string)
xlim([1, M])
grid
subplot(2, 1, 2)
plot(1: N, T_test(i, :), 'r-', 1: N, T_sim2(i, :), 'b-o', 'LineWidth', 1)
legend('真实值', 'NRBO-XGboost预测值')
xlabel('预测样本')
ylabel('预测结果')
string = {'测试集预测结果对比'; ['RMSE=' num2str(error2)]};
title(string)
xlim([1, N])
grid
%% 相关指标计算
% R2
R1(i) = 1 - norm(T_train(i, :) - T_sim1(i, :))^2 / norm(T_train(i, :) - mean(T_train(i, :)))^2;
R2(i) = 1 - norm(T_test (i, :) - T_sim2(i, :))^2 / norm(T_test (i, :) - mean(T_test (i, :)))^2;
disp(['输出:', num2str(i), ' 训练集数据的R2为:', num2str(R1(i))])
disp(['输出:', num2str(i), ' 测试集数据的R2为:', num2str(R2(i))])
% MAE
mae1(i) = sum(abs(T_sim1(i, :) - T_train(i, :))) ./ M ;
mae2(i) = sum(abs(T_sim2(i, :) - T_test (i, :))) ./ N ;
disp(['输出:', num2str(i), ' 训练集数据的MAE为:', num2str(mae1(i))])
disp(['输出:', num2str(i), ' 测试集数据的MAE为:', num2str(mae2(i))])
% MBE
mbe1(i) = sum(T_sim1(i, :) - T_train(i, :)) ./ M ;
mbe2(i) = sum(T_sim2(i, :) - T_test (i, :)) ./ N ;
disp(['输出:', num2str(i), ' 训练集数据的MBE为:', num2str(mbe1(i))])
disp(['输出:', num2str(i), ' 测试集数据的MBE为:', num2str(mbe2(i))])
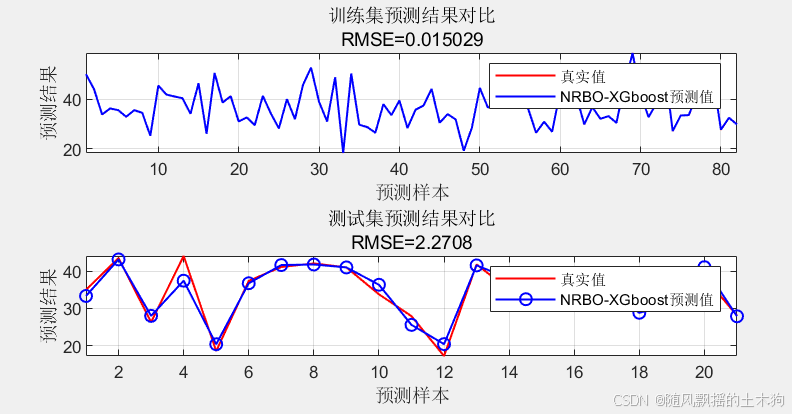
end二、模型训练结果:
输出:1 训练集数据的R2为:1
输出:1 测试集数据的R2为:0.90554
输出:1 训练集数据的MAE为:0.011996
输出:1 测试集数据的MAE为:1.6451
输出:1 训练集数据的MBE为:-1.1766e-06
输出:1 测试集数据的MBE为:0.27044

三、SHAP分析
1、生成随机数据
在本部分,生成一组合成输入数据用于SHAP分析。这种合成数据允许在受控和一致的方式下评估模型的特征贡献。步骤包括:
样本数量:脚本设置生成的合成样本数量为200(numSamples = 200).
特征范围: 定义操作参数在特定范围内,选择训练数据中各个输入变量的最大值和最小值
不需要手动再输入
matlab
VarMin=min(P_train');%各个参数下限
VarMax=max(P_train');%各个参数上限随机数据生成: 使用rand函数在定义的范围内为每个特征生成随机值,创建200个样本.
并行计算提高速度
matlab
parfor i=1:size(x,2)
x_shap(:,i)=VarMin(i)+ (VarMax(i) - VarMin(i)) * rand(numSamples, 1);
end此生成数据用于评估SHAP值并分析每个特征如何影响模型的预测。生成随机输入数据确保了SHAP分析中特征值的广泛范围,便于更全面地评估特征重要性.
2、计算SHAP值
该代码计算神经网络模型的SHapley Additive exPlanations(SHAP)值。SHAP值量化了每个特征对模型预测的贡献。该过程包括:
- 预分配SHAP值矩阵:初始化一个矩阵以存储所有输入样本和特征的SHAP值.
2.计算参考值:将参考值计算为所有输入特征的平均值,用于在排除或包含特征时进行比较.
3.计算SHAP值:对于每个输入样本,使用自定义的shapley_ann函数计算SHAP值,该函数迭代所有可能的特征组合以确定每个特征对预测的贡献.
4.自定义的shapley函数接受一个训练好的神经网络(net)、当前输入样本和参考值来计算每个特征的SHAP值。该方法提供了对单个特征如何影响模型输出的洞察.
matlab
% ------------------------------------
function shapValues = shapley_nrbo_xgb_fast(x_shap, refValue) %
% 使用Shapley公式计算SHAP值
如果有7个特征,则依次分析每个特征的累计贡献值
当分析第1个特征时,排除当前特征,即 1 0 0 0 0 0 0
迭代所有可能的特征组合
for i=1:2^(D-1)
xt1: 每个样本的特征变量输入值(处理后) 1*7
xt2: 计算的每个样本平均值(处理后) 1*7
xt3: 当分析不同特征时,将该特征值替换为平均值。 1*7
shapValues=shapValues+xgboost_test(xt3)-xgboost_test(xt2)
end3、可视化
------蜂群图:为每个特征创建散点图(蜂群图),显示所有样本的SHAP值。特征值被标准化并颜色编码以提高可解释性.
包括轴标签、网格、框以提高清晰度以及带有操作参数标签的颜色条. 此SHAP摘要图有助于理解哪些特征对模型的预测影响最大以及特征在样本中的变化情况.显示每个特征对模型预测的贡献。

-----条形图
计算平均绝对SHAP值:计算每个特征的绝对SHAP值的平均值,以量化每个特征的整体重要性.
条形图可视化:创建一个水平条形图,特征按其平均绝对SHAP值排序。这提供了模型中特征重要性的清晰、排序表示. 结果的SHAP摘要条形图有助于识别哪些特征对模型的预测影响最大.

四、代码获取
1.阅读首页置顶文章
2.关注CSDN
3.根据自动回复消息,私信回复"116期"以及相应指令,即可获取对应下载方式。