模拟退火算法和遗传算法都是常用于解决旅行商问题(TSP)的优化算法,它们在原理、搜索方式、收敛速度和适用场景等方面存在一些区别:
原理
- 模拟退火算法:模拟退火算法的灵感来源于固体退火原理。固体在加热后缓慢冷却时,原子会逐渐形成低能量的稳定结构。在算法中,通过一个初始的高温状态开始,随着温度的逐渐降低,算法以一定的概率接受较差的解,以此避免陷入局部最优解,最终找到全局最优解或近似最优解。
- 遗传算法:遗传算法借鉴了生物进化的原理,通过模拟自然选择和遗传机制,如选择、交叉和变异等操作,在解空间中进行搜索。算法维护一个种群,每个个体代表一个可能的解,通过不断地进化,使得种群中的个体逐渐向最优解靠拢。
搜索方式
- 模拟退火算法:模拟退火算法是一种单点搜索算法,它从一个初始解开始,通过不断地生成邻域解,并根据一定的概率接受这些解,逐步向最优解逼近。在搜索过程中,算法有一定的随机性,允许接受较差的解,从而跳出局部最优解。
- 遗传算法:遗传算法是一种多点搜索算法,它同时维护一个种群的多个解。通过选择操作,保留适应度较高的个体;通过交叉操作,将优良的基因组合传递给下一代;通过变异操作,引入新的基因,增加种群的多样性。
收敛速度
- 模拟退火算法:模拟退火算法的收敛速度相对较慢,尤其是在解空间较大的情况下。由于它需要在高温阶段进行大量的随机搜索,以避免陷入局部最优解,因此需要较长的时间才能收敛到一个较好的解。
- 遗传算法:遗传算法的收敛速度相对较快,尤其是在初始阶段。由于它同时搜索多个解,能够更快地找到一些较优的解。但是,在接近最优解时,遗传算法可能会陷入局部最优解,导致收敛速度变慢。
适用场景
- 模拟退火算法:模拟退火算法适用于解空间复杂、局部最优解较多的问题。由于它具有一定的随机性,能够跳出局部最优解,因此在解决一些复杂的优化问题时表现较好。
- 遗传算法:遗传算法适用于解空间较大、具有一定的并行性和多样性的问题。由于它能够同时搜索多个解,并且通过交叉和变异操作增加种群的多样性,因此在解决一些大规模的优化问题时表现较好。
实现复杂度
- 模拟退火算法:模拟退火算法的实现相对简单,只需要定义好初始解、邻域解的生成方式和接受概率即可。但是,模拟退火算法的参数调整比较困难,如初始温度、冷却速率等,这些参数的选择会影响算法的性能。
- 遗传算法:遗传算法的实现相对复杂,需要定义好种群的初始化、选择、交叉和变异等操作。但是,遗传算法的参数调整相对容易,如种群大小、交叉概率和变异概率等,这些参数的选择对算法的性能影响较小。
综上所述,模拟退火算法和遗传算法在解决旅行商问题上各有优缺点。在实际应用中,可以根据问题的特点和需求选择合适的算法。如果问题的解空间复杂、局部最优解较多,可以选择模拟退火算法;如果问题的解空间较大、具有一定的并行性和多样性,可以选择遗传算法。
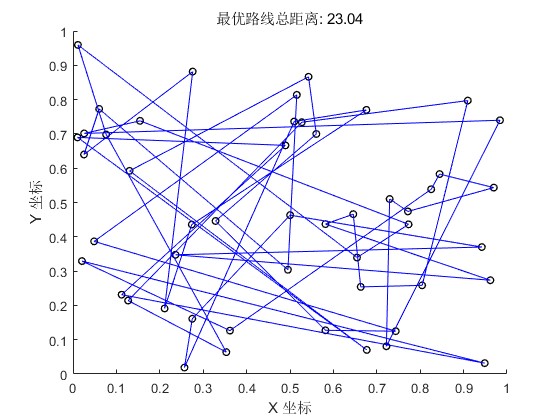
Matlab
% 随机生成 50 个城市的坐标
numCities = 50;
cities = rand(numCities, 2);
% 计算城市之间的距离矩阵
distMatrix = pdist2(cities, cities);
% 遗传算法参数设置
populationSize = 100; % 适当增大种群大小以提高搜索能力
numGenerations = 500; % 适当增加迭代代数以提高解的质量
mutationRate = 0.02;
% 初始化种群
population = zeros(populationSize, numCities);
for i = 1:populationSize
population(i, :) = randperm(numCities);
end
% 遗传算法主循环
for generation = 1:numGenerations
% 计算适应度
fitness = zeros(populationSize, 1);
for i = 1:populationSize
route = population(i, :);
route = [route route(1)]; % 回到起始城市
totalDistance = 0;
for j = 1:numCities
totalDistance = totalDistance + distMatrix(route(j), route(j+1));
end
fitness(i) = 1 / totalDistance; % 适应度为总距离的倒数
end
% 选择操作
selectionProb = fitness / sum(fitness);
newPopulation = zeros(populationSize, numCities);
for i = 1:populationSize
idx = randsample(populationSize, 1, true, selectionProb);
newPopulation(i, :) = population(idx, :);
end
% 交叉操作
for i = 1:2:populationSize
if rand < 0.8 % 交叉概率
parent1 = newPopulation(i, :);
parent2 = newPopulation(i+1, :);
[child1, child2] = orderCrossover(parent1, parent2);
newPopulation(i, :) = child1;
newPopulation(i+1, :) = child2;
end
end
% 变异操作
for i = 1:populationSize
if rand < mutationRate
newPopulation(i, :) = swapMutation(newPopulation(i, :));
end
end
population = newPopulation;
end
% 找到最优路线
[~, bestIndex] = max(fitness);
bestRoute = population(bestIndex, :);
bestRoute = [bestRoute bestRoute(1)]; % 回到起始城市
% 计算最优路线的总距离
totalDistance = 0;
for j = 1:numCities
totalDistance = totalDistance + distMatrix(bestRoute(j), bestRoute(j+1));
end
% 绘制最优路线
figure;
hold on;
plot(cities(:, 1), cities(:, 2), 'ko', 'MarkerSize', 5, 'LineWidth', 1); % 绘制城市
for j = 1:numCities
startCity = bestRoute(j);
endCity = bestRoute(j+1);
plot([cities(startCity, 1) cities(endCity, 1)], [cities(startCity, 2) cities(endCity, 2)], 'b-', 'LineWidth', 0.5);
end
title(sprintf('最优路线总距离: %.2f', totalDistance));
xlabel('X 坐标');
ylabel('Y 坐标');
hold off;
% 顺序交叉函数
function [child1, child2] = orderCrossover(parent1, parent2)
numCities = length(parent1);
% 随机选择交叉点
crossoverPoints = sort(randperm(numCities, 2));
startPoint = crossoverPoints(1);
endPoint = crossoverPoints(2);
% 初始化子代
child1 = zeros(1, numCities);
child2 = zeros(1, numCities);
% 复制交叉段
child1(startPoint:endPoint) = parent1(startPoint:endPoint);
child2(startPoint:endPoint) = parent2(startPoint:endPoint);
% 填充剩余部分
index1 = 1;
index2 = 1;
for i = 1:numCities
if ~ismember(parent2(i), child1(startPoint:endPoint))
if index1 < startPoint
child1(index1) = parent2(i);
index1 = index1 + 1;
elseif index1 >= endPoint + 1
child1(index1) = parent2(i);
index1 = index1 + 1;
end
end
if ~ismember(parent1(i), child2(startPoint:endPoint))
if index2 < startPoint
child2(index2) = parent1(i);
index2 = index2 + 1;
elseif index2 >= endPoint + 1
child2(index2) = parent1(i);
index2 = index2 + 1;
end
end
end
% 确保子代元素在有效范围内
child1 = child1(child1 > 0 & child1 <= numCities);
child2 = child2(child2 > 0 & child2 <= numCities);
% 补齐子代元素
missing1 = setdiff(1:numCities, child1);
missing2 = setdiff(1:numCities, child2);
child1 = [child1 missing1];
child2 = [child2 missing2];
end
% 交换变异函数
function mutatedRoute = swapMutation(route)
numCities = length(route);
% 随机选择两个位置
swapPositions = randperm(numCities, 2);
position1 = swapPositions(1);
position2 = swapPositions(2);
% 交换位置
mutatedRoute = route;
temp = mutatedRoute(position1);
mutatedRoute(position1) = mutatedRoute(position2);
mutatedRoute(position2) = temp;
% 确保变异后元素在有效范围内
mutatedRoute = mutatedRoute(mutatedRoute > 0 & mutatedRoute <= numCities);
% 补齐变异后元素
missing = setdiff(1:numCities, mutatedRoute);
mutatedRoute = [mutatedRoute missing];
end 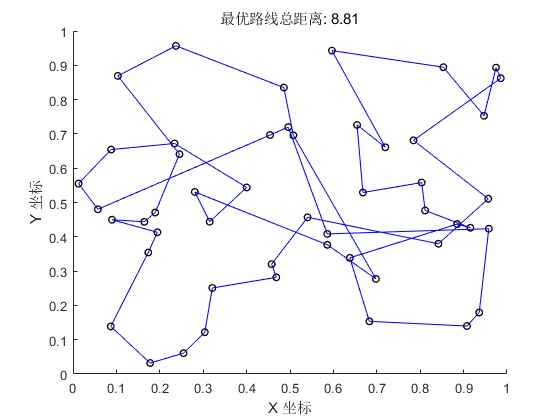
Matlab
% 随机生成 50 个城市的坐标
numCities = 50;
cities = rand(numCities, 2);
% 计算城市之间的距离矩阵
distMatrix = pdist2(cities, cities);
% 模拟退火算法参数设置
initialTemperature = 100; % 初始温度
finalTemperature = 0.1; % 最终温度
coolingRate = 0.99; % 冷却速率
numIterations = 1000; % 每个温度下的迭代次数
% 初始化当前解
currentRoute = randperm(numCities);
currentDistance = calculateTotalDistance(currentRoute, distMatrix);
% 初始化最优解
bestRoute = currentRoute;
bestDistance = currentDistance;
% 模拟退火主循环
temperature = initialTemperature;
while temperature > finalTemperature
for i = 1:numIterations
% 生成邻域解
newRoute = generateNeighborRoute(currentRoute);
newDistance = calculateTotalDistance(newRoute, distMatrix);
% 计算能量差
deltaDistance = newDistance - currentDistance;
% 判断是否接受新解
if deltaDistance < 0 || rand < exp(-deltaDistance / temperature)
currentRoute = newRoute;
currentDistance = newDistance;
% 更新最优解
if currentDistance < bestDistance
bestRoute = currentRoute;
bestDistance = currentDistance;
end
end
end
% 降温
temperature = temperature * coolingRate;
end
% 回到起始城市
bestRoute = [bestRoute bestRoute(1)];
% 绘制最优路线
figure;
hold on;
plot(cities(:, 1), cities(:, 2), 'ko', 'MarkerSize', 5, 'LineWidth', 1); % 绘制城市
for j = 1:numCities
startCity = bestRoute(j);
endCity = bestRoute(j + 1);
plot([cities(startCity, 1) cities(endCity, 1)], [cities(startCity, 2) cities(endCity, 2)], 'b-', 'LineWidth', 0.5);
end
title(sprintf('最优路线总距离: %.2f', bestDistance));
xlabel('X 坐标');
ylabel('Y 坐标');
hold off;
% 计算总距离的函数
function totalDistance = calculateTotalDistance(route, distMatrix)
numCities = length(route);
totalDistance = 0;
for i = 1:numCities - 1
totalDistance = totalDistance + distMatrix(route(i), route(i + 1));
end
totalDistance = totalDistance + distMatrix(route(numCities), route(1)); % 回到起始城市
end
% 生成邻域解的函数
function neighborRoute = generateNeighborRoute(route)
numCities = length(route);
% 随机选择两个位置
swapPositions = randperm(numCities, 2);
position1 = swapPositions(1);
position2 = swapPositions(2);
% 交换位置
neighborRoute = route;
temp = neighborRoute(position1);
neighborRoute(position1) = neighborRoute(position2);
neighborRoute(position2) = temp;
end