Matlab/Simulink - BLDC直流无刷电机仿真基础教程(六) - 波形解析专题P1
前言
本系列文章分享如何使用Matlab的Simulink功能来进行BLDC直流无刷电机的基础仿真;本篇文章将重点讲解模型中各种波形的机理,通过修改模型参数,结合理论与仿真结果,以说明BLDC电机的一些特性,部分专题视情况可能会再出专门文章进行分析。
在此感谢各位读者的支持,并欢迎交流。也希望本篇文章可以抛砖引玉,成为大家发表见解、提出问题的平台。
文章内容主要参考Matlab官网的BLDC仿真视频教程,主要是对官方视频教程的进一步详细说明,以及对BLDC电机控制原理、仿真过程部分问题点的简要讲解,希望大家通过此系列文章可以掌握Matlab电机仿真的基本技术,并在后续能够按照需要搭建更复杂的模型。
官方视频教程地址如下:
相关演示操作在Matlab2023b中进行。
一、运行时三相电压电流波形初步解析
在此前的系列文章中,我们搭建了带有PWM调制模块的BLDC速度闭环控制模型,接下来我们将会对运行过程中的电压电流波形进行初步的分析。
此处为了便于分析波形,我们修改速度参考量给定如下图所示,使模型在1s后速度维持在3000deg/s左右。

图片1.1 修改速度参考量给定
点击运行按钮,在运行完毕后打开连接在PID模块后面的示波器模块,可以看到PID控制器输出的占空比给定量如图所示。
在0~1s范围内,占空比呈现一个逐渐上升的趋势;1s后,此时仅需要维持BLDC电机转速稳定,因此占空比输出稳定在一个较小的数值。在1s左右时,占空比有一个比较剧烈的变化,我们可以猜想这个时候速度可能会略微超出3000deg/s。

图片1.2 PID控制器输出占空比
打开霍尔传感器模块中的角速度示波器,可以看到电机转速在0~1s内,均匀的由0deg/s上升到3000deg/s,之后维持在这个速度值左右,与我们设置的速度参考量的变化趋势一致。

图片1.3 转速波形变化情况
我们将角速度示波器中1s附近的波形放大,可以看到此时角速度数值超出了3000deg/s,大概在3014deg/s左右,有些微超调,与我们此前的猜想一致。

图片1.4 转速超调示意
接下来为了便于观察运行过程的电压电流波形,我们将三相电压传感器、三相电流传感器的输出连接到同一个示波器模块,这里为之命名为Voltage&Current。

图片1.5 电压电流同步显示
再次运行模型,运行完毕后打开这个示波器,我们放大后段速度稳定时间段的波形,可以看到如下图所示的波形。(请自行调整示波器显示窗口布局。)

图片1.6 三相电压电流波形
为了便于观察,我们将两相电压波形屏蔽掉,可以看到单独一相的电压波形变化趋势如下图所示。

图片1.7 单相电压波形与三相电流
我们简单标注一下电压波形的六个阶段以进行分析:在1、2阶段,目前显示的电压波形对应的逆变器状态是此相的下桥导通,因此电压数值一直是0;在3阶段,该相对应的状态是悬空状态,即逆变器的上桥和下桥都未导通,在这一阶段前面电压突然达到很高的数值的原因是电感续流,我们会在后续进行分析;4、5阶段,对应逆变器上桥打开,因此电压数值在100V左右;6阶段,再次变为悬空状态,前面同样由于电感续流,电压值变得很低,不过这张图并不明显。
此外,观察电流波形,我们可以看到,在1、2阶段,该相对应的电流数值是小于0的(下方同样是黄色的波形),而在3、6阶段悬空状态,电流都迅速的降低为0并保持;在4、5阶段,电流数值大于0。
各个阶段的三相电流都符合基尔霍夫电流定律,三相电流数值加起来为0;由于使用的是BLDC六步换相控制方式,各相电流呈现锯齿波变化;在1、2、4、5阶段,电压虽然保持在0或100左右,不过可以看到前面与黄色电流波形对应的是蓝色波形(1、4阶段),即此时黄色、蓝色波形对应电流数值加起来为0,而后面的阶段是红色波形(2、5阶段)。

图片1.7 单相电压波形分析
二、模型参数优化(如何设定求解器采样时间)
尽管刚刚的电压电流波形已经比较接近真实情况的波形,但细心的同学可以看到,我们的PID控制器输出的占空比数值非常奇怪。如下图所示,我们的占空比数值最大为0.035左右,而在1s后速度稳定的阶段,数值更是只有不到0.005,也就是占空比连1%都没有,这是明显异常的,也与我们刚刚看到的电压波形的占空比不对应。
真实的电路控制系统几乎不会专门输出这样的占空比,因为这种极小的占空比如果对应时间周期短的话,那么我们的开关器件可能每个周期大部分时间都工作在线性区来进行导通或关闭,会存在很大的损耗且有效输出将会与预期有很大偏差。

图片2.1 PID控制器占空比输出
接下来,我们要分析为何会出现这样的情况,来使我们的模型能够真正按照我们的预期来运行。
我们刚刚了解到,PID控制器输出的PWM占空比与电压电流波形实际对应的占空比不一致,因此我们可以考虑将输入给逆变器模块的开关状态信号显示出来,与电压波形进行比较。这里我们选择U相上桥MOSFET的开关信号进行显示,如下图所示引出信号连接到示波器模块上。

图片2.2 导通信号与电压波形同步显示
完成模块连接后,运行仿真模型,并打开刚刚放置的示波器模块,选择合适时间位置的波形进行放大观察。此时可以看到上方稠密的PWM信号波形与下方的电压波形大体对应上了。

图片2.3 导通信号与电压波形
继续放大波形,我们看到上方的PWM波形给定一个极短时间的高电平后,下方的电压波形就会相应的维持一段时间高电平,这一点出乎意料。

图片2.4 电压波形与导通信号不一致
我们使用示波器显示界面的游标功能,测量电压波形高低变化边缘对应的最后一个PWM高电平信号时间与电压波形切换到低电平的时间,可以看到这段时间大概是100us左右;仅仅从100us数值上来看,我们知道这个数值是PWM的周期,也是现在设定的PID环路控制周期,同时也是求解器设置的采样时间,表明其中必定有一个数值有问题,需要进一步修改来使得波形变化符合预期。

图片2.5 电压波形更新间隔测量
简单分析,我们知道PWM周期是100us,而占空比数值可以修改一个周期内输出为高的时间数值,从刚刚的波形图可以看到,占空比的设定实际是正常生效的;而PID环路的控制周期在这里尽管不合适,但其实并不会导致电压波形维持不恰当的时间,且PID控制器最终修改的是PWM模块的占空比,从波形中看也是对应的。
因此,我们需要修改的是求解器的采样时间,此前设定的1e-4,即100us数值并不恰当,这表示每隔100us才会对仿真模型的各个simscape模块进行更新,因此出现了电压波形以100us的时间间隔进行高低切换的情况。

图片2.6 求解器原始采样时间
这里通过查找资料学习,了解到我们需要设定求解器的采样时间更短,可以设定采样时间为1e-6,即1us,此时各个simscape模块将会以1us的间隔更新状态,基本满足我们的仿真需求。

图片2.7 求解器采样时间配置
由于此时采样时间大大缩短,如果继续采用原有的仿真配置(主要是仿真时间),将会运行特别长的时间;这里为了调整仿真运行时间,并使得我们的仿真模型更贴近真实,我们将会对仿真模型的参数进行较多的修改。
我们首先设置停止时间为0.2,以减小仿真运行耗时,接下来对于模型中各个模块的参数还需要进行一定修改。

图片2.8 仿真模型运行时间调整
- 为了在较短的时间间隔内能够观察到电机换相,我们需要提高电机的目标转速。
这里我们希望速度稳定后,对于六步换相的每一步,会有8个PWM周期进行控制,也就是完整的一轮六步换相耗时68100=4800us,即0.0048s完成一次六步换相(也就是电机转子旋转一圈),因此对应的角速度是1/0.0048=208.333rpm,转化为deg/s的单位即208.333*360=75000deg/s;所以这里我们修改速度参考量为数值是75000的constant模块。

图片2.9 修改速度参考量给定
- 控制周期方面,我们的PID控制器每次输出控制量后,正常都需要等待一段时间来让系统对控制量进行响应,之后再根据电机输出量与给定参考量的偏差信号进行调制。因此这里我们对PID控制器模块前面的延时模块进行修改,这里我们设定每隔2ms进行一次PID调节。

图片2.10 修改单位延迟模块采样时间
- 在PID参数方面,由于电机转速数值发生了较大变化,以及为了优化仿真效果,这里根据仿真情况调整了PI参数,放大为原先的十倍。

图片2.11 修改PID控制器模块参数
- 逆变器电压源方面,我们这里模拟运行一个由电网220V交流电供能的高压控制器,设定直流电压数值为311V(即交流电220V整流为稳定直流后的数值,220*(2^0.5)=311)。

图片2.12 电压源直流电压修改
- BLDC电机参数方面,修改磁链大小为0.04Wb,定子电感为0.001H,定子电阻为0.8欧姆。

图片2.13 BLDC电机定子电感与电阻修改
此外,修改电机转子惯量为0.02kg*m^2,修改转子初始转速为149500deg/s(想不到还可以设置这些吧)。

图片2.14 BLDC电机转子惯量与初始速度修改
- 接下来,我们修改连接在BLDC电机模块R端的惯性模块数值为0.02(此前为0.2)。
这里简要讲解一下为什么刚刚设置电机转子初始转速为149500deg/s,这个数值实际上是对于未带载,也就是单独对电机来说的,且实际含义是角动量,也就是说如果我们在电机输出轴增加了负载,那么这个角动量就需要分给负载,来使得负载能够与转子以相同的角速度旋转起来(这里假定负载和电机轴不会发生相对的旋转)。这里我们设定的电机转子惯量与惯性模块数值相同,因此角动量会被平分,同时我们为了让电机转速能够从略低于速度参考量的数值上升到速度参考量,所以数值要略低于75000*2=150000,所以我们选择149500。

图片2.15 惯性模块数值修改
为了方便观察PID控制器的输出情况,别忘了在PID控制器模块后面接一个scope示波器模块。

图片2.16 PID控制器模块输出连接示波器
点击运行按钮后,等待运行完毕,我们可以打开角速度示波器,看到电机速度按照我们的预期从74750deg/s上升到75000deg/s。

图片2.17 电机转子转速波形曲线
查看PID控制器输出的示波器,看到设定的PWM占空比在开始很快提高到1,之后略有波动后稳定在0.4左右,此时占空比的变化曲线就显得比较平滑,不像此前未调整模型参数前那样剧烈的波动;如果放大来看,将会看到占空比数值每隔0.002s发生一次更新,与我们前面设定的PID控制环路周期一致。

图片2.18 修改模型参数后的PID控制器占空比输出
进入到三相逆变器模块,可以看到三相电流在一开始很大,之后在接近0.05s时变得比较小,之后又维持在一个稍大一些电流幅值上,与前面的PID输出占空比波形的变化趋势基本一致。

图片2.19 修改模型参数后的三相电压波形
三相电压波形,可以看到在0.2s的时间范围内,由于电机转速现在设置的比较高,发生了很多次换相。

图片2.20 单相电压波形
在后面速度比较稳定的阶段,放大其中一段时间的电压波形,可以看到电压明显的六步换相的特征,与前面部分基本一致。

图片2.21 放大后的电压波形
继续观察之前将逆变器信号与电压波形信号连接在一起的示波器模块,可以看到现在PWM信号的高低变化与电压波形的高低变化基本一致了,解决了此前电压波形延迟变化的问题。

图片2.22 三相电压波形变化与开关信号一致
接下来,我们来测量一下完成一次六步换相需要的时间,使用示波器的游标功能,对齐电压波形左侧上升边沿,可以看到在速度基本稳定的阶段,两段电压波形间隔4.819ms,对应频率207.533Hz,与我们设定的208.333Hz基本一致。(考虑到光标放置的不是很准确,可以认为这种偏差主要是测量位置不当导致的。)

图片2.23 通过电压波形测量换相时间
我们对模型各个模块的参数进行了优化,后续我们将会在此基础上继续探索、讨论各种情况时电压波形的变化。
三、不同的PWM调制方式
在之前的文章中我们提到对于逆变电路,有不同的PWM调制方式;FOC控制框架一般使用SVPWM技术,一起被提到的一般还有SPWM等,不过这些调制方法不是这边六步换相控制的重点;这里我们会简要分析一下如下图所示的这些PWM调制方式的特点。

图片3.1 不同的PWM调制方式
从器件开通和关断损耗角度来看,a对应调制的方式的六个开关管都要进行脉宽调制,开关损耗器其它调制方式的两倍;b、c每只管子在导通期间,都有60°电角度受PWM信号调制,60°电角度保持恒导通,使得六个开关管的开通、关断损耗较为均匀的分配;d、e的六个开关管的开通、关断损耗集中在上桥或下桥的开关管,不过调制比较直观和简单,这里我们搭建的仿真模型使用的就是d对应的H_PWM-L_ON的调制方式。
按照输出极性来区分,其中a对应的调制方式属于双极性脉宽调制,逆变器输出电压极性会发生变化,电流脉动比较大,一般很少采用;而b~e属于单极性脉宽调制。
这里我们在之前的PWM调制策略外,再搭建一个a对应的PWM调制策略(也就是官方系列视频中的调制策略),并对比两者的区别。
按照本人了解到的一些资料内容,这里a对应的H_PWM-L_PWM应当是一种比较简单的双极性PWM互补输出的模式,当一相(称为A相)上桥打开时,对应另一相(B相)下桥导通;之后PWM一路的高电平输出完毕后,另一路在经过死区延时等处理后,也开始输出高电平,此时A相的下桥开始导通,B相的上桥导通。
也就是说这种PWM控制模式下,一个相位的处理中,四个MOSFET开关管都会进行导通、关断的切换。这里借用论文Expansion of Operating Speed Range of High-Speed BLDC Motor Using Hybrid PWM Switching Method Considering Dead Time 中的一张图片简单展示一下。
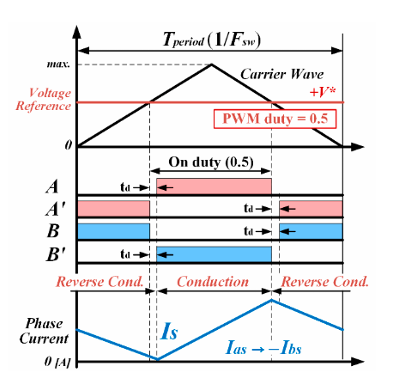
图片3.2 H_PWM-L_PWM调制方式示意图
接下来,我们要在模型中实现这样的PWM调制方式。打开换相逻辑模块,搭建如下图所示的一组换相逻辑表。

图片3.3 新搭建的换相逻辑表
取消之前的换相逻辑表的连接,连接新搭建的换相逻辑表,此时我们的模型如下图所示,注意红框标记部分的连接。

图片3.4 新的换相逻辑模块示意图/font>
我们前面提到,H_PWM-L_PWM的调制方式电流波动会比较大,相应地,转矩也会有较大的波动;这里我们索索Ideal Torque Sensor,即理想转矩传感器,将其拖动到右侧模型中。

图片3.5 Ideal Torque Sensor 理想转矩传感器模块
接下来我们按照如下图所示连接理想转矩传感器,将其R端口与BLDC电机模块的R端口进行连接,C端口则连接上之前放置的惯性模块、理想转矩源模块。
这里简单讲解一下为什么惯性模块要放到C端口后面,理想转矩传感器模块测量的是R端口、C端口表示的两个旋转轴之间的扭矩,我们现在想要测得的是电机R端口输出的转矩数值,这里的转矩将会作用到惯性模块、理想转矩源模块;我们可以将理想转矩传感器模块想象成是一种体重秤,R端口是我们放置体重秤的地面,C端口则是人站立的地方;如果我们把惯性模块放在R端口侧,就相当于人把体重秤顶到了头上,是无法正常测量到人的体重的。

图片3.6 连接理想转矩传感器模块
完成模块连接后,点击运行,这里我们首先来回顾一下之前搭建的H_PWM-L_ON的控制效果。
如下图所示是转速的波形曲线。

图片3.7 H_PWM-L_ON调制方式对应转速波形
PID控制器占空比输出。

图片3.8 H_PWM-L_ON调制方式对应PID控制器输出
刚刚搭建的理想转矩传感器模块的输出。

图片3.9 H_PWM-L_ON调制方式对应输出转矩波形
为便于后续比较转矩波动情况,我们放大0.16~0.20s的转矩波形。

图片3.10 放大转矩波形
继续放大后续的几个波形,可以看到输出转矩的波形是一种锯齿波,这也印证了为什么说BLDC电机六步换相控制方法相比于FOC有明显的转矩脉动。

图片3.11 进一步放大后的转矩波形
接下来,是刚刚搭建的H_PWM-L_PWM调制方法的控制效果,下方是转速波形曲线,可以看到由于这种调制方法是双极性调制,转速可以短时间内进行加速、减速的控制,因此波动更快速一些,波动幅值也更大。

图片3.12 H_PWM-L_PWM调制方式对应转速波形
PID控制器输出占空比也有一定震荡。

图片3.13 H_PWM-L_PWM调制方式对应PID控制器输出
此时对应的理想转矩传感器模块波形如下图所示。

图片3.14 H_PWM-L_PWM调制方式对应转矩输出
我们同样放大0.16~0.20时间范围的转矩波形。

图片3.15 放大转矩波形
放大后面几个波形的曲线,可以看到单独一个锯齿的幅值要比之前的要大不少,印证了H_PWM-L_PWM调制方式转矩脉动更大的预期。

图片3.16 进一步放大转矩波形
四、逆变器电路续流分析
在本系列文章的第四篇中,为了使得电压、电流波形比较贴近实际,我们在MOSFET模块中添加了体二极管,使用默认参数。

图片4.1 MOSFET模块体二极管默认参数
添加体二极管后,从相电压波形中可以看到,如下图所示的红色方框对应的时间段,电压突然变得很高或是变为0,这就是续流发生的时间。在前面逆变器状态由下桥导通切换为悬空态时,电压将会达到一个较高的数值;由上桥导通切换为悬空态时,电压将会降低到0V左右。

图片4.2 六步换相续流示意图
接下来,我们对其机理进行一个简要的分析。
如下图所示是我们的三相逆变器电路,根据不同的开关状态信号,六个MOSFET开关管将会进行导通、关断的处理。

图片4.3 三相逆变器模块示意图
这里,我们假定一开始V相上桥导通,U相下桥导通,此时电流的流向如下图中红色箭头所示。

图片4.4 UL-VH对应电流流向
之后,U相变为悬空状态,V相上桥导通,W下桥导通,此时电流为从V相上桥向下,流经电机定子绕组后由W相下桥流入地。
不过在状态刚刚切换时,电机U相的电感中还在流经电流,存储有能量,我们知道电感的电流不能发生突变,因此这个时候U相在短时间依然有从定子绕组流向逆变电路的电流,也就是下图中黄色箭头所示。
此时由于U相上下桥均为导通,电流无法从MOSFET开关管直接流过,不过由于体二极管的存在,电流可以由二极管流过,这也是为什么我们一般将这样的二极管称作续流二极管;那么这个时候由于二极管导通压降很低,例如模型中的默认参数仅为0.8V,相线电压就是母线电压加上二极管导通压降,因此在短时间内(续流未完成,悬空相的电流不为0时),U相电压变得很高,接近母线电压。

图片4.5 U相续流示意图
现在考虑另一种悬空状态,一开始U相上桥导通,V相下桥导通,此时电流的流向如下图中红色箭头所示。

图片4.6 UH-VL对应电流流向
之后,U相又变为悬空状态,W相上桥导通,V下桥导通,此时电流为从W相上桥向下,流经电机定子绕组后由V相下桥流入地。
这个时候U相在短时间有从定子绕组流向逆变电路的电流,如下图中黄色箭头所示。(注意这里电流的方向不同,因此上下桥体二极管的导通状态也不同。)
此时相线电压为零电压(也就是地)减去体二极管导通电压,因此此时U相电压变得很低,接近于零电压。这就是为什么我们给逆变器模块各个MOSFET模块添加了体二极管后,能够看到每次相位变为悬空状态时,会看到相电压突然提高到接近母线电压或降低到接近零电压。

图片4.7 U相续流示意图
五、PID参数
PID参数对控制效果影响很大,这里我们搭建了一个较为完善的BLDC速度闭环控制模型,刚好可以在此基础上进行PID调参测试。
在调参之前,我们必须要建立好控制环路,选定好用于反馈的信号以及控制量的输出,并注意信号极性。此处我们已经确定了使用电机转子转速作为反馈信号,PID控制器的输出用于控制PWM模块的占空比,并且当电机转子转速小于给定参考转速时,提高PWM模块占空比,反之则降低。
这里我们将反馈的电机转子转速与PID控制器的输出连接到同一个示波器模块以方便观察。

图片5.1 PID控制器模块输出连接示波器
这里我们简单回顾一下下面这个经典的PID调参口诀,后面我们可以结合实际仿真情况,来验证这个口诀。
参数整定找最佳,从小到大顺序查
先是比例后积分,最后再把微分加
曲线振荡很频繁,比例度盘要放大
曲线漂浮绕大弯,比例度盘往小扳
曲线偏离回复慢,积分时间往下降
曲线波动周期长,积分时间再加长
曲线振荡频率快,先把微分降下来
动差大来波动慢,微分时间应加长
理想曲线两个波,前高后低四比一
一看二调多分析,调节质量不会低
在完成模块的连接后,我们先不修改PID控制器参数,点击运行,来查看原始PID参数对应的电机转子转速情况与PID控制器输出情况。
此时对应参数P为2e-2,参数I为5e-2。

图片5.2 P=2e-2,I=5e-2对应波形
我们首先对参数P进行调节测试:降低参数P,此时参数P为1e-2,参数I为5e-2。
可以看到这个时候PID控制器的输出以及电机转子转速的波形更平滑了,也就是曲线的震荡减轻了,不过可能效果还不够突出。

图片5.3 P=1e-2,I=5e-2对应波形
继续调节参数P:降低参数P,此时参数P为2e-3,参数I为5e-2。
如下图所示,可以看到转速调节速度慢了很多,超调明显。也就对应了"曲线漂浮绕大弯,比例度盘往小扳",这里的"比例度盘"是应该是化工领域的一种仪器仪表,比例度盘越小,对应的就是这里的参数P越大,这一点要注意。因此面对这种情况,我们提高参数P(也就是恢复原本的数值),将会改善这种波形。

图片5.4 P=2e-3,I=5e-2对应波形
接下来,提高参数P,此时参数P为8e-2,参数I为5e-2。
如下图所示,验证了"曲线震荡很频繁,比例度盘要放大",此时我们的参数P有点太大了,导致PID控制器输出、电机转子转速频繁震荡,要适当降低参数P。

图片5.5 P=8e-2,I=5e-2对应波形
现在,我们来对参数I进行测试:降低参数I,此时参数P为2e-2,参数I为0。
可以看到由于积分效应被取消(或是积分参数很小的情况下,短时间波形也会比较相似),我们的电机转子转速出现了稳态误差,最终没有达到75000deg/s的转速,而是低了一些。
这一点其实也可以这样理解:我们的PID控制器现在只有P参数,而只有存在误差时,PID才会输出不为0的占空比;如果我们的转速和给定参考转速完全一致,那么误差为0,相应地,PID控制器输出占空比为0,此时电机又会逐渐减速,直到转速又与给定参考转速相差一定数值,此时PID控制器输出的占空比刚好足够电机转速保持稳定,然而也使得这个速度的偏差一直存在下来。
这种情况也对应了口诀中"曲线偏离回复慢,积分时间往下降",积分时间越低,对应到我们的模型就是参数I越大,此时我们模型的电机转速长时间偏离参考转速值,需要I参数有一定的数值。

图片5.6 P=2e-2,I=0对应波形
继续对参数I进行测试:提高参数I,此时参数P为2e-2,参数I为5e-1。
对应口诀"曲线波动周期长,积分时间再加长",此时我们的模型中电机转子转速超出了给定参考转速较大幅值后,又花了比较长的时间才慢慢降低下来,表明积分时间需要加长,也就是适当减小参数I。

图片5.7 P=2e-2,I=5e-1对应波形
口诀其它部分内容此处不再赘述,此外对于PI参数的调节,还可以根据模型的传递函数直接进行计算来选取,不过这部分博主也还需要学习了解,暂时不做讲解。
六、参控量斜坡给定
有较多代码调试经验的同学,将会知道在代码中,如果控制量给定,例如转速等,发生了很大的变化,往往不会将这样大的变化直接输入给控制器。而是使用斜坡函数等,来使得控制量逐渐上升,而避免参考量突变,进而也减轻了超调的现象。
这里我们使用重复序列模块,设置从0~0.1s内的速度参考量由74750逐渐升高到75000,而后维持在这一数值,以模拟参考量的斜坡渐变方式给定。

图片6.1 转速参考量斜坡给定
此时点击运行按钮,运行完毕后观察PID控制器输出和电机转子转速的波形情况,可以看到此时PID控制器输出变化比较均匀,没有像之前一样很快的达到1,并且电机转子转速的超调情况也大大减轻。

图片6.2 斜坡方式给定转速参考量后的占空比输出与转速波形
仔细观察电机转子转速波形,可以发现此时超调减弱后,又出现了误差减小缓慢的情况,在0.2s的时刻,转速依然没有达到75000deg/s;运用我们刚刚学习的PI参数调节方法,我们此时可以适当提高参数I,这里我们修改参数I为1e-1,并再次运行模型。

图片6.3 提高PID控制器I参数
此时我们可以看到电机转速比较快地接近了75000deg/s的转速,符合我们的预期。

图片6.4 修改I参数后的占空比输出与转速波形
本篇文章中,我们讲解了关于BLDC速度闭环控制模型参数优化、PWM调制方式以及PI参数调节的相关内容。其中PWM调制方式以及PI参数、参考量斜坡给定方法都属于我们搭建实际控制系统之前就要做好的工作,这些属于控制系统内部的一些可由我们进行优化的内容,务必要尽力提前做好。
下一章我们将会讲解一些外部参数变化或异常对电机控制效果的影响。
参考链接
电机控制杂谈(5)------搭建标准的电机控制模型(设置恰当的采样频率、PWM开关频率、控制频率以及电机仿真步长)
控制系统外环带宽高于内环带宽会怎么样?
BLDC控制系统中PWM调制方式分析与比较
Expansion of Operating Speed Range of High-Speed BLDC Motor Using Hybrid PWM Switching Method Considering Dead Time
基于MATLAB/Simulink的BLDC建模与仿真分析
BLDC驱动基础篇:补充端电压的来龙去脉 - 嵌入式BLDC的文章 - 知乎
《重载条件下无刷直流电机无位置传感器驱动换相续流影响的分析及其补偿》
《基于无位置传感器的无刷直流电机换相续流研究》
黄文鑫详解经验法PID参数调节口诀
无刷直流电机控制中的Ramp函数
斜坡发生器(也称为斜坡函数或斜坡控制)是一种用于渐进式地改变系统中某个参数或状态的算法