前言
🌟🌟本期讲解关于力扣的几篇题解的详细介绍~~~
🌈感兴趣的小伙伴看一看小编主页:GGBondlctrl-CSDN博客
🔥 你的点赞就是小编不断更新的最大动力
🎆那么废话不多说直接开整吧~~

目录

📚️1.N叉树的层序遍历
🚀1.1题目描述
给定一个 N 叉树,返回其节点值的层序遍历。(即从左到右,逐层遍历)。
树的序列化输入是用层序遍历,每组子节点都由 null 值分隔(参见示例)。
如下图所示:

输入:root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14]
输出:[[1],[2,3,4,5],[6,7,8,9,10],[11,12,13],[14]]
层序遍历就是从上到下,从左到右依次进行遍历操作;
🚀1.2思路讲解
本题的主要思路就是使用队列来进行操作,为啥呢?假如我们将根结点放入某个数据结构中,然后再使用这个节点后,肯定要进行出的操作,但是他还有其他子结点,那么就要添加进去,但是层序遍历时从左到右依次进行遍历,一般来说二叉树这类题基本就是两种栈和队列,那么先入的节点的下一层子结点肯定也是先入队列,所以我们先入的节点要先出(即先入的节点,先出(对应的子结点才可以满足从左到右的遍历方式))所以使用队列比较合适;
具体的思路分析
1.入队列,我们在队列不为空的时候进行入队列操作
2.出队列,我们要根据这层的数据数量来决定出几个元素来进行保存
3.出队列要进行子结点的入队列操作
4.队列为空即可跳出循环
具体的操作如下所示:

🚀1.3题目代码
具体的代码如下所示:
java
class Solution {
public List<List<Integer>> levelOrder(Node root) {
List<List<Integer>> ret = new ArrayList<>();
Queue<Node> queue = new LinkedList<>();
//非空判断
if(root == null){
return ret;
}
queue.offer(root);
//记录每层的数量
int count = 0;
//入队列,出队列核心代码
while(!queue.isEmpty()){
count = queue.size();
List<Integer> temp = new ArrayList<>();
for(int i = 0; i < count ; i++){
//出队列
Node node = queue.poll();
temp.add(node.val);
for(Node t : node.children){
queue.offer(t);
}
}
ret.add(temp);
}
return ret;
}
}解释:
处理基础的非空判断,在队列非空的时候一直进行循环操作,我们使用size()来记录需要出队列的次数,然后将出节点的子结点通过方法入队列,每次循环后,将我们的保存的数据放入最终的返回的数据结构中去;
📚️2.二叉树锯齿形遍历
🚀2.1题目描述
给你二叉树的根节点 root ,返回其节点值的 锯齿形层序遍历 。(即先从左往右,再从右往左进行下一层遍历,以此类推,层与层之间交替进行)
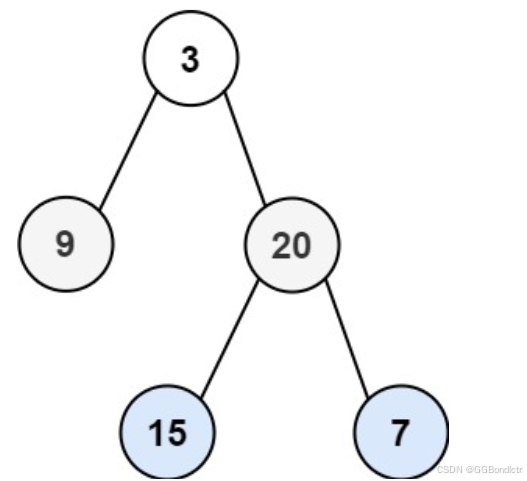
输入:root = [3,9,20,null,null,15,7]
输出:[[3],[20,9],[15,7]]
其实就是一个S形的遍历的方式而已,对于普通的层序遍历进行了一点小变化操作
🚀2.2思路讲解
开始小编在进行分析的时候,是将节点进行不同的层级来进行不同顺序的入队列操作
若为奇数:先入左孩子,再入右孩子
若为偶数:先入右孩子,再入左孩子
但是此时就有一个巨大的问题:孩子的位置改变了,那么对应的子结点也会跟着变化,那么就会越来越乱;
但是结题思路就是,在出队列后,保存数据元素的时候,根据不同的层级进行逆序不就解决了吗?
具体的思路:
1.入队列,在队列不为空的情况下一直循环
2.出队列,还是判断本层的数据量
3.将出去节点的左右孩子进行判断后进行入队列操作
4.保存元素后,根据层级进行是否逆序的判断
其实本题就是对于上一题的一个小小的变化:
这里的判断是否进行逆序判断我们可以设置一个标志位,假如是bool类型,那么我们可以根据true或者false来进行判断;
或者是一个整型,是奇数我们就....然后加1,是偶数我们......,大概就是这种思路
🚀2.3题目代码
具体的代码如下所示:
java
class Solution {
public List<List<Integer>> zigzagLevelOrder(TreeNode root) {
//非空校验
List<List<Integer>> ret = new ArrayList<>();
if(root == null){
return ret;
}
//设置一个bool类型标志位
boolean bool = false;
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
while(!queue.isEmpty()){
int count = queue.size();
List<Integer> temp = new ArrayList<>();
for(int i =0; i < count;i++){
//出队列
TreeNode node = queue.poll();
temp.add(node.val);
if(node.left != null){
queue.offer(node.left);
}
if(node.right != null){
queue.offer(node.right);
}
}
if(bool == false){
ret.add(temp);
bool =true;
}else{
//进行逆序的操作
Collections.reverse(temp);
ret.add(temp);
bool =false;
}
}
return ret;
}
}解释:
本题和上一题的差距不大,小编这里使用的是布尔类型的变量来进行操作的,在bool为真的时候进行翻转操作: Collections.reverse(temp)数组的翻转操作;然后再进行入队列的时候要注意子结点的为空的情况,本题大致和上题的结题思路基本是一致的的;
📚️3.二叉树最大宽度
🚀3.1题目描述
给你一棵二叉树的根节点 root ,返回树的 最大宽度 。
树的 最大宽度 是所有层中最大的 宽度 。
每一层的 宽度 被定义为该层最左和最右的非空节点(即,两个端点)之间的长度。将这个二叉树视作与满二叉树结构相同,两端点间会出现一些延伸到这一层的 null 节点,这些 null 节点也计入长度。
题目数据保证答案将会在 32 位 带符号整数范围内。

输入:root = [1,3,2,5,3,null,9]
输出:4
解释:最大宽度出现在树的第 3 层,宽度为 4 (5,3,null,9)
其实就是获取最大的宽度,当然也要将两个最大宽度节点中的null节点算入我们的宽度长度;
🚀3.2思路讲解
首先这里也是层序遍历的一个变化,我们可以保存每个节点,以及每个节点的数字下标,那么此时每一层的宽度就是队列中第一个元素下标以及最后一个元素下标
注意:本题的下标使用的公式就是2*x + 1(左节点)2*x + 2(右节点)
那么此时我们每一个得到的队列,就是一层数据,那么就可以进行宽度的计算操作了;
🚀3.3题目代码
具体的代码如下所示:
java
class Solution {
public int widthOfBinaryTree(TreeNode root) {
//使用数组去存储我们的节点以及对应的下标数
List<Pair<TreeNode,Integer>> ret = new ArrayList<>();
//默认为1
ret.add(new Pair<TreeNode,Integer>(root,1));
int result = 0;
while(!ret.isEmpty()){
//记录最大的宽度
Pair<TreeNode,Integer> root1 = ret.get(0);
Pair<TreeNode,Integer> root2 = ret.get(ret.size() - 1);
result = Math.max(result,root2.getValue() - root1.getValue() + 1);
List<Pair<TreeNode,Integer>> temp = new ArrayList<>();
//入队列
for(Pair<TreeNode,Integer> q : ret){
TreeNode node = q.getKey();
int index = q.getValue();
if(node.left != null){
temp.add(new Pair<TreeNode,Integer>(node.left,2*index + 1));
}
if(node.right != null){
temp.add(new Pair<TreeNode,Integer>(node.right,2*index + 2));
}
}
//模拟出队列,覆盖原来数据
ret = temp;
}
return result;
}
}解释:
这里主要就是对于Pair的使用,在保存数据的时候,要对于节点和下标进行保存的操作,并且我使用的即数组来模拟队列,创建一个新的数组,然后进行覆盖的操作将旧数组进行覆盖;
📚️4.总结
本期小编主要是对于力扣中关于层序遍历的题型讲解,主要包括N叉树层序遍历,二叉树锯齿形遍历,以及二叉树最大宽度计算~~~
题目来源:
103. 二叉树的锯齿形层序遍历 - 力扣(LeetCode)
🌅🌅🌅~~~~最后希望与诸君共勉,共同进步!!!

💪💪💪以上就是本期内容了, 感兴趣的话,就关注小编吧。
😊😊 期待你的关注~~~
