STM32实现九轴IMU的卡尔曼滤波

在嵌入式系统中，精确的姿态估计对于无人机、机器人和虚拟现实等应用至关重要。九轴惯性测量单元（IMU）通过三轴加速度计、陀螺仪和磁力计提供全面的运动数据。然而，这些传感器数据常伴随噪声和漂移，单独使用无法满足高精度需求。卡尔曼滤波作为一种强大的传感器融合算法，能够有效结合多传感器数据，估计系统状态。

九轴IMU通常由以下三部分组成：

三轴加速度计：测量线性加速度，可用于确定重力方向和线性运动
三轴陀螺仪：测量角速度，用于检测旋转运动
三轴磁力计：测量地磁场，提供绝对方向参考

这些传感器的互补特性使得传感器融合成为必要。融合算法通过结合各传感器数据，克服单一传感器的局限性，提供更准确的姿态估计。

由于各传感器存在固有缺陷（如陀螺仪漂移、加速度计噪声、磁力计干扰），单独使用无法提供可靠的姿态估计。传感器融合通过数学模型整合多传感器数据，生成更精确的估计结果。常用的融合算法包括互补滤波和卡尔曼滤波，其中卡尔曼滤波因其理论最优性广泛应用于姿态估计。

卡尔曼滤波是一种递归算法，用于从噪声测量中估计动态系统的状态。它假设系统是线性的，噪声为高斯分布。卡尔曼滤波包括两个主要步骤：

预测步骤：根据系统模型预测下一时刻的状态和协方差。
更新步骤：利用新测量值修正预测状态，计算卡尔曼增益以平衡预测和测量。

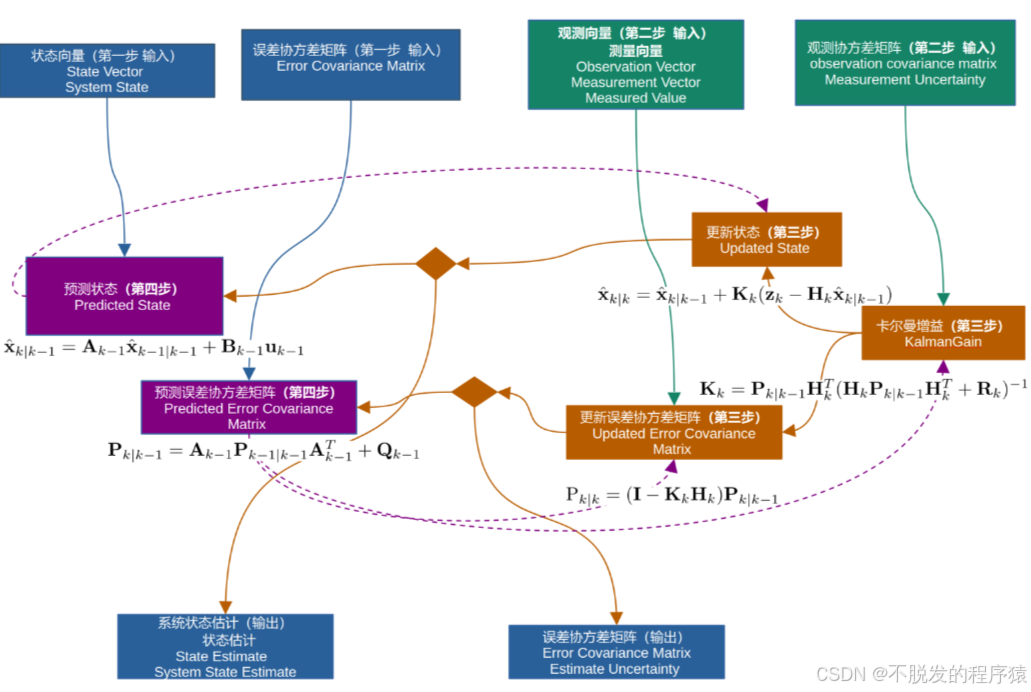
对于卡尔曼滤波的原理，我们不再细究，网上有很多资料，本篇文章主要讲解嵌入式工程师如何使用代码实现卡尔曼滤波。

在STM32微控制器上实现九轴IMU的卡尔曼滤波需要选择一款支持浮点运算单元（FPU）的STM32微控制器（如STM32F4系列），以高效处理矩阵运算。将九轴IMU（如MPU9250）通过I2C或SPI接口连接到STM32开发板。确保电源稳定，通信线路正确连接。

以下是九轴IMU卡尔曼滤波的核心实现：

cpp 复制代码

// 状态向量：[q0, q1, q2, q3, bgx, bgy, bgz]
float state[7];

// 状态协方差矩阵 P (7x7)
float P[49];

// 过程噪声协方差矩阵 Q (7x7)
float Q[49];

// 观测噪声协方差矩阵 R (6x6)：3个加速度计和3个磁力计
float R[36];

// 状态转换矩阵 F (7x7)
float F[49];

// 观测矩阵 H (6x7)
float H[42];

// 卡尔曼增益 K (7x6)
float K[42];

// 预测状态
float state_pred[7];

// 预测协方差
float P_pred[49];

// 残差
float y[6];

// S = H*P*H^T + R
float S[36];

// 初始状态
void init_state(float initial_q[4], float initial_bg[3]) {
    // 初始化状态向量
    memcpy(state, initial_q, 4*sizeof(float));
    memcpy(state+4, initial_bg, 3*sizeof(float));
    
    // 初始化协方差矩阵 P
    memset(P, 0, 49*sizeof(float));
    P[0] = 0.01f; P[7] = 0.01f; P[14] = 0.01f; P[21] = 0.01f; // q的方差
    P[28] = 0.01f; P[35] = 0.01f; P[42] = 0.01f; // bg的方差
    
    // 初始化过程噪声协方差 Q
    memset(Q, 0, 49*sizeof(float));
    Q[0] = 0.001f; Q[7] = 0.001f; Q[14] = 0.001f; Q[21] = 0.001f; // q的噪声
    Q[28] = 0.0001f; Q[35] = 0.0001f; Q[42] = 0.0001f; // bg的噪声
    
    // 初始化观测噪声协方差 R
    memset(R, 0, 36*sizeof(float));
    R[0] = 0.1f; R[7] = 0.1f; R[14] = 0.1f; // 加速度计噪声
    R[21] = 0.1f; R[28] = 0.1f; R[35] = 0.1f; // 磁力计噪声
}

// 预测步骤
void predict(float gyro[3], float dt) {
    // 计算角速度四元数
    float omega[4] = {0, gyro[0], gyro[1], gyro[2]};
    float theta = sqrt(omega[1]*omega[1] + omega[2]*omega[2] + omega[3]*omega[3]) * dt;
    float axis[3];
    if (theta > 1e-6) {
        axis[0] = omega[1]/theta;
        axis[1] = omega[2]/theta;
        axis[2] = omega[3]/theta;
    } else {
        axis[0] = 0;
        axis[1] = 0;
        axis[2] = 0;
    }
    float dq[4] = {cos(theta/2), axis[0]*sin(theta/2), axis[1]*sin(theta/2), axis[2]*sin(theta/2)};
    
    // 预测四元数
    float q[4];
    quaternion_multiply(state, dq, q);
    quaternion_normalize(q);
    memcpy(state_pred, q, 4*sizeof(float));
    
    // 陀螺仪偏置保持不变
    memcpy(state_pred+4, state+4, 3*sizeof(float));
    
    // 计算状态转换矩阵 F
    // (这里简化为恒等矩阵，实际应用中需要正确计算)
    memset(F, 0, 49*sizeof(float));
    for(int i=0; i<7; i++) F[i*8] = 1.0f;
    
    // P_pred = F*P*F^T + G*Q*G^T
    // (这里简化为P_pred = P + Q)
    for(int i=0; i<49; i++) P_pred[i] = P[i] + Q[i];
    
    // 更新状态和协方差
    memcpy(state, state_pred, 7*sizeof(float));
    memcpy(P, P_pred, 49*sizeof(float));
}

// 更新步骤
void update(float acc[3], float mag[3], float ref_mag[3]) {
    // 计算期望的加速度计测量值
    float q_inv[4];
    quaternion_conjugate(state, q_inv);
    float expected_acc[4] = {0, 0, 0, -1};
    quaternion_multiply(state, expected_acc, expected_acc);
    quaternion_multiply(expected_acc, q_inv, expected_acc);
    expected_acc[1] /= expected_acc[0];
    expected_acc[2] /= expected_acc[0];
    expected_acc[3] /= expected_acc[0];
    
    // 计算期望的磁力计测量值
    float expected_mag[4];
    quaternion_multiply(state, ref_mag, expected_mag);
    quaternion_multiply(expected_mag, q_inv, expected_mag);
    expected_mag[1] /= expected_mag[0];
    expected_mag[2] /= expected_mag[0];
    expected_mag[3] /= expected_mag[0];
    
    // 组合观测向量
    float z[6] = {
        acc[0], acc[1], acc[2],
        mag[0], mag[1], mag[2]
    };
    
    float h[6] = {
        expected_acc[1], expected_acc[2], expected_acc[3],
        expected_mag[1], expected_mag[2], expected_mag[3]
    };
    
    // 计算残差
    for(int i=0; i<6; i++) y[i] = z[i] - h[i];
    
    // 计算观测矩阵 H
    // (这里简化为恒等矩阵，实际应用中需要正确计算)
    memset(H, 0, 42*sizeof(float));
    for(int i=0; i<6; i++) H[i*8 + i] = 1.0f;
    
    // 计算 S = H*P*H^T + R
    // (这里简化为 S = H*P*H^T + R)
    memset(S, 0, 36*sizeof(float));
    for(int i=0; i<6; i++) {
        for(int j=0; j<7; j++) {
            if (H[i*7 + j] == 0) continue;
            for(int k=0; k<6; k++) {
                if (H[k*7 + j] == 0) continue;
                S[i*6 + k] += H[i*7 + j] * P[j*7 + k] * H[k*7 + j];
            }
        }
    }
    for(int i=0; i<36; i++) S[i] += R[i];
    
    // 计算卡尔曼增益 K = P*H^T*S^{-1}
    // (这里简化为 K = P*H^T / (H*P*H^T + R))
    memset(K, 0, 42*sizeof(float));
    for(int i=0; i<7; i++) {
        for(int j=0; j<6; j++) {
            float sum = 0;
            for(int k=0; k<7; k++) {
                sum += P[i*7 + k] * H[j*7 + k];
            }
            K[i*6 + j] = sum / S[j*6 + j];
        }
    }
    
    // 更新状态
    for(int i=0; i<7; i++) {
        float sum = 0;
        for(int j=0; j<6; j++) {
            sum += K[i*6 + j] * y[j];
        }
        state[i] += sum;
    }
    
    // 更新协方差
    memset(P, 0, 49*sizeof(float));
    for(int i=0; i<7; i++) {
        for(int j=0; j<7; j++) {
            float sum = 0;
            for(int k=0; k<6; k++) {
                sum += K[i*6 + k] * H[k*7 + j];
            }
            P[i*7 + j] = (1 - sum) * P_pred[i*7 + j];
        }
    }
}

以下是完整的STM32实现框架：

cpp 复制代码

#include "stm32f10x.h"

// 定义MPU9250和HMC5883L的I2C地址
#define MPU9250_ADDR 0x68
#define HMC5883L_ADDR 0x1E

// MPU9250寄存器定义
#define PWR_MGMT_1 0x6B
#define SMPLRT_DIV 0x19
#define CONFIG 0x1A
#define GYRO_CONFIG 0x1B
#define ACCEL_CONFIG 0x1C
#define INT_ENABLE 0x38
#define PWR_MGMT_2 0x3B

// HMC5883L寄存器定义
#define HMC5883L_CTRL_REG_A 0x0A
#define HMC5883L_CTRL_REG_B 0x0B

// 状态向量：[q0, q1, q2, q3, bgx, bgy, bgz]
float state[7];

// 状态协方差矩阵 P (7x7)
float P[49];

// ... 其他变量声明

// I2C写操作
void i2c_write(uint8_t addr, uint8_t reg, uint8_t value) {
    // 实现I2C写操作
}

// I2C读操作
uint8_t i2c_read(uint8_t addr, uint8_t reg) {
    // 实现I2C读操作
}

// 四元数乘法
void quaternion_multiply(float *q1, float *q2, float *result) {
    // 实现四元数乘法
}

// 四元数归一化
void quaternion_normalize(float *q) {
    // 实现四元数归一化
}

// 四元数共轭
void quaternion_conjugate(float *q, float *result) {
    // 实现四元数共轭
}

// MPU9250初始化
void mpu9250_init(void) {
    // 实现MPU9250初始化
}

// 从MPU9250读取加速度计数据
void read_accel(float *accel) {
    // 从MPU9250读取加速度计数据
}

// 从MPU9250读取陀螺仪数据
void read_gyro(float *gyro) {
    // 从MPU9250读取陀螺仪数据
}

// 从HMC5883L读取磁力计数据
void read_magnet(float *magnet) {
    // 从HMC5883L读取磁力计数据
}

// 初始化卡尔曼滤波器
void init_kalman(float initial_q[4], float initial_bg[3]) {
    // 初始化卡尔曼滤波器
}

// 卡尔曼滤波预测步骤
void kalman_predict(float gyro[3], float dt) {
    // 实现卡尔曼滤波预测步骤
}

// 卡尔曼滤波更新步骤
void kalman_update(float accel[3], float magnet[3], float ref_magnet[3]) {
    // 实现卡尔曼滤波更新步骤
}

int main(void) {
    // 初始化STM32外设
    // ...
    
    // 初始化MPU9250
    mpu9250_init();
    
    // 初始化卡尔曼滤波器
    float initial_q[4] = {1, 0, 0, 0}; // 初始姿态为0角度
    float initial_bg[3] = {0, 0, 0}; // 初始陀螺仪偏置为0
    init_kalman(initial_q, initial_bg);
    
    // 参考地磁场值(根据实际位置确定)
    float ref_magnet[3] = {0, 0, -1}; // 南极指向地心
    
    float gyro[3], accel[3], magnet[3];
    
    while(1) {
        // 读取传感器数据
        read_gyro(gyro);
        read_accel(accel);
        read_magnet(magnet);
        
        // 预测步骤
        float dt = 0.01; // 10ms采样周期
        kalman_predict(gyro, dt);
        
        // 更新步骤
        kalman_update(accel, magnet, ref_magnet);
        
        // 处理滤波结果
        // ...
        
        // 延时
        Delay_Ms(10);
    }
}

如果不想自己手写代码，可以使用STMicroelectronics的MotionFX库。

它是X-CUBE-MEMS1软件扩展的一部分，内置优化的卡尔曼滤波算法，支持6轴和9轴IMU融合。该库针对STM32微控制器优化，适合快速开发。

MotionFX库在不同STM32平台上的性能效果如下：

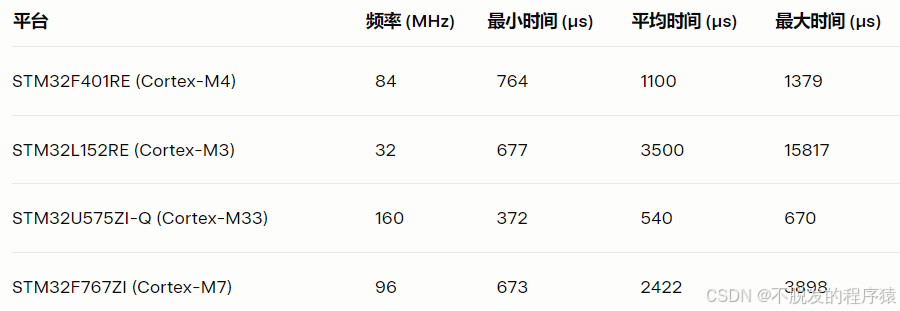
在STM32上实现九轴IMU的卡尔曼滤波是嵌入式系统中实现高精度姿态估计的有效方法。通过理解IMU的工作原理、卡尔曼滤波的理论以及系统建模，开发者可以从头实现EKF算法。或者，利用ST的MotionFX库可以显著简化开发流程，同时保持高性能。