目录
[2.1 信道编码](#2.1 信道编码)
原文：《DEEPPOLAR: Inventing Nonlinear Large-Kernel Polar Codes via Deep Learning》
2.问题的提出和背景
2.1 信道编码
信道编码是一种为传输添加冗余的技术 ，使其对通信信道添加的噪声具有鲁棒性 。更精确地说，设u=
表示我们希望传输的信息/消息比特块。代码由编码器和解码器对组成。
编码器 
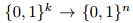，g（u）。码字通过调制 （例如二进制相移键控（BPSK））映射到实数/复数值。信道 表示为
，将码字X破坏为其有噪声的版本
。在接收到破坏的码字后，解码器fθ将消息比特估计为
。代码的性能 是使用标准错误度量（standard error metrics）来衡量的，如误码率（BER）或误块率（BLER）：
图2:通过深度学习进行信道编码
2.2.极化码
由Erdal Arıkan（Arikan，2009）提出，是第一个在保持低编码和解码复杂度的同时实现香农容量的确定性码结构。本节正式定义了Polar代码，并提出我们的方法。
极坐标编码
Polar码可以用**Polar（n，k，F）**来描述。这里，n是块长度（对于某个整数m，
），k是信息比特数，F表示"冻结"比特位置的集合。
通常，选择与极化引起的噪声最大的n-k比特信道对应的位置进行冻结。
- 极坐标编码器将信息比特
映射到二进制码字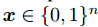 
。 - 极坐标码的基本构建块 是Plotkin变换：
。
一对输入比特（u，v）的映射（ mapping for a pair of input bits (u, v) ），可以用矩阵
,将（u0，u1）转换为
，其中
表示XOR运算。与编码理论文献一致，我们将这种构建块称为内核。通过取基核G2 的Kronecker积m次，得到块长度
的编码矩阵。
图3。
（a）使用标准2×2内核的Polar（4,3）编码结构。编码在Plotkin树上递归执行。
（b）使用4×4核的Polar（16,8）编码。
（c）DEEPOLAR（4,3，ℓ=2）用神经网络代替Plotkin-2×2中的异或运算。
（d） DEEPPOLAR（16,8，ℓ=4）：将DEEPOLAR编码扩展到高阶内核使我们能够实现良好的可靠性。我们是第一个探索这个设计空间的人
利用这种结构，可以通过在二叉树（称为Plotkin树）上递归坐标应用Plotkin变换 来有效地执行编码。
为了对消息比特块
进行编码，我们首先将它们嵌入到源消息向量：
由于消息块m仅在与I相关的索引处包含信息比特u，因此集合I称为信息集，其补码<complement >
称为冻结集<the frozen set>。我们通过一个小例子Polar（4,3）描述了Plotkin树上的编码，如图3（a）所示。
图3
（a）使用标准2×2内核的Polar（4,3）编码结构。编码在Plotkin树上递归执行。
这里，F={0}。考虑一个大小为k=3，u=[u0，u1，u2]的输入。在输入级别（深度1），我们冻结m0，即m0=0，并将u分配给其余位置。应用Plotkin变换
和
。在第二级，我们对这些向量协调应用相同的操作，即
和
。
最终的编码向量是来自第二级节点的输出的级联，即
。对于一般的（n，k）极坐标码，编码过程类似地进行到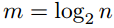
级。
极坐标解码
编码 消息被噪声信道 
破坏。连续抵消（SC）算法是极坐标码最有效的解码器之一，并且是渐近最优的。
- SC算法背后的基本原理是根据给定损坏码字y和先验解码比特
的条件似然性顺序解码每个消息比特
。
第i位的LLR可以计算为
SC解码在A中有详细描述👇。（或者查看我的另一篇博客：连续抵消解码器--Successive Cancellation decoder（SC 解码器）-CSDN博客）：
大内核Polar代码
由于信道极化现象，极性码在渐近块长度处是最优的（容量实现）。（Korada等人，2010）证明了用ℓ × ℓ 二元核 （ℓ>2）仍然会导致极化 ，前提是该矩阵在任何列置换下都是非奇异 的，并且不是上三角矩阵 。此外，如更好的缩放指数所示，已经发现了与传统极坐标码相比，在更短的块长度下实现容量的大核极坐标码（Fazeli&Vardy，2014；Fazeli等人，2020）。值得注意的是，内核大小必须扩展到8 才能超过Arikan的
内核，因为没有大小为4的线性内核提供改进的缩放指数 。这些内核以增加解码复杂度为代价，实现了更好的有限长度性能。
大核极性编码和解码 与传统极性码类似，通过ℓ × ℓ 内核。
- 一个示例：内核ℓ = 4 是G与自身的克罗内克积，G4=
。这是一个具有4个输入的Plotkin变换，称为Plotkin-4。我们通过一个（n=16，k=8）具有内核大小的代码示例来说明这一点，如图3所示，ℓ = 4 。
在该示例中，消息u在信息位置I =
={7，9，10，11，12，13，14，15}处输入 。其余位置冻结为0 。内核并行应用于以下组ℓ = 4 bits。
与传统的极坐标编码相呼应，我们在树的每一层都迭代地遵循这一过程。在第二级，我们将Plotkin-4坐标应用于向量
以获得码字x。
在这项工作中，我们通过扩展核大小并将其参数化为神经网络，设计了极坐标编码和解码结构的非线性泛化。通过扩展设计空间以包括非线性和更大的内核，我们的目标是在神经Plotkin代码家族中发现更可靠的代码
图3。
（a）使用标准2×2内核的Polar（4,3）编码结构。编码在Plotkin树上递归执行。
（b）使用4×4核的Polar（16,8）编码。
（c）DEEPOLAR（4,3，ℓ=2）用神经网络代替Plotkin-2×2中的异或运算。
（d） DEEPPOLAR（16,8，ℓ=4）：将DEEPOLAR编码扩展到高阶内核使我们能够实现良好的可靠性。我们是第一个探索这个设计空间的人