在传染病传播的研究中,水传播途径是一个重要的考量因素。SEAIRW 模型(易感者 S - 暴露者 E - 感染者 I - 无症状感染者 A - 康复者 R - 水中病原体 W)综合考虑了人与人接触传播以及水传播的双重机制,为分析此类传染病提供了全面的框架。图中的微分方程组清晰地定义了各变量的动态变化:
\(\begin{cases} \frac{dS}{dt} = -\beta S (I + kA) - \beta_w S W \\ \frac{dE}{dt} = \beta S (I + kA) + \beta_w S W - p\omega' E - (1 - p)\omega E \\ \frac{dI}{dt} = (1 - p)\omega E - \gamma I \\ \frac{dA}{dt} = p\omega' E - \gamma' A \\ \frac{dR}{dt} = \gamma I + \gamma' A \\ \frac{dW}{dt} = \mu I + \mu' A - \epsilon W \end{cases}\)
一、模型方程深度解析
- 易感者 S:\(\frac{dS}{dt} = -\beta S (I + kA) - \beta_w S W\),表示易感者因接触感染者 I、无症状感染者 A(传播概率 k)以及水中病原体 W(传播系数 \(\beta_w\))而减少。
- 暴露者 E:\(\frac{dE}{dt} = \beta S (I + kA) + \beta_w S W - p\omega' E - (1 - p)\omega E\),包含感染输入(来自 S 的感染)、向无症状感染者(\(p\omega' E\))和感染者(\((1 - p)\omega E\))的转化。
- 感染者 I:\(\frac{dI}{dt} = (1 - p)\omega E - \gamma I\),由暴露者转化而来(\((1 - p)\omega E\)),并以速率 \(\gamma\) 康复。
- 无症状感染者 A:\(\frac{dA}{dt} = p\omega' E - \gamma' A\),由暴露者转化(\(p\omega' E\)),并以速率 \(\gamma'\) 康复。
- 康复者 R:\(\frac{dR}{dt} = \gamma I + \gamma' A\),汇总感染者和无症状感染者的康复贡献。
- 水中病原体 W:\(\frac{dW}{dt} = \mu I + \mu' A - \epsilon W\),包含感染者和无症状感染者向水中释放病原体(\(\mu I + \mu' A\)),以及病原体的自然去除(\(\epsilon W\))。
二、MATLAB 代码实现细节
1. 参数与初始条件设置
Matlab
md.b = 0.8; % 易感者与感染者接触率
md.bW = 0.5; % 易感者与水中病原体接触率
md.kappa = 0.05; % 无症状感染者向易感者传播的概率
md.p = 0.3; % 成为无症状感染者的概率
md.omega = 1; % 暴露者转为感染者的速率
md.omegap = 1; % 暴露者转为无症状感染者的速率
md.gamma = 1/3; % 感染者康复率
md.gammap = 0.03846; % 无症状感染者康复率
md.c = 0.48; % 无症状感染者向水中释放病原体的速率
md.epsilon = 0.1; % 水中病原体去除速率
t = 1:1:100; % 模拟100天
% 初始比例
s0 = 798/800;
i0 = 2/800;
e0 = i0 / ((1-md.p) * md.omega);
a0 = 0;
r0 = 0;
w0 = 0;
N0 = 800;
X0 = [s0, e0, i0, a0, r0, w0]; - 详细设定传播、转化、康复等速率参数,以及初始时刻各仓室的比例和水中病原体浓度。
2. 干预措施与模拟循环
Matlab
itimes = 4; % 增加感染者的时间点
iamounts = 6; % 增加的感染者数量
stimes = 5; % 增加易感者的时间点
samounts = 600; % 增加的易感者数量
for idx = 1:length(t)
currenttime = t(idx);
if currenttime == itimes
X0(3) = (X0(3)*N0 + iamounts)/N0; % 增加感染者比例
X0(1) = (X0(1)*N0 - iamounts)/N0; % 减少易感者比例
end
if currenttime == stimes
N0 = N0 + samounts; % 更新总人口
X0=X0.*((N0 - samounts)/N0); % 调整各仓室比例
X0(1) = X0(1) + samounts/N0; % 增加易感者比例
end
dXdt = SEAIRW_model(currenttime,X0, md);
X0 = X0 + dXdt';
% 保存结果...
end - 在特定时间点(第 4 天和第 5 天)实施干预,模拟现实中的疫情变化,如突发感染事件和人口流动。
3. 模型函数定义
Matlab
function dXdt = SEAIRW_model(t, X, md)
s = X(1); e = X(2); i = X(3); a = X(4); r = X(5); w = X(6);
dsdt = -md.b * s * (i + md.kappa * a) - md.bW * s * w;
dedt = -dsdt - (md.p * md.omegap + (1-md.p) * md.omega) * e;
didt = (1-md.p) * md.omega * e - md.gamma * i;
dadt = md.p * md.omegap * e - md.gammap * a;
drdt = md.gamma * i + md.gammap * a;
dwdt = (i + a * md.c) * md.epsilon - md.epsilon * w;
dXdt = [dsdt; dedt; didt; dadt; drdt; dwdt];
end - 严格按照模型方程计算各变量的导数,确保模拟的准确性。
三、结果可视化与分析
通过绘图展示各变量随时间的变化:
Matlab
figure;
plot(S, 'k-', 'LineWidth', 1.5); hold on;
plot(E, 'g-', 'LineWidth', 1.5);
plot(I, 'r-', 'LineWidth', 1.5);
plot(A, 'm-', 'LineWidth', 1.5);
plot(R, 'c-', 'LineWidth', 1.5);
plot(W, 'b-', 'LineWidth', 1.5);
legend('S', 'E', 'I', 'A', 'R', 'W','Location','east');
xlabel('Time(Day)');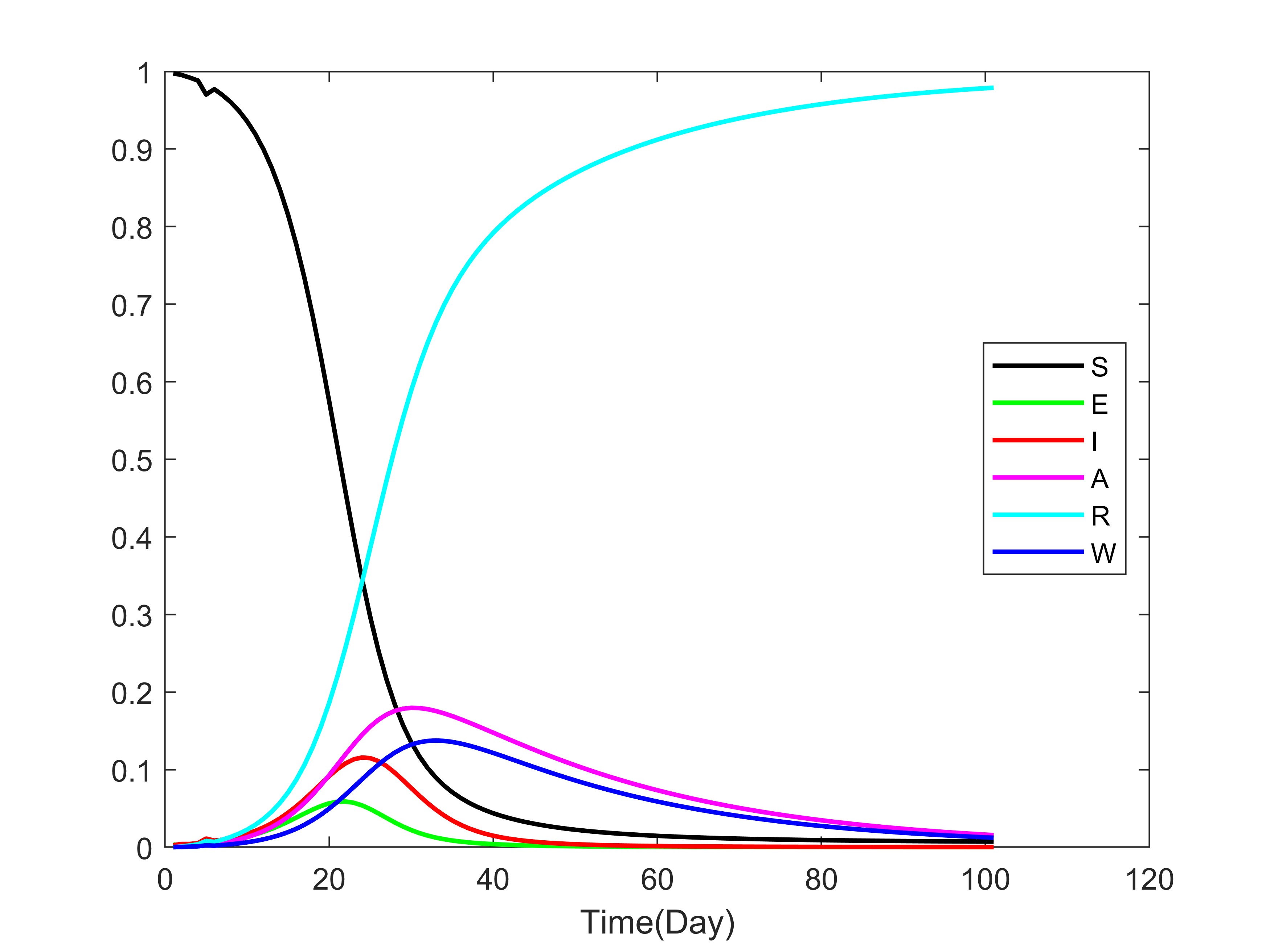
- 易感者 S 因感染逐渐减少,暴露者 E 先升后降,感染者 I 和无症状感染者 A 呈现动态变化,康复者 R 持续增加,水中病原体 W 随释放和去除机制波动。
四、模型应用与价值
SEAIRW 模型综合了接触传播和水传播途径,适用于霍乱、伤寒等水传播疾病的研究。通过 MATLAB 代码实现,能够模拟不同干预措施下的疫情发展,为公共卫生决策提供科学依据,如优化水源管理、制定隔离政策等。模型的灵活性和可扩展性使其成为分析复杂传染病传播的有力工具。
通过深入理解 SEAIRW 模型及其 MATLAB 实现,我们能够更有效地应对水传播传染病的挑战,为保障公众健康提供坚实的支持。快来尝试调整参数,探索不同场景下的疫情动态吧! 💻🦠
完整代码 (省流版)
Matlab
close all; clear; clc;
% # Initial parameter settings
md.b = 0.8; % Contact rate between susceptible and infected individuals
md.bW = 0.5; % Contact rate between susceptible and infected in water
md.kappa = 0.05; % The probability of transmission from asymptomatic to susceptible
md.p = 0.3; % The probability of being asymptomatic
md.omega = 1; % Transition rate from exposed to infectious
md.omegap = 1; % Transition rate from exposed to asymptomatic
md.gamma = 1/3; % Recovery rate of infectious individuals
md.gammap = 0.03846; % Recovery rate of asymptomatic individuals
md.c = 0.48; % The rate of pathogens shedding into water by asymptomatic individuals
md.epsilon = 0.1; % The rate of pathogen removal from water
t = 1:1:100; % Time from day 1 to day 100 (100 days in total)
% # Initialize variables
s0 = 798/800; Initial % proportion of susceptible individuals
i0 = 2/800; % Initial proportion of infectious individuals
e0 = i0 / ((1-md.p *) md.omega); % Initial proportion of exposed individuals
a0 = 0; % Initial proportion of asymptomatic individuals
r0 = 0; % Initial proportion of recovered individuals
w0 = 0; % Initial concentration of pathogens in water
N0 = 800; % Initial total population
% Initial state vector
X0 = [s0, e0, i0, a0, r0, w0];
%
% # Run SEAIRW model
% Pre-allocate result arrays
S = zeros(1, length(t)+ 1); % Array to store susceptible proportions
E = zeros(1, length(t)+ 1); % Array to store exposed proportions
I = zeros(1, length(t)+ 1); % Array to store infectious proportions
A = zeros(1, length(t)+ 1); % Array to store asymptomatic proportions
R = zeros(1, length(t)+ 1); % Array to store recovered proportions
W = zeros(1, length(t)+ 1); % Array to store pathogen concentrations in water
% Initialize the state at the first time point
S(1) = s0;
E(1) = e0;
I(1) = i0;
A(1) = a0;
R(1) = r0;
W(1) = w0;
% Define the time points and amounts for interventions
itimes = 4; % The time point (in days) to add infectious individuals
iamounts = 6; % The number of infectious individuals to add
stimes = 5; % The time point (in days) to add susceptible individuals
samounts = 600; % The number of susceptible individuals to add
% Main simulation loop
for idx = 1:length(t)
currenttime = t(idx);
% Handle intervention events
if currenttime == itimes
X0(3) = (X0(3)*N0 + iamounts)/N0; % Increase the number of infectious individuals
X0(1) = (X0(1)*N0 - iamou nts)/N0; % Decrease the number of susceptible individuals
end
if currenttime == stimes
N0 = N0 + samounts; % Update the total population
X0=X0.*((N0 - samounts)/N0); % Adjust the proportions of all compartments
X0(1) = X0(1) + samounts/N ;0 % Increase the proportion of susceptible individuals
end
% Calculate the derivatives at the current time point
dXdt = SEAIRW_model(currenttime,X0, md);
% Update the state variables
X0 = X0 + dXdt';
% Save the results
S(idx + 1) = X0(1);
E(idx + 1) = X0(2);
I(idx + 1) = X0(3);
A(idx + 1) = X0(4);
R(idx + 1) = X0(5);
W(idx + 1) = X0(6);
end
% # Plot results the
figure;
% Plot the curves of each variable
plot(S, 'k-', 'LineWidth', 1.5); % Black line for S
hold on;
plot( E, 'g-', 'LineWidth', 1.5); % Green line for E
plot( I, 'r-', 'LineWidth', 1.5); % Red line for I
plot( A, 'm-', 'LineWidth', 1.5); % Magenta line for A
plot( R, 'c-', 'LineWidth', .15); % Cyan line for R
plot( W, 'b-', 'LineWidth', 1.5); % Blue line for W
% Add legend
legend('S', 'E', 'I', 'A', 'R', 'W','Location','east');
xlabel('Time(Day)');
% Define the SEAIRW model function
function dXdt = SEAIRW_model(t, X, md)
s = X(1); % Proportion of susceptible individuals
e = X(2); % Proportion of exposed individuals
i = X(3); % Proportion of infectious individuals
a = X(4); % Proportion of asymptomatic individuals
r = X(5); % Proportion of recovered individuals
w = X(6); % Concentration of pathogens in water
% SEAIRW model equations
dsdt = -md.b * s * (i + md.kappa * a) - md.bW * s * w; % Change rate of susceptible individuals
dedt = -dsdt - (md.p * md.omegap + (1-md.p) * md.omega) * e; % Change rate of exposed individuals
didt = (1-md.p) * md.omega * e - md.gamma * i; % Change rate of infectious individuals
dadt = md.p * md.omegap * e - md.gammap * a; % Change rate of asymptomatic individuals
drdt = md.gamma * i + md.gammap * a; % Change rate of recovered individuals
dwdt = (i + a * md.c) * md.epsilon - md.epsilon * w; % Change rate of pathogens in water
dXdt = [dsdt; dedt; didt; dadt; drdt; dwdt]; % Combine all derivatives into a vector
end