

文章目录
本节非常重要
初等变换
初等变换使用"→",而不是"="
初等行变换
① 交换两行

② 非0数乘以某一行

③ 某一行的L倍加到另一行上去

初等列变换
列与行同理
矩阵的标准型
从左上角开始,一串1,其余地方全是0,这个就叫标准型


阶梯形与行最简阶梯形
阶梯型矩阵
- 如有0行,0行在非0行的下面
- 非0行的首非0元的左下方的元素 (若有的话) 全是0


要点:竖线只过一个数,横线可以跨多个数
行简化阶梯形
- 必须是阶梯形
- 非0行的首非0元是1
- 非0行的首非0元的所在列其他元素是0

定理: 任何的矩阵A都可以经过初等变换,化成一个阶梯形

初等矩阵
定义
由单位E做一次初等变换(行、列)得到的矩阵就叫做初等矩阵
第一种:
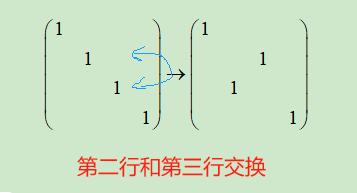

第二种:


第三种:

第j行的L倍加到第i行上去
第i列的L倍加到第j行上去

性质
-
初等矩阵的行列式不为0

-
初等矩阵的转置矩阵仍是同类型初等矩阵


-
初等矩阵均可逆,其逆矩阵也是同种类型的初等矩阵

初等矩阵和初等变换的联系
- A做一次初等行 变换,相当于用同种的初等矩阵去左乘A

- A做一次初等列 变换,相当于用同种的初等矩阵去右乘A

观看笔记来源: 《线性代数》教学视频 宋浩老师(2024年更新)