1. 哈希:

之前我们的红黑数的查找是由于左边小右边大的原则可以快速的查找,我们这里的哈希表呢?
这里是用过哈希函数把关键字key和存储位置建立一个关联的映射。
直接定址法(函数函数定义的其中一种):
直接定址法是我们设置哈希函数的第一种方法:

直接定址法的限制就是适用范围比较集中的时候,如果范围不集中的话,我们就不能使用直接定址法。
负载因子:

负载因子其实表示的哈希表的空间的利用率,负载因子越大的时候,空间利用率就越大,哈希冲突的概率就越大,负载因子越小的时候,空间利用率越小,哈希冲突的概率就越小。
要注意这里是概率,不是一定的冲突就大或者小,有可能这批数据刚好比较合适就没有啥冲突。
哈希冲突:

直接定址法是不会有哈希冲突的,直接定址法适用于数据范围比较集中,直接定址法是会给每个值都分配一个空间的。所以不会有哈希冲突。
但是直接定址法的话,我们当然不能一直使用这个,当我们的其他的环境下,我们的数据并不集中的话,我们其实常常使用的是其他的构建哈希函数的方法,他可能会导致几个数据映射到同一个位置上去,导致哈希冲突。
哈希函数:

我们接下来看定义我们的哈希函数的方法:
除法散列法/除留余数法:

除留余数法,我们要让所有的值都映射到M个空间里面,M是哈希表的大小,我们就让关键值key取模M,那么他取模得到的值一定是M-1这个范围里面的某一个,这就映射出了一个位置。
我们看上面的图片,我们看第二点,他说我们的哈希表的大小M要尽量避免2的幂和10的幂。因为我们要计算数据映射的位置的时候,我们是要使用数据来除以哈希表的大小M来得到的。如果使用他们的话就会导致冲突比较大。
除留余数法的话就比直接定址法好多了,我们不需要管数据的范围的大小,我们只要开比数据个数要大的空间就可以。

这就是除留余数法(M是哈希表的大小),19%M得到8,19就映射到8这个位置,然后其他的数据也是一样的,取模M得到一个映射的位置,但是我们的看到30取模M的结果得到的也是8,这个就是我们的哈希冲突。
哈希冲突是不可避免的,我们接下来要讲解如果处理哈希冲突;
我们还有其他的构建哈希函数的方法,乘法散列法和全域散列法,这两个的话我们知道了解一下就行,不进行细讲。
处理哈希冲突:


开放定址法:
当⼀个关键字key⽤哈希函数计算出的位置冲突了,则按照某种规则找到⼀个没有存储数据的位置进⾏存储。简单的说就是我们的这个数据映射出的位置被别人占了,我们就找一个新的位置占上。
这个找新位置的规则我们分成三种:线性探测,二次探测,双重探测。
我们主要学的是线性探测。 
线性探测就是映射到这个位置但是这个位置被占了,我们就从这个发生冲突的位置开始,我们就依次的往后走,直到遇到一个空的位置,我们就占到这个位置上(如果走到哈希表的尾了,我们就绕到头上去)。
当我们的映射的这个位置发生冲突被别的数据占据了之后,我们的公式就是给哈希这个位置+1然后继续取模往后走, 走到哈希表的尾了,但是我们是取模进行移动的,比如图中的,hash0+i从10变成11的时候,他取模的到的结果就可以跳转回到头部。
开放定址法代码实现:
insert():


Find():

Erase():

素数表:
我们之前说我们要使用素数来设置哈希表的大小,但是如果这个哈希表满了以后,我们需要扩容的时候,我们一般都会给这个哈希表*2来进行扩容,这时候的到的就不是一个素数,可能会导致哈希冲突变大。
我们的库里面就给出了一个不太接近2的素数表。

你看下面的那个是一个lower_bound的函数,这个就是找大于等于的,我们在下面的扩容里面实现的话,我们就可以调用这个素数表的函数,他每次扩容的话,就走到了下一个素数的位置。

当前的size()+1的话,里面的lower_bound是会给你找比这个大或者相等的数据的,假如现在的size()是53,你给他+1,得到54,那么他就会找比54大的数据来进行的。
key不能取模的问题:
我们这里还有一个问题那就是key如果不是我们的int类型的时候,我们建立哈希函数的话,我们是必须要使用除留余数法的,但是如果key不是int类型的,那怎么取模呢?

我们看这个函数,他是绝对插入不到我们的哈希表里面去的,我们的insert函数,我们是要使用到dict.first进行判断的。(这里编译就会报错);
那我们这里怎么解决呢?
我们这里就要走两层映射,首先把string映射成int类型的,然后把int映射到哈希表的位置上。
那怎么把string类型的映射成int类型的数据呢?我们可以把string里面的每一个字母的ASCII值加起来,这个逻辑还比较合适。

那实现怎么来实现呢?
我们就实现一个仿函数来进行我们的转化,
我们先看下面的这个图片:
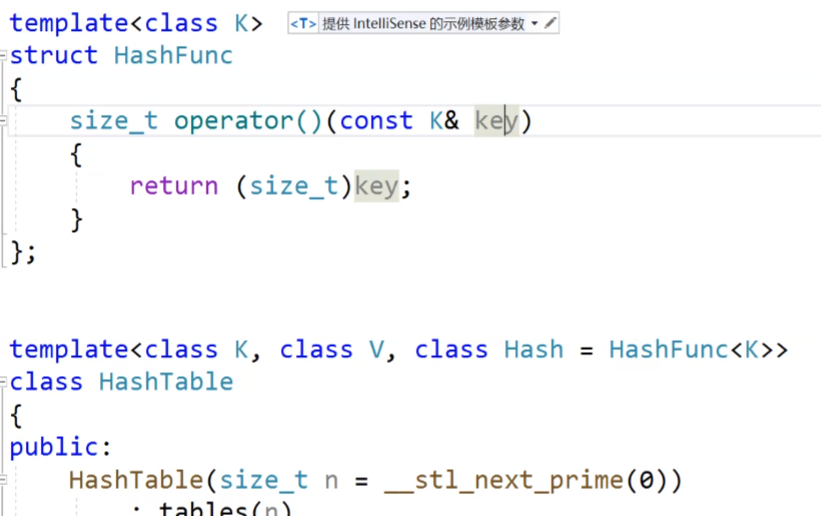
我们给我们的模板的第三个参数是我们的Hash仿函数,我们给他传一个默认的缺省函数HashFunc函数,这个函数的话,我们会把传进来的类型转为size_t类型的数据,但是有的类型他是转换不成size_t类型的数据的,这时候我们就要自己来手动的实现一个仿函数来进行转换。

这个就是我们实现的仿函数,我们把这个仿函数传进去。



还记得我们之前的仿函数是怎样使用的呢?
我们的仿函数实例化出的对象我们可以直接当作函数来进行使用,看上面Hash仿函数实例化对象hs以后,hs(key)这个就是直接调用仿函数,把key数据转换成int类型的可以取模的数据。
这时候看我们的pair键值对的类型是string类型的,这个类型转成int类型的话,我们就要传我们的自己的仿函数进去才行。

你传其他类型的key也能用,但是的话,你要配一个仿函数类帮助他可以进行取模(必须要能取模,这是构建哈希函数的必要途径)。
我们继续往下看:

我们看,我们刚才自己实现的string转换为int的仿函数,我们是让所有的字母的ASCII加起来,但是这样的话,我们看上面的图片,这三个string的顺序不一样,但是他们的ASCII是一样的,最后导致他们映射的int是同一个,这就导致了冲突,那我们的这个仿函数是不是就显得没有那么好呢?
那有没有刚好的方法来实现这个仿函数,有的,有人提出了BKDRHash方法来进行:

这样我们加起来的ASCII相同的不同顺序的字符串,除非是这两个ASCII值相等的字符串顺序都一样,不然最后计算得到的结果不可能一样。
我们继续往下看:

当我们的容器是我们的unordered_map,这个容器的底层是哈希表实现的,我们给他的key传上string的时候,它不需要仿函数就可以通过运行,但是我们的HashTables我们就要加上仿函数才可以。
要知道我们的string是要经常使用的,经常使用的话,我们想办法让key默认的支持string转化,我们可以使用一个特化来实现。

这个就是特化的实现,当我们的key是string类型的时候,他就是走特化,就不需要仿函数,我们的unordered_map使用的是库里面的,他的底层是由哈希表封装的,库里面已经把这个string的特化实现过了,我们这里调用unordered_map给key传string的话,他就不需要仿函数。
但是我们的这里的哈希表是我们自己在进行实现,我们没有实现特化,我们就要仿函数。
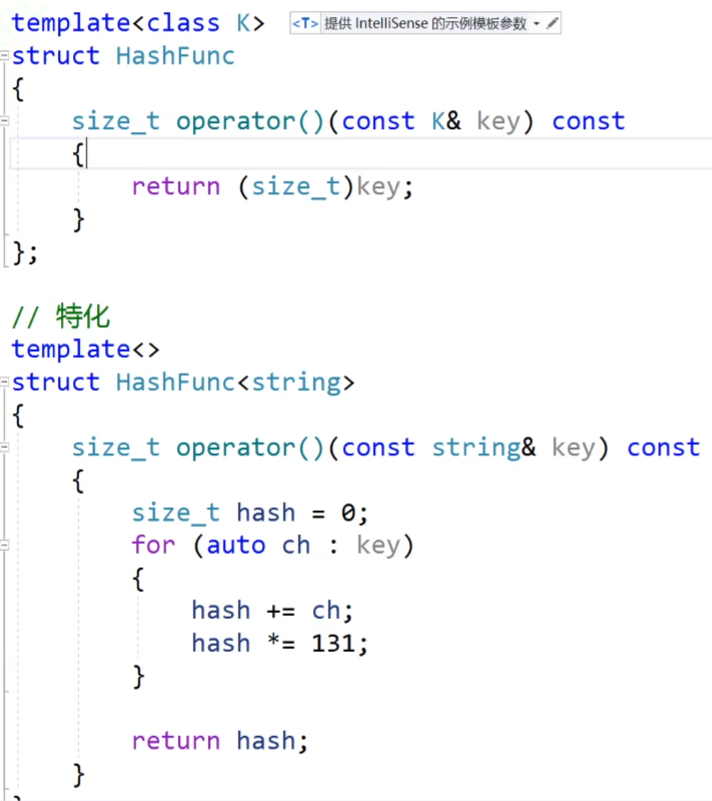
我们看这个特化,特化的上面是我们的仿函数,我们的哈希表可以传各种类型的数据进来,然后我们传仿函数,把各种类型转换为size_t类型的。也可以不传仿函数,把string的特化出来,我们传string类型的数据进来后就直接调用特化的模板了。

现在我们这样就没事,就可以了,我们已经特化了string类型的数据,可以不传仿函数。
我们继续往下看:
我们看这个:

当我们的调用库里面的unordered_map的时候,我们传K传pair<>键值对,这时候也是有问题的,库里面没有实现pair<>键值对的特化,如果想要这种的话,还是需要你手动的实现仿函数。

看这个特化,为了防止你1,3和3,1算出来的值是一样的,减少哈希冲突的发生,使用BKDRHash来实现。

然后接着我们传仿函数进去,然后我们的键值对存1,3和3,1两个数据,实现哈希表的话,这两个数据分别进行存储,我们当然不想让他产生哈希冲突,我们上面的仿函数就使用BKDRHash来实现。
我们看我们的f第二种解决哈希冲突的方法:
链地址法:
这个叫作拉链法,链地址法,这个是非常重要的解决哈希冲突的方法。
