最小二乘法拟合直线，用线性回归法、梯度下降法实现

参考笔记：

[2.1 模型假设](#2.1 模型假设)

[2.2 定义误差函数](#2.2 定义误差函数)

[2.3 求偏导并解方程](#2.3 求偏导并解方程)

[2.4 案例实例](#2.4 案例实例)

[2.4.1 手工计算实例](#2.4.1 手工计算实例)

[2.4.2 使用Python实现](#2.4.2 使用Python实现)

3.梯度下降法

[3.1 前言（梯度下降算法原理介绍）](#3.1 前言（梯度下降算法原理介绍）)

[3.2 模型假设](#3.2 模型假设)

[3.3 定义损失函数](#3.3 定义损失函数)

[3.4 梯度计算](#3.4 梯度计算)

[3.5 更新参数](#3.5 更新参数)

[3.6 代码演示](#3.6 代码演示)

4.其他方法

1.问题引入

在数据分析问题中，常常需要通过 n 组二维数据点拟合出一条直线，其中斜率 a、截距 b 是未知参数，如下图所示：

那为什么要说拟合呢？这是因为我们无法找到一条直线经过所有的点，也就是说方程无确定解

于是这就是我们引出了要解决的问题：虽然没有确定解，但是我们能不能求出近似解，即拟合出一条直线，使得这条直线能最佳地反映数据点的整体趋势

那么问题又来了， "最佳的准则" 是什么呢？可以是所有数据点到直线的距离总和最小 ，也可以是所有数据点到直线的误差（真实y值 - 拟合y值）绝对值总和最小，也可以是其他。如果是你面临这个问题你会怎么选择？

早在 19 世纪，勒让德就认为让 **"误差的平方和最小"**拟合出来的直线是最接近真实情形的

为什么是 "误差的平方和" 而不是其它的，这个问题连欧拉、拉普拉斯都未能成功回答，后来是高斯建立了一套误差分析理论，从而证明了确实是使 "误差的平方和最小" 的情况下系统是最优的。这个我们就无需深究了

按照勒让德的 "误差的平方和最小" 最佳原则，于是就是求：

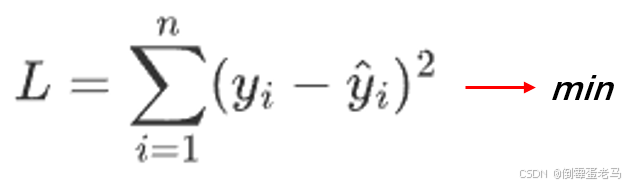
：真实 y 值：拟合 y 值

拟合一条直线，其实就是找最优斜率 a 、最优截距 b 的过程，所以我们可以通过上面的 L 函数，在其取得最小值 min 时得到的 a、b 即为最优解，这样拟合出了 n 组数据点的最佳直线

这就是最小二乘法的思想，所谓 "二乘" 就是平方的意思

至于怎么求出具体的 a、b，理论上可以用：

① 线性回归法

② 梯度下降法：就是模型训练，把 L 作为损失函数即可

③ .....

下面我们就以最常用的线性回归、梯度下降法为例进行推导和求解

2.线性回归法

线性回归法也称为直接法，计算简单，可以直接推导出拟合直线的，而且许多非线性的问题也可以转化为线性问题来解决，所以得到了广泛的应用

2.1 模型假设

假设我们有 n 组二维数据点，我们的目标是找到一条直线，其中 a 为直线斜率，b为截距，使得这条直线尽可能接近所有数据点

2.2 定义误差函数

对于每个数据点，预测值为，则误差为：

**目标：**最小化所有数据点的误差平方和：

最终目标就是找到使总误差 S 最小的 a、b，这可以通过 S 分别对 a、b 求偏导，并令偏导数 = 0 来实现

2.3 求偏导并解方程

为了找到使总误差 S 最小的 a、b，可以对 a 和 b 分别求偏导，令导数为 0 ，得到方程组如下：

整理后得到如下方程：

注：

通过代数运算消元，解得：

🆗，这样就能拟合出有 n 组二维数据点的一条直线。可以看到，整个过程非常简单，只需要数学计算即可

2.4 案例演示

2.4.1 手工计算实例

假设有以下数据点：

计算中间项：

代入公式：

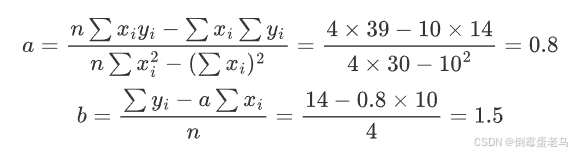
拟合直线：

2.4.2 使用Python实现

我们将 2.4.1 中的手工计算例子使用 Python 来实现，并作可视化

python 复制代码

import numpy as np
import matplotlib.pyplot as plt

plt.rcParams["font.sans-serif"] = ["SimHei"]  #设置字体，可以显示中文
plt.rcParams["axes.unicode_minus"] = False  # 正常显示负号

# 1. 生成数据
x = np.array([1, 2, 3, 4])
y = np.array([2, 3, 5, 4])

# 2. 最小二乘法实现
def linear_regression(x, y):
    """
    最小二乘法线性回归
    参数:
        x: 数据点的x坐标值
        y: 数据点的y坐标值
    返回:
        (a, b): 斜率，截距
    """
    n = len(x)
    sum_x = np.sum(x)
    sum_y = np.sum(y)
    sum_x2 = np.sum(x ** 2)
    sum_xy = np.sum(x * y)

    # 计算斜率
    a = (n * sum_xy - sum_x * sum_y) / (n * sum_x2 - sum_x ** 2)
    b = (sum_y - a * sum_x) / n

    return (a, b)

#执行回归计算，a：拟合出来的斜率 b：拟合出来的截距
a, b = linear_regression(x, y)

# 3. 可视化结果
plt.figure(figsize=(10, 6), dpi=100)

#绘制数据点
plt.scatter(x, y,
            color='steelblue',  # 点颜色
            s=90,  # 点大小
            edgecolor='white',  # 边缘颜色
            linewidth=1.5,  # 边缘线宽
            label='数据点',
            zorder=1)  # 绘制层级


#绘制拟合直线
x_fit = np.array([min(x) - 1, max(x) + 1])  # 延长拟合线范围
y_fit = a * x_fit + b
plt.plot(x_fit, y_fit,
         color='crimson',
         linewidth=3,
         label=f'拟合结果 ($y={a:.2f}x + {b:.2f}$)',
         zorder=1)

#添加图表元素
plt.title('最小二乘法线性回归演示', fontsize=14, pad=20)
plt.xlabel("X 值", fontsize=12)
plt.ylabel("Y 值", fontsize=12)
plt.grid(True, linestyle='--', alpha=0.7)
plt.legend(fontsize=12, frameon=True, shadow=True)

# 设置坐标轴范围
plt.xlim(min(x) - 1, max(x) + 1)
plt.ylim(min(y) - 2, max(y) + 2)

# 显示图表
plt.tight_layout()
plt.show()

运行结果：

3.梯度下降法

3.1 前言（梯度下降算法原理介绍）

梯度下降（Gradient Descent）是一种迭代优化算法，通过不断沿损失函数负梯度方向更新参数，逐步逼近最优解。对于线性回归问题，需最小化均方误差（MSE）：

其中为斜率，为截距

3.2 模型假设

假设我们有 n 组二维数据点，我们的目标是找到一条直线，其中 a 为直线斜率，b 为截距，使得这条直线尽可能接近所有数据点

3.3 定义损失函数

对于每个数据点，我们希望拟合的直线为
定义预测值 为：
定义平方误差项 为：
总的误差平方和（损失函数）为：

3.4 梯度计算

为了使用梯度下降法，需要计算损失函数对参数a和b的偏导数（梯度）:

对 a 的偏导数：

对 b 的偏导数：

3.5 更新参数

通过梯度下降法，我们可以更新参数 a、b，使其朝着减少损失函数的方向移动。更新规则为：

其中为学习率，控制更新步长

重复计算梯度并更新参数，直到达到预设的迭代次数或损失函数的变化小于某个阈值

理论上，随着迭代次数的增加，损失函数会逐渐减小，最终收敛到损失函数的局部最小值，得到最佳的斜率 a、截距 b

🆗，以上就是梯度下降法的整个流程，下来我们会用 Python 举一个案例并作可视化

3.6 代码演示

python 复制代码

import numpy as np
import matplotlib.pyplot as plt

plt.rcParams["font.sans-serif"] = ["SimHei"]  #设置字体，可以显示中文
plt.rcParams["axes.unicode_minus"] = False  # 正常显示负号

# 固定随机种子保证可重复性
np.random.seed(42)

# 生成模拟数据
# 生成100个[0-10]区间均匀分布的值，作为数据点的x坐标值
x = np.linspace(0, 10, 100)

# 生成理想的线性关系： y = 2.5x + 1.8
true_a = 2.5  #真实斜率
true_b = 1.8  #真实截距
y = true_a * x + true_b

# 添加高斯噪声来模拟真实数据
noise = np.random.normal(0,2,size=len(x))
y = y + noise #作为数据点的y坐标点

# 梯度下降参数
alpha = 0.01  # 学习率
iterations = 2000  # 迭代次数

# 参数初始化
a, b = 0.0, 0.0
n = len(x)

# 记录训练过程
history = {'a': [], 'b': [], 'loss': []}

# 梯度下降迭代
for i in range(iterations):
    # 预测值
    y_pred = a * x + b

    # 计算梯度
    grad_a = (-2 / n) * np.sum(x * (y - y_pred))
    grad_b = (-2 / n) * np.sum(y - y_pred)

    # 更新参数
    a -= alpha * grad_a
    b -= alpha * grad_b

    # 记录损失值loss、参数a、参数b
    loss = (1/n) * np.sum((y - y_pred) ** 2)
    history['a'].append(a)
    history['b'].append(b)
    history['loss'].append(loss)

# 最终结果
print(f"真实参数: a={true_a}, b={true_b}")
print(f"拟合结果: a={a:.2f}, b={b:.2f}")

# 可视化
plt.figure(figsize=(12, 4))

# 损失函数下降曲线
plt.subplot(131)
plt.plot(history['loss'], color='darkorange')
plt.xlabel('Iteration')
plt.ylabel('Loss')
plt.title('Loss Function Convergence(损失函数下降曲线)')

# 参数变化轨迹
plt.subplot(132)
plt.plot(history['a'], history['b'], marker='o', markersize=2)
plt.xlabel('a')
plt.ylabel('b')
plt.title('Parameter Trajectory(参数变化轨迹)')

# 最终拟合效果
plt.subplot(133)
plt.scatter(x, y, alpha=0.6, label='数据点')
plt.xlabel('X')
plt.ylabel('Y')
plt.plot(x, a * x + b, color='crimson', lw=3,
         label=f'拟合结果: y={a:.2f}x + {b:.2f}')
plt.plot(x, true_a * x + true_b, 'k--', label=f'True: y={true_a:.2f}x + {true_b:.2f}')
plt.title('最小二乘法梯度下降演示')

plt.legend()
plt.tight_layout()
plt.show()

运行结果：

可以看到，经过 2000 次的迭代，最终的拟合结果是，非常接近 True

🆗，以上就是本文最小二乘法拟合直线的所有内容，后续如果学习到其他方法还会继续更新，整个流程走下来感觉还是挺有趣的

4.其他方法

待更新....