- 二分查找
- 在排序数组中查找元素的第一个和最后一个位置
- 搜索插入位置
- [x 的平方根](#x 的平方根)
二分查找
题目描述
给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果 target 存在返回下标,否则返回 -1。
你必须编写一个具有== O(log n)== 时间复杂度的算法。
示例 1:
输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4
示例 2:
输入: nums = [-1,0,3,5,9,12], target = 2
输出: -1
解释: 2 不存在 nums 中因此返回 -1
提示:
- 你可以假设 nums 中的所有元素是不重复的。
- n 将在 [1, 10000]之间。
- nums 的每个元素都将在 [-9999, 9999]之间。
算法原理
- 算法一:枚举法
扫描遍历一遍,时间复杂度自然为O(n).
- 算法二:二分查找:
二分查找作为一款经久不衰的算法自然有其魅力所在。
我们以输入: nums = [-1,0,3,5,9,12], target = 9为例
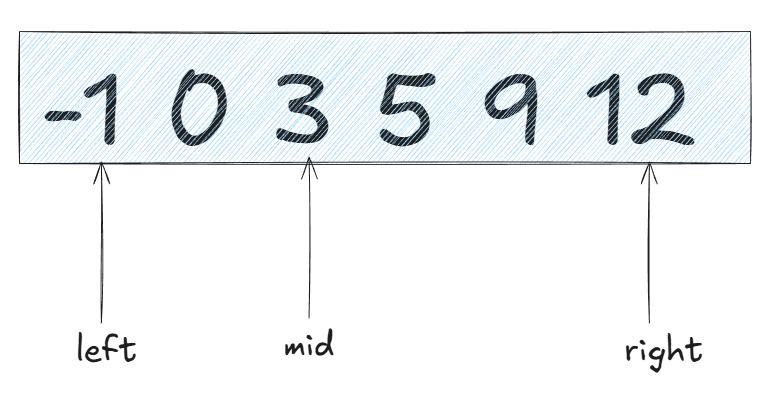
可以看到mid指针指向的数小于target,根据单调性。mid本身和mid左边的数都是小于target的,因此可以排除:
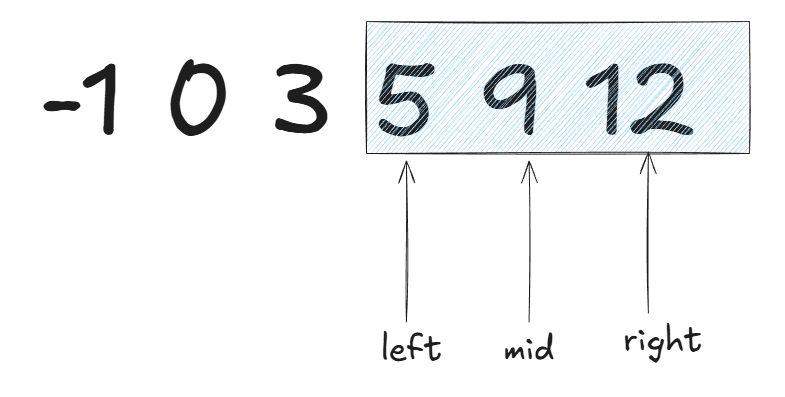
于是下次查找就出答案了。
可以看到我们二分查找一次干掉一半搜索区间,因此时间复杂度为O(logn).
实际上我们可以证明二分的时候,平均操作次数是最低的:
我们不妨设target等可能出现在每个数上,即每个数是target的可能为1/n.
我们使用k分查找,即将数组分成k叉树。树高为[logkn].
第i层的结点数量为ki.
因此查找次数期望为
1 n ∑ i = 0 l o g k n ( i + 1 ) k i \frac{1}{n}\sum_{i=0}^{log_kn}(i+1)k^i n1i=0∑logkn(i+1)ki
然后经过化简可以得到,k取2的时候得最小值。
算法实现
cpp
class Solution {
public:
int search(vector<int>& nums, int target)
{
int left = 0, right = nums.size() - 1, mid = 0;
while (left <= right)
{
mid = left + (right - left) / 2;
if (nums[mid] == target)
return mid;
else if (nums[mid] < target)
left = mid + 1;
else
right = mid - 1;
}
return -1;
}
};
在排序数组中查找元素的第一个和最后一个位置
题目描述
给你一个按照非递减顺序排列的整数数组 nums,和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。
如果数组中不存在目标值 target,返回 [-1, -1]。
你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。
示例 1:
输入:nums = [5,7,7,8,8,10], target = 8
输出:[3,4]
示例 2:
输入:nums = [5,7,7,8,8,10], target = 6
输出:[-1,-1]
示例 3:
输入:nums = [], target = 0
输出:[-1,-1]
提示:
- 0 <= nums.length <= 105
- -109 <= nums[i] <= 109
- nums 是一个非递减数组
- -109 <= target <= 109
算法原理
- 二分查找
既然要求O(logn)的时间复杂度那么就不能用枚举法了。我们直接用二分查找来做。
我们可以将排序数组看成三个区间:

那么我们现在相当于求绿色区间的左端点和右端点,这需要分开讨论。
先来看左端点:
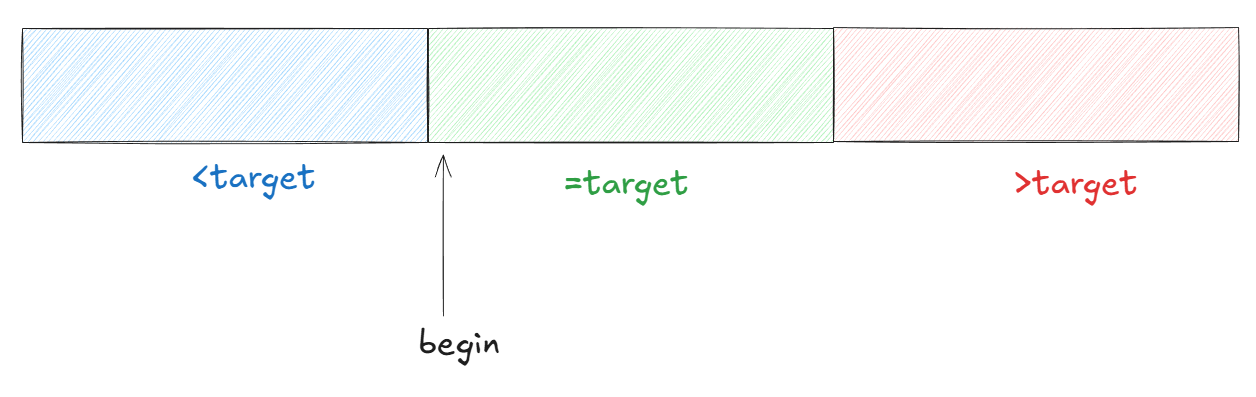
可以看到我们左端点可以将数组划分成两个区间,左边是<target,右边是>=target。其中我们的begin是右边区间的元素。
因此当我们的mid指向左区间元素时,mid势必不是最终结果。因此令left=mid+1.
但是当mid指向右区间元素时,mid可能是最终结果 ,因此需要保留令right=mid。
这时候也意味着我们取中点mid=left+(right-left)/2,必须向下取整。
这是个相当显然的事实。例如区间为[1,3]target=3.如果采取向上取整的算法求中点,我们可以算得mid=1.于是right和left不变。继续求的mid=1.就进入了死循环。
接下来看求右端点:
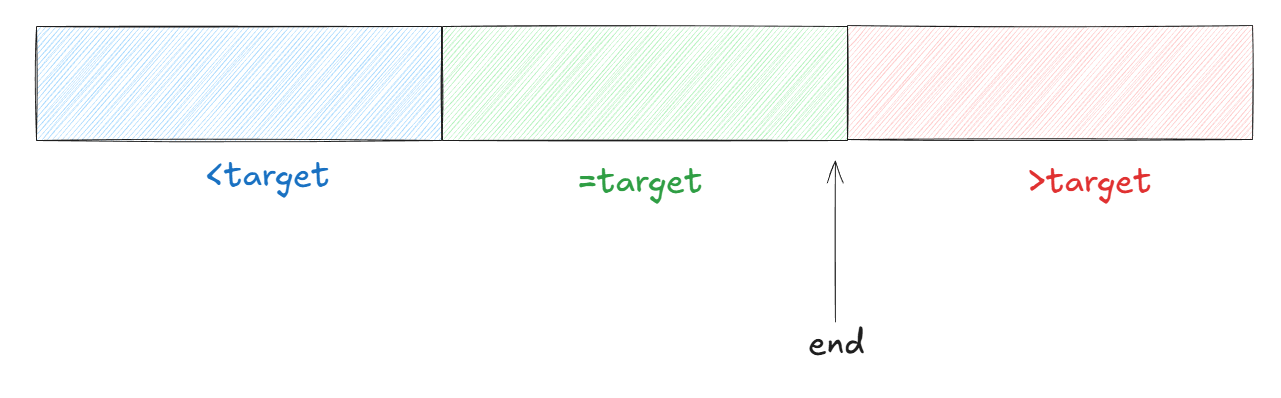
同样的我们的右端点把区间分成<=target和>target.
当mid落在左区间时有可能是最终结果,因此left=mid。
当mid落在右区间时,势必不可能为最终结果,因此right=mid-1.
这时候我们自然要采取向上取整的方式求中点,理由同上。
- 简而言之,当左区间有可能是最终结果时,我们要确保取中点时有向右区间的趋势,因此向上取整;当右区间有可能是最终结果时,我们要确保取中点时有向左区间的趋势,因此向下取整。
算法实现
cpp
class Solution {
public:
vector<int> searchRange(vector<int>& nums, int target)
{
//处理边界
if (!nums.size())
return { -1,-1 };
int left = 0, right = nums.size() - 1, begin = 0, mid = 0;
//找左边界
while (left < right)
{
mid = left + (right - left) / 2;
if (nums[mid] < target)
left = mid + 1;
else
right = mid;
}
if (nums[right] != target)
return { -1,-1 };
begin = left;
left = 0;
right = nums.size() - 1;
//找右边界
while(left<right)
{
mid = left + (right - left + 1) / 2;
if (nums[mid] > target)
right = mid - 1;
else
left = mid;
}
return { begin,right };
}
};
搜索插入位置
题目描述
给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。
请必须使用时间复杂度为 O(log n) 的算法。
示例 1:
输入: nums = [1,3,5,6], target = 5
输出: 2
示例 2:
输入: nums = [1,3,5,6], target = 2
输出: 1
示例 3:
输入: nums = [1,3,5,6], target = 7
输出: 4
提示:
- 1 <= nums.length <= 104
- -104 <= nums[i] <= 104
- nums 为 无重复元素 的 升序 排列数组
- -104 <= target <= 104
算法原理
- 二分查找
根据题目,我们知道我们要找的是第一个>=target的元素的位置。
即将数组化成成<target和>=target的两个区间,而我们要求右区间的左端点。参考上一题的求左端点算法即可.
算法实现
cpp
class Solution {
public:
int searchInsert(vector<int>& nums, int target)
{
if (target > nums.back())
return nums.size();
int left = 0, right = nums.size() - 1, mid = 0;
while (left < right)
{
mid = left + (right - left) / 2;
if (nums[mid] >= target)
right = mid;
else
left = mid + 1;
}
return right;
}
};
x 的平方根
题目描述
给你一个非负整数 x ,计算并返回 x 的 算术平方根 。
由于返回类型是整数,结果只保留 整数部分 ,小数部分将被 舍去 。
注意:不允许使用任何内置指数函数和算符,例如 pow(x, 0.5) 或者 x ** 0.5 。
示例 1:
输入:x = 4
输出:2
示例 2:
输入:x = 8
输出:2
解释:8 的算术平方根是 2.82842..., 由于返回类型是整数,小数部分将被舍去。
提示:
- 0 <= x <= 231 - 1
算法原理
- 算法一:枚举法
自1开始枚举各种可能,时间复杂度为O(n)
- 算法二:二分查找
输入x,相当于我们在[1,x]区间中找到一个最大的数pow使得pow*pow<=x.
即我们可以将[1,x]划分成两个区间:pow*pow<=x和pow*pow>x。
而我们要找的就是左区间的右端点。参考上上一题算法即可。
算法实现
cpp
class Solution {
public:
int mySqrt(int x)
{
int left = 0, right = x, mid = 0;
while (left < right)
{
mid = left + (right - left) / 2 + (right - left) % 2;
if (mid <= x/mid)
left = mid;
else
right = mid - 1;
}
return left;
}
};