使用libdivide加速整数除法运算

在x86和ARM平台上，整数除法是相对较慢的操作。不巧的是除法在日常开发中使用频率并不低，而且还有一些其他常用的运算依赖于除法操作，比如取模。因此频繁的除法操作很容易成为程序的性能瓶颈，尤其是在一些数值计算程序里。

人们当然也想了很多办法优化，比如在除数是2的幂的时候，除法可以用速度更快的位运算来替换。比较新的编译器都会自动进行这类优化。然而不是所有的除数都是2的幂，也不是所有表达式里的除数在编译期间可知，因此我们还需要一些别的手段。

libdivide就是这样一种整数除法的优化手段，它不仅能应用前面提到的位运算优化，它还可以在运行时根据除数和被除数的特性选择速度最快的算法来模拟除法操作，最有意义的地方在于如果硬件平台支持SIMD指令，它还会在条件允许下尽量使用SSE2/AVX2/AVX256/NEON等SIMD指令做优化，重复发挥了现代cpu的性能优势。按照项目文档的说法，在有SIMD的加持下，64位整数的除法运算最大可以提升10倍。

libdivide是个头文件库，这意味着只需要简单包含一下它提供的头文件就可以使用了，不需要额外的编译和安装。同时它的使用方法也很简单，库做了运算符重载，只要初始化一下它需要的对象就可以了：

c++ 复制代码

int64_t a = 1000;
libdivide::divider<int64_t> fast_d(10);
int64_t result = a / fast_d;
a /= fast_d;

c语言没有提供运算符重载的功能，因此得用libdivide_s64_gen等包装函数来完成相同的操作。

简单来说它几乎可以平替项目中的除法运算，不过在这之前我们得先检验下它承诺的性能提升是不是确有其事。

libdivide在测试用例里自带了一个性能测试程序，但这个程序的输出比较抽象，测试的场景也不够全面，因此我重新写了三个场景的场景做测试。

三个场景分别是除数未知、除数已知但是2的幂以及除数已知但不是2的幂。覆盖的情况是编译器做不了优化、编译器可以优化成位运算以及编译器能优化但不能直接用位运算进行替换这三种。

由于c++的编译期计算太强大，为了避免编译期计算搅局影响结果，测试数据中的大部分都是随机生成的，理论上性能测试中应该尽量减少这种随机生成的数据，但这里我们别无他法，而且说到底也是"评估"一下库的大致性能，不需要那么精确。测试用例不长，因此我就全搬上来了：

c++ 复制代码

// 场景1，除数未知，为了模拟除数未知所以除数也用了随机数
void bench_div(benchmark::State &stat)
{
    std::random_device rd;
    std::mt19937 gen(rd());
    std::uniform_int_distribution<int64_t> dis(1, 114515);
    std::vector<int64_t> v;
    for (int i = 0; i < 10; ++i) {
	    v.push_back(dis(gen));
    }
    int64_t d = dis(gen);
    for (auto _ : stat) {
	    for (auto n : v) {
            benchmark::DoNotOptimize(n/=d);
	    }
    }
}
BENCHMARK(bench_div);

void bench_libdiv(benchmark::State &stat)
{
    std::random_device rd;
    std::mt19937 gen(rd());
    std::uniform_int_distribution<int64_t> dis(1, 114515);
    std::vector<int64_t> v;
    for (int i = 0; i < 10; ++i) {
	    v.push_back(dis(gen));
    }
    libdivide::divider<int64_t> fast_d(dis(gen));
    for (auto _ : stat) {
	    for (auto n : v) {
            benchmark::DoNotOptimize(n/=fast_d);
	    }
    }
}
BENCHMARK(bench_libdiv);

// 场景2，除数的4，2的2次幂
void bench_div4(benchmark::State &stat)
{
    std::random_device rd;
    std::mt19937 gen(rd());
    std::uniform_int_distribution<uint64_t> dis(1, 114515);
    std::vector<uint64_t> v;
    for (int i = 0; i < 10; ++i) {
	    v.push_back(dis(gen));
    }
    uint64_t d = 4;
    for (auto _ : stat) {
	    for (auto n : v) {
            benchmark::DoNotOptimize(n>>=d);
	    }
    }
}
BENCHMARK(bench_div4);

void bench_libdiv4(benchmark::State &stat)
{
    std::random_device rd;
    std::mt19937 gen(rd());
    std::uniform_int_distribution<uint64_t> dis(1, 114515);
    std::vector<uint64_t> v;
    for (int i = 0; i < 10; ++i) {
	    v.push_back(dis(gen));
    }
    uint64_t d = 4;
    libdivide::divider<uint64_t> fast_d(d);
    for (auto _ : stat) {
	    for (auto n : v) {
            benchmark::DoNotOptimize(n/=fast_d);
	    }
    }
}
BENCHMARK(bench_libdiv4);

// 场景3，除数已知但不是2的幂，特地选了一个素数23
void bench_div_const(benchmark::State &stat)
{
    std::random_device rd;
    std::mt19937 gen(rd());
    std::uniform_int_distribution<int64_t> dis(1, 114515);
    std::vector<int64_t> v;
    for (int i = 0; i < 10; ++i) {
	    v.push_back(dis(gen));
    }
    int64_t d = 23;
    for (auto _ : stat) {
	    for (auto n : v) {
            benchmark::DoNotOptimize(n/=d);
	    }
    }
}
BENCHMARK(bench_div_const);

void bench_libdiv_const(benchmark::State &stat)
{
    std::random_device rd;
    std::mt19937 gen(rd());
    std::uniform_int_distribution<int64_t> dis(1, 114515);
    std::vector<int64_t> v;
    for (int i = 0; i < 10; ++i) {
	    v.push_back(dis(gen));
    }
    libdivide::divider<int64_t> fast_d(23);
    for (auto _ : stat) {
	    for (auto n : v) {
            benchmark::DoNotOptimize(n/=fast_d);
	    }
    }
}
BENCHMARK(bench_libdiv_const);

BENCHMARK_MAIN();

测试内容是连续除十个随机生成的被除数，现代cpu性能还是很强悍的，如果只测除一次的情况，那么会得到一堆0.X纳秒的结果，那样对比不够明显，也容易引入统计误差和噪音。

测试运行也分两部分，一是使用-O2优化级别进行测试，在这个级别下编译器会采用比较保守的优化策略，并且只应用少量的SIMD指令；另一个是用-O3 -march=native进行优化，在这个级别下编译器会最大限度优化程序性能并且尽可能利用当前cpu上所有可用的指令（包括SIMD）进行优化。

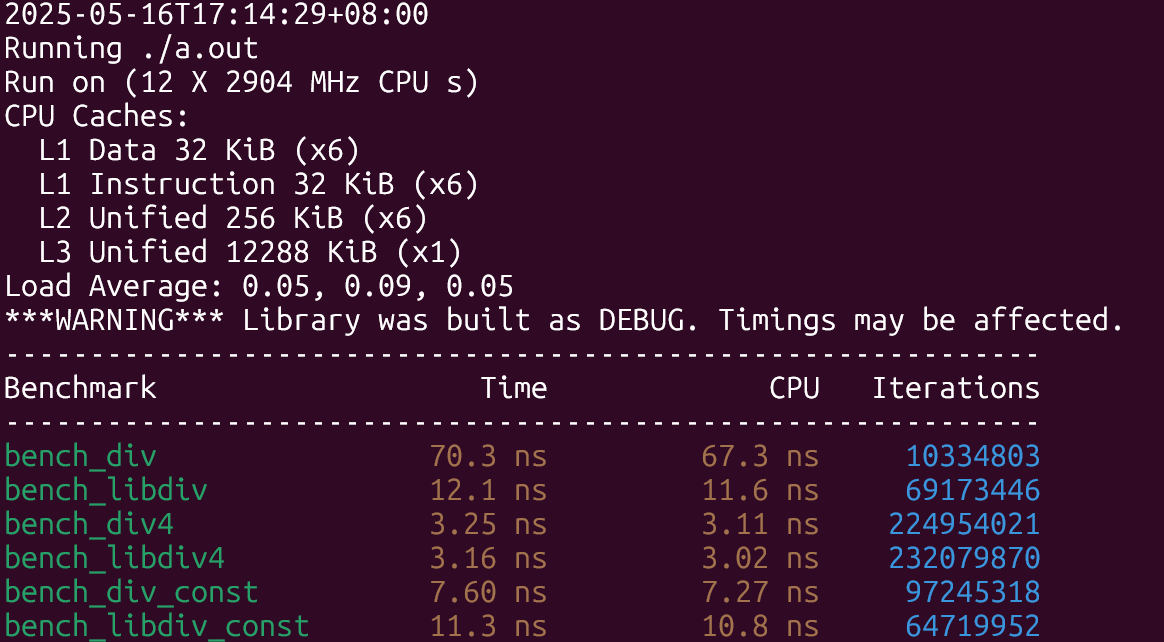
先来看看老机器上(10代i5台式机)的结果：

下面是开启native之后的结果：

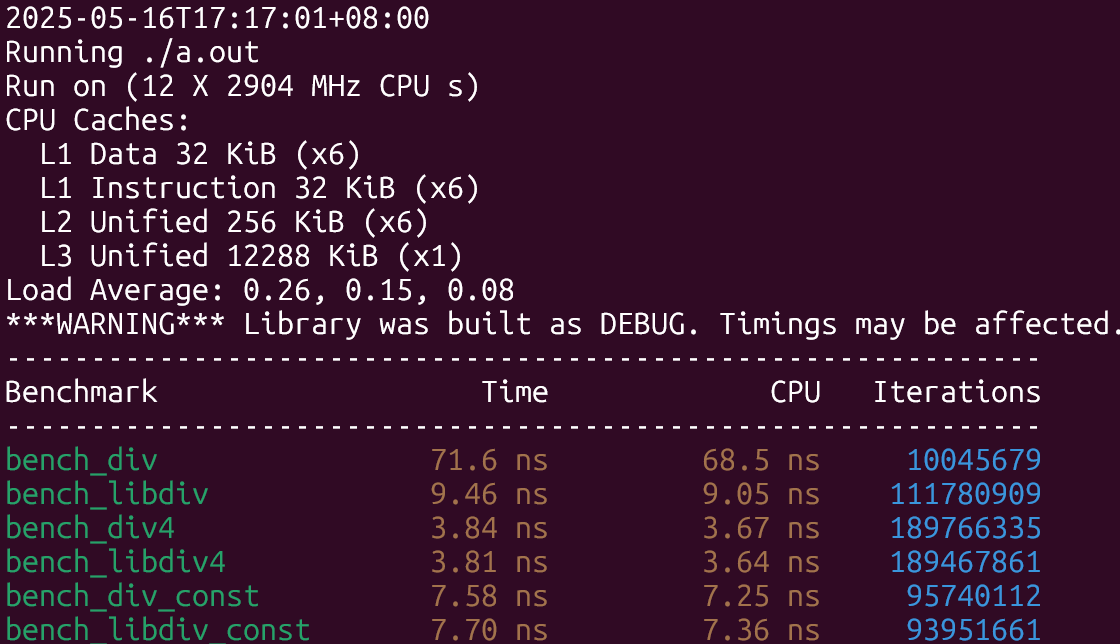
结果符合预期，在除数未知的情形下libdivide性能提升了8倍左右，除数已知且是2的幂的时候两者差不多，只有第三种情形下libdivide稍慢与直接除，原因大概是因为编译器也做了和libdivide类似的优化，但libdivide还需要额外探测除数的性质以及需要多几次函数调用，因此性能上稍慢了一些。

最大化利用SIMD结果类似，情形3下的差距缩小了很多。

然后我们看看在更新的机器上的表现（14代i7）：

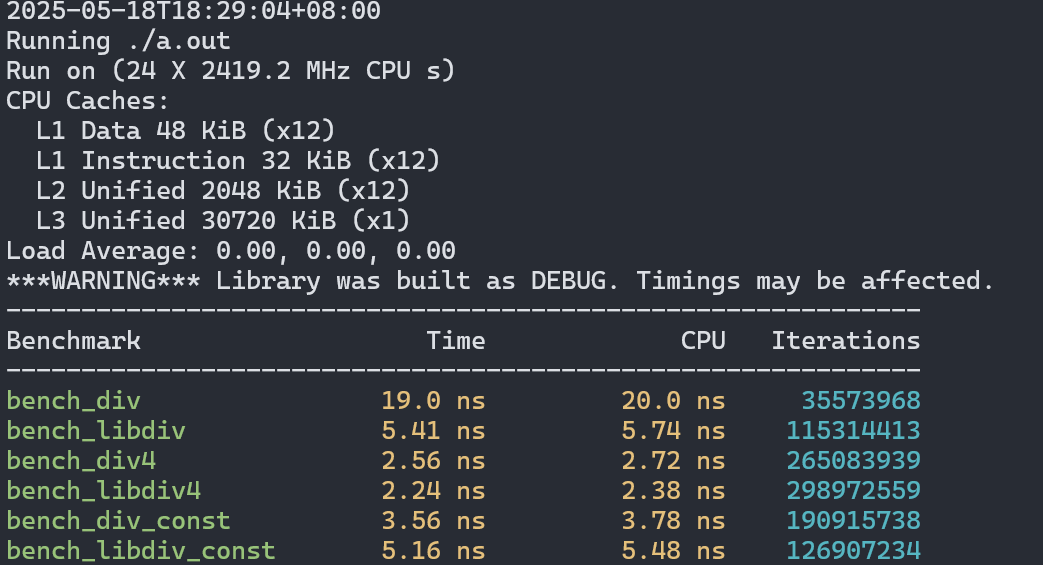
不启用最高级别优化时结果与老机器类似，但性能差距缩小了。

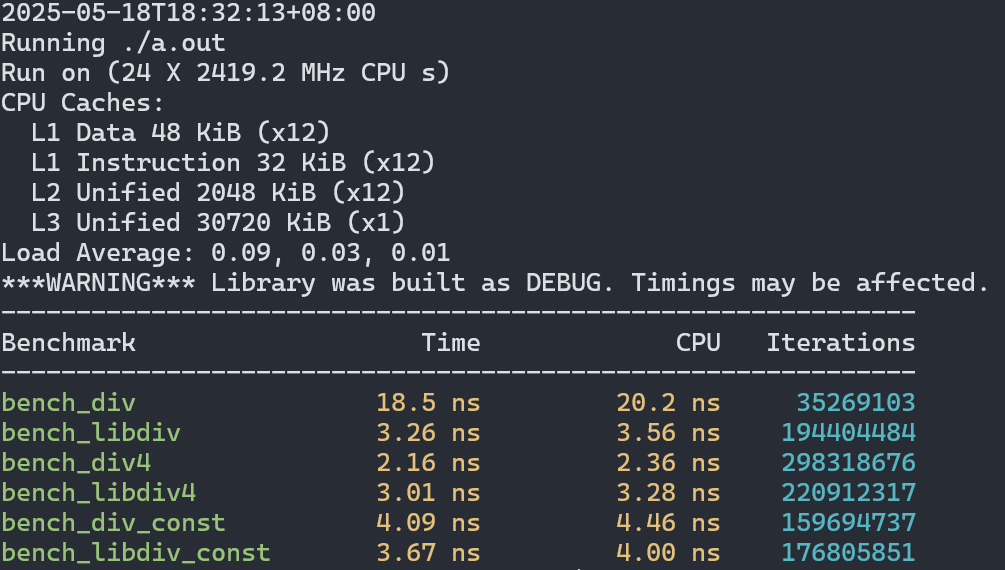
最大程度利用SIMD后现在情形3变快，但场景2又稍显落后了。在场景1中的提升也只有5倍左右。

总体来说在libdivide宣称的场景下，性能提升确实很可观，但还没到1个数量级这么夸张，不过我的测试环境都没有avx512支持，对于支持这个指令集的cpu来说也许性能还能再提升一些最终达到文档里说的10倍。在其他场景下libdivide的优势并不明显，所以追求极致性能的时候不是很建议在非场景1的情况下使用这个库。

总结

如果整数除法成为了性能瓶颈的话，可以尝试使用libdivide。这里总结下优缺点。

优点：

使用方便，只需要导入头文件
在除数未知的情况下能获得显著的性能提升
能利用SIMD，充分释放现代cpu性能

缺点：

只适用于除数未知的情况下
且除数要固定，因为频繁创建销毁libdivide::divider对象要付出额外的代价，会导致优化效果打折甚至负优化
libdivide::divider对象比整数要多占用一个字节，尽管这个对象是栈分配的，但对空间消耗比较敏感的程序可能需要谨慎使用，尤其是账面是虽然只多一字节，但遇到需要内存对齐的时候可能占用就要翻倍了。

总得来说libdivide还是很值得一试的库，但任何优化都要有性能测试做依据。