C++数据结构——红黑树

文章目录

- 一、背景
- 二、关键操作
- - [1. 旋转](#1. 旋转)
  - [2. 变色](#2. 变色)
  - [3. 查找](#3. 查找)
  - [4. 插入](#4. 插入)
  - [5. 删除](#5. 删除)
- 三、面试考点

一、背景

红黑树 （Red-Black Tree）是一种自平衡的二叉搜索树 （BST），通过颜色标记和旋转操作保证树的高度平衡，从而确保插入、删除、查找等操作的时间复杂度为 O ( l o g n ) O(log\ n) O(log n)。

其具有以下性质：

每个节点不是红色就是黑色；
根节点是黑色
叶子节点（NIL节点，空节点，一般默认不画出来）是黑色；
红色节点的子节点必须是黑色（即不允许连续红色节点）。
从任意节点到其所有叶子节点的路径中，黑色节点的数量相同（称为黑高相同）。

如下图所示（图取自参考1）：

红黑树的平衡是一种近似平衡，通过以上性质可以保证：树中没有一条路径会比其他路径长两倍。

原因：最短路径为全黑节点，最长路径为全黑结点每个后面插入一个红节点。

新插入的节点默认是红色（除非插入后成为根节点）。

原因：当前红黑树从根节点到叶节点的黑色节点数量已经一样了，如果插入新的黑色节点会破坏规则。但是如果加入的是红色节点，只有在父节点也是红色时才会破坏规则，更优。

红黑树的优势

其他的平衡树大多是完全平衡的，而红黑树是相对平衡的。

在插入/删除大量数据时，为了保持平衡，其他平衡树需要大量的旋转操作，而红黑树只需要少量的旋转操作。

在查找大量数据时，其他平衡树高度为 l o g n log\ n log n，而红黑树接近 2 l o g n 2log\ n 2log n，查找复杂度在一个数量级，差距不大。

红黑树的应用

epoll的实现
进程调度，内核CFS（Completely Fair Scheduler，完全公平调度器）队列
C++ STL的map和set
内存管理，如空闲链表freelist
Nginx的Timer时间管理

二、关键操作

1. 旋转

与Treap的旋转一样

（以下参考图来源于参考4）

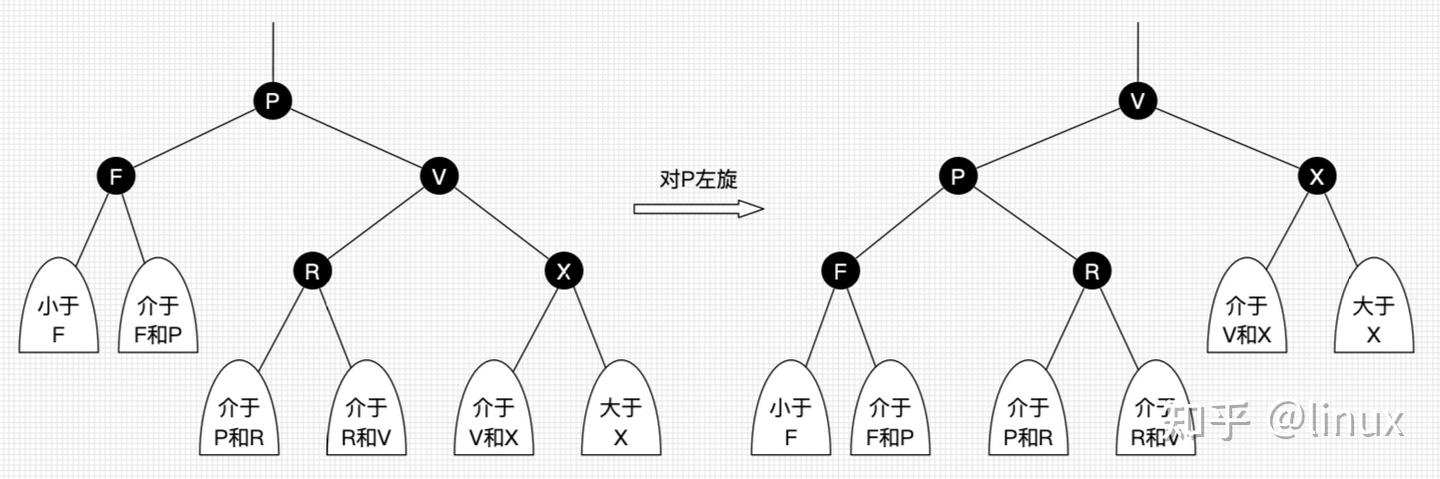
左旋

简化概括：将旋转节点变为右儿子的左儿子

具体操作：

将初始右儿子的左儿子接到旋转节点的右儿子
将旋转节点接到初始右儿子的左儿子上
初始右儿子到旋转节点的原位置

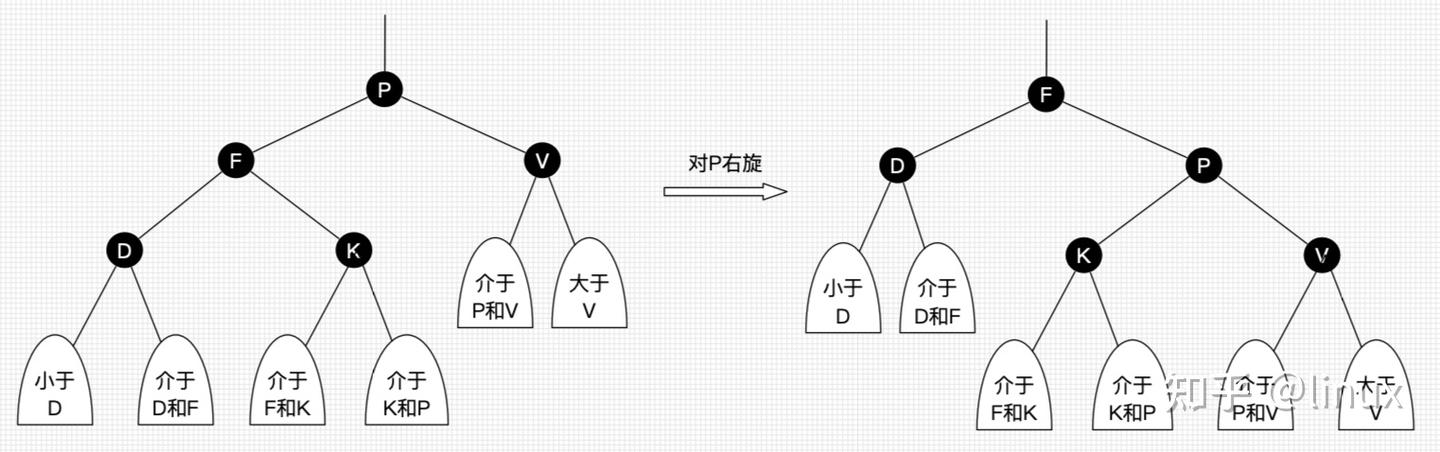
右旋

简化概括：将旋转节点变为其左儿子的右儿子

具体操作：

将初始左儿子的右儿子接到旋转节点的左儿子
将旋转节点接到初始左儿子的右儿子上
初始左儿子到旋转节点的原位置

2. 变色

变色操作是将节点的颜色改变，即红变黑、黑变红。

3. 查找

查找与一般BST相同

4. 插入

插入操作分为两大部分：查找待插入位置和自平衡

查找待插入位置与一般查找步骤类似。

自平衡过程，分情况讨论：

插入节点的父节点为黑色，新插入节点不会影响红黑树结构，不需要调整
插入节点的父节点为红色，则需要调整树结构：
- Case 1：叔节点（父节点的兄弟）为红色
  
  对非根爷爷节点、父节点、叔节点执行变色操作（将爷爷节点变为变为红色，父节点和叔节点变为黑色）；如果爷爷节点为根节点，则不变色。
  
  向上递归调整爷爷节点。
- Case 2：叔节点不存在
  - Case 2.1：插入节点和父节点同向，单旋+变色
    - RR：对爷爷节点左旋
    - LL：对爷爷节点右旋
    对父节点和爷爷节点变色
  - Case 2.2：插入节点和父节点异向，双旋+变色
    - RL（父右子左）：对父节点右旋，转为Case 2.1-RR
    - LR（父左子右）：对父节点左旋，转为Case 2.2-LL
    经过双旋后，父节点和爷爷节点变为了子节点，所以需要对插入节点和爷爷节点变色
- Case 3：叔节点存在且为黑色，该情况只会出现在Case 1的递归调整中，不会出现在新插入节点的情况下，该情况与Case 2操作相同

5. 删除

删除整体可分为两大步骤：删除该节点和自平衡。（参考4、5）

这里我们根据待删除节点子节点的数量分为三大情况：

Case 1：删除节点为叶子节点
- Case 1.1：删除节点为红色，不会影响红黑树的性质，可以直接删除
- Case 1.2：删除节点为黑色
  - Case 1.2.1：兄弟节点为黑色，且没有子节点
    
    如果父节点为红色，则变色为黑；兄弟节点变色为红
  - Case 1.2.2：兄弟节点为黑色，只有一个子节点
  - Case 1.2.3：兄弟节点为黑色，有两个子节点，且为红色
  - Case 1.2.4：兄弟节点为红色
Case 2：删除节点只有一个子节点

用子节点的值覆盖待删除节点的值，然后递归删除子节点
Case 3：删除节点有两个子节点

找待删除节点的前驱（左子树的最大值节点）或者后继（右子树的最小值节点），将前驱或者后继的值复制到该结点中，然后递归删除前驱或者后继；

三、面试考点

红黑树的性质是什么？如何保证平衡？
- 性质见一
- 平衡保证 ：
  - 通过颜色标记限制路径长度差异（最长路径不超过最短路径的2倍）。
  - 插入和删除时通过旋转和颜色调整修复性质冲突。
插入/删除后如何调整？分哪几种情况？

见二中的4和5
红黑树的时间复杂度是多少？为什么？
- 时间复杂度 ：插入、删除、查找均为 O(log n)。
- 原因：
  - 红黑树通过平衡性保证树的高度为 O(log n)（最长路径 ≤ 2倍最短路径）。
  - 每次操作最多需要从叶子到根的一次调整（最多旋转2次）。

红黑树和AVL树的区别？各自的优缺点？

特性	红黑树	AVL树
平衡性	宽松平衡（最长路径 ≤ 2倍最短路径）	严格平衡（左右子树高度差 ≤ 1）
旋转次数	插入/删除时旋转次数较少	插入/删除时旋转次数较多
适用场景	频繁插入删除（如Map、Set）	频繁查找（如数据库索引）
优点	插入删除效率高，适合动态数据	查询速度快，适合静态数据
缺点	查询稍慢（树更高）	插入删除成本高

如何实现红黑树的左旋/右旋操作？伪代码怎么写？

左旋C++代码：

cpp 复制代码

// 设_root为红黑树的根节点
void leftRotate(Node* node) {
    Node* tmpNode = node->right;  // 取node的右子节点为tmpNode
    
    // 将tmpNode的左子节点替换到node的右子节点，并处理父指针
    node->right = tmpNode->left;  
    if (node->right != nullptr) {
        node->right->parent = node;
    }
    
    // 处理node的父节点与tmpNode的关系
    tmpNode->parent = node->parent;
    if (node->parent == _root) {
        _root = tmpNode;
    } 
    else {
        if (node == node->parent->left) node->parent->left = tmpNode;
        else node->parent->right = tmpNode;
    }
    
    tmpNode->left = node;         // 将node节点替换到tmpNode的左子结点
    node->parent = tmpNode;       // 将node节点的父节点置为tmpNode
}

红黑树在哪些实际系统中被应用？

见一

参考：