传送门:https://www.luogu.com.cn/problem/P12542
题目大意:给定一个长为 n n n 的排列和一张 m m m 个点 e e e 条边的简单连通图。每次你可以在图上每个点设置一个 0 ∼ n − 1 0\sim n-1 0∼n−1、两两不同的权值发给交互库,交互库会从图中选择一条边,然后取出两个端点上的权值,作为排列的两个下标并进行交换。你可以随时停止游戏。
你要先求出:在两人的最优策略下,最终排列有多少个数归位(即 p [ i ] = i p[i]=i p[i]=i),你要让这个值最大化,交互库要让它最小化;并跟交互库玩这个游戏,在 3 n 3n 3n 次操作内至少达到这个最优解。
数据范围: m ≤ n ≤ 400 m\le n\le 400 m≤n≤400。
Warning:本题思维复杂性较高,阅读本题解之前请确保你处于大脑清醒的状态。
先看一些简单的 Case:
m = 2 m=2 m=2
相当于你可以每次直接交换排列的两个位置,那么就非常简单了:你只需要贪心地每次把一个数归位,至多 n − 1 n-1 n−1 次操作就可以让整个排列全部归位。
e > m e>m e>m
这是本题的第一个重要的观察:为什么 e > m e>m e>m 这个看起来很复杂的情况会放在第二个子任务而且只有 6 6 6 分?
答:此时你无能为力,初始排列直接就是最优解。
为什么?我们直接证明一个更强的结论:只要图中有 ≥ 3 \ge 3 ≥3 度的点,你就没有任何办法了。
考虑图中一个点 x x x 被设置为权值 t [ x ] t[x] t[x],如果选择的一条边与 x x x 相连,什么情况下会对答案产生正的贡献?只有两种情况:将 t [ x ] t[x] t[x] 这个数从别的位置交换回来;或者将 p [ t [ x ] ] p[t[x]] p[t[x]] 这个数交换到了它正确的位置上去。
由于图中所有的点权是两两不同的,因此上述两种情况在一个点 x x x 处都至多只有一条边满足。换句话说对于任意点而言,其相连的边中至多只有两条会让答案增加。
因此,如果图中存在 ≥ 3 \ge 3 ≥3 度的点,交互库就一定能选择其一条邻边,使得操作之后答案严格不增。因此你的一切努力都是徒劳的。
那么问题来了:一张简单连通图没有 ≥ 3 \ge 3 ≥3 度的点,有哪几种可能呢?只有两种可能:链或环。
此外,容易看出当未归位的点数不超过 m − 1 m-1 m−1 时,也无法更进一步了,因为将已经归位的点加入图中是没有意义的。这作为平凡的情形,后文中将不再讨论。
e = m − 1 e=m-1 e=m−1
链的情况,我们开始进行一些真正接近题目本质的分析。
对于任意排列 p p p 而言,可以建一张 n n n 个点的图,从每个点 i i i 向 p [ i ] p[i] p[i] 连边,那么得到的一定形如若干个环。其中大小为 1 1 1 的环表示已经归位的点,我们不去管它;考虑其它的环我们怎么处理。
假设我们交换了两个位置 ( i , j ) (i,j) (i,j),实际上就是在图中交换了这两个点的出边,对环结构的影响如下:
-
如果 i , j i,j i,j 原本不在同一个环上,这次交换会将两个环直接合并;
-
如果 i , j i,j i,j 原本在同一个环上,假设环大小为 p p p,两点在环上的距离为 q q q,则这次交换会将环拆分为两个环,大小分别为 q q q 和 p − q p-q p−q。
-
特别地,交换同一个环上相邻的两个位置会增加一个归位的点(因为多了一个大小为 1 1 1 的环)。
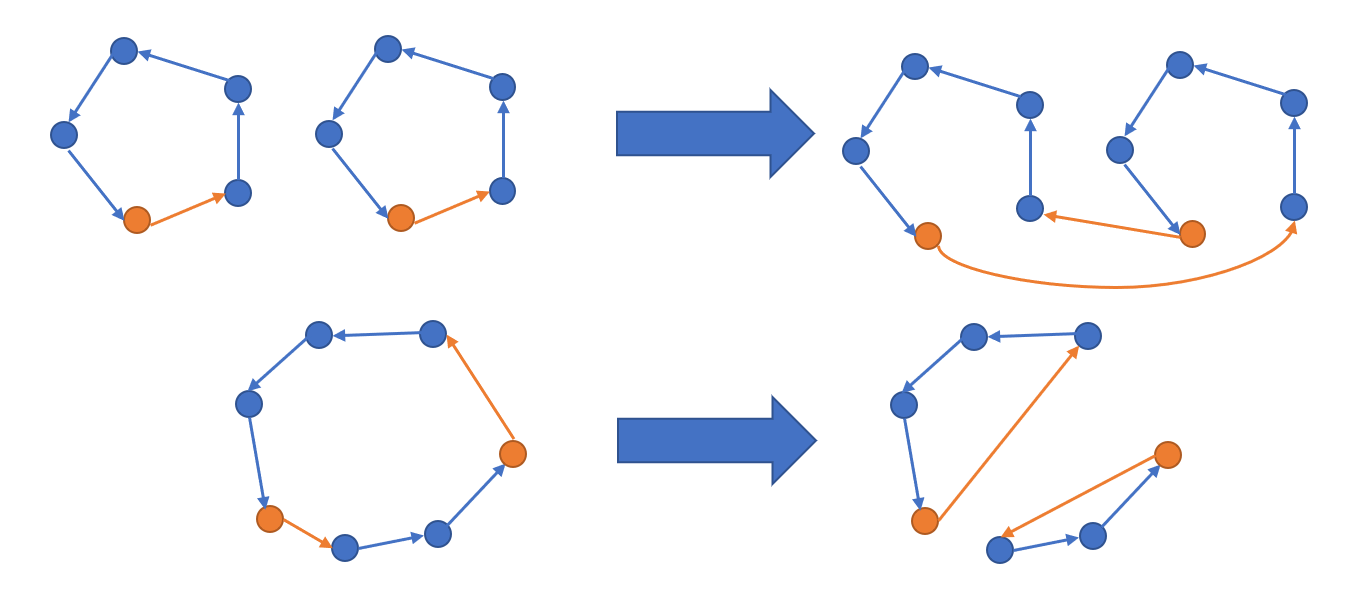
然后我们有如下几种操作:
-
"强制归位":对于一个大小 ≥ m \ge m ≥m 的环,只需要顺次选择环上 m m m 个相邻的点,交互库就必然要选择两个相邻点交换使得多一个点归位;
-
"强制合并":对于两个大小加起来 ≥ m \ge m ≥m 的环,可以在一个环上顺次选一些相邻的点,再在另一个环上顺次选一些相邻的点,这样交互库就要么选择一个环上的相邻两个点(这会让一个点归位)要么选择两个环上的点(这会合并这两个环)。这一操作也可以推广到多个环上,只要这些环大小之和 ≥ m \ge m ≥m,就逼迫交互库选择其中相邻两个环进行合并。

基于这两种操作我们可以轻松解决链的情况:只需要先将所有环全都合并起来,再每次强制归位一个点,就能操作到仅剩 m − 1 m-1 m−1 个点未归位。
e = m e=m e=m
接下来是环的情况,在展开更详细的分类讨论之前,首先要说明环相对于链的一些不同之处。
-
对于"强制合并"影响不大,只不过在多个环时让交互库多了一种将首尾两个环合并的选择;
-
然而对于"强制归位"的影响是关键的,因为这相当于在链的情形中增加了允许交互库选择链的首尾两个点,这会导致环断成两段而不是恰好拆出一个点。因此如果你还想达到强制归位的效果,就只能在大小恰好等于 m m m 的环上执行。
-
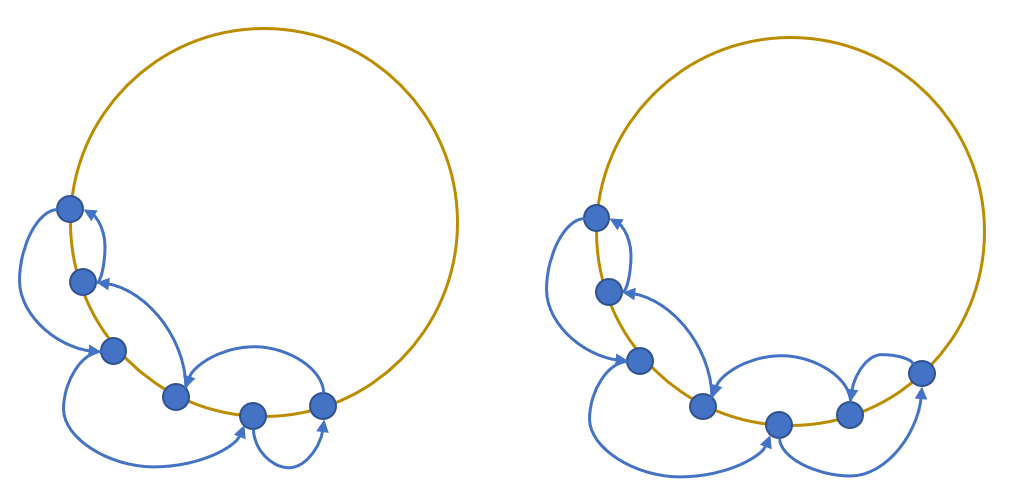
那么遇到更大的环该怎么办?为此我们必须开发出一种"强制拆分"操作:对于某个你想要的拆分距离 d d d,如果我们能在当前这个环上选取一系列点,使得(包括首尾在内,下同)相邻两个点的距离要么是 1 1 1 要么是 d d d,那么交互库为了不增加归位的点数就必须选择两个间距为 d d d 的点。如下图就是 d = 2 d=2 d=2 的情形,分为 m m m 是偶数/奇数两种情形,对应的选取序列分别为 0 , 2 , 4 , ... , m − 2 , m − 1 , m − 3 , ... , 1 0, 2, 4, \dots, m-2, m-1, m-3, \dots, 1 0,2,4,...,m−2,m−1,m−3,...,1 和 0 , 2 , 4 , ... , m − 1 , m − 2 , m − 4 , ... , 1 0, 2, 4, \dots, m-1, m-2, m-4, \dots,1 0,2,4,...,m−1,m−2,m−4,...,1。需要注意的是,这样的操作并不是我们随心所欲的,需要根据 m , d m,d m,d 和具体的环大小构造方案。
再讨论一些比较平凡的界:
-
对于剩余点数小于 m m m 的情形,显然没法继续操作了;
-
对于剩余点数恰为 m m m 的情形,可以将所有环合并成一个之后归位一次,得到剩余 m − 1 m-1 m−1 个点即为最优;
-
对于剩余点数恰为 m + 1 m+1 m+1 的情形,也没法更进一步了,因为想要更进一步就必须先搞出大小为 m m m 的环,但若果真如此那么剩下一个点已经自动归位了,于是就矛盾了。
那么问题来了:当剩余点数更多时,是否总能操作到只剩 m + 1 m+1 m+1 个点?我们需要进一步分类讨论。
e = m = 奇数 e=m=\texttt{奇数} e=m=奇数
先看 m m m 是奇数的情形。基于上面的"强制拆分"操作,我们知道一个大小为 m + 2 , m + 4 , ... m+2, m+4,\dots m+2,m+4,... 的环总能通过每次拆下两个点最终达到 m m m,从而可以进行一次归位。也就是说任何大小至少为 m m m 的奇环都能带来 1 1 1 的贡献。
那么偶环呢?很遗憾,对于偶环我们又无能为力了。具体而言,考虑当前排列里的奇环总数(包括大小为 1 1 1 的奇环),我们可以说明这个数量是无法增加的。
证明很简单:如果想使得奇环的数量增加,唯有将一个偶环拆分成两个奇环。然而如果我们将偶环进行间隔二染色,再选出 m m m 个点填入图中时,你会发现一定有相邻两个点是同色的。于是交互库只要选这两个点,就会将原先的偶环断成两个偶环。
基于上述分析,当前排列中奇环的数量就成了答案的上界。对于 m = 3 m=3 m=3 的情形,我们可以直接对所有的奇环每次进行 − 2 -2 −2 操作,直到变成 3 3 3 之后进行一次归位,就达到了这一最优解。
然而,当 m m m 是更大的奇数时,可能面临这样的问题:有一系列小于 m m m 的奇环,我们不能直接对其进行归位操作,只能先与其他环合并;然而合并两个奇环的操作是我们必须尽量避免的,因为这会使得答案上界 − 2 -2 −2。
所以我们可以优先取出一个最大的奇环,首先考虑将其与所有的偶环合并,直到大小不小于 m m m 为止;若合并上所有偶环之后大小仍然小于 m m m,我们就不得不从大到小选取若干个奇环进行合并,直到合并出不小于 m m m 的奇环为止。
注意到一旦合并出了第一个不小于 m m m 的奇环,后续就不再需要进行两个奇环之间的合并了,因为对其进行拆分和归位操作之后会得到大小为 m − 1 m-1 m−1 的偶环,在操作其他奇环时可以先将其与这个 m − 1 m-1 m−1 合并,以得到足够大的奇环执行后续操作;操作最终又会得到一个 m − 1 m-1 m−1 ,循环使用。
于是我们就完成了 m m m 为奇数的情形,注意到操作次数显然是够用的。
e = m = 4 e=m=4 e=m=4
来到了 m m m 是偶数的情形,为了更加清晰,我们先看一下 m = 4 m=4 m=4 的简单情形。
此时的理论上限是剩余 5 5 5 个点,这是可以达到的,接下来将给出一系列操作:
- 对于 4 4 4 元环可以归位一个点;
- 对于 ≥ 6 \ge 6 ≥6 的环,可以从中拆下来一个 4 4 4 元环,选取点的序列为 0 , 1 , 5 , 4 0, 1, 5, 4 0,1,5,4;
- 对于 5 5 5 元环,不能直接进行操作,必须先与任意一个环合并;
- 对于两个 2 2 2,可以合并成一个 4 4 4;
- 对于两个 3 3 3,可以合并成一个 6 6 6;
- 尽量不要合并 2 2 2 和 3 3 3,因为得到 5 5 5 是不优的。
请注意上面的第二个操作,它可以扩展为一般的偶数 m m m:对于任意 ≥ 3 m 2 \ge {3m \over 2} ≥23m 的环而言,都可以拆出一个 m m m,选取点的序列为 0 , 1 , 2 , ... , m 2 − 1 , 3 m 2 − 1 , 3 m 2 − 2 , ... , m 0, 1, 2, \dots, {m \over 2} - 1, {3m \over 2} - 1, {3m \over 2} - 2, \dots, m 0,1,2,...,2m−1,23m−1,23m−2,...,m。如下图分别为 m = 4 , 6 m=4, 6 m=4,6 的情形。
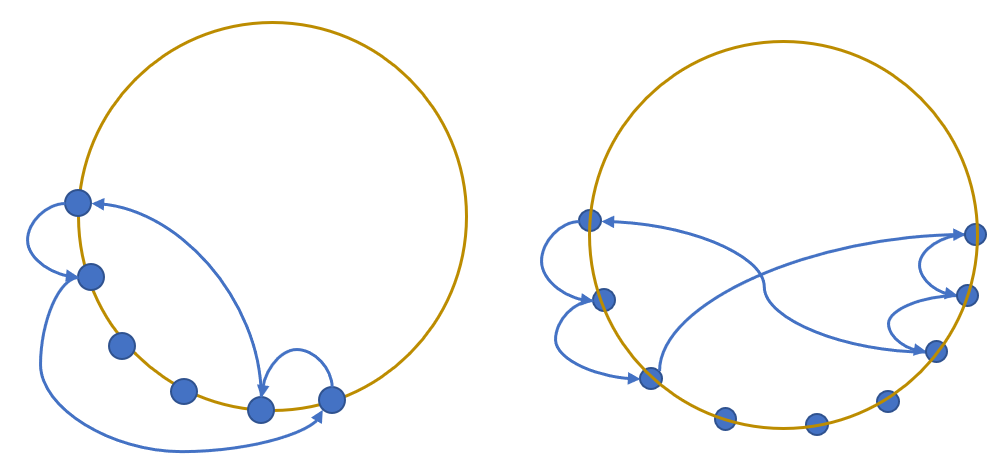
容易看出,只要按照上述操作序列依次执行,除合并 2 2 2 和 3 3 3 外,每 3 3 3 步之内一定能进行一次归位操作(可以自行验证)。因此只要我们不去合并 2 2 2 和 3 3 3(这在剩余点数多于 5 5 5 时总是可以的),就能一直操作下去直到只剩 5 5 5 个点为止,操作次数也是够用的。
e = m = 偶数 e=m=\texttt{偶数} e=m=偶数
终于到了最复杂的情形,我们首先要看一下 m m m 是一般的偶数相比 m = 4 m=4 m=4 时有哪些变化:最重要的变化是"强制拆分一个 m m m"只能适用于 ≥ 3 m 2 \ge {3m \over 2} ≥23m 的环(至少我并没有想到直接的适用于更小的环的拆分方案),因此我们需要重新设计将大小在 m + 2 ∼ 3 m 2 − 1 m+2 \sim {3m \over 2}-1 m+2∼23m−1 之间的环拆分成 m m m 的方案。
- 对于大小为 m + 2 , m + 4 , ... m+2,m+4,\dots m+2,m+4,... 的环,仍然可以每次拆分一个 2 2 2 出来,直到变成 m m m;
- 对于大小为 m + 3 , m + 5 , ... m+3,m+5,\dots m+3,m+5,... 的环,每次拆一个 2 2 2 只能最终达到 m + 3 m+3 m+3,再拆成 m + 1 m+1 m+1 是没有意义的。因此我们必须要设计从 m + 3 m+3 m+3 直接拆出一个 3 3 3 的策略。
具体方法是对 m m m 按照 m o d 6 \mod 6 mod6 分类讨论:
- m m o d 6 = 0 : 0 , 1 , 2 , 5 , 8 , ... , m − 1 , m − 2 , m − 3 , m − 6 , m − 5 , m − 8 , m − 9 , ... , 4 , 3 m \mod 6=0: 0, 1, 2, 5, 8, \dots, m-1, m-2, m-3, m-6, m-5, m-8, m-9, \dots, 4, 3 mmod6=0:0,1,2,5,8,...,m−1,m−2,m−3,m−6,m−5,m−8,m−9,...,4,3;
- m m o d 6 = 2 : 0 , 1 , 4 , 7 , ... , m − 1 , m − 2 , m − 3 , m − 6 , m − 5 , m − 8 , ... , 2 , 3 m \mod 6=2: 0, 1, 4, 7, \dots, m-1, m-2, m-3, m-6, m-5, m-8, \dots, 2, 3 mmod6=2:0,1,4,7,...,m−1,m−2,m−3,m−6,m−5,m−8,...,2,3;
- m m o d 6 = 4 : 0 , 3 , 6 , ... , m − 1 , m − 2 , m − 3 , m − 6 , m − 5 , m − 8 , ... , 2 , 1 m \mod 6=4: 0, 3, 6, \dots, m-1, m-2, m-3, m-6, m-5, m-8, \dots, 2, 1 mmod6=4:0,3,6,...,m−1,m−2,m−3,m−6,m−5,m−8,...,2,1。
分类讨论看着很繁琐,其实本质都是同一种方案:先 3 3 3 个 3 3 3 个往前跳,再按照 − 1 , − 3 , + 1 , − 3... -1, -3, +1, -3... −1,−3,+1,−3...的模式往回跳。下图中展示了 m = 6 , 8 , 10 m=6,8,10 m=6,8,10 的情形。另外,这种拆出 3 3 3 个点的构造对于更大的环而言也是适用的。
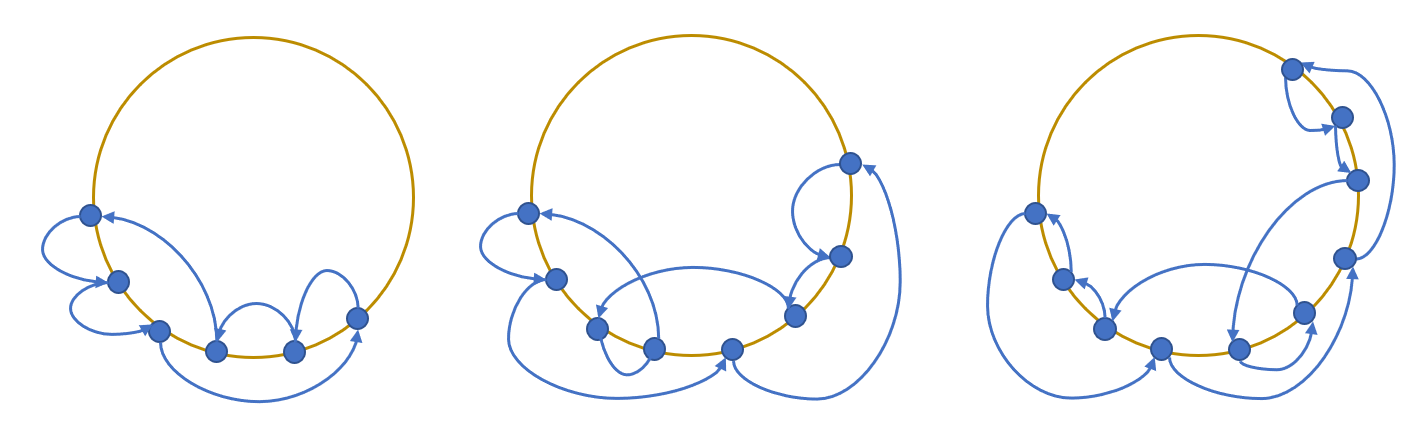
再加上对小环的合并操作,我们便可以达到剩余 m + 1 m+1 m+1 的最优解。但操作次数是否满足要求?
容易想到的操作序列如下:
- 如果存在一个 m m m,就进行一次归位;
- 如果有两个环大小之和为 m m m,合并之;
- 如果最大环 ≥ 3 m 2 \ge {3m \over 2} ≥23m,拆出一个 m m m;
- 如果最大环 ≥ m + 2 \ge m+2 ≥m+2 但 < 3 m 2 < {3m \over 2} <23m,拆出一个 2 2 2 或 3 3 3;
- 如果最大的环 = m + 1 =m+1 =m+1,就将其随便合并一个环(例如次大环);
- 如果最大的环 < m <m <m,就从大到小开始合并;例外是如果它与次大环加起来等于 m + 1 m+1 m+1,就去考虑合并更小的环,除非别无选择。
然而,这样实际上并不能达到 3 n 3n 3n 的操作次数限制!考虑当前剩余的一系列环为 m − 1 , 2 , 2 , ... , 2 m-1, 2, 2, \dots, 2 m−1,2,2,...,2,将执行如下一系列操作:
- 将 m − 1 m-1 m−1 和 2 2 2 合并为 m + 1 m+1 m+1;
- 将 m + 1 m+1 m+1 和 2 2 2 合并为 m + 3 m+3 m+3;
- 将 m + 3 m+3 m+3 拆分为 m m m 和 3 3 3;
- 对 m m m 执行一次归位变为 m − 1 m-1 m−1;
- 将 m − 1 m-1 m−1 和 3 3 3 合并为 m + 2 m+2 m+2;
- 将 m + 2 m+2 m+2 拆分为 m m m 和 2 2 2;
- 对 m m m 执行一次归位变为 m − 1 m-1 m−1。
总共使用 7 7 7 次操作进行了两次归位,除了 2 2 2 环少了一个外其他均不变,可知这样总的操作次数将达到 3.5 n 3.5n 3.5n 级别。
怎么办?容易发现这一操作序列即使处理 m = 4 m=4 m=4 也是不行的,需要回看当时是怎样避开这一问题的:现在相当于每次将 3 3 3 和 2 2 2 合并,然而这是我们不希望的,而当时是通过将两个 2 2 2 合并来避免了这一点。
这启发我们如果场上有 m − 2 m-2 m−2,就可以将其与 2 2 2 合并从而直接得到 m m m。然而 m − 1 m-1 m−1 是容易得到的( m m m 进行归位一次之后就天然得到 m − 1 m-1 m−1),但 m − 2 m-2 m−2 却并不容易得到。
再回看 m = 4 m=4 m=4 的情形,发现可以通过操作制造 2 2 2:将两个 3 3 3 合并得到 6 6 6,再将 6 6 6 拆分成 4 4 4 和 2 2 2。
因此,对于更大的 m m m,如果场上有两个 m − 1 m-1 m−1,就可以先合并得到 2 m − 2 2m-2 2m−2,再通过一次拆分得到 m m m 和 m − 2 m-2 m−2。这也正是这道题的最后一个关键处。而两个 m − 1 m-1 m−1 怎么得到?当然是从最初的一系列小环合并而来(或从更大的环上拆下来)。
总结上述的全过程,可以得到如下操作流程:
- 如果有 m m m,归位之;
- 如果有两个环大小之和为 m m m,合并之;
- 如果最大环 ≥ 3 m 2 \ge {3m \over 2} ≥23m,拆出一个 m m m;
- 如果最大环 ≥ m + 2 \ge m+2 ≥m+2 但 < 3 m 2 < {3m \over 2} <23m,拆出一个 2 2 2 或 3 3 3;
- 如果最大环 = m + 1 =m+1 =m+1,随便找一个环(如次大环)合并;
- 如果最大环 = m − 1 =m-1 =m−1 且次大环 = m − 1 =m-1 =m−1,合并二者;
- 如果最大环 = m − 1 =m-1 =m−1 且次大环 = m − 2 =m-2 =m−2,找出第三大环:如果为 2 2 2,则与 m − 2 m-2 m−2 合并(避免与 m − 1 m-1 m−1 合并得到 m + 1 m+1 m+1),否则与 m − 1 m-1 m−1 合并;
- 如果最大环 = m − 1 =m-1 =m−1 且次大环 < m − 2 <m-2 <m−2,就从次大环开始顺次合并(除非次大环与所有更小的环加起来已经不到 m m m 了,就将最大环与次大环合并);
- 如果最大环 < m − 1 <m-1 <m−1,就从最大环开始顺次合并。
分析总的操作次数:
我们要用 3 n 3n 3n 步归位不超过 n − m n-m n−m 个点,因此除了 "每 3 3 3 步归位一个点"以外,还有 3 m 3m 3m 步的冗余。
首先是最开始要合并出两个 m − 1 m-1 m−1,即使最初所有的环全是 2 2 2,这一步的额外开销不会超过 m m m;
其次进行主操作流程,直至剩余 2 m 2m 2m 个点以前一直能维持"(均摊下来)每 3 3 3 步归位一个点":只需额外分析当 m − 1 m-1 m−1 合并上一个不太大的环导致要进行一系列拆 2 , 3 2, 3 2,3 的操作,注意到这每一个 2 2 2 或 3 3 3 都能在后续步骤中省下来一步(例如 m − 2 m-2 m−2 和 2 2 2 仅需两步就能归位一个点; m − 1 , m − 2 , 3 m-1, m-2, 3 m−1,m−2,3 可以通过 5 5 5 步归位两个点),因此之前拆出来的操作都能被均摊掉;
最后是剩余 2 m 2m 2m 个点之后,必须回滚到之前的操作流程。采用回先前 3.5 3.5 3.5 步归位一个点的流程,加上可能有额外的 m 2 m \over 2 2m 步拆分 2 , 3 2, 3 2,3 的操作,总的额外开销不超过 m m m。
综上,在"每 3 3 3 步归位一个点"以外,总的额外开销不会超过 2 m 2m 2m,于是本题终于彻底做完了。
cpp
#include <bits/stdc++.h>
using namespace std;
int Bob(std::vector<int> t);
int m,e,n,nwas,cnt;
vector<int> u,v,p;
vector<int> vis,deg;
vector<vector<int>> cycles;
vector<int> cyc_id, cyc_size, cyc_pos; // 一个点所在的环编号、大小以及它在环上的位置
vector<int> cyc_list,cyc_odd,cyc_even; // 按从大到小的顺序排序后的所有环,后面两个是所有的奇环和偶环
vector<int> dfn,map_g; // dfn是图上节点编号的映射,map_g是dfn的逆
vector<vector<int>> edges; // 图上的边
vector<int> oper,oper_tmp; // 操作序列
void get_cycle(){ // 生成排列里所有的环
cycles.clear();
cyc_list.clear();
cyc_odd.clear();
cyc_even.clear();
nwas = 0;
memset(vis.data(),0,sizeof(int) * n);
for(int i = 0;i < n;++i) if(!vis[i]){
if(i == p[i]){ // 把已经归位的去掉
++nwas;
continue;
}
vector<int> q; q.clear(); q.push_back(i); vis[i] = 1;
for(int j = p[i];!vis[j];j = p[j]){
q.push_back(j); vis[j] = 1;
}
int cycle_id = cycles.size(); // 当前环的编号
cyc_list.push_back(cycle_id);
for(int j = 0;j < q.size();++j){
cyc_id[q[j]] = cycle_id; // 所在环编号
cyc_size[q[j]] = q.size(); // 所在环大小
cyc_pos[q[j]] = j; // 所在环上的位置
}
cycles.push_back(q);
}
// 按环长排序
sort(cyc_list.begin(),cyc_list.end(),[=](int x,int y){return cycles[x].size() > cycles[y].size();});
// 将环按奇偶分类
for(int i = 0;i < cyc_list.size();++i){
int x = cyc_list[i];
if(cycles[x].size() % 2) cyc_odd.push_back(x);
else cyc_even.push_back(x);
}
}
int nwdfn;
void dfs(int x){
map_g[x] = nwdfn;
dfn[nwdfn] = x;
++nwdfn;
for(int i = 0;i < edges[x].size();++i){
int y = edges[x][i];
if(map_g[y] != -1) continue;
dfs(y);
}
}
bool chk_deg(){
oper.resize(m); memset(oper.data(),0,sizeof(int) * m);
oper_tmp.resize(m); memset(oper_tmp.data(),0,sizeof(int) * m);
deg.resize(m); memset(deg.data(),0,sizeof(int) * m);
edges.resize(m);
for(int i = 0;i < m;++i) edges[i].clear();
for(int i = 0;i < e;++i){
++deg[u[i]];
++deg[v[i]];
edges[u[i]].push_back(v[i]);
edges[v[i]].push_back(u[i]);
}
for(int i = 0;i < m;++i) if(deg[i] >= 3) return 0;
// 求出图上点编号的映射关系
map_g.resize(m); memset(map_g.data(),-1,sizeof(int) * m);
dfn.resize(m); memset(dfn.data(),-1,sizeof(int) * m);
nwdfn = 0;
if(e == m - 1){ // 链的情况,要从1度点开始dfs
for(int i = 0;i < m;++i) if(deg[i] == 1){
dfs(i);break;
}
}
else dfs(0);
return 1;
}
int get_ans(){
get_cycle();
int ans = nwas;
if(!chk_deg()) return ans; // 有3度及以上的点就GG了
if(m == 2) return n; // 2个点
if(ans > n - m) return ans; // ans已经很大了
if(e == m - 1) return n - m + 1; // 链
if(ans == n - m) return n - m + 1; // 剩下刚好m个点没归位
if(m % 2 == 0) return n - m - 1; // 如果是偶数,则一定能剩下m+1个点
int nwsz = 0;
for(int i = 0;i < cycles.size();++i){
if(cycles[i].size() % 2 == 0) nwsz += cycles[i].size(); // 累加上所有偶环的大小
else ++ans; // 一个奇环意味着答案能+1
}
// 要从大到小检查这些奇环,直到能合并出来一个>=m的为止
bool fg = 0;
for(int i = 0;i < cyc_odd.size() && nwsz < m;++i){
int x = cyc_odd[i];
if(fg){ // 这个奇环已经要被合并了
nwsz += cycles[x].size();
fg = 0;
}
else if(cycles[x].size() + nwsz < m){ // 要付出2的代价合并两个奇环
ans -= 2;
nwsz += cycles[x].size();
fg = 1;
}
else break;
}
return ans;
}
inline void add_node(int &nw, int x){oper[dfn[nw++]] = x;} // 注意要套一层dfn
inline void add_node_cyc(int &nw, int x,int j){
add_node(nw,cycles[x][j]);
}
void get_m(int x){ // 从第x个环上切下长为m的一段来
// 0 1 2 ... m/2-1 3m/2-1 3m/2-2 ... m+1 m
int nw = 0;
for(int i = 0;i < m / 2;++i) add_node_cyc(nw,x,i);
for(int i = m / 2 - 1;i >= 0;--i) add_node_cyc(nw,x,i + m);
}
void get_3(int x){ // 从第x个环上切下长为3的一段来
int j;
int nw = 0;
for(j = 0;(m - j) % 3 != 1;++j){ // 前面%3多出来的部分
add_node_cyc(nw,x,j);
}
for(;j < m;j += 3){ // 间隔3个往前调
add_node_cyc(nw,x,j);
}
int fg = -1;
for(j = m - 2;j > 0;j -= 3 + fg){ // 从m-2开始,按照-1 -3 +1 -3 -1...的模式往回跳
add_node_cyc(nw,x,j);
add_node_cyc(nw,x,j + fg);
fg *= -1;
}
}
void get_2(int x){ // 从第x个环上切下长为2的一段来
int nw = 0;
// 1 3 5 ... m-1 m-2 m-4 ... 2 0
// 正着走,间隔2个放一个
for(int j = 1;j < m;j += 2){
add_node_cyc(nw,x,j);
}
// 倒着走,间隔2个放一个
for(int j = m - 2;j >= 0;j -= 2){
add_node_cyc(nw,x,j);
}
}
void gen_merge2(int x,int y){ // 合并两个环,大小之和至少是m
int nw = 0;
for(int j = 0;nw + 1 < m && j < cycles[x].size();++j){ // 第一个环最多放m-1个点
add_node_cyc(nw,x,j);
}
for(int j = 0;nw < m && j < cycles[y].size();++j){
add_node_cyc(nw,y,j);
}
}
void run(){ // 生成下一个操作序列,存在oper里
if(m == 2){ // 把第一个i!=p[i]的强制归位
for(int i = 0;i < n;++i) if(p[i] != i){
oper[0] = i;
oper[1] = p[i];
return;
}
}
if(e == m - 1 || nwas == n - m){
// 如果是链,或者剩余未归位的总点数恰好等于m,可以直接这么干
int nw = 0;
// 从大到小遍历所有的环,把点顺次加进操作序列
for(int i = 0;nw < m && i < cyc_list.size();++i){
int x = cyc_list[i];
for(int j = 0;nw < m && j < cycles[x].size();++j){
add_node_cyc(nw,x,j);
}
}
return;
}
int xx = -1;
for(int i = 0;i < cycles.size();++i) if(cycles[i].size() == m){
xx = i;break; // 找到了一个大小为m的环
}
if(xx != -1){ // 如果存在一个环刚好大小为m,就可以拆出来一个点
int nw = 0;
for(int j = 0;j < cycles[xx].size();++j){
add_node_cyc(nw,xx,j);
}
return;
}
if(m % 2 == 1){ // 奇环
// 由于还能继续操作,一定还有奇环
int x = cyc_odd[0];
int nw = 0;
if(cycles[x].size() > m){ // 第一个奇环足够大
// 0 2 4 ... m-1 m-2 m-4 ... 3 1
// 正着走,间隔2个放一个
for(int j = 0;j < m;j += 2){
add_node_cyc(nw,x,j);
}
// 倒着走,间隔2个放一个
for(int j = m - 2;j > 0;j -= 2){
add_node_cyc(nw,x,j);
}
return;
}
if(cycles[x].size() == m){ // 第一个奇环刚好是m,就强制拆出来一个点
for(int j = 0;j < cycles[x].size();++j){
add_node_cyc(nw,x,j);
}
return;
}
// 第一个环不够大
// 先把第一个环全都加进去
for(int j = 0;nw < m && j < cycles[x].size();++j){
add_node_cyc(nw,x,j);
}
// 然后把偶环加进去
for(int i = 0;nw < m && i < cyc_even.size();++i){
int x = cyc_even[i];
for(int j = 0;nw < m && j < cycles[x].size();++j){
add_node_cyc(nw,x,j);
}
}
// 最后再加入其余的奇环
for(int i = 1;nw < m && i < cyc_odd.size();++i){
int x = cyc_odd[i];
for(int j = 0;nw < m && j < cycles[x].size();++j){
add_node_cyc(nw,x,j);
}
}
}
else{ // 偶环
int x = cyc_list[0];
int nw = 0;
vector<int> sz;sz.resize(m);memset(sz.data(),-1,sizeof(int) * m);
for(int i = 0;i < cycles.size();++i) if(cycles[i].size() < m){
int nwsz = cycles[i].size();
if(sz[m - nwsz] != -1){ // 这两个环的大小之和刚好是m,合并之
int y = sz[m - nwsz];
gen_merge2(i,y);
return;
}
sz[nwsz] = i;
}
if(cycles[x].size() == m - 1){ // 第一个环是m-1,特殊情况
int y = cyc_list[1];
if(cycles[y].size() == m - 1){ // 第二个环也是m-1,那么把他俩合并
gen_merge2(x,y);
return;
}
int tot_nxt = 0;
for(int j = 1;j < cyc_list.size();++j)
tot_nxt += cycles[cyc_list[j]].size();
if(tot_nxt >= m){
int z = cyc_list[2];
if(cycles[y].size() + cycles[z].size() == m + 1){ // 这种情况让z和x合并
gen_merge2(x,y);
}
else{
// 把剩下的都合并到y上
for(int j = 1;nw < m && j < cyc_list.size();++j){
int w = cyc_list[j];
for(int k = 0;k < cycles[w].size() && nw < m;++k){
add_node_cyc(nw,w,k);
}
}
}
return;
}
// tot_nxt<m的情况不归这里考虑,回归到普通情形
}
if(cycles[x].size() < m){ // 第一个环不够大
// 从大到小遍历所有的环,把点顺次加进操作序列
for(int i = 0;nw < m && i < cyc_list.size();++i){
int x = cyc_list[i];
for(int j = 0;nw < m && j < cycles[x].size();++j){
add_node_cyc(nw,x,j);
}
}
return;
}
if(cycles[x].size() == m + 1){ // 第一个环刚好是m+1,消除不了,要融合进去下一个环
int y = cyc_list[1];
gen_merge2(x,y);
return;
}
if(cycles[x].size() >= 3 * m / 2){ // 第一个环特别大,允许拆出一个m
get_m(x);
return;
}
if(cycles[x].size() != m + 2 && cycles[x].size() != m + 4){ // 精细构造拆出一个3
// update:每次拆下来两个点会有问题,因为每次干掉一个点之后剩下的是m-1,就意味着还需要合并两个2才行
// 所以这里尽可能用了每次拆下来3个点的操作
get_3(x);
return;
}
// 第一个环足够大而且不是m+3,可以每次拆下来两个点
get_2(x);
}
}
int Alice(int _m, int _e, std::vector<int> _u, std::vector<int> _v, int _n, std::vector<int> _p){
m = _m, e = _e, n = _n;
u = _u, v = _v, p = _p;
vis.resize(n); memset(vis.data(),0,sizeof(int) * n);
cyc_id.resize(n); memset(cyc_id.data(),0,sizeof(int) * n);
cyc_size.resize(n); memset(cyc_size.data(),0,sizeof(int) * n);
cyc_pos.resize(n); memset(cyc_pos.data(),0,sizeof(int) * n);
int final_ans = get_ans();
cnt = 0;
while(nwas < final_ans){
++cnt;
run();
int res = Bob(oper);
swap(p[oper[u[res]]], p[oper[v[res]]]);
get_cycle(); // 重新生成环
}
return final_ans;
}