量子计算模拟：从理论到实践

量子计算作为现代物理学与计算机科学的前沿交叉领域，正逐渐从纯理论研究走向实际应用。本文将介绍一个基于Python的量子计算模拟框架，重点探讨量子比特、量子门操作以及量子态的演化等核心概念，并通过可视化手段直观展示量子态的特性。

量子计算的基本原理

量子计算利用量子力学的基本原理，如叠加态和纠缠态，来处理和存储信息。与经典计算中的比特只能处于0或1两种状态不同，量子比特可以同时处于0和1的叠加态，这种特性使得量子计算在特定问题上具有潜在的指数级加速能力。

量子计算的基本单位是量子比特（qubit）。一个量子比特的状态可以表示为：

\|\\psi\\rangle = \\alpha\|0\\rangle + \\beta\|1\\rangle

其中，\\alpha和\\beta是复数，且满足\|\\alpha\|\^2 + \|\\beta\|\^2 = 1。这表示当我们测量这个量子比特时，有\|\\alpha\|\^2的概率得到结果0，有\|\\beta\|\^2的概率得到结果1。

量子门操作

量子计算中的操作是通过量子门实现的。量子门是作用在量子比特上的酉变换，保持量子态的归一化。以下是几种基本的量子门：

1. Hadamard门（H门）：将基态转换为叠加态

H = \\frac{1}{\\sqrt{2}}\\begin{pmatrix} 1 \& 1 \\\\ 1 \& -1 \\end{pmatrix}

2. Pauli-X门（X门）：量子版的NOT门

X = \\begin{pmatrix} 0 \& 1 \\\\ 1 \& 0 \\end{pmatrix}

3. 相位门（Phase门）：改变量子态的相位

P(\\phi) = \\begin{pmatrix} 1 \& 0 \\\\ 0 \& e\^{i\\phi} \\end{pmatrix}

4. CNOT门：两量子比特门，根据控制比特的状态翻转目标比特

CNOT = \\begin{pmatrix} 1 \& 0 \& 0 \& 0 \\\\ 0 \& 1 \& 0 \& 0 \\\\ 0 \& 0 \& 0 \& 1 \\\\ 0 \& 0 \& 1 \& 0 \\end{pmatrix}

量子电路模拟器的实现

我们使用Python和QuTiP（Quantum Toolbox in Python）库实现了一个量子电路模拟器。以下是核心代码的关键部分：

class QuantumCircuit:
    def __init__(self, num_qubits):
        """初始化量子电路"""
        self.num_qubits = num_qubits
        self.state = tensor([basis(2, 0) for _ in range(num_qubits)])
        self.history = [self.state]
        
    def apply_hadamard(self, qubit):
        """应用Hadamard门"""
        h_matrix = 1/np.sqrt(2) * np.array([[1, 1], [1, -1]])
        h_gate = Qobj(h_matrix)
        
        ops = [qeye(2) for _ in range(self.num_qubits)]
        ops[qubit] = h_gate
        gate = tensor(ops)
        self.state = gate * self.state
        self.history.append(self.state)
        
    def apply_cnot(self, control, target):
        """应用CNOT门"""
        # 创建CNOT矩阵
        cnot_matrix = np.array([
            [1, 0, 0, 0],
            [0, 1, 0, 0],
            [0, 0, 0, 1],
            [0, 0, 1, 0]
        ])
        
        if self.num_qubits == 2 and control == 0 and target == 1:
            gate = Qobj(cnot_matrix, dims=[[2, 2], [2, 2]])
            self.state = gate * self.state
            self.history.append(self.state)
        else:
            raise NotImplementedError("目前仅支持2量子比特系统的CNOT门")
    
    def measure(self):
        """测量量子态"""
        return [abs(amp)**2 for amp in self.state.full().flatten()]

这个实现允许我们创建量子电路，应用基本的量子门操作，并测量最终的量子态。

量子态的可视化

量子态的可视化是理解量子计算的重要工具。我们实现了几种可视化方法：

1. 量子态概率分布

下图展示了Bell态（最大纠缠态）的概率分布。Bell态是形如(\|00\\rangle + \|11\\rangle)/\\sqrt{2}的量子态，测量时只有00和11两种结果，且概率均为50%。

2. 密度矩阵表示

密度矩阵是描述量子态的另一种方式，特别适合表示混合态。下图展示了Bell态密度矩阵的实部和虚部。

3. 布洛赫球表示

布洛赫球是表示单量子比特状态的几何方法。下图展示了Bell态中第一个量子比特的布洛赫球表示。由于纠缠的存在，单个量子比特处于完全混合态，表现为布洛赫球的中心点。

4. 量子态演化

下图展示了创建Bell态过程中量子态的演化。从初始的|00⟩态开始，经过Hadamard门和CNOT门的作用，最终形成Bell态。

高级量子态与现象

1. W态

W态是三量子比特系统中的一种纠缠态，形式为(\|001\\rangle + \|010\\rangle + \|100\\rangle)/\\sqrt{3}。与GHZ态不同，W态在失去一个量子比特后仍然保持部分纠缠。

2. 单量子比特叠加态

单量子比特可以处于不同的叠加态，如|+⟩、|−⟩、|+i⟩和|−i⟩态。这些态在布洛赫球上分别对应不同的位置。

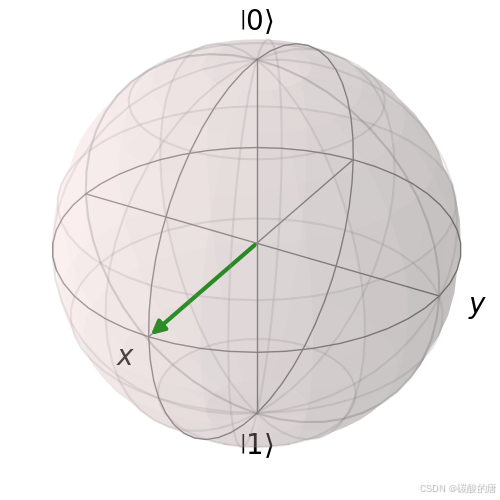
3. Wigner函数

Wigner函数是量子态在相空间的准概率分布，可以显示量子态的干涉和非经典特性。

量子算法实例：量子行走

量子行走是经典随机行走的量子版本，展示了量子干涉效应。在量子行走中，粒子可以同时向多个方向移动，导致与经典随机行走不同的概率分布。

量子行走算法的核心在于硬币算子（通常是Hadamard门）和条件位移算子的交替应用：

# 执行量子行走
for step in range(steps):
    # 应用硬币算子（Hadamard门）到硬币量子比特
    circuit.apply_hadamard(coin_qubit)
    
    # 应用条件位移算子
    # 如果硬币是|0⟩，则位置+1；如果硬币是|1⟩，则位置-1
    shift_gate = construct_shift_operator(num_position_qubits)
    circuit.state = shift_gate * circuit.state
    circuit.history.append(circuit.state)

量子纠缠与Bell态

量子纠缠是量子力学中最奇特的现象之一，两个或多个量子比特可以形成一个不可分离的整体，即使它们相距很远。Bell态是最简单的最大纠缠态，可以通过以下电路创建：

def create_bell_state():
    circuit = QuantumCircuit(2)
    circuit.apply_hadamard(0)  # 在第一个量子比特上应用H门
    circuit.apply_cnot(0, 1)   # 应用CNOT门，控制比特为0，目标比特为1
    return circuit

这个简单的电路创建了形如(\|00\\rangle + \|11\\rangle)/\\sqrt{2}的Bell态，这种态的特点是两个量子比特完全相关：测量一个量子比特会立即确定另一个量子比特的状态，无论它们相距多远。

量子相位估计算法

量子相位估计是许多量子算法的核心子程序，包括Shor算法。它的目标是估计酉算子的特征值的相位。

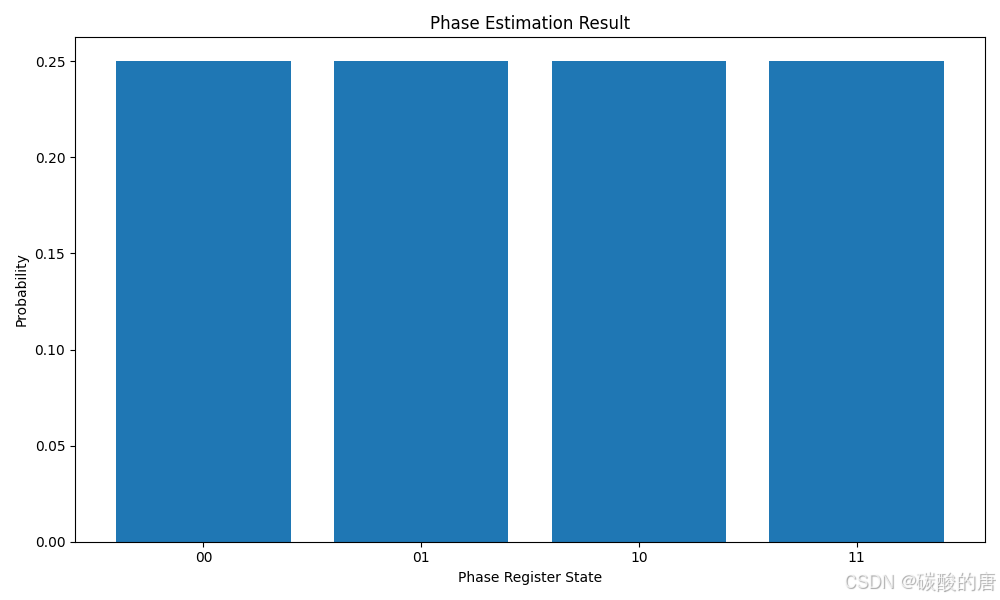
相位估计算法的基本步骤包括：

1. 准备相位寄存器和目标寄存器

2. 对相位寄存器应用Hadamard门

3. 应用受控酉操作

4. 应用逆量子傅里叶变换

5. 测量相位寄存器

结论与展望

量子计算模拟器为我们提供了一个探索量子计算原理的窗口，而无需实际的量子硬件。通过这些模拟，我们可以理解量子叠加、量子纠缠和量子干涉等现象，为未来量子算法的设计和实现奠定基础。

随着量子硬件的不断发展，我们期待量子计算能够在密码学、材料科学、药物设计等领域带来突破性进展。同时，量子模拟也将继续作为理解量子系统和开发量子算法的重要工具。

本文介绍的量子模拟框架虽然简单，但涵盖了量子计算的核心概念，可以作为深入研究量子计算的起点。未来的工作可以扩展到更多量子门、更复杂的量子算法以及噪声模型的引入，以更好地模拟真实量子计算机的行为。

参考文献

1. Nielsen, M. A., & Chuang, I. L. (2010). Quantum computation and quantum information. Cambridge university press.

2. Johansson, J. R., Nation, P. D., & Nori, F. (2012). QuTiP: An open-source Python framework for the dynamics of open quantum systems. Computer Physics Communications, 183(8), 1760-1772.

3. Mermin, N. D. (2007). Quantum computer science: an introduction. Cambridge University Press.

4. Preskill, J. (2018). Quantum Computing in the NISQ era and beyond. Quantum, 2, 79.