前言:
深夜的物流中心,十万件包裹在传送带上奔流不息。 扫描枪的嘀嗒声里,每个包裹的条形码都在呐喊:"把我送到正确的位置!"。
这像极了程序世界里的数据洪流------ 无序的数字渴望被归类,混沌的字符串等待被索引。 而二叉搜索树 ,正是程序员手中的智能分拣机: 它以**O(log n)**的优雅姿态,在数据洪流的惊涛中筑起秩序之岛。
但这座岛屿远非静态的乌托邦: 当包裹被退回(删除节点),当加急件突然插入(动态维护), 分拣机的齿轮如何咬合重组?指针的探照灯怎样校准路径?
本文将以C++为解剖刀,带你看清三个本质:
-
《轨迹》的烙印(节点插入的路径抉择)
-
《分裂》的艺术(数据删除的结构重组)
-
《逆鳞》的警示(平衡因子的崩溃预警)
这不是一篇温情的代码童话,而是一份快递员的操作手册------ 你的键盘就是扫描枪,你的递归函数就是分拣流水线。 当最后一个野指针被驯服时,你会听见编译器说: "数据已到达正确目的地"。
(抛弃游戏隐喻,转而用物流系统的精密机械感营造技术美学,同时保留周杰伦歌名的点睛之笔,形成独特的「工业诗性」风格)

1.准备工作
1.1.工作一
众所周知,链式结构的树是由一个个的节点构成的,之前小编在讲解二叉树的时候,我们首先需要定义好节点;二叉搜索树是一种特殊的二叉树,所以我们也是需要进行节点的定义,由于节点的难度不算大,小编就不详细说了,它的代码如下所示:
cpp
template<class K>
struct BSTNode
{
K _key; //节点里面存放的值
BSTNode<K>* _left; //左节点
BSTNode<K>* _right; //右节点
BSTNode(const K& key) //构造函数的书写
:_key(key)
, _left(nullptr)
, _right(nullptr)
{}
}; //先定义好二叉树的结点1.2.工作二
此时我们也需要把二叉搜索树的类进行框架的搭建,里面仅需存放根节点即可:
cpp
template<class K>
class BSTree
{
typedef BSTNode<K> Node;
private:
Node _root; //定义好根节点
};2.二叉搜索树的插入
cpp
bool Insert(const K& key)2.1.逻辑讲解
插入的实现逻辑其实很简单,我们只要记住:小的插入到左边,大的插入到右边这个特性,就可以很容易的去实现插入操作,不过此时我们有很多注意的点:
1.如果树本来就是空的,那么新插入的节点我们直接作为根节点即可。
2.树不是空的,那么就按照下面步骤走就可以了:如果插入的数据小于当前节点,那么我们往左边的树走;如果插入的数据大于当前节点,那么我们往右边的树走,直到找到空的位置,那么我们直接插入即可。
3.相等的数据我们就不考虑了,如果各位想要考虑,那么可以参考下面的逻辑:可以让相等的节点统一往左边进行插入,直到找到空位置(此时我们需要保持逻辑一致,不要一会插入左边,一会又到右边了)。
2.2.代码实现
此时我们一步一步走,需要通过if语句进行树的判断,如果此时树是空的(即根节点是空的),那么我们就直接开辟一个节点,让这个节点作为根节点即可:
cpp
if (_root == nullptr)
{
_root = new Node(key);
return true;
}如果树不是空的,那么我们就按照步骤一步一步的走,此时我们需要定义好一个父节点和一个要进行遍历的节点,后面各位读者朋友可能会理解,因为我们需要确定根节点是不会被污染的;父节点存在的意义是因为此时我们插入节点以后,如果没有和上一个节点建立关系,那么此时这个节点实际上是不会被插入到二叉树中的,这个点各位要注意,此时我们根据上面的逻辑,通过while循环以及if语句进行插入代码的实现。
cpp
Node* parent = nullptr; //此时的Node是我把上面的节点进行typedef过的,各位不要理解错了~
Node* cur = _root;
while (cur)
{
if (key < cur->_key) //判断此时的值是否小于当前节点,如果小于
{
parent = cur; //父节点记录当前的位置,方便之后建立关联
cur = cur->_left; //那么就往左边走
}
else if (key > cur->_key) //判断此时的值是否大于当前节点,如果大于
{
parent = cur; //父节点记录当前位置的值,方便之后联系的建立
cur = cur->_right; //那么就往右边走
}
else
{
return false; //相等的值暂且让他消失 //咱就不考虑相等的了,比较麻烦
}
}
//到这里就说明此时已经找到了,此时直接先设置好一个结点就好了
cur = new Node(key); //这个想必各位都不陌生,陌生的话可以看我之前的文章
if (key > parent->_key) //当然,插入节点的时候也需要判断此时是插入到父节点的左边还是右边
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
return true;2.3.完整代码
cpp
bool Insert(const K& key)
{
if (_root == nullptr)
{
_root = new Node(key);
return true;
}
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (key < cur->_key)
{
parent = cur;
cur = cur->_left;
}
else if (key > cur->_key)
{
parent = cur;
cur = cur->_right;
}
else
{
return false; //相等的值暂且让他消失
}
}
//到这里就说明此时已经找到了,此时直接先设置好一个结点就好了
cur = new Node(key);
if (key > parent->_key)
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
return true;
}3.二叉搜索树的查找
cpp
bool Find(const K& key);3.1.逻辑讲解
其实我个人认为二叉搜索树的查找逻辑是最为简单的,因为它其实就是类似上面的插入逻辑,不过二者最大的区别就是查找是不需要再插入新的节点了,其余的其实都一样,我们依然是先设置好一个节点代替根节点进行树的遍历,如果要找的值比当前节点小,就往左边走;如果比当前节点大,就往右边走;如果相等的话,那么就可以返回true了(此时就是判断这个节点是否在这树上)。这就是本功能的逻辑讲解,下面直接看代码部分。
3.2.代码书写
此时,我们需要设置好一个节点作为遍历二叉树的节点。
cpp
Node* cur = _root;之后我们就可以通过循环的方式进行值的查找,如果要查询的值比当时节点的值小,就让cur往左走;反之则往右边走;如果找到了,直接返回true即可;如果没有找到的话,直接返回false即可。
cpp
while (cur)
{
if (key > cur->_key)
{
cur = cur->_right;
}
else if (key < cur->_key)
{
cur = cur->_left;
}
else
{
//找到了
return true;
}
}
return false; //没找到3.3.完整代码
cpp
bool Find(const K& key)
{
Node* cur = _root;
//循环的查询
while (cur)
{
if (key > cur->_key)
{
cur = cur->_right;
}
else if (key < cur->_key)
{
cur = cur->_left;
}
else
{
//找到了
return true;
}
}
return false; //没找到
}4.二叉搜索树的删除
cpp
bool Erase(const K& key)4.1.逻辑分析
朋友们,本博客中最阴间的部分来了,二叉搜索树的删除可以说是整个二叉搜索树实现过程中最麻烦的部分,因为它并不能单纯的删除,它还要让二叉搜索树的性质不可以被破坏(以后我要讲的AVL树的删除也很麻烦,不过我选择不讲,因为我也没搞懂(#^.^#)),所以删除我们需要分以下几种情况。
1.要删除的节点是个叶子结点(左右孩子均为空)【难度系数:⭐】
这个是我最爱的删除情况了,因为它被删除以后仅需让它的父亲节点指向空以后,直接删除节点即可。这个情况是最容易的,因为不用顾及儿女。
2.要删除的节点左孩子为空,但是右孩子不为空【难度系数:⭐⭐】
这个算是比较难的,但是也是很容易解决的,就比如小王就是要被删除的节点,他有一个孩子叫做小禾;有一天小王因为工作要去外地出差,但是他的孩子需要被别人照顾,此时我们仅需让其父母即父节点来照顾小禾即可;此时我们仅需看要把小禾作为爷爷的左边还是右边即可。
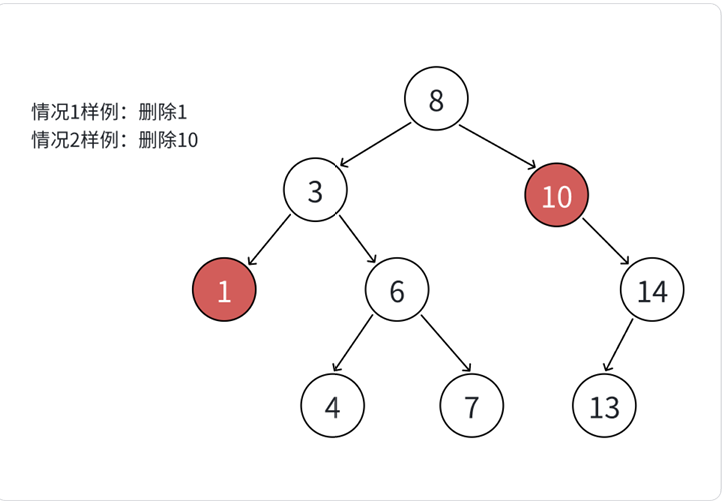
3.要删除的节点右孩子为空,但是左孩子不为空【难度系数:⭐⭐】
这个和2是一个情况,参考上面即可。最后就是把小王的父亲对应孩子指针指向小禾,直接删除N结点。

4.要删除的节点有俩孩子【难度系数:⭐⭐⭐⭐】
这个是我认为最为复杂的情况,因为此时我们如果还是根据上面的情况进行删除的话,那么就会遇到一个尴尬情况:删除节点的父母节点不可能一下子接受两个孩子。所以此时我们需要换一种方法:替换法。
此方法我认为可以称得上妙计,因为我们需要保持二叉树的结构,所以我们删除需要谨慎,对于这种直接删除困难的情况,我们可以使用替换法来进行问题的解决,以下图为例。

此时如果我们要删掉3这个节点,我们可以用右子树的最小节点来和它进行替换,因为无论是3还是右子树最小节点(上图为4)放到这个位置都很合适,而右子树最左节点正好适合上面的1,2,3这三类情况,不过后续小编代码实现的时候,会把1并入到2和3,此时我们仅需让4节点的父母节点指向它的左或右【视情况而定】即可,此时我们就是实现了对于3的删除。其实这个方法各位理解完以后就会觉得还挺容易的。
以上便是删除的大致逻辑,和之前实现的功能一比,删除功能是比较复杂的,它的代码实现也是充满着坑,不过都不要紧,我相信各位理解完上述的方法后,至少1,2,3出错的概率比较小,至于4可能会踩坑,但是有我在,我保证让各位都避免掉入坑。
4.2.代码实现
本功能实现的最大前提是我们需要确定此时我们想要删除的值是否在这棵树里面,我们可以复用上面的查找功能(直接把代码copy过来即可),直到找到了节点,我们就可以开始进行删除;如果没有找到,我们皆可以直接返回false了。
cpp
Node* parent = nullptr;
Node* cur = _root;
//查询找到节点
while (cur)
{
if (key > cur->_key)
{
parent = cur;
cur = cur->_right;
}
else if (key < cur->_key)
{
parent = cur;
cur = cur->_left;
}
else
{
//等会我们就要在这里实现删除功能
}
}
return false; //没找到找到节点以后,我们就可以进行删除操作了,此时我们需要分为三种情况判断:1.该节点只有右孩子;2.该节点只有左孩子;3.该节点俩孩子都有【没有孩子并入到1,2】。
1.只有右孩子
此时我们要判断该节点是否就是根节点,如果就是根节点的话,那么我们直接让右孩子作为根节点之后,再把当前节点删除即可。
cpp
//开始删除
if (cur->_left == nullptr)
{
if (cur == _root)
{
_root = cur->_right; //等会统一删除
}
else
{
//下面实现
}
}如果不是根节点的话,那么我们仅需判断当前节点是父亲节点的左还是右即可,然后让孩子继承到父亲节点左/右即可。
cpp
if (cur == parent->_left)
{
parent->_left = cur->_right;
}
else
{
parent->_right = cur->_right;
}之后我们进行统一删除即可。
cpp
delete cur;
return true;完整代码
cpp
if (cur->_left == nullptr)
{
if (cur == _root)
{
_root = cur->_right;
}
else
{
if (cur == parent->_left)
{
parent->_left = cur->_right;
}
else
{
parent->_right = cur->_right;
}
}
delete cur;
return true;
}2.只有左孩子
它的逻辑和上面是一样的,这里我就不细说了,直接上代码了(理解了上面的话实现这一部分很容易,如果不理解的话可以文章末加上我的微信询问我)。
cpp
else if (cur->_right == nullptr)
{
if (cur == _root)
{
_root = cur->_left;
}
else
{
if (cur == parent->_left)
{
parent->_left = cur->_left;
}
else
{
parent->_right = cur->_left;
}
}
delete cur;
return true;
}3.左右孩子都有
这部分实现还是比较麻烦的,此时我们首先先定义好两个节点,分别作为右子树最小的节点以及它的父节点。
cpp
Node* minRightParent = cur;
Node* minRight = cur->_right;之后我们通过然让minright循环找到其最左节点,一定记得让其父节点在节点循环之前等于该节点,不然等会出大错;之后我们就让要被替换节点的值把要删除节点的值覆盖掉,之后我们在把当前节点删除即可,此时我们仍需判断此时节点的值是符合上面两种情况即可。
cpp
//找到左边最小的节点,经过替换把他删掉
while (minRight->_left)
{
minRightParent = minRight;
minRight = minRight->_left;
}
cur->_key = minRight->_key; //直接值替换就好了
if (minRightParent->_left == minRight)
{
minRightParent->_left = minRight->_right;
}
else if(minRightParent->_right == minRight)
{
minRightParent->_right = minRight->_right;
}
delete minRight;
return true;完整代码
cpp
Node* minRightParent = cur;
Node* minRight = cur->_right;
//找到左边最小的节点,经过替换把他删掉
while (minRight->_left)
{
minRightParent = minRight;
minRight = minRight->_left;
}
cur->_key = minRight->_key; //直接值替换就好了
if (minRightParent->_left == minRight)
{
minRightParent->_left = minRight->_right;
}
else if(minRightParent->_right == minRight)
{
minRightParent->_right = minRight->_right;
}
delete minRight;
return true;5.关于二叉搜索树的更改
二叉搜索树就像周杰伦演唱会的座位分区🎤,每个区域都按「粉丝身高许可证」严格划分:左边必须全是《可爱女人》式娇小甜妹,右边必须是《双截棍》猛男团。
要是你手欠把某个座位区粉丝的身高偷偷改了(比如让中间VIP区突然冒出一个两米八的姚明分明),《粉色海洋》瞬间变《斗牛》现场------左边甜妹集体怒吼💢:「凭啥你突然比我的《简单爱》还高调?」右边猛男直接《龙拳》警告⚠️:「你篡改数据是想抢《三年二班》的篮球框吗?」
于是整个演唱会从《安静》的星空灯海✨,炸成《逆战》的混乱战场💥,查票效率从《超跑女神》🏎️暴跌到《蜗牛》🐌爬!所以想调整二叉搜索树?必须走《听妈妈的话》流程:先《退后》删除,再《晴天》插入,才能维持《最伟大的作品》秩序啊!🎧🕺
简单来说,如果我们随意更改二叉搜索树,就会让这个结构不再是二叉搜索树的结构,为了保持二叉搜索树的特性,所以我们不可以修改二叉搜索树,这点各位读者要记住。

6.完整代码
Binarysearchtree.hpp
cpp
#pragma once
#include<iostream>
#include<string>
using namespace std;
namespace wang
{
template<class K>
struct BSTNode
{
K _key;
BSTNode<K>* _left;
BSTNode<K>* _right;
BSTNode(const K& key)
:_key(key)
, _left(nullptr)
, _right(nullptr)
{}
}; //先定义好二叉树的结点
template<class K>
class BSTree
{
typedef BSTNode<K> Node; //这里为了方便表示
public:
bool Insert(const K& key)
{
if (_root == nullptr)
{
_root = new Node(key);
return true;
}
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (key < cur->_key)
{
parent = cur;
cur = cur->_left;
}
else if (key > cur->_key)
{
parent = cur;
cur = cur->_right;
}
else
{
return false; //相等的值暂且让他消失
}
}
//到这里就说明此时已经找到了,此时直接先设置好一个结点就好了
cur = new Node(key);
if (key > parent->_key)
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
return true;
}
//查询功能,找到想要的结点
bool Find(const K& key)
{
Node* cur = _root;
//循环的查询
while (_root)
{
if (key > _root->_key)
{
_root = _root->_right;
}
else if (key < _root->_key)
{
_root = _root->_left;
}
else
{
//找到了
return true;
}
}
return false; //没找到
}
//删除某一个结点
bool Erase(const K& key)
{
Node* parent = nullptr;
Node* cur = _root;
//查询找到节点
while (cur)
{
if (key > cur->_key)
{
parent = cur;
cur = cur->_right;
}
else if (key < cur->_key)
{
parent = cur;
cur = cur->_left;
}
else
{
//叶子节点或者只有=右孩子
//开始删除
if (cur->_left == nullptr)
{
if (cur == _root)
{
_root = cur->_right;
}
else
{
if (cur == parent->_left)
{
parent->_left = cur->_right;
}
else
{
parent->_right = cur->_right;
}
}
delete cur;
return true;
}
//只有做孩子
else if (cur->_right == nullptr)
{
if (cur == _root)
{
_root = cur->_left;
}
else
{
if (cur == parent->_left)
{
parent->_left = cur->_left;
}
else
{
parent->_right = cur->_left;
}
}
delete cur;
return true;
}
//俩孩子都有,直接替换
else
{
Node* minRightParent = cur;
Node* minRight = cur->_right;
//找到左边最小的节点,经过替换把他删掉
while (minRight->_left)
{
minRightParent = minRight;
minRight = minRight->_left;
}
cur->_key = minRight->_key; //直接值替换就好了
if (minRightParent->_left == minRight)
{
minRightParent->_left = minRight->_right;
}
else if(minRightParent->_right == minRight)
{
minRightParent->_right = minRight->_right;
}
delete minRight;
return true;
}
}
}
return false; //没找到
}
void InOrder()
{
_InOrder(_root);
cout << endl;
}
private:
void _InOrder(Node* root)
{
if (root == nullptr)
{
return;
}
_InOrder(root->_left);
cout << root->_key << " ";
_InOrder(root->_right);
}
Node* _root = nullptr;
};
}7.结语
本文到这里也就结束了,不知道改为读者觉得我写的怎么样,如果感觉小编写的不错的话,那么各位大佬们可以多多给小编点赞,小编到这里也就感谢各位大佬的点赞喽~二叉搜索树的实现其实各位只要理解了它的逻辑,代码实现还是很容易的,希望各位读者可以看完本文后多多练习,学习的时光总是短暂的,那么各位大佬们,我们下一篇文章见啦!
