一、链表的分类
迟来的分类,主要如果在学习单链表前去讲分类,可能就云里雾里的,所以放在讲完单链表后讲。
划分链表的标准如下:

有没有头结点、指针的方向、循环与否
头结点就是一个占位结点,也被叫做哨兵位,一般就是标识起点、防止链表为空,本身不储存任何有效元素(就类似于我们高速上看到的,前方多少米服务区,前方多少米进入什么地界,碰到头结点就知道遍历到链表的头结点了)。
指针方向一个是只能从前往后遍历,另外一个双向的就是既有指向前一个结点的指针,也有指向后一个结点的指针。
循环与否,就看逻辑上的尾结点的next指针,如果重新指向了头结点,那么就是循环链表,如果为NULL,那就不是循环链表。
如图所示:

我们学过的单链表其实如果把这几个属性带上的话就是单向不带头不循环链表。
今天我们学的双向链表可以叫做双向带头循环链表。
所以如果硬说的话,链表应该是八种,我们学习的话,只学一个最简单的单链表,再学一个最复杂的双向链表。
二、双向链表
1.双向链表的概念与结构
基本不用说什么了,带头结点,循环,指针双向:

2.双向链表的实现

3.双向链表的初始化
双向链表的初始化无非就是先创建一个头结点
所以写一个创建结点的函数也是有必要的(同单链表的buynode)
头结点的结构是什么样的呢?
头结点的值倒是无所谓,毕竟头结点的值无效。
而由于我们双向链表是循环的,所以指针肯定得循环起来,因此初始化成这个状态:

代码实现:

核心逻辑就是我们的Buynode方法,既然我们创建的新的结点有可能是头结点,有可能是其他节点。
如果是头结点,我们肯定是在Init方法中调用的,该结点应当自循环;
如果不是头结点,既然能创造出来,一定是做插入之类的操作,因为创建新结点后我们就会返回地址,到时候肯定还能顺着地址修改,所以buynode方法的指针指向其实是无所谓的,只要你data给我设计对了即可。
测试Init方法:

没啥毛病。
4.双向链表的插入操作
双向链表的尾插
不必多说,上来就是尾插,画图看看需要怎么写:

上来肯定是创建个新结点。
然后就得改指针了呗,看看哪些指针需要修改:

newnode想往里尾插,那它就是新的尾结点,原来的尾结点的next指针就得变为newnode,原头结点的prev指针指向的是尾结点,由于尾结点的更新,head结点的prev指针就得改成newnode。
需要注意的是,为充分利用循环链表的特性,我们修改的时候一般传的就是head头结点,所以实际上是这样的:

因为这种特性,所以我们修改链表结点指针的时候一般是先去修改newnode的指针,再去修改原链表的指针,否则就会这样:
phead->prev = newnode;
请问这样以后,你该怎么找到原链表的phead->prev呢?
因此,之后的操作基本都是先修改newnode的指针,再去修改原链表里的指针:

而且注意到,因为还需要该原链表的尾结点的next指针,所以phead->prev放到最后。
双向链表的遍历打印
另,为方便测试,我们再写一个Print方法,遍历打印整个链表元素:
需要注意的点就是遍历完整个链表的条件可不再是碰到NULL。

开头就应该在head->next
每次循环先打印再往后走,直到......
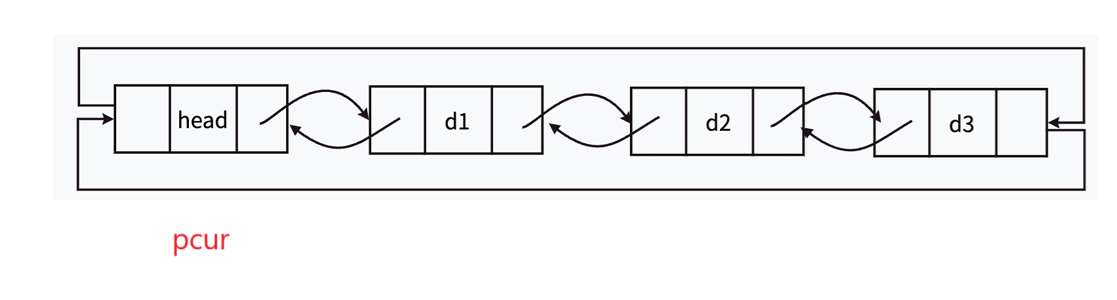
如果遍历链表的指针变为head,说明链表遍历完成了,应该停手了,这也就照应了上面说的"哨兵位"。

测试尾插及遍历打印方法:

双向链表的头插
还是画图看看指针该怎么改:

找到了需要修改的结点:

测试代码:

5.双向链表的删除操作
双向链表的尾删

不多bb,红色的del结点就是要删除的尾结点,绿色的为删除后需要修改的结点。
另外创造了个del结点有俩作用:
①写phead ->prev->prev太难看了有点。
②我们肯定是先修改指针方向,最后再free del整个结点。

但是却漏掉了一个问题,只能保证phead传过来的值不为空,但是并不能保证链表不为空(只有头结点无有效结点就视为空)。
判断链表是否为空
所以应该写一段代码,判断链表不为空:

故修改尾删的assert断言:

不过不要犯糊涂,assert断言也是判断表达式是否为假,而如果链表为空返回true,我们想让他为false,这样才能为空时断言报错。
另外就是Empty这个函数已经验过phead了,没必要再写。
测试代码:

且无有效结点时断言报错:

双向链表的头删
道理基本一样,只不过需要修改的指针得分析分析:

直接给出代码了:

测试代码:


6.双向链表的查找操作
大概想一想,就是遍历整个链表,找到了就返回指定位置,如果都遍历到头结点了,那说明整个链表都没有要找到结点,直接返回NULL就行:

测试代码:


7.双向链表指定位置的插入和删除操作
基于Find方法,可以做到指定位置的插入和删除。
指定位置的插入
指定位置前的插入

依旧画图。
代码实现即可:

测试代码

指定位置后的插入

代码实现:

测试代码:

指定位置的删除

代码实现:

测试代码:

三、线性表和链表对比
学过双向链表以后,体会到的最最舒服的就是不管什么位置的插入和删除都十分简单,不再是让人从头遍历到尾,或者一个一个搬运。
再次重申:如果要让数据连续存储,那就用线性表;内存无要求,只为操作简便,那就用链表(或者说双向链表)。