一、堆中两个重要的算法
我们前面学习了树的概念和结构，还要树的一种特殊树--二叉树，然后我们学习了堆，知道了堆分为大堆和小堆，接下来我们就使用堆来进行一个排序。
在学习我们的堆排序前，我们先详细学习一下我们堆中两个重要的算法：
1、向上调整算法
我们前面在实现堆的插入功能的时候，有简单的讲过这个算法，其在插入操作中，我们所插入的元素是可能会破坏我们的堆的有序结构的，导致我们的二叉树不成堆，这个算法是用来保证我们的堆结构的。
其具体过程如下：
其代码如下:
2、向下调整法
这个算法我们在删除堆顶数据的时候使用的，我们在删除堆顶的元素的时候，对于谁来做这个堆顶是比较难弄的。我们最后就是将原来堆顶的元素和堆尾的元素进行交换，然后删除堆尾，然后我们对当前堆顶的元素进行向下调整。
算法的过程如下：
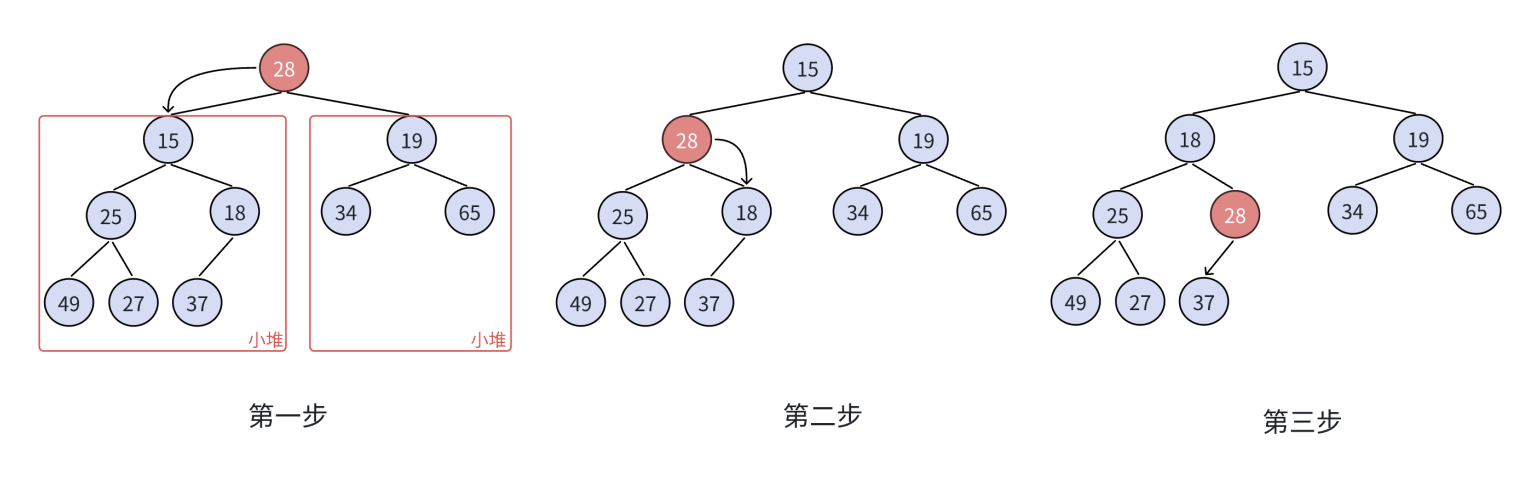
代码如下：
3、两个算法的时间复杂度
首先二叉树有个性质：
我们以一个满二叉树来举例：
向上调整算法：
第1层，2的0次方 个结点，需要向上移动0层，第二层2的一次方个结点，需要向上移动一层，以此类推第h层，有2的h-1个结点，需要向上移动h-1层。
那么我们总的要移动的次数为：
将其换成n：
这个算法和输入的结点的个数的关系，这个就是我们的向上调整算法的时间复杂度。
向下调整算法：
第一层，一个结点，需要向下移动h-1次，第二层，2的一次方个结点，需要向下移动h-2次，依次类推，第h层，2的h-1次方个结点，需要向下移动0次，那么其时间复杂度如下：
将其换成n ：
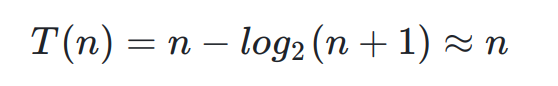
我们可以看到向下调整算法的时间复杂度要比向上调整算法的时间复杂度要低，那么这是为啥呢？
我们可以发现，我们的向下调整算法中，当结点少的时候，其要走的次数要多，，其结点多的时候，要调整的次数少，而反观向上调整算法中，当结点少的时候，其次数少，然后结点多起来的时候其要走的次数就多了，所以他的算法时间复杂度肯定要高过向下调整算法的。
所以我们在接下来的堆排序中使用的更多的是向下调整算法。
二、堆的应用
1、堆排序
根据给的一个数组，将其变成我们的有序的堆结构。
那么我们要如何进行操作，例如我们现在要将这个数组实现升序的结构，那么我们是建大堆还是小堆呢？如果是降序呢？我们又要建大堆还是小堆呢？
我们如果是要是实现升序，那么我们建一个大堆，然后将堆顶的元素变成数组的前面的元素，然后将堆顶的元素和堆尾的元素进行交换，然后将此时的堆尾的元素进行删除，然后再对这个堆向下调整，反复操作，知道将数组变成升序的。
其就是先将堆顶元素取到，然后再进行删除堆顶元素。
不过上述的方法就需要我们先将现在的数组变成堆的结构。那么我们就将数组的元素一个一个的入堆即可。
那么要是要实现降序，那么我们就建小堆，后续的操作还是一样的。
代码如下：
2、TOK-K问题
TOK-K问题：即求数据集合中的前k个最大的元素，或者最小的元素，其在我们的生活中是非常常见的，比如说我们的福布斯富豪榜，五一小黄金周热门出现城市，流入人口最多的几个城市等等，这种问题一般情况下，数据量都会比较大，那么对于这种问题，没有任何限制的情况下，我们肯定最先想到的是排序，如果数据量非常非常非常大，那么排序方法就不可取了，那么我们要咋办呢？
比如说现在我们有4个G 的数据需要进行比较，但是我们只有1G的内存，所以是没办法将全部数据都存储起来的，那么我们要怎么办呢？
我们可以将这4G个数据，我们先取1G，然后我们使用我们的堆数据结构。如果我们是要取的是前K个最大的数据，那么我们就建小堆，然后我们再遍历剩下的3G的数据，然后将其与堆顶的元素进行比较，如果其比堆顶的元素大，那么我们就将堆顶的元素换掉，然后再使用向下调整法，如此反复。自此，完成后，这个堆中的K个元素就是这4G中的大的K个元素。
反之如果我们是要找前K个小的元素，那么我们就需要建大堆了，然后遍历剩下的数据，如果其比堆顶要小，那么就将堆顶换掉，然后使用向下调整法。
代码如下：
以上就是我们的堆的应用部分的内容了，谢谢大家的观看。