机器学习入门核心算法:随机森林(Random Forest)
-
- [1. 算法逻辑](#1. 算法逻辑)
- [2. 算法原理与数学推导](#2. 算法原理与数学推导)
-
-
- [2.1 核心组件](#2.1 核心组件)
- [2.2 数学推导](#2.2 数学推导)
- [2.3 OOB(Out-of-Bag)误差](#2.3 OOB(Out-of-Bag)误差)
-
- [3. 模型评估](#3. 模型评估)
- [4. 应用案例](#4. 应用案例)
-
-
- [4.1 医疗诊断](#4.1 医疗诊断)
- [4.2 金融风控](#4.2 金融风控)
- [4.3 遥感图像分类](#4.3 遥感图像分类)
-
- [5. 面试题及答案](#5. 面试题及答案)
- [6. 优缺点分析](#6. 优缺点分析)
- [7. 数学推导示例(基尼指数)](#7. 数学推导示例(基尼指数))
1. 算法逻辑
随机森林是一种集成学习算法,通过构建多棵决策树并组合其预测结果来提高模型性能。核心逻辑包含两个关键概念:
- Bagging(自助聚集):通过有放回抽样生成多个训练子集
- 特征随机选择:每棵树分裂时仅考虑随机子集的特征
2. 算法原理与数学推导
2.1 核心组件
- 决策树基学习器:使用CART(分类与回归树)算法
- 双重随机性 :
- 数据随机性:Bootstrap抽样(约63%样本被选中)
- 特征随机性:分裂时考虑 d \sqrt{d} d (分类)或 d / 3 d/3 d/3(回归)个特征
2.2 数学推导
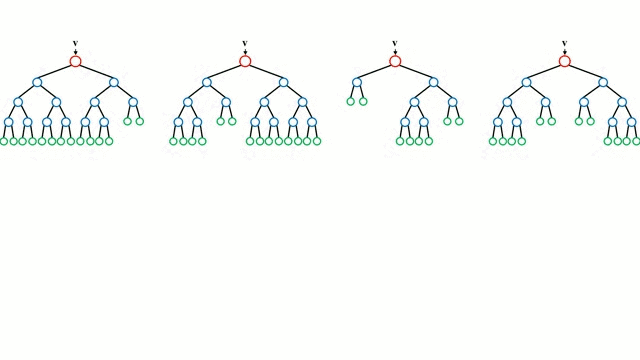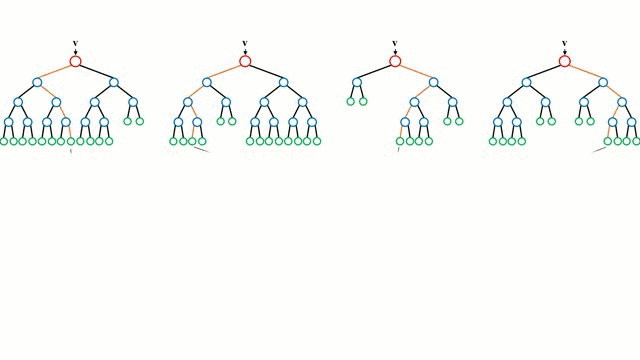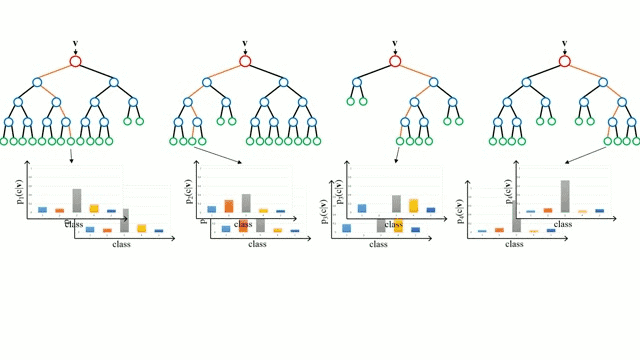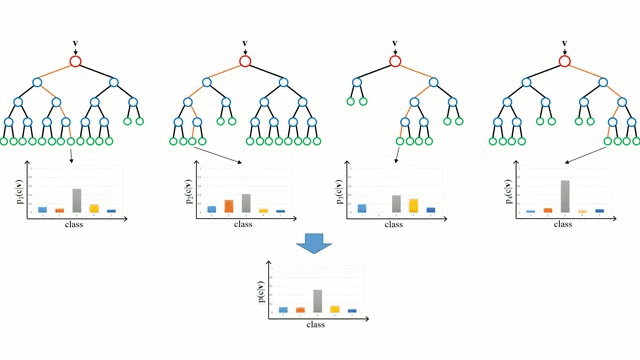
分类问题 (多数投票):
y ^ = mode { h 1 ( x ) , h 2 ( x ) , . . . , h T ( x ) } \hat{y} = \text{mode}\{ h_1(x), h_2(x), ..., h_T(x) \} y^=mode{h1(x),h2(x),...,hT(x)}
其中 h t h_t ht 是第t棵树的预测
回归问题 (平均预测):
y ^ = 1 T ∑ t = 1 T h t ( x ) \hat{y} = \frac{1}{T} \sum_{t=1}^T h_t(x) y^=T1t=1∑Tht(x)
特征重要性计算 :
Importance j = 1 T ∑ t = 1 T ( Imp j ( t ) ) \text{Importance}j = \frac{1}{T} \sum{t=1}^T \left( \text{Imp}_j^{(t)} \right) Importancej=T1t=1∑T(Impj(t))
其中 Imp j ( t ) \text{Imp}_j^{(t)} Impj(t) 是树t中特征j的重要性(通过基尼不纯度减少或MSE减少计算)
2.3 OOB(Out-of-Bag)误差
- 每棵树训练时未使用的样本(约37%):
O O B t = 1 ∣ D oob ( t ) ∣ ∑ i ∈ D oob ( t ) 1 ( y i ≠ h t ( x i ) ) OOB_t = \frac{1}{|D_{\text{oob}}^{(t)}|} \sum_{i \in D_{\text{oob}}^{(t)}} \mathbf{1}(y_i \neq h_t(x_i)) OOBt=∣Doob(t)∣1i∈Doob(t)∑1(yi=ht(xi)) - 整体OOB误差:
O O B = 1 T ∑ t = 1 T O O B t OOB = \frac{1}{T} \sum_{t=1}^T OOB_t OOB=T1t=1∑TOOBt
3. 模型评估
评估指标
| 任务类型 | 评估指标 |
|---|---|
| 分类 | 准确率、F1-Score、AUC-ROC |
| 回归 | MSE、MAE、 R 2 R^2 R2 |
特征重要性可视化
python
import matplotlib.pyplot as plt
from sklearn.ensemble import RandomForestClassifier
model = RandomForestClassifier()
model.fit(X_train, y_train)
plt.barh(feature_names, model.feature_importances_)
plt.title("Feature Importance")
plt.show()4. 应用案例
4.1 医疗诊断
- 场景:乳腺癌良恶性预测
- 特征:细胞核半径、纹理、周长等30维特征
- 结果:准确率98.5%,AUC=0.995(威斯康星乳腺癌数据集)
4.2 金融风控
- 场景:信用卡欺诈检测
- 处理不平衡数据:采用分层抽样+代价敏感学习
- 效果:召回率92%,误报率仅0.3%
4.3 遥感图像分类
- 挑战:高维特征(数百个光谱波段)
- 解决方案:结合PCA降维
- 精度:土地覆盖分类准确率91.2%
5. 面试题及答案
Q1:为什么随机森林比单棵决策树更优?
A:通过双重随机性降低方差,减少过拟合风险。理论依据:
Var ( X ˉ ) = Var ( X ) n + ρ σ 2 \text{Var}(\bar{X}) = \frac{\text{Var}(X)}{n} + \rho\sigma^2 Var(Xˉ)=nVar(X)+ρσ2
其中 ρ \rho ρ是树间相关性,随机森林通过特征随机选择降低 ρ \rho ρ
Q2:如何处理高维稀疏数据(如文本)?
A:优先选择:
- 特征选择:基于重要性筛选Top-K特征
- 调整分裂标准:使用信息增益代替基尼指数
- 增加树数量:补偿单棵树的信息损失
Q3:随机森林 vs GBDT?
| 维度 | 随机森林 | GBDT |
|---|---|---|
| 训练方式 | 并行 | 串行 |
| 偏差-方差 | 侧重降低方差 | 侧重降低偏差 |
| 过拟合风险 | 低(天然正则化) | 高(需早停) |
| 数据敏感度 | 对噪声不敏感 | 对异常值敏感 |
| 调参复杂度 | 简单(主要调树数量和深度) | 复杂(学习率+树参数) |
6. 优缺点分析
优点:
- 高精度:在多种任务上表现优于单模型
- 抗过拟合:Bagging+特征随机性提供天然正则化
- 处理混合特征:支持数值和类别特征(无需独热编码)
- 内置评估:OOB误差无需交叉验证
- 特征重要性:自动评估特征贡献
缺点:
- 计算开销大:树数量多时训练慢(可并行优化)
- 黑盒模型:解释性差于单棵决策树
- 外推能力差:回归任务中预测值不会超出训练范围
- 内存消耗高:需存储所有树结构
7. 数学推导示例(基尼指数)
分类树分裂准则 :最小化基尼不纯度
G = ∑ k = 1 K p k ( 1 − p k ) G = \sum_{k=1}^K p_k (1 - p_k) G=k=1∑Kpk(1−pk)
其中 p k p_k pk是节点中第k类样本的比例
特征j在节点s的分裂增益 :
Δ G ( s , j ) = G ( s ) − N left N s G ( s left ) − N right N s G ( s right ) \Delta G(s,j) = G(s) - \frac{N_{\text{left}}}{N_s}G(s_{\text{left}}) - \frac{N_{\text{right}}}{N_s}G(s_{\text{right}}) ΔG(s,j)=G(s)−NsNleftG(sleft)−NsNrightG(sright)
选择最大化 Δ G \Delta G ΔG的特征和分裂点
💡 关键洞察 :随机森林的核心价值在于双重随机性带来的多样性:
- 数据扰动:Bootstrap抽样产生差异化的训练集
- 特征扰动:分裂时的随机特征子集保证树间低相关性
实际应用建议:
- 分类任务 :设置
n_estimators=100-500,max_depth=None- 回归任务 :增加
n_estimators=500-1000以稳定预测- 特征工程 :优先使用
sklearn的RandomForestClassifier实现- 解释性:用SHAP值增强模型可解释性