数据结构算法题：list

链表

一.排队序列
二.单向链表
三.队列安排
- 1.题目
- 2.解题思路
- - [2.1 圈出关键字眼](#2.1 圈出关键字眼)
  - [2.2 解题思路推导](#2.2 解题思路推导)
  - - [(1) 数据结构设计](#(1) 数据结构设计)
    - [(2) 初始化逻辑](#(2) 初始化逻辑)
    - (3)插入操作（左/右插入）
    - (4)删除操作
    - [(5) 遍历输出](#(5) 遍历输出)
  - 2.3代码与思路的对应
- 3.参考代码
四.约瑟夫问题
- 1.题目
- 2.解题思路
- - [2.1. 问题分析](#2.1. 问题分析)
  - [2.2 数据结构选择](#2.2 数据结构选择)
  - [2.3 核心思路](#2.3 核心思路)
  - [2.4 具体步骤](#2.4 具体步骤)
- 3.参考代码
- - 代码复杂度分析

一.排队序列

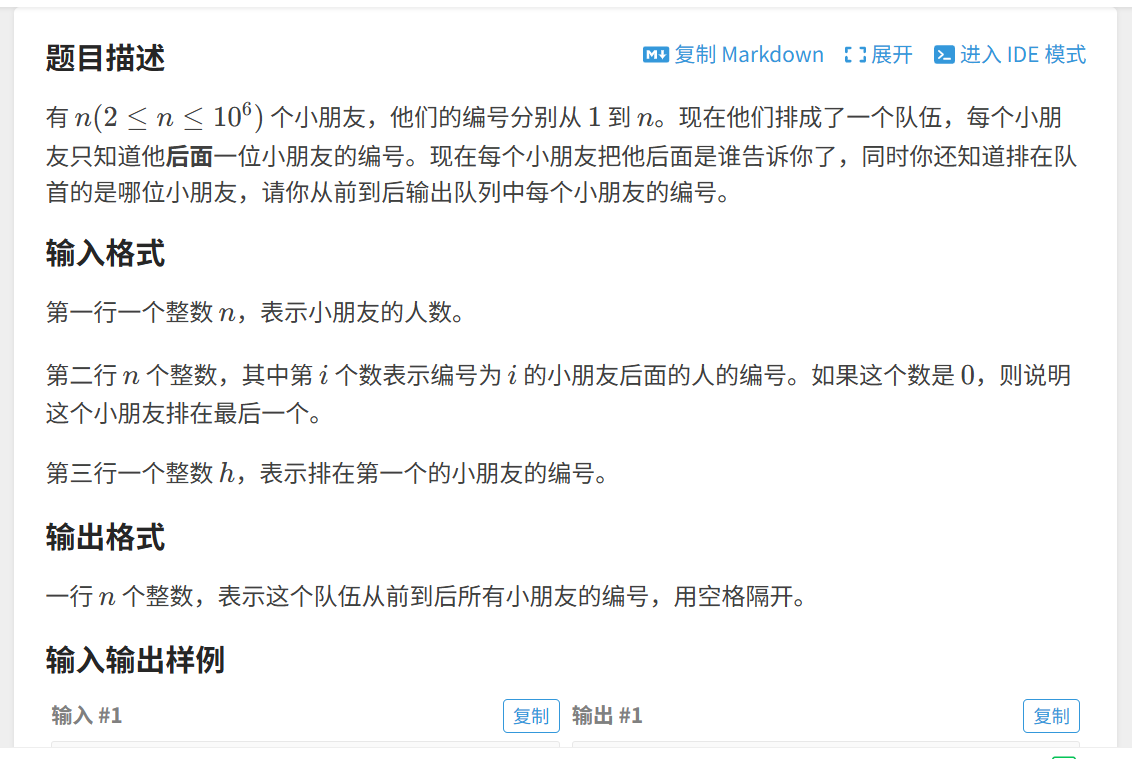
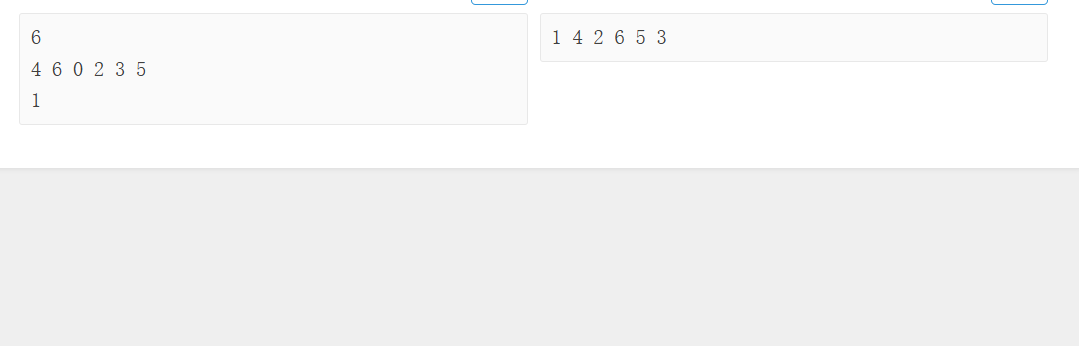
1.题目

2.解题思路

本题的解题思路基于单链表的遍历，核心是利用"每个小朋友只知道后面一位编号"的条件，通过数组模拟链表的后继关系，从队首开始依次遍历输出。

步骤1：理解数据结构

题目中每个小朋友的"后面是谁"可以用数组 ne 来存储，其中 ne[i] 表示编号为 i 的小朋友后面的人的编号。当 ne[i] = 0 时，表示该小朋友是队尾。

步骤2：输入处理

首先输入小朋友的人数 n。
接着输入 n 个整数，存入数组 ne，其中 ne[i] 对应编号为 i 的小朋友的后继。
最后输入队首小朋友的编号 h。

步骤3：遍历输出

从队首 h 开始，依次访问当前小朋友的后继（即 ne[i]），直到遇到 0（队尾）为止，期间依次输出每个小朋友的编号。

本方法的时间复杂度是 O(n) （仅需遍历每个小朋友一次），空间复杂度是 O(n) （需要一个数组存储后继关系），完全满足题目中 n ≤ 10^6 的数据规模要求。

3.参考代码

cpp 复制代码

#include <iostream>
using namespace std;

const int N = 1e6 + 10; // 数组大小略大于数据范围，避免越界
int ne[N];//存储第二行的数据

int main() {
    int n;//定义n,即输入元素个数
    cin >> n;
    if (n == 0) return 1;
    for (int i = 1; i <= n; i++) { 
        cin >> ne[i];
    }
    int h;//定义h接收第一个元素
    cin >> h;
    for (int i = h; i; i = ne[i]) {
        cout << i << " ";
    }
    return 0;
}

二.单向链表

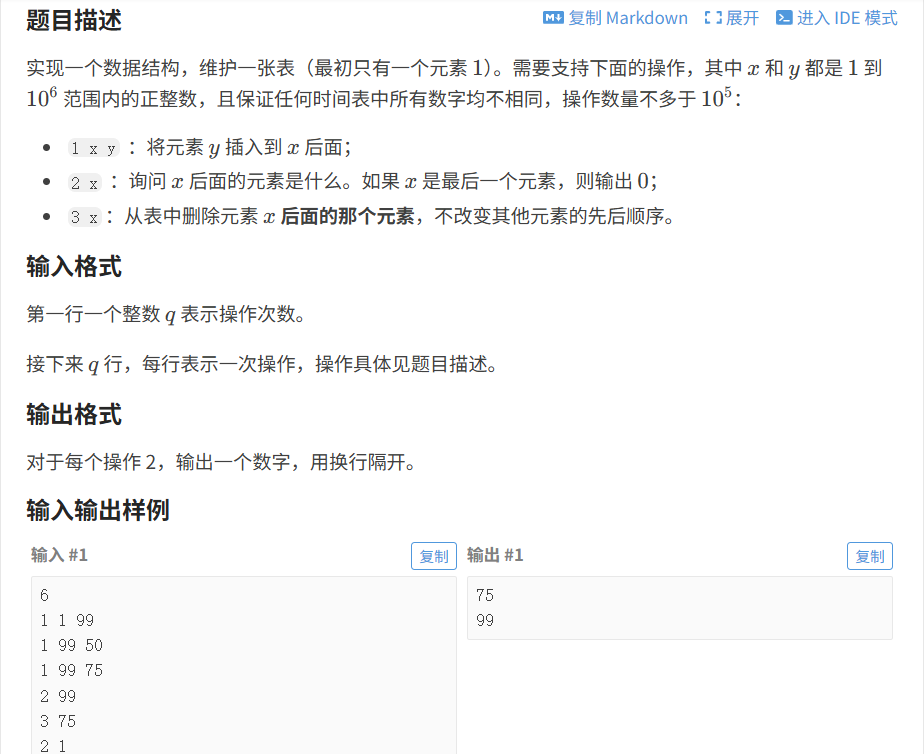
1.题目

2.解题思路

要解决以上题目，我们需要实现一个支持快速插入、查询和删除 操作的数据结构。由于操作次数和数据范围较大（最多 (10^5) 次操作，元素值到 (10^6)），普通数组的插入/删除效率不足，因此采用数组模拟单链表的方式，结合哈希映射实现高效操作。

2.1具体步骤

数据结构选择：数组模拟单链表 + 哈希映射
- 用三个数组分别存储：
  - e[N]：存储节点的值（每个节点对应一个元素）。
  - ne[N]：存储节点的"后继指针"（即下一个节点的索引）。
  - mp[M]：哈希映射，将元素值映射到其在链表中的节点索引（实现"值→节点"的快速查找）。
- 用 id 作为节点索引的计数器，管理节点的分配。
核心操作实现
- 插入操作（类型1） ：在元素 x 后插入 y。通过 mp[x] 找到 x 的节点索引 p，分配新节点存储 y，并调整指针关系（新节点的后继指向 x 的原后继，x 的后继指向新节点）。
- 查询操作（类型2） ：查询 x 后面的元素。通过 mp[x] 找到 x 的节点索引 p，输出其"后继节点"的值；若后继为空（索引为0），则输出0。
- 删除操作（类型3） ：删除 x 后面的元素。通过 mp[x] 找到 x 的节点索引 p，直接跳过待删除节点（让 x 的后继指向"待删除节点的后继"）。
边界处理
- 初始链表只有元素 1，需特殊初始化其节点索引和指针。
- 若元素 x 不存在（mp[x] == 0 且 x != 1），则跳过无效操作，保证程序健壮性。

2.2复杂度分析

时间复杂度：所有操作（插入、查询、删除）的时间复杂度均为 (O(1))，因为通过哈希映射和数组直接访问，无需遍历链表。
空间复杂度：(O(N + M))，其中 (N) 是节点最大数量（(10^5 + 10)），(M) 是元素值的最大范围（(10^6 + 10)），可满足题目约束。

3.参考代码

cpp 复制代码

#include <iostream>
using namespace std;

// N: 链表节点最大数量，M: 元素值的最大范围（用于映射）
const int N = 1e5 + 10, M = 1e6 + 10;
int id;               // 节点索引计数器（全局变量，初始值0）
int e[N];             // 存储节点值（e[i]表示索引i的节点值）
int ne[N];            // 存储节点的next指针（ne[i]表示索引i的下一个节点索引）
int mp[M];            // 映射表：mp[val] = i 表示值为val的节点索引是i


int main()
{
    // 初始化：创建第一个节点（值为1）
    e[id] = 1;       // 初始节点索引为0，值为1
    mp[1] = id;      // 记录值1对应的节点索引（0）
    ne[id] = 0;      // 初始节点的next指针为空（0表示空）

    int x = 0, q, sign;
    cin >> q;        // 读取操作次数
    while (q--)
    {
        cin >> sign >> x;  // sign：操作类型（1插入/2查询/3删除），x：目标元素
        int p = mp[x];     // 获取x对应的节点索引p

        // 检查x是否存在（p=0表示x不存在，因为有效节点索引从0开始，后续新增从1起）
        if (p == 0 && x != 1) {  // 特殊处理初始节点1（其索引为0）
            continue;  // x不存在，跳过本次操作
        }

        if (sign == 1)  // 操作1：在x后面插入y
        {
            int y; cin >> y;
            e[++id] = y;  // 分配新节点，值为y（id自增，新索引从1开始）
            
            // 插入逻辑：新节点的next指向x的next，x的next指向新节点
            ne[id] = ne[p];
            ne[p] = id;
            mp[y] = id;  // 记录y对应的节点索引（新节点id）
        }
        else if (sign == 2)  // 操作2：查询x后面的元素
        {
            // 输出x的next节点的值（若next为空，e[0]为0）
            cout << e[ne[p]] << endl;
        }
        else  // 操作3：删除x后面的元素
        {
            // 跳过x的next节点（让x的next指向next的next）
            ne[p] = ne[ne[p]];
        }
    }
    return 0;
}

三.队列安排

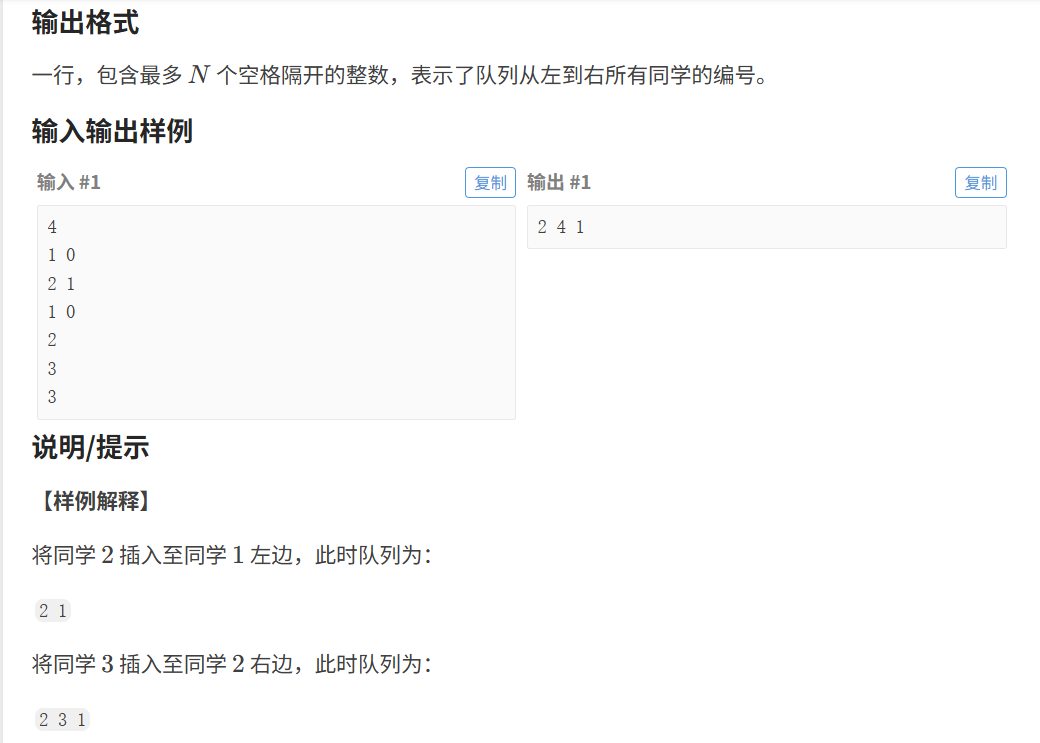
1.题目

2.解题思路

要解决这个问题，我们首先需要圈出关键字眼。

2.1 圈出关键字眼

核心操作 ：插入（左/右） 、删除、遍历输出
数据结构 ：双向循环链表 （支持左右插入、前驱/后继指针）、哈希映射（快速通过值找节点）
约束条件：(1 \leq N \leq 10^6)、操作数 (M \leq 10^6)、元素唯一

2.2 解题思路推导

基于关键字眼和题目要求，采用**"双向循环链表 + 哈希映射"**的方案，保证插入、删除、遍历的高效性：

(1) 数据结构设计

双向循环链表 ：用数组 e[] 存节点值，pre[] 存前驱指针，ne[] 存后继指针，h 作为头节点（索引固定为0）。
哈希映射 mp[] ：将"同学编号"映射到链表节点的索引，实现 O(1) 时间定位节点。
节点计数器 id：管理节点的唯一索引分配。

(2) 初始化逻辑

初始队列只有同学 1：

节点索引从 1 开始分配，e[1] = 1 存储值。
mp[1] = 1 记录编号 1 对应的节点索引。
头节点 h=0 的前驱和后继均指向节点 1，节点 1 的前驱和后继均指向头节点，形成循环链表。

(3)插入操作（左/右插入）

左插入（sign==1） ：在同学 x 的左边插入新同学 i。
- 通过 mp[x] 找到 x 的节点索引 p。
- 分配新节点 id++，存储 i 并记录映射 mp[i] = id。
- 调整指针：新节点的后继指向 p，前驱指向 p 的原前驱；p 的原前驱的后继指向新节点，p 的前驱指向新节点。
右插入（sign==0） ：在同学 x 的右边插入新同学 i。
- 通过 mp[x] 找到 x 的节点索引 p。
- 分配新节点 id++，存储 i 并记录映射 mp[i] = id。
- 调整指针：新节点的前驱指向 p，后继指向 p 的原后继；p 的原后继的前驱指向新节点，p 的后继指向新节点。

(4)删除操作

删除指定同学 x：

通过 mp[x] 找到 x 的节点索引 p。
调整指针：跳过节点 p，让 p 的前驱的后继指向 p 的后继，p 的后继的前驱指向 p 的前驱。
清除映射 mp[x] = 0，标记 x 已被删除。

(5) 遍历输出

从头节点的后继 开始遍历，直到遇到空指针（循环链表中头节点的后继最终会回到头节点，所以遍历条件为 j != h），依次输出节点值。

2.3代码与思路的对应

数组 e[]、pre[]、ne[] 实现双向循环链表的节点存储和指针关系。
mp[] 实现"值→节点索引"的快速映射，保证插入/删除时能 O(1) 定位节点。
插入时的指针调整逻辑严格遵循"左插入"和"右插入"的定义，删除时的指针调整保证链表连续性，遍历输出则按"从左到右"的顺序输出有效节点。

该解题思路通过双向循环链表 支持左右插入的灵活性，哈希映射保证节点定位的高效性，最终满足题目中 (10^6) 级别的数据规模和操作次数要求。

3.参考代码

cpp 复制代码

```cpp
#include<iostream>
using namespace std;

const int N = 1e5 + 10;
// h: 头节点索引(固定为0，不存储实际值)
// id: 节点计数器(从1开始分配有效节点)
// e[N]: 存储节点值（同学编号）
// pre[N]: 存储前驱节点索引
// ne[N]: 存储后继节点索引
// mp[N]: 哈希映射，同学编号→节点索引
int h, id, e[N], pre[N], ne[N], mp[N];  

int main()
{
    h = 0;  // 初始化头节点索引为0
    id = 1;  // 第一个有效节点索引从1开始
    e[id] = 1;  // 初始同学编号为1
    mp[1] = id;  // 记录编号1对应的节点索引
    pre[id] = h;  // 节点1的前驱是头节点
    ne[id] = h;  // 节点1的后继是头节点
    pre[h] = id;  // 头节点的前驱是节点1
    ne[h] = id;  // 头节点的后继是节点1

    int n, m, sign, x;
    cin >> n;  // 总同学数（包含初始的1）
    for (int i = 2; i <= n; i++)  // 插入同学2~n（共n-1个）
    {
        cin >> x >> sign;
        int p = mp[x];  // 获取同学x对应的节点索引
        if (!sign )  // sign==1：在x的左边插入i
        {
            e[++id] = i;  // 分配新节点，存储同学i
            mp[i] = id;   // 记录同学i的节点索引

            // 指针调整：新节点的后继指向x，前驱指向x的原前驱
            ne[id] = p;
            pre[id] = pre[p];
            // x的原前驱的后继指向新节点，x的前驱指向新节点
            ne[pre[p]] = id;
            pre[p] = id;
        }
        else  // sign==0：在x的右边插入i
        {
            e[++id] = i;  // 分配新节点，存储同学i
            mp[i] = id;   // 记录同学i的节点索引

            // 指针调整：新节点的前驱指向x，后继指向x的原后继
            pre[id] = p;
            ne[id] = ne[p];
            // x的原后继的前驱指向新节点，x的后继指向新节点
            pre[ne[p]] = id;
            ne[p] = id;
        }
    }
    cin >> m;  // 要删除的同学数量
    while (m--)
    {
        cin >> x;
        if (mp[x] == 0) continue;  // 同学x不存在，跳过操作
        int p = mp[x];  // 获取同学x的节点索引
        // 指针调整：跳过节点p，连接其前驱和后继
        ne[pre[p]] = ne[p];
        pre[ne[p]] = pre[p];
        mp[x] = 0;  // 标记同学x已被删除
    }
    // 从头节点的后继开始遍历，输出所有有效同学
    for (int j = ne[h]; j; j = ne[j])
        cout << e[j] << " ";
    return 0;
}

四.约瑟夫问题

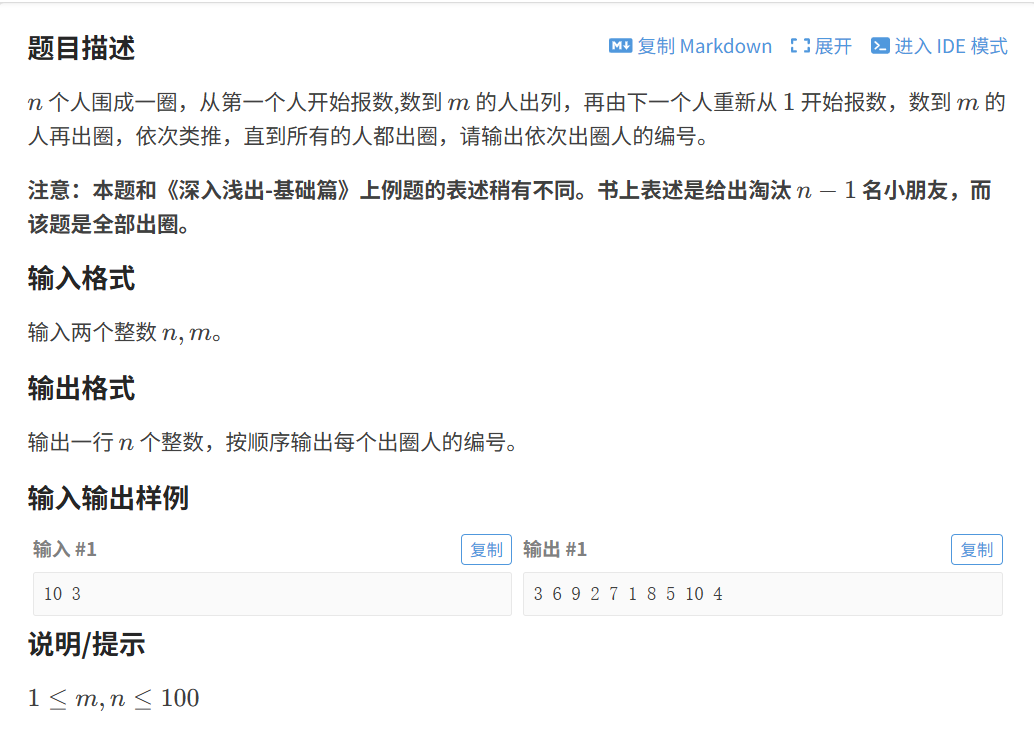
1.题目

2.解题思路

要解决这道约瑟夫环问题，我们可以通过模拟报数出圈过程 结合迭代器优化来实现。

2.1. 问题分析

题目要求模拟 n 个人围成一圈报数，数到 m 的人出圈，直到所有人都出圈，并输出出圈顺序。核心是模拟"循环报数-出圈"的过程，需解决循环遍历 和元素删除后迭代器失效的问题。

2.2 数据结构选择

使用 list（双向链表）来存储人员编号，因为它的插入、删除操作时间复杂度为 O(1) （配合迭代器），适合模拟"出圈"操作；同时链表的循环遍历特性也能很好地模拟"围成一圈"的场景。

2.3 核心思路

初始化 ：用 list 存储 1~n 的编号，模拟 n 个人围成一圈。
循环报数与出圈 ：
- 维护一个迭代器 it 来跟踪当前报数的位置。
- 有效移动步数优化 ：通过 (m-1) % s（s 为当前环的大小）统一处理 m 和 n 的大小关系，将有效移动步数限制在 [0, s-1] 范围内，避免无效循环：
  - 若 m > n：例如 n=5，m=100，初始 s=5 时，(100-1)%5 = 4，只需移动 4 步而非 99 步，大幅减少无效绕圈。
  - 若 m == n：例如 n=5，m=5，(5-1)%5 = 4，移动 4 步后定位到当前环最后一个元素，符合报数逻辑。
  - 若 m < n：例如 n=10，m=3，(3-1)%10 = 2，直接移动 m-1 步即可准确定位。
- 移动迭代器到目标位置后，输出当前编号并删除该元素（利用 list::erase() 的返回值更新迭代器，避免失效）。
- 若迭代器到达链表末尾，重置为开头，保证"围成一圈"的循环逻辑。

2.4 具体步骤

初始化链表 ：将 1~n 依次加入 list 中。
循环处理直到链表为空 ：
- 计算当前环的大小 s = lt.size()。
- 计算有效移动步数 step = (m - 1) % s（核心优化，覆盖 m 和 n 所有大小关系）。
- 移动迭代器 step 步，定位到要出圈的人。
- 输出该编号，删除该元素（通过 erase() 的返回值更新迭代器）。
- 若迭代器到末尾，重置为开头，继续循环。

3.参考代码

cpp 复制代码

#include<iostream>
#include<list>
using namespace std;

int main() {
    int n, m;
    cin >> n >> m;
    list<int> lt;
    for (int i = 1; i <= n; ++i) {
        lt.push_back(i);
    }
    auto it = lt.begin();
    while (!lt.empty()) {
        int s = lt.size();
        int step = (m - 1) % s; // 计算有效移动步数，统一处理m和n的大小关系
        
        // 移动step步定位到出圈元素
        for (int i = 0; i < step; ++i) {
            ++it;
            if (it == lt.end()) {
                it = lt.begin();
            }
        }
        
        // 输出并删除当前元素，更新迭代器
        cout << *it << " ";
        it = lt.erase(it);
        
        // 若迭代器到末尾，重置为开头
        if (it == lt.end()) {
            it = lt.begin();
        }
    }
    return 0;
}

代码复杂度分析

时间复杂度：通过 (m-1) % s 优化后，时间复杂度为 O(n²) （每轮移动步数最多为当前环大小减 1，总步数为 1+2+...+(n-1) ≈ n²/2）。
空间复杂度：O(n) （存储 n 个元素的链表）。

这种解法法在题目给定的约束（1 ≤ m, n ≤ 100）下效率很高，能快速输出所有出圈人的编号。