数据结构与算法学习笔记----动态规划·区间DP
@@ author: 明月清了个风
@@ first publish time: 2025.5.26
ps⭐️区间DP的特征在于子结构一般是一个子区间上的问题,涉及到的问题也非常多,如环形区间,记录方案数,高精度,二维区间等等。这次的题目基本包含了这些知识点的处理方法。
Acwing 1068. 环形石子合并
将 n n n堆石子绕圆形操场摆放,现要将石子有序地合并成一堆。
规定每次只能选相邻的两堆合并成新的一对,并将新的一堆石子堆数记作该次合并的得分。
请编写一个程序,读入堆数 n n n及每堆的石子数,并进行如下计算:
- 选择一种合并石子的方案,使得做 n − 1 n - 1 n−1次合并得分总和最大
- 选择一种合并石子的方案,使得做 n − 1 n - 1 n−1次合并得分总和最小。
输入格式
第一行包含整数 n n n,表示共有 n n n堆石子。
第二行包含 n n n个整数,分别表示每堆石子的数量。
输出格式
输出共两行:
第一行为合并得分的最小值。
第二行为合并得分的最大值。
数据范围
1 ≤ n ≤ 200 1 \le n \le 200 1≤n≤200,
思路
对于环形摆放的 n n n堆石子进行 n − 1 n - 1 n−1次合并,最后一定会有一个缺口,因此第一个思路是枚举这个缺口在哪两个之间,这样就将环形的石子堆变成了正常摆放的,进行最简单的区间DP就行,不过这个时间复杂度会变成 n 4 n^4 n4会超时(枚举缺口 n n n,区间DP是 n 3 n^3 n3)。
可以发现,无论如何合并,最后一定是 n n n个点的连线,只是顺序不一样,因此可以将环形直接展开,并按照顺序向后复制一份,也就是变成 2 n 2n 2n堆石子。要求的合并方案就是在这 2 n 2n 2n个石子中选择长度为 n n n的区间进行合并,这也是环形问题的经典处理方式。
代码
cpp
#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 410, inf = 0x3f3f3f3f;
int n;
int q[N], s[N];
int f[N][N], g[N][N];
int main()
{
cin >> n;
for(int i = 1; i <= n; i ++) cin >> q[i], q[i + n] = q[i];
for(int i = 1; i <= n * 2; i ++) s[i] = s[i - 1] + q[i];
memset(f, 0x3f, sizeof f);
memset(g, -0x3f, sizeof g);
for(int len = 1; len <= n; len ++)
for(int l = 1; l + len - 1 <= n * 2; l ++)
{
int r = l + len - 1;
if(l == r) f[l][r] = g[l][r] = 0;
else
{
for(int k = l; k < r; k ++)
{
f[l][r] = min(f[l][r], f[l][k] + f[k + 1][r] + s[r] - s[l - 1]);
g[l][r] = max(g[l][r], g[l][k] + g[k + 1][r] + s[r] - s[l - 1]);
}
}
}
int maxv = -inf, minv = inf;
for(int i = 1; i <= n; i ++)
{
maxv = max(maxv, g[i][i + n - 1]);
minv = min(minv, f[i][i + n - 1]);
}
cout << minv << endl << maxv << endl;
return 0;
}Acwing 320. 能量项链
在 Mars 星球上,每个 Mars 人都随身佩带着一串能量项链,在项链上有 NN 颗能量珠。
能量珠是一颗有头标记与尾标记的珠子,这些标记对应着某个正整数。
并且,对于相邻的两颗珠子,前一颗珠子的尾标记一定等于后一颗珠子的头标记。
因为只有这样,通过吸盘(吸盘是 Mars 人吸收能量的一种器官)的作用,这两颗珠子才能聚合成一颗珠子,同时释放出可以被吸盘吸收的能量。
如果前一颗能量珠的头标记为 m m m,尾标记为 r r r,后一颗能量珠的头标记为 r r r,尾标记为 n n n,则聚合后释放的能量为 m × r × n m \times r \times n m×r×n,新产生的珠子头标记为 m m m,尾标记为 n n n。
需要时,Mars 人就用吸盘夹住相邻的两颗珠子,通过聚合得到能量,直到项链上只剩下一颗珠子为止。
显然,不同的聚合顺序得到的总能量是不同的,请你设计一个聚合顺序,使一串项链释放出的总能量最大。
例如:设 N = 4 N = 4 N=4, 4 4 4颗珠子的头标记与尾标记依次为 ( 2 , 3 ) ( 3 , 5 ) ( 5 , 10 ) ( 10 , 2 ) (2,3)(3,5)(5,10)(10,2) (2,3)(3,5)(5,10)(10,2)。
我们用记号 ⊕ 表示两颗珠子的聚合操作, 表示两颗珠子的聚合操作, 表示两颗珠子的聚合操作,(j⊕k) 表示第 表示第 表示第 j,k两颗珠子聚合后所释放的能量。则
第 4、14、1 两颗珠子聚合后释放的能量为: ( 4 ⊕ 1 ) = 10 × 2 × 3 = 60 (4⊕1)=10×2×3=60 (4⊕1)=10×2×3=60。
这一串项链可以得到最优值的一个聚合顺序所释放的总能量为 ((4⊕1)⊕2)⊕3)=10×2×3+10×3×5+10×5×10=710
输入格式
输入的第一行是一个正整数 N N N,表示项链上珠子的个数。
第二行是 N N N个用空格隔开的正整数,所有的数均布超过 1000 1000 1000,第 i i i个数为第 i i i颗珠子的头标记,当 i < N i < N i<N时,第 i i i颗珠子的尾标记应该等于第 i + 1 i + 1 i+1颗珠子的头标记,第 N N N颗坠子的尾标记应该等于第 1 1 1颗珠子的头标记。
至于珠子的顺序,你可以这样确定:将项链放到桌面上,不要出现交叉,随意指定第一颗珠子,然后按顺时针方向确定其他珠子的顺序。
输出格式
输出只有一行,是一个正整数 E,为一个最优聚合顺序所释放的总能量。
数据范围
4 ≤ N ≤ 100 4 \le N \le 100 4≤N≤100,
1 ≤ E ≤ 2.1 × 10 9 1 \le E \le 2.1 \times 10^9 1≤E≤2.1×109
思路
很明显这也是一个环形区间DP问题,可以和上一题一样展开进行计算,只需考虑链式如何计算。
首先是状态的化简,对于 2 , 3 , 5 , 10 2,3,5,10 2,3,5,10表示的 4 4 4颗珠子可以使用 2 , 3 , 5 , 10 , 2 2,3,5,10,2 2,3,5,10,2五个数完全表示,对于状态表示,使用 f [ l ] [ r ] f[l][r] f[l][r]表示所有将 ( l , r ) (l, r) (l,r)这一段合并后的方式,属性是最大值。对于 2 , 3 , 5 , 10 2,3,5,10 2,3,5,10来说,答案就是 f [ 1 ] [ 5 ] f[1][5] f[1][5],因为最后是由五个数完全表示的。
对于状态转移,考虑最后一步的操作,也就是 ( l , r ) (l,r) (l,r)中的分界点 k k k划分为 f [ l ] [ k ] f[l][k] f[l][k]与 f [ k ] [ r ] f[k][r] f[k][r]。需要注意的是,这里是 f [ k ] [ r ] f[k][r] f[k][r],而不是上一题中的 f [ k + 1 ] [ r ] f[k + 1][r] f[k+1][r],因为在这一题中,每个参与合并的珠子要两个数进行表示,因此第 k k k个数是前后共用的。
同样地,我们枚举区间长度 l e n len len的时候需要枚举至长度为 n + 1 n + 1 n+1的区间。
代码
cpp
#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 210;
int n;
int w[N];
int f[N][N];
int main()
{
cin >> n;
for(int i = 1; i <= n; i ++) cin >> w[i], w[i + n] = w[i];
for(int len = 1; len <= n + 1; len ++)
for(int l = 1; l + len - 1 <= n * 2; l ++)
{
int r = l + len - 1;
if(l == r && l + 1 == r) f[l][r] = 0;
else
{
for(int k = l + 1; k < r; k ++)
f[l][r] = max(f[l][r], f[l][k] + f[k][r] + w[l] * w[k] * w[r]);
}
}
int maxv = -1;
for(int i = 1; i <= n; i ++)
maxv = max(maxv, f[i][i + n]);
cout << maxv << endl;
return 0;
}Acwing 1069. 凸多边形的划分
给定一个具有 N N N个顶点的凸多边形,将顶点从 1 1 1到 N N N标号,每个顶点的权值都是一个正整数。
将这个凸多边形划分成 N − 2 N - 2 N−2个互不相交的三角形,对于每个三角形,其三个顶点的权值相乘都可得到一个权值乘积,试求所欲三角形的顶点权值乘积之和至少为多少。
输入格式
第一行包含整数 N N N,表示顶点数量。
第二行包含 N N N个整数,依次为顶点 1 1 1至顶点 N N N的权值。
输出格式
输出只有一行,为所有三角形的顶点权值乘积之和的最小值。
数据范围
N \\le 50,
数据保证所有顶点的权值都小于 10 9 10^9 109。
思路
这道题和上一题很相似,在任意一个多边形中选取一条线,再任选一个顶点即可构成一个三角形,整个多边形会被这个三角形划分为三个区域,由于题目中提到分割成的三角形是互不相交的,因此三个区域都是独立的,那么整个状态就被划分为了子状态。
例如,一个凸多边形的顶点按顺序为 ( 1 , 2 , 3 , 4 , 5 , 6 ) (1,2,3,4,5,6) (1,2,3,4,5,6),选取 ( 1 , 4 , 6 ) (1,4,6) (1,4,6)构成一个三角形,那么就会将整个凸多边形划分为三个区域 ( 1 , 2 , 3 , 4 ) , ( 1 , 4 , 6 ) , ( 4 , 5 , 6 ) (1,2,3,4),(1,4,6),(4,5,6) (1,2,3,4),(1,4,6),(4,5,6)。那么对于整个状态的 f [ 1 ] [ 6 ] f[1][6] f[1][6]就会划分为 f [ 1 ] [ 4 ] + f [ 4 ] [ 6 ] + w [ 1 ] ∗ w [ 4 ] ∗ w [ 6 ] f[1][4] + f[4][6] + w[1] * w[4] * w[6] f[1][4]+f[4][6]+w[1]∗w[4]∗w[6]。
推广至一般情况,对于状态表示,使用 f [ l ] [ r ] f[l][r] f[l][r]表示所有将 ( l , l + 1 ) ( l + 1 , l + 2 ) , ⋯ , ( r − 1 , r ) , ( r , l ) (l, l + 1)(l + 1, l + 2),\cdots,(r - 1, r),(r,l) (l,l+1)(l+1,l+2),⋯,(r−1,r),(r,l)划分三角形的方案,属性是最小值。
对于状态划分,可以根据 ( l , r ) (l,r) (l,r)的中间点 k k k进行划分,即将 ( l , k , r ) (l,k,r) (l,k,r)划分为一个三角形,下面就会将 ( l , r ) (l,r) (l,r)的四边形划分为三个子区域,状态转移为 f [ l ] [ k ] + f [ k ] [ r ] + w [ l ] ∗ w [ k ] ∗ w [ r ] f[l][k] + f[k][r] + w[l] * w[k] * w[r] f[l][k]+f[k][r]+w[l]∗w[k]∗w[r]与上一题一样。
需要指出的是,这一题的数据范围非常大, 因此需要高精度,可以先把代码思路写对后,将对应的部分替换为高精度。
代码
cpp
#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 55, M = 35;
int n;
int w[N];
LL f[N][N][M];
void add(LL a[], LL b[])
{
static LL c[M];
memset(c, 0, sizeof c);
for(int i = 0, t = 0; i < M; i ++)
{
t += a[i] + b[i];
c[i] = t % 10;
t /= 10;
}
memcpy(a, c, sizeof c);
}
void mul(LL a[], LL b)
{
static LL c[M];
LL t = 0;
memset(c, 0, sizeof c);
for(int i = 0; i < M; i ++)
{
t += a[i] * b;
c[i] = t % 10;
t /= 10;
}
memcpy(a, c, sizeof c);
}
int cmp(LL a[], LL b[])
{
for(int i = M - 1; i >= 0; i --)
if(a[i] > b[i]) return 1;
else if(a[i] < b[i]) return -1;
return 0;
}
void print(LL a[])
{
int k = M - 1;
while(k && !a[k]) k --;
while(k >= 0) cout << a[k --];
cout << endl;
}
int main()
{
cin >> n;
for(int i = 1; i <= n; i ++) cin >> w[i];
LL temp[M];
for(int len = 3; len <= n; len ++ )
{
for(int l = 1; l + len - 1 <= n; l ++)
{
int r = l + len - 1;
f[l][r][M - 1] = 1;
for(int k = l + 1; k < r; k ++)
{
memset(temp, 0, sizeof temp);
temp[0] = w[l];
mul(temp, w[k]);
mul(temp, w[r]);
add(temp, f[l][k]);
add(temp, f[k][r]);
if(cmp(f[l][r], temp) > 0)
memcpy(f[l][r], temp, sizeof temp);
}
}
}
print(f[1][n]);
return 0;
}Acwing 479. 加分二叉树
设一个 n n n个节点的二叉树的中序遍历为 ( 1 , 2 , 3 , ⋯ , n ) (1,2,3,\cdots,n) (1,2,3,⋯,n),其中数字 1 , 2 , 3 , ⋯ , n 1,2,3,\cdots,n 1,2,3,⋯,n为节点编号。
每个节点都有一个分数(均为正整数),记第 i i i个节点的分数为 d i d_i di,tree 及它的每个子树都有一个加分,任一棵子树 subtree(也包含 tree 本身)的加分计算方法如下:
subtree的左子树的加分 ×× subtree的右子树的加分 ++ subtree的根的分数
若某个子树为空,规定其加分为 1 1 1.
叶子的加分就是叶节点本身的分数,不考虑它的空子树。
试求一棵符合中序遍历为 ( 1 , 2 , 3 , ⋯ , n ) (1,2,3,\cdots,n) (1,2,3,⋯,n)且加分最高的二叉树 tree。
要求输出:
(1)tree的最高加分
(2)tree的前序遍历
输入格式
第一行一个整数 n n n,为节点个数。
第二行 n n n个用空格隔开的整数,为每个节点的分数 ( 0 < 分数 < 100 ) (0 < 分数 < 100) (0<分数<100)。
输出格式
第一行一个整数,为最高加分
第二行 n n n个用空格隔开的整数,为该树的前序遍历。如果存在多种方案,则输出字典序最小的方案。
数据范围
n \\le 30,
思路
同样地,使用 f [ l ] [ r ] f[l][r] f[l][r]表示所有中序遍历是 ( l , r ) (l, r) (l,r)这一段的二叉树集合,属性是最大值。
而对于状态划分,很明显可以根据根节点的不同进行划分。假设根节点在第个 k k k点,那么其左子树就是 ( l , k − 1 ) (l, k - 1) (l,k−1),右子树就是 ( k + 1 , r ) (k + 1, r) (k+1,r),那么整体的最大值就是这三部分的最大值计算得到分别为 f [ l ] [ k − 1 ] f[l][k - 1] f[l][k−1], f [ k + 1 ] [ r ] f[k + 1][r] f[k+1][r], w [ k ] w[k] w[k]。
但是题目还需要记录方案。和前面[背包模型四](数据结构与算法学习笔记(Acwing提高课)----动态规划·背包模型(四)-CSDN博客)中的背包模型求方案数一样,多开一个数组 g [ l ] [ r ] g[l][r] g[l][r],表示是从哪里转移过来的。假设根节点是 R R R,那么 R = g [ 1 ] [ N ] R = g[1][N] R=g[1][N],然后就知道左子树为 ( 1 , R − 1 ) (1,R - 1) (1,R−1),右子树为 ( R + 1 , N ) (R + 1, N) (R+1,N),继续递归即可。
代码
cpp
#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 30;
int n;
int w[N];
int f[N][N], g[N][N];
void dfs(int l, int r)
{
if(l > r) return ;
int root = g[l][r];
cout << root << ' ';
dfs(l, root - 1);
dfs(root + 1, r);
}
int main()
{
cin >> n;
for(int i = 1; i <= n; i ++) cin >> w[i];
for(int len = 1; len <= n; len ++)
for(int l = 1; l + len - 1 <= n; l ++)
{
int r = l + len - 1;
if(len == 1)
{
f[l][r] = w[l];
g[l][r] = l;
}
else
{
for(int k = l; k <= r; k++)
{
int left = k == l ? 1 : f[l][k - 1];
int right = k == r ? 1 : f[k + 1][r];
int score = left * right + w[k];
if(f[l][r] < score)
{
f[l][r] = score;
g[l][r] = k;
}
}
}
}
cout << f[1][n] << endl;
dfs(1,n);
return 0;
}Acwing 321. 棋盘分割
将一个 8 × 8 8 \times 8 8×8的棋盘进行如下分割:将原棋盘割下一块矩形棋盘并使剩下部分也是矩形,再将剩下的部分继续如此分割,这样割了 ( n − 1 ) (n - 1) (n−1)次后,连同最后剩下的矩形棋盘共有 n n n块矩形棋盘。(每次切割都只能沿着棋盘格子的边进行)。
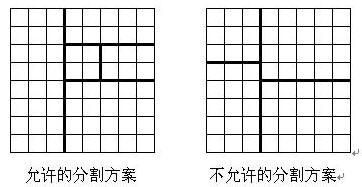
原棋盘上每一格有一个分值,一块矩形棋盘的总分为其所含各格分值之和。
现在需要把棋盘按上述规则分割成 n n n块矩形棋盘,并使各矩形棋盘总分的均方差最小。
均方差 σ = ∑ i = 1 n ( x i − x ˉ ) 2 n \sigma = \sqrt{\frac{\sum_{i = 1}^{n}(x_i - \bar{x})^2}{n}} σ=n∑i=1n(xi−xˉ)2 ,其中平均值为 x ˉ = ∑ i = 1 n x i n \bar{x} = \frac{\sum_{i = 1}^{n}x_i}{n} xˉ=n∑i=1nxi, x i x_i xi为第 i i i块矩形棋盘的总分。
请编程对给出的棋盘及 n n n,求出均方差的最小值。
输入格式
第一行一个整数 n n n。
第二行至第 9 9 9行每行 8 8 8个小于 100 100 100的非负整数,表示棋盘上相应格子的分值。每行相邻两数之间用一个空格分隔。
输出格式
输出最小均方差值(四舍五入精确到小数点后三位)。
数据范围
1 < n < 15 1 < n < 15 1<n<15,
思路
要使均方差最小,可尝试将均方差公式展开进行化简:
∑ i = 1 n ( x i − x ˉ ) 2 n = 1 n ( ∑ i − 1 n ( x i 2 − 2 x i x ˉ + x ˉ 2 ) ) = 1 n ( ∑ i − 1 n x i 2 − x ˉ ∑ i − 1 n 2 x i + n x ˉ 2 ) = 1 n ( ∑ i − 1 n x i 2 − n x ˉ 2 ) = ∑ i − 1 n x i 2 n − x ˉ 2 \begin{align} \frac{\sum_{i = 1}^{n}(x_i - \bar{x})^2}{n} &= \frac{1}{n}(\sum_{i - 1}^n(x_i^2 - 2x_i \bar{x} + \bar{x}^2)) \notag\\ &= \frac{1}{n}(\sum_{i - 1}^nx_i^2 - \bar{x}\sum_{i - 1}^{n}2x_i + n\bar{x}^2) \notag\\ &= \frac{1}{n}(\sum_{i - 1}^nx_i^2 - n\bar{x}^2) \notag\\ &= \frac{\sum_{i - 1}^nx_i^2 }{n} - \bar{x}^2 \end{align} n∑i=1n(xi−xˉ)2=n1(i−1∑n(xi2−2xixˉ+xˉ2))=n1(i−1∑nxi2−xˉi−1∑n2xi+nxˉ2)=n1(i−1∑nxi2−nxˉ2)=n∑i−1nxi2−xˉ2
目标就是最小化上式的结果,由于平均值 x ˉ \bar{x} xˉ是固定的,因此只要最小化前一项即可,也就是每一部分的平方和。
当然,这道题也可以直接进行计算不用化简。直接最小化均方差, x ˉ \bar{x} xˉ是可以直接求出来的,
对于状态表示,这题为 f [ x 1 ] [ y 1 ] [ x 2 ] [ y 2 ] [ k ] f[x1][y1][x2][y2][k] f[x1][y1][x2][y2][k],表示子矩阵 ( x 1 , y 1 , x 2 , y 2 ) (x1,y1,x2,y2) (x1,y1,x2,y2)切分成 k k k部分的所有方案,属性就是均方差的最小值。
对于状态划分,找最后一个不同点,也就是如何切割的。根据横切和纵切分为两大类,在横切中,可以选任意一行进行切割,并且在切割完后将图形分为的上下两部分可以再次划分,任意选取一个图形继续切割,对于纵切也是一样的。那么例如对于横切一次后生成的两部分,如果选择上面的继续切,那就会有上面继续切的分值,和下面剩余已经作为独立一个区域的分值,假设选取了第 i i i行进行横切,那么上面一部分的分值就是 f [ x 1 ] [ y 1 ] [ i ] [ y 2 ] f[x1][y1][i][y2] f[x1][y1][i][y2],求和的话就是二维前缀和。
这题y总讲的是记忆化搜索的做法。
代码
cpp
#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
#include <cmath>
using namespace std;
const int N = 15, M = 9;
const double inf = 1e9;
int n, m = 8;
int s[N][N];
double f[M][M][M][M][N];
double X;
double get(int x1, int y1, int x2, int y2)
{
double sum = s[x2][y2] - s[x2][y1 - 1] - s[x1 - 1][y2] + s[x1 - 1][y1 - 1] - X;
return sum * sum / n;
}
double dp(int x1, int y1, int x2, int y2, int k)
{
double &v = f[x1][y1][x2][y2][k];
if(v >= 0) return v;
if(k == 1) return v = get(x1, y1, x2, y2);
v = inf;
for(int i = x1; i < x2; i ++)
{
v = min(v, dp(x1, y1, i, y2, k - 1) + get(i + 1, y1, x2, y2));
v = min(v, dp(i + 1, y1, x2, y2, k - 1) + get(x1, y1, i, y2));
}
for(int i = y1; i < y2; i ++)
{
v = min(v, dp(x1, y1, x2, i, k - 1) + get(x1, i + 1, x2, y2));
v = min(v, dp(x1, i + 1, x2, y2, k - 1) + get(x1, y1, x2, i));
}
return v;
}
int main()
{
cin >> n;
for(int i = 1; i <= m; i ++)
for(int j = 1; j <= m; j ++)
{
cin >> s[i][j];
s[i][j] += s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1];
}
memset(f, -1, sizeof f); // 这样处理后数组里存的都是NaN,
X = (double)s[m][m] / n; //需要注意这里是整数除法,要转化为double,不然会丢失精度
printf("%.3lf\n", sqrt(dp(1, 1, 8, 8, n)));
return 0;
}