长短期记忆（LSTM）网络模型

一、概述

长短期记忆（Long Short-Term Memory，LSTM）网络是一种特殊的循环神经网络（RNN），专门设计用于解决传统 RNN 在处理长序列数据时面临的梯度消失 / 爆炸问题，能够有效捕捉长距离依赖关系。其核心在于引入记忆细胞（Cell State）和门控机制（Gate Mechanism），通过控制信息的流动来实现对长期信息的存储与遗忘。

二、模型原理

LSTM 由记忆细胞和三个门控单元（遗忘门、输入门、输出门）组成，每个门控单元通过 sigmoid 激活函数输出 0 到 1 之间的数值，表示允许信息通过的程度（0 表示完全禁止，1 表示完全允许）。

1. 记忆细胞状态

记忆细胞状态就像一条信息传输的 "高速公路"，它贯穿整个 LSTM 网络，负责在不同时间步之间传递信息。信息在记忆细胞状态中传递时，可以相对稳定地保留较长时间，避免了传统 RNN 中信息容易丢失的问题。遗忘门和输入门共同作用于记忆细胞状态，遗忘门决定删除哪些旧信息，输入门决定添加哪些新信息 ，从而实现对记忆细胞状态的更新。

2. 输入门

输入门负责处理当前时刻的输入信息，决定哪些新的信息会被添加到记忆细胞状态中。它利用 sigmoid 函数输出一个值，用于控制新信息的 "准入程度"。同时，输入内容通过 tanh 函数生成一个候选值向量，这个向量包含了可能要添加到记忆细胞状态中的新信息。最后，将 sigmoid 函数的输出与 tanh 函数生成的候选值向量相乘，得到实际要添加到记忆细胞状态中的信息。

3. 遗忘门

遗忘门决定了上一时刻记忆细胞状态中哪些信息会被保留到当前时刻。它接收上一时刻的隐藏状态和当前时刻的输入，通过一个 sigmoid 激活函数输出一个 0 到 1 之间的数值。这个数值就像一把 "钥匙"，数值越接近 1，表示上一时刻的该部分信息被保留的程度越高；数值越接近 0，则表示该部分信息被遗忘的程度越高。例如，在处理一段文字序列时，如果之前的内容与当前句子的主题关联不大，遗忘门就会降低这些信息的保留程度。

4. 输出门

输出门根据当前记忆细胞状态和隐藏状态，决定最终的输出。它首先使用 sigmoid 函数得到一个控制输出的向量。然后，对记忆细胞状态进行 tanh 处理，将处理后的记忆细胞状态与 sigmoid 函数的输出向量相乘，从而得到 LSTM 单元的最终输出。

一个典型LSTM的单元结构为

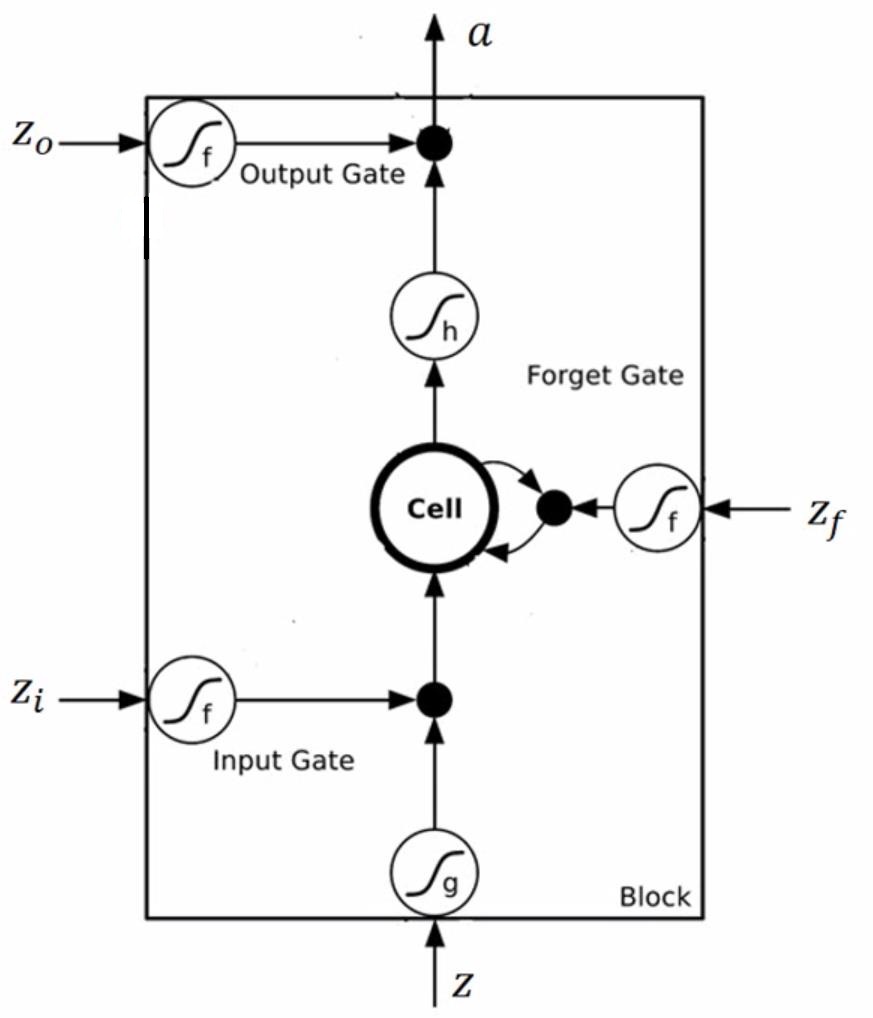
也就是说，对每个LSTM单元，都有四个输入、一个输出，这四个输入也就是对同一组输入数据的线性组合，只是组合了不同参数。具体的计算过程图示为

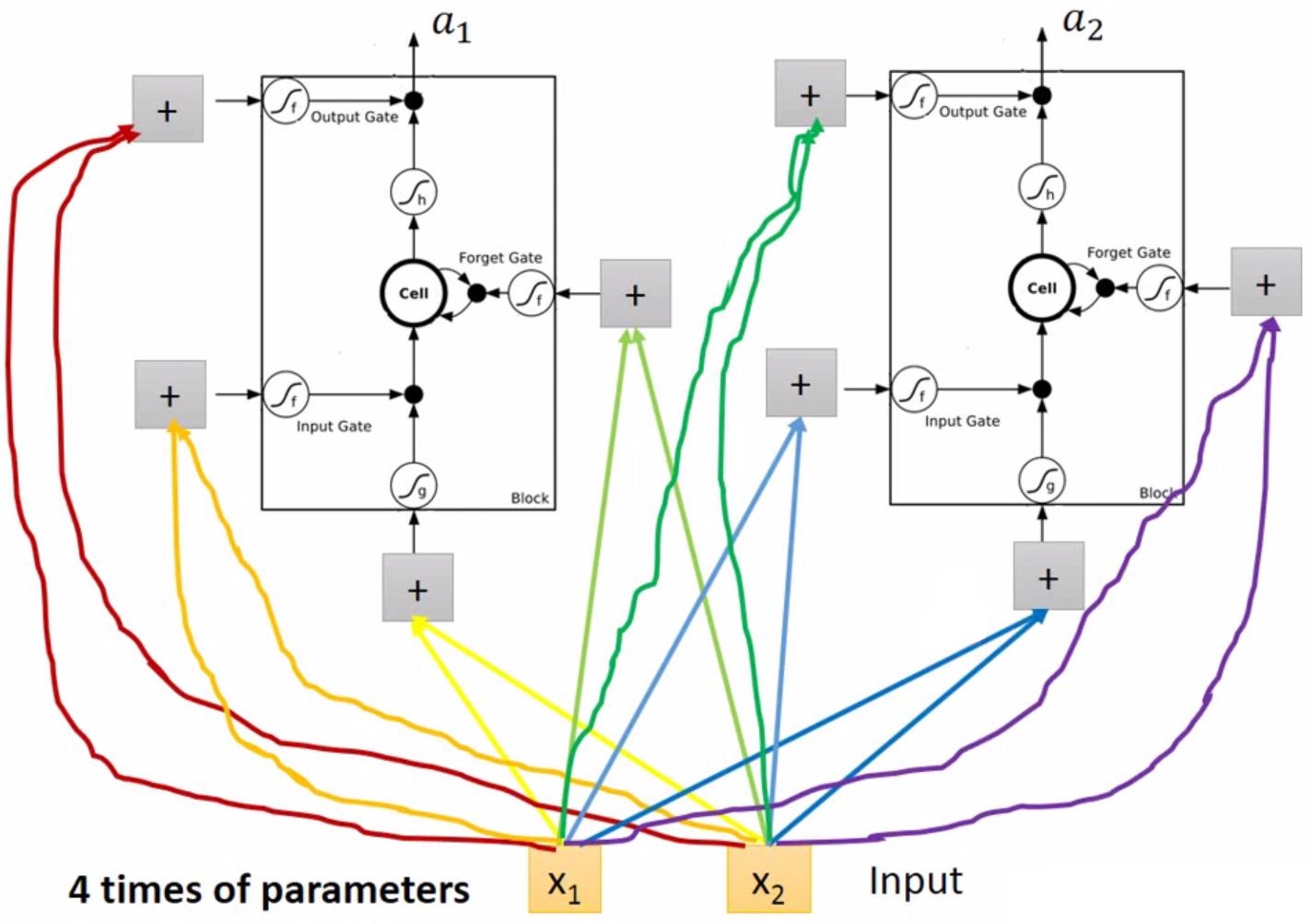
显然，相较于传统的网络结构，LSTM具有四倍的参数量。

三、优势与局限

1. 优势

LSTM 的门控机制使其在处理长序列数据时，能够有效保留和更新信息，避免梯度消失和梯度爆炸问题，从而学习到长距离的依赖关系，在许多序列数据处理任务中取得了优异的成绩。此外，LSTM 的结构具有较好的通用性，可以适应多种不同类型的序列数据处理任务。

2. 局限

由于其结构相对复杂，包含多个门和大量参数，训练过程通常需要更多的计算资源和时间，并且容易出现过拟合问题。同时，LSTM 在解释性方面相对较差，难以直观地理解模型是如何做出决策的。

四、应用领域

1. 自然语言处理

在自然语言处理任务中，LSTM 被广泛应用于文本分类、机器翻译、语音识别、问答系统等。例如，在机器翻译中，LSTM 可以将源语言句子的语义信息编码成固定长度的向量，然后通过解码过程将其转换为目标语言句子；在语音识别中，LSTM 能够处理语音信号中的时间序列信息，将语音转换为文字。

2. 时间序列预测

LSTM 在时间序列预测领域表现出色，如股票价格预测、天气预测、电力负荷预测等。由于 LSTM 能够有效捕捉时间序列中的长期依赖关系，相比传统方法，它可以更准确地预测未来趋势。例如，在股票价格预测中，LSTM 可以分析历史股价数据中的复杂模式，预测未来股价走势。

3. 其他领域

此外，LSTM 还在视频分析、生物信息学等领域得到应用。在视频分析中，LSTM 可以处理视频帧序列，实现动作识别、视频内容理解等任务；在生物信息学中，LSTM 可用于基因序列分析，预测基因功能等。

五、Python实现示例

（环境：Python 3.11，PyTorch 2.4.0）

import matplotlib
matplotlib.use('TkAgg')

import torch
import torch.nn as nn
import numpy as np
import matplotlib.pyplot as plt
from torch.utils.data import DataLoader, TensorDataset

# 设置matplotlib的字体
plt.rcParams['font.sans-serif'] = ['SimHei']  # 'SimHei' 是黑体，也可设置 'Microsoft YaHei' 等
plt.rcParams['axes.unicode_minus'] = False  # 正确显示负号


# 设置随机种子，保证结果可复现
torch.manual_seed(42)
np.random.seed(42)


# 生成示例数据（正弦波序列）
def generate_sequence(length, freq=0.1):
    """生成正弦波序列作为示例数据"""
    x = np.linspace(0, 2 * np.pi * freq, length)
    return np.sin(x)


def create_sequences(data, seq_length):
    """将数据转换为序列和对应目标值的形式"""
    xs, ys = [], []
    for i in range(len(data) - seq_length):
        x = data[i:i + seq_length]
        y = data[i + seq_length]
        xs.append(x)
        ys.append(y)
    return np.array(xs), np.array(ys)


# 生成数据
seq_length = 10
data = generate_sequence(1000)
x, y = create_sequences(data, seq_length)

# 转换为PyTorch张量
x_tensor = torch.FloatTensor(x).view(-1, seq_length, 1)
y_tensor = torch.FloatTensor(y).view(-1, 1)

# 创建数据加载器
dataset = TensorDataset(x_tensor, y_tensor)
train_size = int(0.8 * len(dataset))
train_dataset, test_dataset = torch.utils.data.random_split(dataset, [train_size, len(dataset) - train_size])
train_loader = DataLoader(train_dataset, batch_size=32, shuffle=True)
test_loader = DataLoader(test_dataset, batch_size=32, shuffle=False)


# 定义LSTM模型
class LSTMModel(nn.Module):
    def __init__(self, input_size=1, hidden_size=50, num_layers=1, output_size=1):
        super(LSTMModel, self).__init__()
        self.hidden_size = hidden_size
        self.num_layers = num_layers

        # LSTM层
        self.lstm = nn.LSTM(input_size, hidden_size, num_layers, batch_first=True)

        # 全连接层
        self.fc = nn.Linear(hidden_size, output_size)

    def forward(self, x):
        # 初始化隐藏状态和细胞状态
        h0 = torch.zeros(self.num_layers, x.size(0), self.hidden_size).to(x.device)
        c0 = torch.zeros(self.num_layers, x.size(0), self.hidden_size).to(x.device)

        # 前向传播LSTM
        out, _ = self.lstm(x, (h0, c0))

        # 只取序列中的最后一个时间步的输出
        out = self.fc(out[:, -1, :])
        return out


# 初始化模型、损失函数和优化器
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
model = LSTMModel(input_size=1, hidden_size=50, num_layers=1, output_size=1).to(device)
criterion = nn.MSELoss()
optimizer = torch.optim.Adam(model.parameters(), lr=0.001)


# 训练模型
def train_model(model, train_loader, criterion, optimizer, epochs=100):
    model.train()
    for epoch in range(epochs):
        total_loss = 0
        for inputs, targets in train_loader:
            inputs, targets = inputs.to(device), targets.to(device)

            # 清零梯度
            optimizer.zero_grad()

            # 前向传播
            outputs = model(inputs)
            loss = criterion(outputs, targets)

            # 反向传播和优化
            loss.backward()
            optimizer.step()

            total_loss += loss.item()

        if (epoch + 1) % 10 == 0:
            print(f'Epoch [{epoch + 1}/{epochs}], Loss: {total_loss / len(train_loader):.4f}')


# 评估模型
def evaluate_model(model, test_loader):
    model.eval()
    predictions = []
    actuals = []
    with torch.no_grad():
        for inputs, targets in test_loader:
            inputs, targets = inputs.to(device), targets.to(device)
            outputs = model(inputs)
            predictions.extend(outputs.cpu().numpy())
            actuals.extend(targets.cpu().numpy())
    return np.array(predictions), np.array(actuals)


# 训练模型
train_model(model, train_loader, criterion, optimizer, epochs=50)

# 评估模型
predictions, actuals = evaluate_model(model, test_loader)

# 可视化结果
plt.figure(figsize=(10, 6))
plt.plot(actuals, label='Actual Values')
plt.plot(predictions, label='Predicted Values')
plt.title('LSTM预测结果')
plt.xlabel('样本')
plt.ylabel('值')
plt.legend()
plt.show()

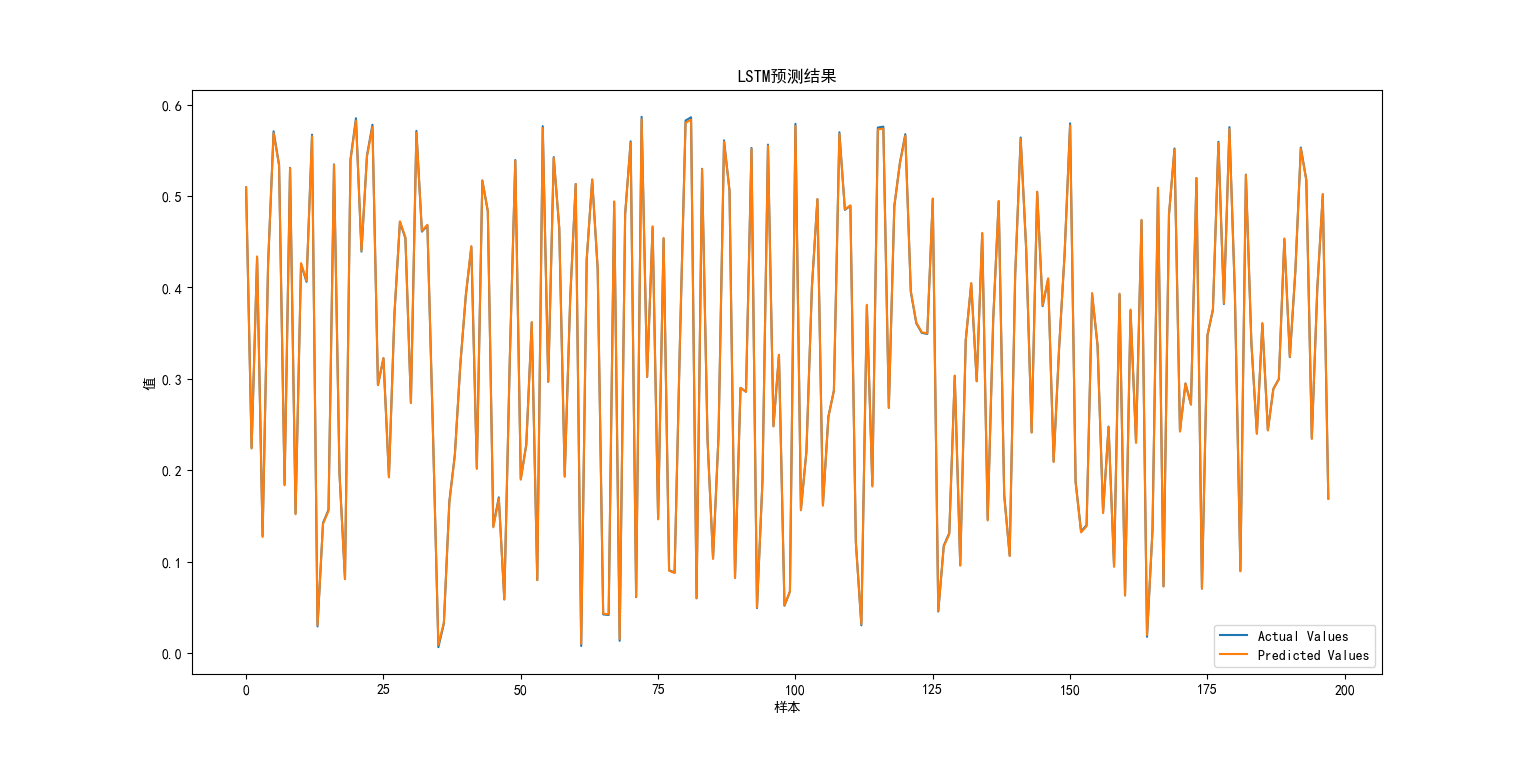
示例实现了一个基本的 LSTM 模型，用于预测正弦波序列的下一个值。主要包括以下几个部分：

数据生成 ：创建一个正弦波序列，并将其转换为适合 LSTM 训练的序列格式。

模型定义 ：定义了一个包含 LSTM 层和全连接层的模型，用于处理序列数据并输出预测结果。

训练过程 ：使用均方误差损失函数和 Adam 优化器训练模型。

评估和可视化：评估模型性能并可视化预测结果与实际值的对比。

可以通过修改参数如seq_length（序列长度）、hidden_size（LSTM 隐藏层大小）、num_layers（LSTM 层数）等来调整模型，也可以将此框架应用于其他序列预测任务。

End.