【算法】动态规划

一、动态规划的基本思想

1. 动态规划算法与分治法类似 ，其基本思想也是将待求解的较大规模问题分解为若干个较小的子问题，先求解子问题，再从这些子问题的解得到原问题的解。

2. 但动态规划法有自己的特点 。分治法的子问题相互独立，适合动态规划算法求解的问题，经分解得到的子问题往往不是互相独立的。

3. 如果子问题不是互相独立的，在用分治法求解时，有些子问题被重复计算许多次 。如果能够保存已解决的子问题的答案，而在需要时再找出已求得的答案，就可以避免大量重复计算。

二、案例

1. 最短路径问题

【问题描述】

输入：起点集合{S1,S2,...,Sn}，

终点集合{T1,T2,...,Tm}，

中间结点集，边集E，

对于任意边有长度输出：一条从起点到终点的最短路

算法设计

蛮力穷举算法：

考察每一条从某个起点到某个终点的路径，计算长度，从中找出最短路径。在示例实例中，如果网络的层数为k，那么路径条数为O(2k)

动态规划算法求解：

动态规划并不能解决所有问题

子问题的界定，后边界不变，前边界前移

优化函数的特点 ：任何最短路的子路径相对于子问题的始点终点最短！
优化原则/最优子结构性质 : 一个最优决策序列的任何子序列本身一定是

相对于子序列的初始和结束状态的最优决策序列。

并非所有问题都满足 优化原则/最优子结构性质，即动态规划并不能解决所有问题。

2. 一个反例

求总长模10的最小路径

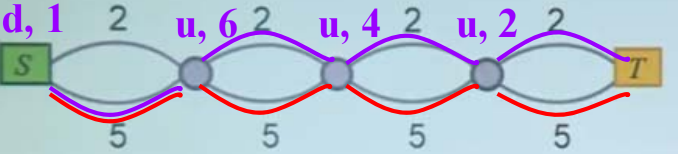
动态规划法得到的解：下、上、上、上

正确的最优解：下、下、下、下

1. 动态规划算法求解过程是多阶段决策过程，每步处理一个子问题，可用于求解组合优化问题。
2. 动态规划算法适用条件：问题要满足优化原则/最优子结构性质，即一个最优决策序列的任何子序列本身一定是相对于子序列的初始和结束状态的最优决策序列。

3. 动态规划要考虑的问题

1. 问题抽象建模：优化的目标函数是什么？约束条件是什么？
2. 如何划分子问题（边界）？
3. 问题的优化函数值与子问题的优化函数值存在着什么依赖关系？（找出递推方程）
4. 是否满足优化原则/最优子结构性质？
5. 最小子问题怎么界定？其优化函数值（初值）是什么？

动态规划算法设计的要素

1. 与蛮力算法相比较，动态规划算法利用了子问题优化函数间的依赖关系，时间复杂度有所降低
2. 动态规划算法的递归实现效率不高 ，原因在于同一子问题多次重复出现，每次出现都需要重新计算一遍
3. 可以采用空间换时间 策略，记录每个子问题首次计算结果，后面再用时就直接取值，每个子问题只算一次

4. 矩阵连乘问题/矩阵链相乘

【问题描述】给定n个矩阵 ， 其中 与 是可乘的， 。 {A1, A2 ,..., An}Ai Ai+1 i=1,2,...,n−1试确定矩阵的乘法顺序，使得元素相乘的总次数最小。

1. 由于矩阵乘法满足结合律，所以计算矩阵的连乘 可以有 A1A2...An许多不同的计算次序。这种计算次序可以用加括号的方式来确定。
2. 若一个矩阵连乘积的计算次序完全确定，也就是说该连乘积已完全加括号，则可以依此次序反复调用2个矩阵相乘的标准算法计算出矩阵连乘积。

输入 ：向量P=<P0,P1,...,Pn>，其中P0,P1,...,Pn为n个矩阵的行数和列数
输出：矩阵链乘法加括号的位置

矩阵Aixj与矩阵Bjxk的乘法，得到C=AB为i行k列的矩阵

矩阵C 的每个元素需要做j次乘法得到，计算AB总计算次数为ijk

输入：向量P =<10,100,5,50 >

即：A1:10x100, A2:100x5, A3:5x50

乘法次序不同运算量不同 ：

(A1A2)A3:10x100x5 + 100x5x50 = 7500 计算次数少 很多！

A1(A2A3):10x100x50 + 100x5x50 = 75000

动态规划算法的基本要素

最优子结构

1. 矩阵连乘计算次序问题的最优解包含着其子问题的最优解。这种性质称为最优子结构性质。
2. 在分析问题的最优子结构性质时，所用的方法具有普遍性：首先假设由问题的最优解导出的子问题的解不是最优的，然后再设法说明在这个假设下可构造出比原问题最优解更好的解，从而导致矛盾。(反证法)
3. 利用问题的最优子结构性质，以自底向上的方式递归地从子问题的最优解逐步构造出整个问题的最优解。最优子结构是问题能用动态规划算法求解的前提。

注意 ：同一个问题可以有多种方式刻划它的最优子结构，有些表示

方法的求解速度更快（空间占用小，问题的维度低）

重叠子问题

1. 递归算法求解问题时，每次产生的子问题并不总是新问题，有些
   子问题被反复计算多次。这种性质称为子问题的重叠性质。
2. 动态规划算法，对每一个子问题只解一次，而后将其解保存在一
   个表格中，当再次需要解此子问题时，只是简单地用常数时间查
   看一下结果。
3. 通常不同的子问题个数随问题的大小呈多项式增长。因此用动态
   规划算法只需要多项式时间，从而获得较高的解题效率。

备忘录方法

备忘录方法的控制结构与直接递归方法的控制结构相同，区别在于备忘录方法为每个解过的子问题建立了备忘录以备需要时查看，避免了相同子问题的重复求解。

5. 凸多边形最优三角剖分

【问题描述】

1. 用多边形顶点的逆时针序列表示凸多边形，即P={v0,v1,...,vn-1}表示具有n条边的凸多边形。

2. 若vi与vj是多边形上不相邻的2个顶点，则线段vivj称为多边形的一条弦。弦将多边形分割成2个多边形{vi,vi+1,...,vj}和{vj,vj+1,...vi}。

3. 多边形的三角剖分是将多边形分割成互不相交的三角形的弦的集合T。

4. 给定凸多边形P，以及定义在由多边形的边和弦组成的三角形上的权函数w。要求确定该凸多边形的三角剖分，使得即该三角剖分中诸三角形上权之和为最小。
   

5. 一个表达式的完全加括号方式相应于一棵完全二叉树，称为表达式的语法树。例如，完全加括号的矩阵连乘积((A1(A2A3))(A4(A5A6)))所相应的语法树如图 (a)所示。

6. 凸多边形{v0,v1,...vn-1}的三角剖分也可以用语法树表示。例如，图 (b)中凸多边形的三角剖分可用图 (a)所示的语法树表示。

7. 矩阵连乘积中的每个矩阵Ai对应于凸(n+1)边形中的一条边vi-1vi。三角剖分中的一条弦vivj，i<j，对应于矩阵连乘积Ai+1:j
   
   最优子结构性质

8. 凸多边形的最优三角剖分问题有最优子结构性质。

9. （反证法）若凸(n+1)边形P={v0,v1,...,vn-1}的最优三角剖分T包含三角形v0 v k vn，1≤k≤n-1，则T的权为3个部分权的和：三角形v0 vk vn的权，子多边形{

   v0,v1,...,vk}和{vk,vk+1,...,vn}的权之和。

   可以断言，由T所确定的这2个子多边形的三角剖分也是最优的。因为若有{v0,v1,...,vk}或{vk,vk+1,...,vn}的更小权的三角剖分将导致T不是最优三角剖分的矛盾。

6. 0-1背包问题

【问题描述】

1. 给定n种物品和一背包。物品i的重量是wi，其价值为vi，背包的容量为C。
2. 问题：应如何选择装入背包的物品，使得装入背包中物品的总价值最大
3. 物品i给要么装入背包，要么不装入背包。不能部分装入、不能装入多次。因此，该问题被称为0-1背包问题。其是一个特殊的整数规划问题。