在数学可视化中,显函数 y=f(x) \\(相对容易处理,但\*\*隐函数\*\*\\) F(x,y)=0 的绘制则更具挑战性。
Manim库中的ImplicitFunction类专门用于解决这个问题,它能够高效地绘制各种复杂的隐函数曲线。
ImplicitFunction的典型应用场景包括:
- 高等数学教学:绘制圆锥曲线(椭圆、双曲线)、心形线、双纽线等
- 工程应用:可视化等值线、等高线、势能面
- 物理模拟:绘制电场/磁场的等势线、相平面轨迹
- 计算机图形学:生成特殊曲线和曲面
- 代数几何:研究代数曲线的性质
今天,我们将深入探讨Manim中的ImplicitFunction类,了解其作用、应用场景以及如何通过实际示例展示其强大功能。
1. 主要参数
ImplicitFunction的主要参数有:
| 参数 | 类型 | 说明 |
|---|---|---|
func |
Callable[[float, float], float] | 必需参数,二元函数F(x,y) |
x_range |
Sequence[float] | x轴的取值范围,如[-3,3] |
y_range |
Sequence[float] | y轴的取值范围,如[-3,3] |
color |
Color | 曲线颜色,默认为WHITE |
min_distance |
float | 点之间的最小距离(控制曲线精度) |
max_quads |
int | 用于渲染的最大四边形数量(性能优化) |
use_smoothing |
bool | 是否使用平滑处理(默认True) |
delta |
float | 采样步长(影响曲线精度) |
func参数是隐式函数的形式,这个函数需要接受两个浮点数 x \\(和\\) y ,并返回一个浮点数。
2. 主要方法
ImplicitFunction的主要方法有:
| 名称 | 说明 |
|---|---|
| generate_points | 初始化points属性,从而定义形状。这个方法在对象创建时被调用 |
| init_points | 与generate_points类似,用于初始化points属性 |
3. 使用示例
为了更好地理解ImplicitFunction的功能,我们将通过几个示例来展示其在不同场景中的应用。
3.1. 基本隐函数(圆)
这个示例展示最基本的隐函数绘制,通过方程 x\^2+ y\^2 = 1 绘制单位圆。
注意 x_range和y_range的设置需要包含整个曲线。
python
# 创建隐函数图像(单位圆)
circle = ImplicitFunction(
lambda x, y: x**2 + y**2 - 1,
color=RED,
x_range=[-1.5, 1.5],
y_range=[-1.5, 1.5],
)
# 添加标签
label = MathTex("x^2 + y^2 = 1").next_to(circle, DOWN)
# 动画展示
self.play(Create(circle), Write(label))
3.2. 动态参数变化(椭圆)
这个示例使用ValueTracker和always_redraw实现动态变化的椭圆,展示如何通过改变参数实时更新隐函数图像。
python
# 创建参数跟踪器
a = ValueTracker(1)
b = ValueTracker(1)
# 创建动态椭圆
ellipse = always_redraw(
lambda: ImplicitFunction(
lambda x, y: (x**2) / (a.get_value() ** 2)
+ (y**2) / (b.get_value() ** 2)
- 1,
color=GREEN,
x_range=[-4, 4],
y_range=[-3, 3],
)
)
# 添加参数标签
param_label = always_redraw(
lambda: MathTex(
f"\\frac{{x^2}}{{{a.get_value()**2:.1f}}} + \\frac{{y^2}}{{{b.get_value()**2:.1f}}} = 1",
color=RED,
)
.shift(DOWN * 1.5 + RIGHT * 1.8)
.scale(0.6)
)
self.add(ellipse, param_label)
self.play(a.animate.set_value(2), b.animate.set_value(1.5), run_time=3)
self.play(a.animate.set_value(3), b.animate.set_value(1), run_time=3)
3.3. 复杂曲线(笛卡尔心形线)
这个示例展示复杂隐函数的绘制,绘制了一个心形曲线。
python
# 创建心形线
heart = ImplicitFunction(
lambda x, y: (x**2 + y**2 - 1) ** 3 - x**2 * y**3,
color=PINK,
x_range=[-1.5, 1.5],
y_range=[-1.2, 1.8],
)
# 添加标签
label = (
MathTex("(x^2 + y^2 - 1)^3 = x^2 y^3", color=GREEN)
.shift(DOWN + RIGHT * 1.8)
.scale(0.6)
)
self.play(Create(heart), Write(label))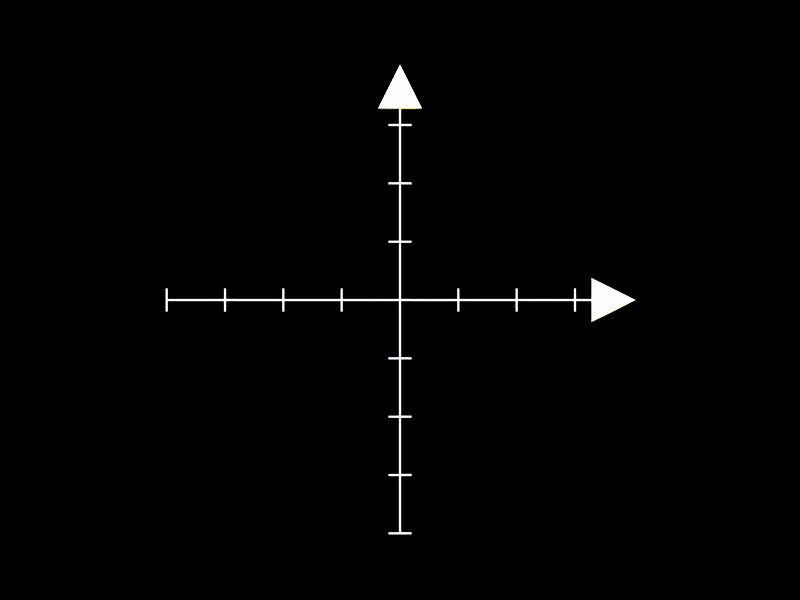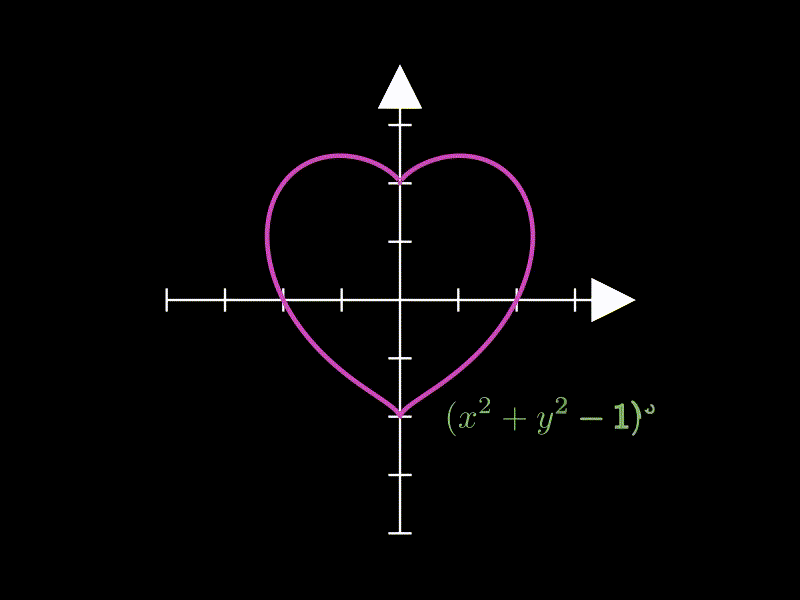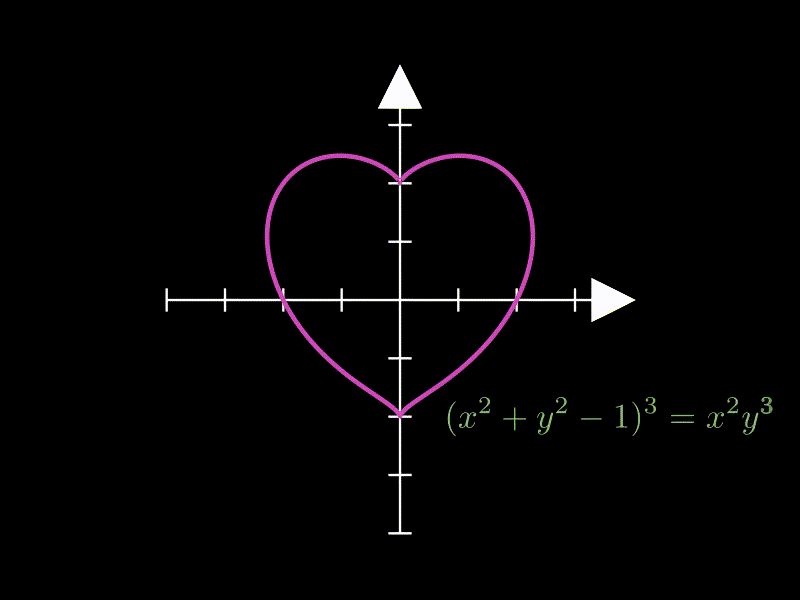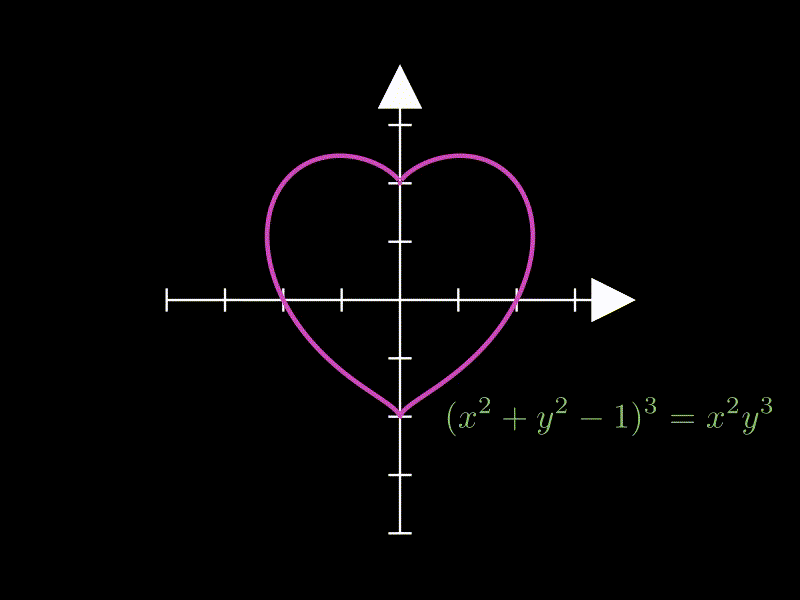
4. 附件
文中的代码只是关键部分的截取,完整的代码共享在网盘中(implicit_function.py),
下载地址: 完整代码 (访问密码: 6872)