拒绝“凭感觉”：用回归分析看透数据背后的秘密

在数据分析的江湖里，有一个绝对的核心技能，叫做回归分析（Regression Analysis）。

无论你是刚入行的新手，还是想要进阶的老手，掌握它，你就拥有了预测未来的"水晶球"。

很多初学者一听到"回归"两个字，脑子里全是复杂的数学公式，立刻想打退堂鼓。

别急！今天我们不讲枯燥的数学推导，只讲它是什么、怎么用，以及如何用Python代码解决实际问题。

1. 什么是回归分析？

想象一下，你正在做饭。你知道火开得越大（变量X），锅里的水烧开的时间就越短（变量Y）。这种探寻变量之间因果关系或相关关系的过程，就是回归分析。

在数据分析中，回归分析主要帮我们解决两个问题：

1. 归因：是谁影响了结果？（比如：是学历还是工作经验决定了你的薪资？）
2. 预测：根据现有数据推测未来。（比如：根据上个月的广告费，预测下个月的销量。）

2. 线性回归：一切的起点

线性回归是最简单、最基础的模型，它假设变量之间的关系是一条直线。

2.1. 简单线性回归

公式： y = ax + b

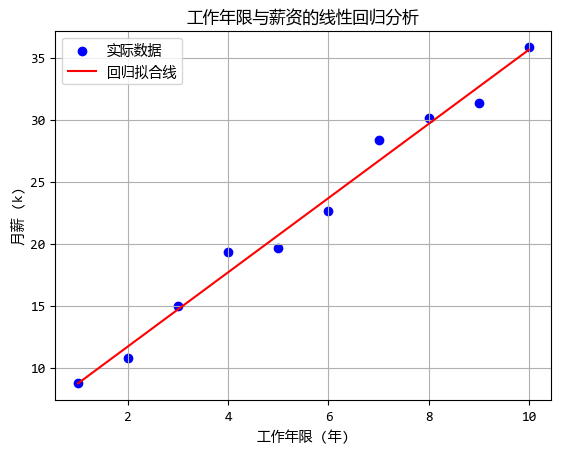
比如我们要研究 **"工作经验"和"薪资"**的关系。

• x ：工作年限
• y ：月薪

这里的核心是找到那个最好的 a （斜率，代表经验每增加一年，工资涨多少）和 b （截距，代表刚毕业时的起薪）。

我们通常使用最小二乘法，简单来说，就是画一条线，让所有实际的数据点到这条线的距离之和最小。

代码示例：预测你的薪资

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression

# 1. 模拟数据：工作年限 vs 月薪 (单位：千元)
# 真实世界中数据总会有波动（加上一些随机噪声）
np.random.seed(42)
X = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10]).reshape(-1, 1) # 工作年限
y = 3 * X + 5 + np.random.normal(0, 1.5, size=(10, 1))      # 假设大概规律是：起薪5k，每年涨3k

# 2. 建立模型并训练
model = LinearRegression()
model.fit(X, y)

# 3. 打印回归系数
print(f"回归方程: y = {model.coef_[0][0]:.2f} * x + {model.intercept_[0]:.2f}")
print("解读：起薪约 {:.2f}k，每年约涨 {:.2f}k".format(model.intercept_[0], model.coef_[0][0]))

# 运行结果：
'''
回归方程: y = 2.99 * x + 5.73
解读：起薪约 5.73k，每年约涨 2.99k
'''

2.2. 多元线性回归

现实生活中，影响薪资的不止是年限，还有学历 、所在城市等。

当自变量 x 变成多个（ x_1, x_2, ... ）时，这就是多元线性回归。

虽然超过3维 画图比较困难，但Python处理起来代码几乎和简单线性回归一样，只是把 X 数据集多加几列而已。

3. 非线性回归：现实世界通常是弯曲的

并不是所有关系都是直线的。比如：

• 细菌分裂：一开始很少，突然爆发（指数函数）。
• 学习曲线：刚开始进步快，后面越来越慢（对数函数）。
• 网红产品生命周期：爆发增长 -> 趋于饱和（S曲线/逻辑函数）。

针对这些非线性关系，我们需要用到不同的"数学模型"来拟合。

以下是 **10种常用非线性模型 **的公式。

我们将使用 Python 的 scipy.optimize.curve_fit 库，这个库非常强大，只要你给出公式，它就能帮你找到参数。

import numpy as np

# --- 定义各种非线性函数 ---

# 1. 二次式 (抛物线，如投篮轨迹)
def func_quadratic(x, a, b, c):
    return a * x**2 + b * x + c

# 2. 三次式 (波动更复杂的数据)
def func_cubic(x, a, b, c, d):
    return a * x**3 + b * x**2 + c * x + d

# 3. 增长函数 (常用于人口增长、复利计算)
def func_growth(x, a, b):
    return np.exp(a * x + b)

# 4. 幂函数 (如物理学中的万有引力、规模效应)
def func_power(x, a, b):
    return a * (x ** b)

# 5. 指数函数 (病毒传播初期)
def func_exponential(x, a, b):
    return a * np.exp(b * x)

# 6. 对数函数 (边际效应递减，如广告投入与销量的后期关系)
def func_logarithmic(x, a, b):
    # 防止x为0报错，通常处理为 x+1 或确保数据 > 0
    return a * np.log(x) + b

# 7. 复合函数 (根据具体复合形式定义，此处示例 y = a * b^x)
def func_compound(x, a, b):
    return a * (b ** x)

# 8. S曲线 (S-Curve, 早期慢，中期快，晚期平缓)
def func_scurve(x, a, b):
    return np.exp(a + b / x)

# 9. 逆函数 (双曲线，如某种反比关系)
def func_inverse(x, a, b):
    return a + b / x

# 10. 逻辑函数 (Logistic, 典型的S型增长，有上限，如市场渗透率)
# u: 上限, a, b: 形状参数
def func_logistic(x, u, a, b):
    return 1 / (1/u + a * (b ** x))

模型类型	数学形式	实际案例	关键特征
二次式模型	y=ax\^2+bx+c	1. 广告投入与销售额（边际递减） 2. 生产成本与产量（U型成本曲线） 3. 车速与燃油效率	• 只有一个极值点 • 描述先增后减或先减后增 • 适合局部非线性
三次式模型	y=ax^3+bx^2+cx+d	1. 经济周期波动分析 2. 复杂化学反应速率 3. 生物生长多阶段模型	• 可有多个极值点 • 描述S型或N型曲线 • 灵活但易过拟合
增长函数	y=e\^{(ax+b)}	1. 病毒传播初期 2. 初创公司用户增长 3. 复利计算	• J型增长曲线 • 增长率恒定 • 无上限增长
幂函数	y=ax\^b	1. 代谢率与体重（克莱伯定律） 2. 城市规模与经济产出 3. 学习曲线（熟练度提升）	• 双对数坐标下呈直线 • 描述规模效应 • b>1：超线性；b<1：次线性
指数函数	y=ae\^{bx}	1. 放射性物质衰变 2. 设备折旧计算 3. 温度冷却过程	• 半对数坐标下呈直线 • b>0：指数增长 • b<0：指数衰减
对数函数	y=a\\ln x+b	1. 技能提升曲线 2. 营销效果递减 3. 收入与幸福感关系	• 初期增长迅速 • 后期趋于平缓 • 描述边际递减效应
复合函数	y=a\^xb	1. 技术创新扩散 2. 社交媒体信息传播 3. 某些生物种群增长	• 变量在指数位置 • 增长速率不断变化 • 形式较为特殊
S曲线	y=e\^{(a+\\frac{b}{x})}	1. 产品生命周期 2. 技术采纳曲线 3. 市场渗透过程	• 描述完整生长周期 • 有拐点 • 最终趋于稳定
逆函数	y=a+\\frac{b}{x}	1. 引力与距离关系 2. 工作效率与干扰频率 3. 服务响应时间与并发数	• 反比例关系 • 快速衰减后趋稳 • 适合渐近线模型
逻辑函数	y=\\frac{1}{\\frac{1}{u}+ab\^x}	1. 人口增长（环境承载力） 2. 市场饱和分析 3. 疾病传播（考虑免疫）	• 完整的S型曲线 • 有明确上限u • 描述有限资源下的增长

4. 实战演练：谁能预测"爆款视频"的流量？

最后，我们来看一个热点案例。

假设你是一个短视频运营，你拿到了一款爆款视频发布后24小时内的累计播放量数据。

你需要判断它的流量走势，以便决定是否追加推广预算。

视频流量通常符合S型增长（逻辑函数）：

1. 冷启动：没人看。
2. 爆发期：被算法推荐，指数级增长。
3. 饱和期：该看的人都看过了，增长停滞。

如果不做分析，直接用线性回归（直线）去预测，后果可能是灾难性的（会预测出无限增长）。

下面的代码尝试了线性回归 和两种不同的非线性回归函数来分析。

# --- 模拟爆款视频数据 ---
x_data = np.linspace(1, 24, 24) # 24小时
# 真实数据模拟：符合逻辑函数分布，上限是100万播放量
y_data = 100 / (1 + 100 * np.exp(-0.5 * (x_data - 10))) + np.random.normal(0, 2, 24)
# y_data 单位是 万次播放

plt.figure(figsize=(12, 8))
plt.scatter(x_data, y_data, label='实际播放量', color='black', marker='o')

# --- 挑战1：尝试用线性回归拟合 (错误的尝试) ---
popt_lin, _ = curve_fit(lambda x, a, b: a*x+b, x_data, y_data)
y_lin = popt_lin[0] * x_data + popt_lin[1]
plt.plot(x_data, y_lin, 'g--', label='线性回归 (太简单了)')

# --- 挑战2：尝试用指数函数拟合 (爆发期还可以，但无法预测饱和) ---
# 指数函数容易溢出，选取部分数据或小心参数初始值，这里仅作演示
try:
    popt_exp, _ = curve_fit(func_exponential, x_data, y_data, maxfev=5000)
    y_exp = func_exponential(x_data, *popt_exp)
    plt.plot(x_data, y_exp, 'y--', label='指数函数 (以为会一直涨)')
except:
    print("指数拟合失败，数据不符合指数特征")

# --- 挑战3：使用逻辑函数 (Logistic) 拟合 (最佳选择) ---
# 逻辑函数公式较复杂，给一些初始猜测值(p0)会有帮助：上限u=100, a=100, b=0.5
# 注意：上面的func_logistic形式需要调整以匹配scipy拟合的稳定性，
# 这里我们使用一个更通用的Logistic形式用于演示：L / (1 + exp(-k(x-x0)))
def standard_logistic(x, L, k, x0):
    return L / (1 + np.exp(-k * (x - x0)))

popt_log, _ = curve_fit(standard_logistic, x_data, y_data, p0=[100, 0.5, 10])
y_log = standard_logistic(x_data, *popt_log)

plt.plot(x_data, y_log, 'r-', linewidth=3, label='逻辑函数 (完美拟合S型)')

# --- 绘图美化 ---
plt.title('爆款视频24小时播放量走势预测', fontsize=16)
plt.xlabel('发布时间 (小时)')
plt.ylabel('累计播放量 (万)')
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()

print(f"预测结论：该视频的流量天花板大约在 {popt_log[0]:.1f} 万次左右。")

# 运行结果：
'''
预测结论：该视频的流量天花板大约在 97.7 万次左右。
'''

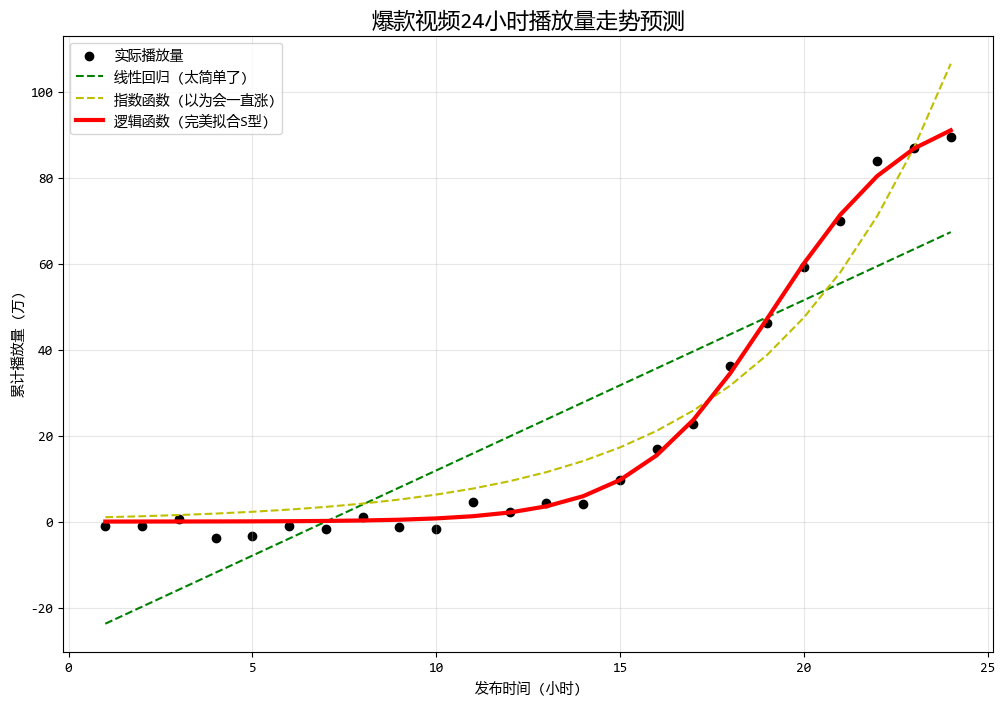
从图中可以看出：

• 绿线（线性）：完全无法捕捉爆发的趋势，早期预测偏高，中期预测偏低，晚期预测又偏低。
• 黄线（指数）：在视频爆发初期（前10小时）拟合得很好，但它会预测24小时后播放量破亿，这显然不符合实际（因为受众是有限的）。
• 红线（逻辑函数）：完美地贴合了数据，不仅抓住了爆发期，还成功预测了流量的"天花板"（饱和点）。

5. 总结：如何选择回归模型？

回归分析 不仅是数据分析师工具箱中的基础工具，更是连接数据 与业务的桥梁。

作为一名数据分析师，选择哪种回归模型，最终还是要根据数据和业务的情况来决定。

1. 先看图 ：拿到数据，先用 plt.scatter() 画散点图。
   • 看着像直线？ -> 线性回归。
   • 看着像抛物线？ -> 二次函数。
   • 看着像先慢后快？ -> 指数函数。
   • 看着像S型？ -> 逻辑函数。
2. 看业务 ：
   • 只要是涉及"资源有限"、"市场饱和"的，多半是 S曲线 或 对数函数。
   • 只要是涉及"病毒传播"、"裂变"的，初期多半是 指数函数。
3. 看误差 ：
   • 用 R\^2 或 均方误差（MSE）来评估，哪个模型误差小，就选哪个。

回归分析 并不难，难的是理解业务背后的逻辑，并选择正确的数学模型去描述它。