因果人工智能——概率生成建模入门

数据智能老司机2025-06-03 13:43

本章内容包括：

  • 概率模型入门
  • 使用 pgmpy 和 Pyro 库进行计算概率
  • 因果关系统计学：数据、总体与模型
  • 区分概率模型与主观贝叶斯主义

第一章论证了学习因果 AI 编程的重要性。本章将介绍我们进行概率机器学习因果建模所需的基础知识。概率机器学习大致指的是利用概率来建模不确定性和模拟数据的机器学习技术。当前有一套灵活且前沿的工具可用于构建概率机器学习模型。本章将介绍概率、统计学、建模、推断乃至哲学等相关概念，这些是实现概率机器学习路径下因果推断关键思想所必需的。

本章不会对这些思想做数学上的全面介绍，而是聚焦于本书后续内容所需，省略其他部分。任何追求因果推断专业能力的数据科学家都不应忽视概率、统计学、机器学习与计算机科学的实践细节。推荐资源请参考章节注释：www.altdeep.ai/p/causalaib... ，可供深入学习和复习。

本章将介绍两个用于概率机器学习的 Python 库：

  • pgmpy：用于构建概率图模型的库。作为传统图模型工具，它的灵活性和前沿程度不及 Pyro，但更易用且便于调试。它擅长完成其设计范围内的功能。
  • Pyro：通用概率机器学习库，基于 PyTorch，灵活且利用了前沿的基于梯度的学习技术。

Pyro 和 pgmpy 是本书主要使用的通用建模库。其他库则专门针对因果推断设计。

2.1 概率入门

我们先复习一下本书所需的概率理论，从几个基本的数学公理和其逻辑推导开始，暂时不加入现实世界的解释。先从一个具体例子说起------一个简单的三面骰子（这类骰子确实存在）。

2.1.1 随机变量与概率

随机变量是指其可能取值是随机现象的数值结果的变量。这些取值可以是离散的，也可以是连续的。本节我们将重点讨论离散随机变量。例如，表示三面骰子掷出的离散随机变量的取值可能是 {1, 2, 3}。在像 Python 这样从 0 开始计数的编程语言中，可能更适合使用 {0, 1, 2}。类似地，表示抛硬币的离散随机变量可能的结果是 {0, 1} 或 {True, False}。图 2.1 展示了三面骰子的示意图。

通常的记法是用大写字母如 X、Y 和 Z 来表示随机变量。例如，假设 X 代表一次掷骰子的结果，其可能取值为 {1, 2, 3}，结果表示骰子朝上的点数。事件 X = 1 和 X = 2 分别表示掷出点数为 1 和 2 的情况。如果我们想用一个变量来抽象具体的结果，通常用小写字母表示。例如，我会用 "X = x"（比如 X = 1）来表示事件"我掷出了 'x'！"其中 x 可以是 {1, 2, 3} 中的任意一个值。见图 2.2。

随机变量的每个取值都有一个概率值。对于离散变量，这个概率值通常称为概率质量（probability mass）；对于连续变量，则称为概率密度（probability density）。离散变量的概率值介于 0 和 1 之间，所有可能取值的概率值加起来等于 1。连续变量的概率密度大于 0，对所有可能结果的概率密度积分之和为 1。

假设一个随机变量取值为 {0, 1}，代表抛硬币的结果，那么 0（反面）对应的概率是多少？1（正面）对应的概率是多少？目前我们只知道这两个概率值都在 0 到 1 之间，且两者相加为 1。要进一步理解，我们需要讨论概率的解释。首先，我们先理清几个相关概念。

2.1.2 概率分布和分布函数

概率分布函数（probability distribution function）是一个函数，将随机变量的取值映射到对应的概率值。例如，如果抛硬币结果为 1（正面），且概率值为 0.51，那么分布函数就把 1 映射为 0.51。我采用标准记法 P(X=x)，比如 P(X=1) = 0.51。对于较长的表达式，当随机变量明确时，我会省略大写字母，只保留取值，即 P(X=x) 写作 P(x)，P(X=1) 写作 P(1)。

如果随机变量只有有限个离散的取值集合，我们可以用表格来表示概率分布。例如，一个随机变量取值为 {1, 2, 3} 的概率分布可以如图 2.3 所示。

在本书中，我采用常用的符号 P(X) 表示随机变量 X 的所有可能结果的概率分布，而 P(X = x) 表示某个具体结果 x 的概率值。为了在 pgmpy 中实现概率分布对象，我们将使用 DiscreteFactor 类。

ini 复制代码 
from pgmpy.factors.discrete import DiscreteFactor
dist = DiscreteFactor(
    variables=["X"],    #1
    cardinality=[3],    #2
    values=[.45, .30, .25],  #3
    state_names= {'X': ['1', '2', '3']}     #4
)
print(dist)
  • #1 因子中变量名称的列表
  • #2 每个变量的基数（可能结果的数量）
  • #3 因子中变量对应的概率值
  • #4 字典，键是变量名称，值是该变量取值名称的列表

该代码输出如下：

scss 复制代码 
+------+----------+
| X    |   phi(X) |
+======+==========+
| X(1) |   0.4500 |
+------+----------+
| X(2) |   0.3000 |
+------+----------+
| X(3) |   0.2500 |
+------+----------+

设置环境

本代码基于 pgmpy 版本 0.1.24 和 Pyro 版本 1.8.6 编写，使用的 pandas 版本为 1.5.3。

更多章节 Jupyter 笔记本、代码和环境配置说明，请参见 www.altdeep.ai/p/causalaib... 。

2.1.3 联合概率与条件概率

在实际推理中，我们通常关注多个随机变量的情况。假设除了图 2.1 中的随机变量 X 之外，还有一个随机变量 Y，取值为 {0, 1}。此时，会存在一个联合概率分布函数，将 X 和 Y 的每一种组合映射到一个概率值。

作为表格，它可以看起来像图 2.4。

DiscreteFactor 对象也可以表示联合分布。

ini 复制代码 
joint = DiscreteFactor(
    variables=['X', 'Y'],   #1
    cardinality=[3, 2],     #2
    values=[.25, .20, .20, .10, .15, .10],     #3
    state_names= {
        'X': ['1', '2', '3'],    #3
        'Y': ['0', '1']          #3
    }
)
print(joint)     #4
  • #1 现在有两个变量，而非一个
  • #2 X 有 3 个可能结果，Y 有 2 个可能结果
  • #3 两个变量均给出了对应的结果名称
  • #4 可以查看打印输出以了解值的排序方式

上述代码打印的输出如下：

scss 复制代码 
+------+------+------------+
| X    | Y    |   phi(X,Y) |
+======+======+============+
| X(1) | Y(0) |     0.2500 |
+------+------+------------+
| X(1) | Y(1) |     0.2000 |
+------+------+------------+
| X(2) | Y(0) |     0.2000 |
+------+------+------------+
| X(2) | Y(1) |     0.1000 |
+------+------+------------+
| X(3) | Y(0) |     0.1500 |
+------+------+------------+
| X(3) | Y(1) |     0.1000 |
+------+------+------------+

注意概率值加和为 1。进一步地，当我们对 Y 沿行进行边缘化（即对 Y 进行"求和"或"积分"），可以恢复原始的分布 P(X)（即 X 的边缘分布）。图 2.5 底部显示了对行求和后得到的 X 的边缘分布。

marginalize 方法会帮我们对指定的变量求和。

示例代码：

ini 复制代码 
print(joint.marginalize(variables=['Y'], inplace=False))

输出结果如下：

scss 复制代码 
+------+----------+
| X    |   phi(X) |
+======+==========+
| X(1) |   0.4500 |
+------+----------+
| X(2) |   0.3000 |
+------+----------+
| X(3) |   0.2500 |
+------+----------+

将 inplace 参数设为 False 会返回一个新的边缘化后的表，而不会修改原始的联合分布表。

同样地，当我们对列上的变量 X 做边缘化时，就得到了 P(Y)。在图 2.6 中，对列上 X 的值求和，就得到了右侧的 Y 的边缘分布。

示例代码：

ini 复制代码 
python
复制
print(joint.marginalize(variables=['X'], inplace=False))

输出结果如下：

scss 复制代码 
diff
复制
+------+----------+
| Y    |   phi(Y) |
+======+==========+
| Y(0) |   0.6000 |
+------+----------+
| Y(1) |   0.4000 |
+------+----------+

我使用符号 P(X, Y) 表示联合分布。用 P(X = x, Y = y) 表示某一具体结果的概率，简写为 P(x, y)。例如，在图 2.6 中，P(X = 1, Y = 0) = P(1, 0) = 0.25。我们可以定义任意数量变量的联合分布；如果有三个变量 {X, Y, Z}，联合分布表示为 P(X, Y, Z)。

在联合概率分布的表格表示中，随着变量数量的增加，单元格数量呈指数增长。虽然存在一些（但不多）"典型"的联合概率分布（比如多元正态分布------我将在第 2.1.7 节中展示更多例子），但在多变量情形中，我们更倾向于使用条件概率分布。

条件概率是指给定 X 的情况下 Y 的概率，公式为 ------

直观来说，P(Y | X = 1) 表示在 X 取值为 1 的条件下，Y 的概率分布。在表格形式的概率分布中，我们可以通过将联合概率分布表中的各个单元格除以对应的边缘概率值，来得到条件概率分布表，如图 2.7 所示。请注意，图 2.7 中条件概率表的每一列现在的和都为 1。

pgmpy 库允许我们使用"/"操作符进行条件概率的计算：

scss 复制代码 
print(joint / dist)

该代码会输出如下结果：

scss 复制代码 
+------+------+------------+
| X    | Y    |   phi(X,Y) |
+======+======+============+
| X(1) | Y(0) |     0.5556 |
+------+------+------------+
| X(1) | Y(1) |     0.4444 |
+------+------+------------+
| X(2) | Y(0) |     0.6667 |
+------+------+------------+
| X(2) | Y(1) |     0.3333 |
+------+------+------------+
| X(3) | Y(0) |     0.6000 |
+------+------+------------+
| X(3) | Y(1) |     0.4000 |
+------+------+------------+

你也可以直接用 TabularCPD 类指定条件概率分布表：

ini 复制代码 
from pgmpy.factors.discrete.CPD import TabularCPD

PYgivenX = TabularCPD(
    variable='Y',               #1
    variable_card=2,            #2
    values=[
        [.25/.45, .20/.30, .15/.25],    #3
        [.20/.45, .10/.30, .10/.25],    #3
    ],
    evidence=['X'],
    evidence_card=[3],
    state_names={
        'X': ['1', '2', '3'],
        'Y': ['0', '1']
    }
)

print(PYgivenX)

输出如下：

scss 复制代码 
+------+--------------------+---------------------+------+
| X    | X(1)               | X(2)                | X(3) |
+------+--------------------+---------------------+------+
| Y(0) | 0.5555555555555556 | 0.6666666666666667  | 0.6  |
+------+--------------------+---------------------+------+
| Y(1) | 0.4444444444444445 | 0.33333333333333337 | 0.4  |
+------+--------------------+---------------------+------+
  • variable_card 参数表示 Y 的基数（即 Y 可能的取值数量）。
  • evidence_card 是 X 的基数。

条件化作为一种操作

在"条件概率"一词中，"条件"是形容词。把"条件"当作动词（操作）来理解会更有帮助。你可以把随机变量 Y 以随机变量 X 为条件来进行"条件化"。例如，在图 2.5 中，我可以对 Y 进行条件化，条件是 X=1，本质上得到一个新的随机变量，它的取值与 Y 相同，但概率分布是 P(Y∣X=1)P(Y|X=1)P(Y∣X=1)。

对于有编程经验的读者，可以把条件化理解为对事件 X==1X == 1X==1 的过滤；例如，"当 X==1X == 1X==1 时，Y 的概率分布是什么？" 这种过滤类似于 SQL 查询中的 WHERE 子句。 P(Y)P(Y)P(Y) 是当你执行 SELECT * FROM Y 查询时 Y 表中所有行的分布，P(Y∣X=1)P(Y|X=1)P(Y∣X=1) 是当你执行 SELECT * FROM Y WHERE X=1 时 Y 表的分布。

将"条件化"理解为操作，有助于更好地理解概率机器学习库。在这些库中，随机变量用对象表示，而条件化是作用于这些对象的操作。你还会看到，将条件化视为操作与因果建模中"干预"（intervention）的核心概念形成对比，后者指的是"对随机变量进行干预"。

Pyro 库通过 pyro.condition 函数实现条件化操作。我们将在第3章详细探讨。

2.1.4 链式法则、全概率定律与贝叶斯定理

基于概率的基本公理，我们可以推导出链式法则、全概率定律和贝叶斯定理。这些概率定律在概率建模和因果建模中尤为重要，因此我们将简要介绍它们。

链式法则指出，联合概率可以分解为条件概率的乘积。例如，联合概率 <math xmlns="http://www.w3.org/1998/Math/MathML"> P ( X , Y , Z ) P(X,Y,Z) </math>P(X,Y,Z) 可以分解为：

我们可以按任意顺序进行分解。上面示例中是先分解 X，再分解 Y，最后分解 Z。然而，顺序为 Y、Z、X 或 Z、X、Y 等其他顺序同样是有效的。

链式法则在建模和计算方面都非常重要。实现一个表示 P(X,Y,Z)的单一对象的挑战在于，它需要将 X、Y 和 Z 所有可能结果的组合映射到对应的概率值。链式法则允许我们将 P(X,Y,Z)的因子分解为三个独立的任务，分别对应每个因子。

全概率定理则允许我们将边缘概率分布（单个变量的分布）与联合分布联系起来。例如，如果我们想从 X 和 Y 的联合分布 P(X, Y)中推导出 X 的边缘分布 P(X)，可以通过对 Y 求和来实现。

在图2.5中，我们通过对行中的Y求和来得到边缘分布 P(X)。当 XXX 是连续随机变量时，则对 Y行积分而非求和。

最后，我们有贝叶斯定理：

我们通过采用条件概率的原始定义，并对分子应用链式法则来推导出这个公式：

贝叶斯定理本身并不算特别有趣------它只是一个推导过程。更有意思的概念是贝叶斯主义，这是一种哲学思想，利用贝叶斯定理帮助建模者推理他们对所建模问题的主观不确定性。我将在第2.4节中涉及这一内容。

2.1.5 马尔可夫假设与马尔可夫核

在处理因素链的建模中，一个常见的方法是采用马尔可夫假设。该建模方法对变量的顺序作出简化假设，即序列中的每个元素只依赖于其前面的直接元素。例如，再次考虑如下的联合概率分解 P(x, y, z)：

如果我们应用马尔可夫假设，这将简化为：

这将允许我们用 <math xmlns="http://www.w3.org/1998/Math/MathML"> P ( z ∣ y ) P(z \mid y) </math>P(z∣y) 来代替 <math xmlns="http://www.w3.org/1998/Math/MathML"> P ( z ∣ x , y ) P(z \mid x, y) </math>P(z∣x,y)，这样更容易建模。在本书中，当我们遇到一个因子分解中经过马尔可夫假设简化的因子，比如 <math xmlns="http://www.w3.org/1998/Math/MathML"> P ( z ∣ y ) P(z \mid y) </math>P(z∣y)，我们称之为马尔可夫核（Markov kernel）。

马尔可夫假设是统计学和机器学习中一种常见的简化假设；实际上，在考虑了 Y 之后，Z 可能仍然依赖于 X，但我们假设这种依赖很弱，因此可以在模型中安全地忽略它。我们将在图形因果关系中看到，马尔可夫假设是关键------在给定直接原因的情况下，假设效果与间接原因相互独立。

2.1.6 参数

假设我想用代码实现概率分布的抽象表示，比如图 2.1 中的表格分布，以便于针对不同的有限离散结果进行建模。首先，如果我想建模另一个三面骰子，它的概率值可能不同，但我想保持图 2.8 中的基本结构。

在代码中，我可以将其表示为某种对象类型，该类型的构造函数接受两个参数，ρ1 和 ρ2，如图 2.9 所示（"ρ"是希腊字母"rho"）。

第三个概率值是其他两个概率值的函数（而不是第三个参数ρ3）的原因，是因为概率值必须加和为1。这两个值的集合{ρ1, ρ2}就是该分布的参数。从编程的角度来看，我可以创建一个数据类型来表示含有三个值的表格。当我想创建一个新的分布时，可以用这两个参数作为构造函数的参数，生成该类型的新实例。

最后，在三面骰子的例子中，有三个可能的结果{1, 2, 3}。如果我希望我的数据结构支持不同预先指定的结果数量，那么就需要一个参数来表示结果的数量。我们用希腊字母κ（Kappa，Κ）表示它。我的参数集为{Κ, ρ1, ρ2, ... ρΚ--1}，其中ρΚ是1减去其他所有ρ参数之和。

在pgmpy库的DiscreteFactor和TabularCPD类中，ρ（rho）表示传递给values参数的值列表，而Κ对应传递给cardinality、variable_card和evidence_card参数的值。一旦我们拥有了类似TabularCPD的概率分布表示，就可以用一组参数来指定该分布的实例。

希腊字母与罗马字母

在本书中，我用罗马字母（A、B、C）表示建模领域中的随机变量，比如"掷骰子"或"国内生产总值"，用希腊字母表示所谓的参数。这里的参数是指描述罗马字母变量概率分布的值。在统计学中，这种希腊字母与罗马字母的区分并不重要，比如贝叶斯统计学中，罗马字母和希腊字母都被视为随机变量。但在因果建模中，这种区分很关键，因为罗马字母可以表示因果关系的因果变量，而希腊字母则用来描述因果变量间的统计关系。

2.1.7 概率分布的典型类别

常见的概率分布类别有很多，比如我们刚刚学习的表格形式属于"分类分布"（categorical distributions）类别。分类分布表示离散结果的分布，这些结果可以看作是类别，如{"冰淇淋"，"冻酸奶"，"雪芭"}。伯努利分布是分类分布的特例，只含有两个可能结果。离散均匀分布是所有结果概率相等的分类分布。在实现时，分类分布可以直接定义在类别上（比如"正面"和"反面"），也可以定义在类别索引上（比如0和1）。

离散随机变量与连续随机变量

对于离散随机变量，我们用概率分布函数（probability distribution function，简称PDF）表示，记为P(X = x)，它返回变量取某一特定值的概率。对于连续随机变量，则有概率密度函数（probability density function），描述变量在某一区间内取值的相对可能性，通过对区间积分给出概率。

当具体情形中离散或连续的参数化很重要时，我们会特别指出，并用p(X = x)表示概率密度函数。但在本书中，我们主要关注因果问题的表述，不特别区分离散或连续变量。大多数情况下使用概率分布函数的表示P(X = x)，但请记住，因果思想同样适用于连续情形。

此外，还有适用于连续、有限或无限变量集的典型分布类别。例如，正态（高斯）分布类就描述了著名的"钟形曲线"。我用"类别"（或者更合适地说"类型"）这个词，是从计算机科学的角度出发，因为分布的具体实现要等到赋予希腊字母参数之后才算完成。对于正态（高斯）分布类别，其概率密度函数为：

这里，μ 和 σ 是参数。

图 2.10 是一个常见的图示，展示了几种常用的典型概率分布。图中分布之间的箭头表示它们之间的关系（例如，伯努利分布是二项分布的特例），这里我们不做深入探讨。

参数类型

在概率建模中，理解典型参数的含义非常有帮助。可以将分布中的概率视为一种稀缺资源，必须在所有可能的结果之间分配。某些结果可能分得更多，但总和必须等于或积分为1。参数描述了这有限的概率如何分配给各个结果。

打个比方，就像一个固定人口的城市。城市的参数决定了人口的分布。位置参数（如正态分布中的"μ"，μ是均值，但并非所有位置参数都是均值）就像你在谷歌地图中搜索城市名称时落下的那个定位针。这个针标记了一个精确点，我们称之为"市中心"。有些城市大部分人居住在市中心附近，离中心越远人口越少。但也有些城市，其他非中心区域人口密集。尺度参数（如正态分布中的"σ"，σ是标准差，但并非所有尺度参数都是标准差）决定人口的分布范围；洛杉矶的尺度参数就很大。形状参数（及其倒数，速率参数）影响分布的形状，既不像位置参数那样简单地平移，也不像尺度参数那样拉伸或压缩。举例来说，香港的形状偏斜，市区内有密集的摩天大楼，而九龙是更宽广的住宅区，建筑较矮且分布分散。

Pyro库提供了作为建模原语的典型分布。Pyro中对应离散分类分布表的是Categorical对象。

示例代码 2.3 Pyro中的典型参数

ini 复制代码 
import torch
from pyro.distributions import Bernoulli, Categorical, Gamma, Normal    #1

print(Categorical(probs=torch.tensor([.45, .30, .25])))    #2
print(Normal(loc=0.0, scale=1.0))
print(Bernoulli(probs=0.4))
print(Gamma(concentration=1.0, rate=2.0))

#1 Pyro包含了常用的典型分布。

#2 Categorical分布接受一个概率值列表，每个值对应一个结果。

这段代码输出如下分布对象表示：

scss 复制代码 
Categorical(probs: torch.Size([3]))
Normal(loc: 0.0, scale: 1.0)
Bernoulli(probs: 0.4000)
Gamma(concentration: 1.0, rate: 2.0)

log_prob方法不是返回概率值，而是返回概率值的自然对数，因为对数概率在计算上比普通概率更有优势。通过指数运算（取e的l次幂，l为对数概率）可转换回概率尺度。

例如，我们可以创建一个参数为0.4的伯努利分布对象：

ini 复制代码 
bern = Bernoulli(0.4)

该分布将值1.0的概率赋为0.4。出于数值计算原因，我们通常使用概率的自然对数。

我们可以用math库的exp函数将对数概率转换回概率尺度：

lua 复制代码 
lprob = bern.log_prob(torch.tensor(1.0))

import math
print(math.exp(lprob))

指数化对数概率返回的概率值如下：

复制代码 
0.3999999887335489

该值非常接近0.4，但由于计算机浮点数精度的舍入误差，略有不同。

使用典型分布的条件概率

常见的典型分布可用于描述单个随机变量（如随机向量或矩阵）。但我们可以利用链式法则将联合概率分布分解成条件概率分布，并用典型分布来表示。

例如，我们可以用下面的正态分布来表示条件于X和Z的Y分布，

其中位置参数 μ(x, z) 是 x 和 z 的函数。一个例子是下面的线性函数：

其他函数也同样可行，比如神经网络。这些 β 参数在机器学习中通常被称为权重参数。

2.1.8 分布的可视化

在概率建模和贝叶斯推断的场景中，我们常常通过视觉化来理解分布。对于离散变量，常见的可视化方式是条形图。例如，我们可以将图2.3中的概率以条形图的形式展示，如图2.11所示。需要注意的是，这不是直方图；我将在第2.3节中强调两者的区别。

当分布的取值集合是无限时，我们依然使用可视化方法。例如，图2.12展示了两个分布函数的叠加：一个离散的泊松分布和一个连续的正态（高斯）分布（我特意设定了两个分布，使它们有重叠部分）。泊松分布的取值没有上限（下限为0），但随着数值变大，概率逐渐减小，条形也越来越小，直到变得微小到无法绘制。正态分布则通过在图中绘制概率分布函数的曲线来可视化。正态分布没有上下界，但离中心越远，概率值越小。

条件概率分布的可视化涉及将每个条件变量映射到图像中的某个元素。例如，在图2.13中，X是离散变量，而Y在给定X的条件下服从正态分布，其中位置参数是X的函数。

由于 X 是离散变量，最简单的做法是将 X 映射为颜色，并叠加绘制条件概率曲线 P(Y | X=1)、P(Y | X=2) 和 P(Y | X=3)。但是，如果我们想要可视化 P(Y | X, Z)，则需要将 Z 映射到除颜色之外的美学元素，例如伪三维图中的第三个轴，或者图像网格中的行。但二维可视化能够承载的信息量有限。幸运的是，条件独立性帮助我们减少了条件变量的数量。

2.1.9 独立性和条件独立性

非正式来说，如果观察一个随机变量的结果不影响另一个随机变量结果的概率，即满足 P(y | x) = P(y)，则称两个随机变量独立，记作 X ⊥ Y。如果不独立，则称它们相关或依赖。

两个依赖变量在给定其他变量的条件下可以变为条件独立。例如，X ⊥ Y | Z 表示 X 和 Y 可能相关，但在给定 Z 的条件下它们是独立的。换句话说，如果 X 和 Y 依赖且满足 X ⊥ Y | Z，那么不再是 P(y | x) ≠ P(y)，而是 P(y | x, z) = P(y | z)。

独立性是简化模型的强大工具

独立性是简化概率分布表示的有力工具。设联合概率分布 P(W, X, Y, Z) 以表格形式表示，表格的单元格数等于 W、X、Y、Z 各自可能取值数的乘积。我们可以用链式法则将问题分解为因子 {P(W), P(X | W), P(Y | X, W), P(Z | Y, X, W)}，但这些因子参数的总数不变，总体复杂度相同。

若 X ⊥ W，则 P(X | W) 简化为 P(X)；若 Z ⊥ Y | X，则 P(Z | Y, X, W) 简化为 P(Z | X, W)。每次对联合概率分布施加一对条件独立约束，都能大幅降低模型复杂度。统计建模、机器学习中的正则化以及深度学习中的"drop-out"等技术，都在直接或间接地尝试对数据的联合概率分布施加条件独立。

条件独立与因果关系

条件独立是因果建模的基础。因果关系导致相关变量之间的条件独立。例如，孩子的血型由父母和祖父母的血型共同影响，这些血型彼此相关。但只需要知道父母的血型（直接原因），即可完全决定孩子的血型，如图2.14所示。用概率术语来说，孩子和祖父母的血型在给定父母血型条件下是条件独立的。

图 2.14 展示了因果关系如何导致条件独立。父母的血型决定了孩子的血型。祖父的血型与孩子的血型相关（虚线表示）。但父母的血型是直接原因，完全决定了孩子的血型。这些直接原因使得孩子和祖父的血型在条件上相互独立。

因果关系导致条件独立这一事实，使我们能够基于条件独立的证据来学习和验证因果模型。在第4章中，我们将以形式化的方式探讨条件独立与因果关系之间的联系。

2.1.10 期望值

随机变量函数的期望值是该函数所有可能输出值的加权平均数，其中权重是各结果发生的概率。

当可能的结果是连续的情况下，期望值通过积分来定义。

我们感兴趣的一些因果量度将以期望值来定义。这些量度只关注期望值本身，而不关心期望是如何计算的。在处理问题时，利用离散期望的基本算术直观要比连续情况下的积分运算更容易理解。因此，在本书中，当有选择时，我会采用离散随机变量和离散期望的例子。这些例子中的因果逻辑都可以推广到连续情况。

期望值具有许多有趣的数学性质。在本书中，我们关心的一个事实是条件期望在条件独立的情况下会简化：如果 <math xmlns="http://www.w3.org/1998/Math/MathML"> X ⊥ Y X \perp Y </math>X⊥Y，则 <math xmlns="http://www.w3.org/1998/Math/MathML"> E ( X ∣ Y ) = E ( X ) E(X \mid Y) = E(X) </math>E(X∣Y)=E(X)；如果 <math xmlns="http://www.w3.org/1998/Math/MathML"> X ⊥ Y ∣ Z X⊥Y∣Z </math>X⊥Y∣Z，则 <math xmlns="http://www.w3.org/1998/Math/MathML"> E ( X ∣ Y , Z ) = E ( X ∣ Z ) E(X∣Y,Z)=E(X∣Z) </math>E(X∣Y,Z)=E(X∣Z)。简单来说，如果两个变量 X 和 Y 独立，那么关于其中一个变量的期望不会因为知道另一个变量的信息而改变；如果这种独立性在给定第三个变量 Z 的条件下成立，那么在已知 Z 的情况下，对其中一个变量的期望不会因为另一个变量的信息而改变。

除此之外，期望值最重要的性质是线性，即期望可以通过线性函数。这里给出一些有用的期望线性性质的示例：

对于随机变量 X 和 Y，有：
<math xmlns="http://www.w3.org/1998/Math/MathML"> E ( X + Y ) = E ( X ) + E ( Y ) E(X + Y) = E(X) + E(Y) </math>E(X+Y)=E(X)+E(Y)

对于常数 a 和 b：
<math xmlns="http://www.w3.org/1998/Math/MathML"> E ( a X + b ) = a E ( X ) + b E(aX+b)=aE(X)+b </math>E(aX+b)=aE(X)+b

如果 X 只有两个取值 0 和 1，且 <math xmlns="http://www.w3.org/1998/Math/MathML"> E ( Y ∣ X ) = a X + b E(Y∣X)=aX+b </math>E(Y∣X)=aX+b，那么
<math xmlns="http://www.w3.org/1998/Math/MathML"> E ( Y ∣ X = 1 ) − E ( Y ∣ X = 0 ) = a E(Y∣X=1)−E(Y∣X=0)=a </math>E(Y∣X=1)−E(Y∣X=0)=a

（这是因为 <math xmlns="http://www.w3.org/1998/Math/MathML"> a × 1 + b − ( a × 0 + b ) = a a×1+b−(a×0+b)=a </math>a×1+b−(a×0+b)=a。提前透露一下：这点对基于线性回归的因果效应推断技术非常重要。）

随机变量分布的均值是该变量本身的期望值，即 <math xmlns="http://www.w3.org/1998/Math/MathML"> E ( X ) E(X) </math>E(X)（即函数是恒等函数， <math xmlns="http://www.w3.org/1998/Math/MathML"> f ( X ) = X ） f(X)=X） </math>f(X)=X）。在若干经典分布中，均值是参数的简单函数。例如，在正态分布中，位置参数等同于期望值。但位置参数和期望值并不总是相同的，比如柯西分布就有位置参数，但其均值是未定义的。

下一节，你将学习如何使用计算方法表示分布并计算期望值。

2.2 计算概率

为了在模型中使用概率，我们需要编写代码来表示概率分布和期望值。在上一节中，你已经看到了如何为一个三面骰子编码概率分布。但我们如何用代码来模拟掷一个三面骰子？如何编写代码表示两个条件独立的骰子掷骰结果？同时，我们如何让计算机执行计算期望值的数学运算？在计算机这个所有操作都是确定性的系统中，我们又如何让它掷骰子，使得结果在事先不可知？

2.2.1 概率的物理解释

假设我有一个三面骰子，每个面都有分配的概率值。这些概率值意味着什么？我们该如何解释它们？

假设我反复掷骰子，并统计每个结果出现的次数。掷骰是随机的，意思是尽管我每次以相同的方式掷骰，结果却不同。骰子的物理形状会影响统计结果；如果某一面比其他两面大，这个大小差异会影响出现次数。随着掷骰次数不断增多，某个结果出现的比例会趋近于某个数值。假设我把这个数值作为该结果的概率值，并解释为每次掷骰时出现该结果的"概率"。

这种观点称为物理概率（或频率学派概率）。物理概率指的是想象某个可重复的物理随机过程，产生一组可能结果中的某一个。概率值由该随机过程无限重复时，某结果出现比例的极限确定。我们将该概率解释为该物理过程产生该结果的倾向性。

2.2.2 随机生成

基于上述物理概率定义，我们可以定义随机生成。随机生成指的是算法从给定分布中随机选择一个结果。该算法的选择机制受物理概率启发；若无限次运行该算法，每个结果被选择的比例将趋近于该结果的概率值。

计算机是确定性机器。同样输入下，重复运行程序，输出总是相同的；它本身无法产生真正随机的结果（除非有随机输入）。计算机必须使用确定性算法来模拟随机生成，这些算法称为伪随机数生成器（pseudo-random number generators，PRNG）。它们以一个初始数字------随机种子（random seed）为起点，产生确定性的数列。数学上，这些算法保证生成的数列在统计意义上与理想的随机序列无异。

用符号表示，随机生成写作：

这句话的意思是："x 是从随机变量 X 的概率分布中生成的。"

在随机生成中，"generate"的同义词还有"simulate"（模拟）和"sample"（采样）。例如，在 pgmpy 库中，DiscreteFactor 类的 sample 方法就执行随机生成。它返回一个 pandas DataFrame。请注意，由于是随机生成，每次运行这段代码时，结果很可能不同：

清单2.4 在pgmpy中从DiscreteFactor模拟随机变量

ini 复制代码 
from pgmpy.factors.discrete import DiscreteFactor
dist = DiscreteFactor(
    variables=["X"],
    cardinality=[3],
    values=[.45, .30, .25],
    state_names= {'X': ['1', '2', '3']}
)

dist.sample(n=1)    #1
#1 n表示你希望生成的样本数量。

这将生成如图2.15所示的表格。

图2.15 从 P(X) 生成一个实例，会创建一个包含一行的 pandas DataFrame 对象。

我们也可以从联合概率分布中生成样本。

ini 复制代码 
joint = DiscreteFactor(
    variables=['X', 'Y'],
    cardinality=[3, 2],
    values=[.25, .20, .20, .10, .15, .10],
    state_names= {
        'X': ['1', '2', '3'],
        'Y': ['0', '1']
    }
)

joint.sample(n=1)

这会生成如图2.16所示的表格。

图2.16 从联合分布 P(X, Y) 生成一个实例，会创建一个包含一行的 pandas DataFrame 对象。

Pyro 也有用于典型分布的 sample 方法：

java 复制代码 
import torch
from pyro.distributions import Categorical

Categorical(probs=torch.tensor([.45, .30, .25])).sample()

这将从该分类分布中生成一个样本，即可能是 0、1 或 2。

tensor(1.)

2.2.3 编写随机过程的代码

当我们想以特定方式生成数值时，可以将随机过程写成代码。以代码形式写的随机过程有时称为随机函数（stochastic function）、概率子程序（probabilistic subroutine）或概率程序（probabilistic program）。例如，考虑联合概率分布 P(X, Y, Z)。我们如何从该联合分布中随机生成样本呢？遗憾的是，现有的软件库通常不支持任意联合分布的伪随机生成。

我们可以通过应用链式法则和（如果存在）条件独立性来解决这个问题。例如，我们可以将联合分布分解为：

假设在给定 X 的条件下，Y 与 Z 条件独立，那么：

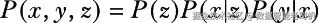
最后，假设我们可以从 P(Z)、P(X|Z) 和 P(Y|X) 这三个基本的随机生成函数中采样，那么我们就可以利用这个分解来构建一个采样算法：

这是一个可以在代码中执行的随机过程。首先，我们从 P(Z) 中生成一个 Z 的结果 z。然后以该 z 为条件生成 X 的结果 x。接着同样的方式生成 Y 的结果 y。最终，这个过程会从联合分布 P(X, Y, Z) 中生成一个元组 {x, y, z}。

在 pgmpy 中，我们可以使用名为 BayesianNetwork 的类来创建随机过程。

代码示例 2.5：在 pgmpy 和 Pyro 中创建随机过程

ini 复制代码 
from pgmpy.factors.discrete.CPD import TabularCPD
from pgmpy.models import BayesianNetwork
from pgmpy.sampling import BayesianModelSampling

PZ = TabularCPD(     #1
    variable='Z',     #1
    variable_card=2,  #1
    values=[[.65], [.35]],     #1
    state_names = {     #1
        'Z': ['0', '1']     #1
    }
)     #1

PXgivenZ = TabularCPD(     #2
    variable='X',    #2
    variable_card=2,   #2
    values=[   #2
        [.8, .6],   #2
        [.2, .4],   #2
    ],    #2
    evidence=['Z'],    #2
    evidence_card=[2],  #2
    state_names = {    #2
        'X': ['0', '1'],    #2
        'Z': ['0', '1']     #2
    }
)   #2

PYgivenX = TabularCPD(     #3
    variable='Y',     #3
    variable_card=3,     #3
    values=[    #3
        [.1, .8],     #3
        [.2, .1],     #3
        [.7, .1],    #3
    ],    #3
    evidence=['X'],     #3
    evidence_card=[2],    #3
    state_names = {    #3
        'Y': ['1', '2', '3'],    #3
        'X': ['0', '1']          #3
    }
)    #3

model = BayesianNetwork([('Z', 'X'), ('X', 'Y')])   #4
model.add_cpds(PZ, PXgivenZ, PYgivenX)     #5

generator = BayesianModelSampling(model)    #6
generator.forward_sample(size=1)    #7

注释说明：

  • #1 表示 P(Z)
  • #2 表示条件概率 P(X|Z=z)
  • #3 表示条件概率 P(Y|X=x)
  • #4 创建一个 BayesianNetwork 对象，参数为有向图中的边（本书第3章详细介绍）
  • #5 将条件概率分布添加到模型中
  • #6 从 BayesianNetwork 对象创建 BayesianModelSampling 对象
  • #7 从该对象中采样生成数据

运行该代码会生成一个 pandas DataFrame 中的一行数据，如图 2.17 所示。

图 2.17 展示了 forward_sample 方法如何模拟生成 X、Y 和 Z 的一个实例，以 pandas DataFrame 中的一行形式呈现。

实现用于随机生成的随机过程非常强大，因为它允许我们从那些无法用清晰的数学表达式或单一典型分布表示的联合分布中进行采样。例如，虽然 pgmpy 在处理分类分布方面表现良好，但 Pyro 提供了处理多种典型分布组合的灵活性。

下面的代码示例展示了前述随机过程的 Pyro 版本。它保留了 Z、X 和 Y 之间的依赖关系，但使用了不同的典型分布。

代码示例 2.6：在 Pyro 中处理典型分布组合

scss 复制代码 
import torch
from pyro.distributions import Bernoulli, Poisson, Gamma

z = Gamma(7.5, 1.0).sample()    #1
x = Poisson(z).sample()         #2
y = Bernoulli(x / (5 + x)).sample()   #3
print(z, x, y)
  • #1 用 Gamma 分布表示 P(Z) 并采样 z。
  • #2 用参数为 z 的 Poisson 分布表示 P(X|Z=z) 并采样 x。
  • #3 用 Bernoulli 分布表示 P(Y|X=x)，概率参数是 x 的函数。

示例输出类似：

scss 复制代码 
tensor(7.1545) tensor(5.) tensor(1.)

Z 服从 Gamma 分布，X 服从以 z 为均值参数的 Poisson 分布，Y 服从参数依赖于 x 的 Bernoulli 分布。

用编程语言实现随机函数，可以使用更细致的条件控制流程。考虑下面的伪代码：

ini 复制代码 
z ~ P(Z)
x ~ P(X|Z=z)
y = 0
for i in range(0, x):     #1
    y_i ~ P(Y|X=x)       #1
    y += y_i             #2
  • #1 这里使用了类似 for 循环的控制流来生成值。
  • #2 y 是循环中生成值的总和。y 仍然依赖于 x，但通过细致的控制流程体现。

此处 y 仍依赖于 x，但它定义为 x 个独立随机变量的和。在 Pyro 中，我们可以如下实现：

代码示例 2.7：带细致控制流程的随机过程示例（Pyro）

scss 复制代码 
import torch
from pyro.distributions import Bernoulli, Poisson, Gamma

z = Gamma(7.5, 1.0).sample()
x = Poisson(z).sample()
y = torch.tensor(0.0)    #1
for i in range(int(x)):   #1
    y += Bernoulli(.5).sample()   #1
print(z, x, y)
  • #1 y 被定义为随机抛硬币结果的总和，因此 y 从 P(Y|X=x) 生成，因为抛硬币次数依赖于 x。

在 Pyro 中，最佳实践是将随机过程实现为函数，并且使用 pyro.sample 函数生成样本，而不是直接调用分布对象的 sample 方法。我们可以将上面代码（示例 2.7）重写如下：

代码示例 2.8：使用函数实现随机过程并调用 pyro.sample

scss 复制代码 
import torch
import pyro

def random_process():
    z = pyro.sample("z", Gamma(7.5, 1.0))
    x = pyro.sample("x", Poisson(z))
    y = torch.tensor(0.0)
    for i in range(int(x)):
        y += pyro.sample(f"y{i}", Bernoulli(.5))    #1
    return y
  • #1 f"y{i}" 生成变量名如 "y0", "y1", 等。

pyro.sample 的第一个参数是字符串，用于为采样变量命名。当我们在第3章开始运行 Pyro 的推断算法时，这个命名机制的作用将会变得明显。

2.2.4 蒙特卡洛模拟与期望值

蒙特卡洛算法通过随机生成来估计感兴趣分布的期望值。其思路很简单：你有某种方法可以从 P(X)P(X)P(X) 中生成样本。如果你想计算 E(X)E(X)E(X)，就生成多个 xxx，然后取这些 xxx 的平均值。如果想计算 E(f(X))E(f(X))E(f(X))，则生成多个 xxx，对每个 xxx 应用函数 f(⋅)f(\cdot)f(⋅)，再取这些结果的平均值。蒙特卡洛方法即使在 XXX 是连续变量的情况下也同样适用。

在 pgmpy 中，你可以使用 sample 或 forward_sample 方法生成 pandas DataFrame，然后调用 pandas 的 mean 方法来计算平均值。

scss 复制代码 
generated_samples = generator.forward_sample(size=100)
generated_samples['Y'].apply(int).mean()

在 Pyro 中，我们通过反复调用 random_process 函数实现同样的功能。下面的代码使用一个循环生成 100 个样本：

scss 复制代码 
generated_samples = torch.stack([random_process() for _ in range(100)])

这段代码利用 Python 的列表推导式反复调用 random_process。注意 Pyro 是基于 PyTorch 的，它返回的 yyy 是一个张量。这里使用 torch.stack 将多个张量列表合并成一个张量，最后调用 mean 方法获得 E(Y)E(Y)E(Y) 的蒙特卡洛估计。

scss 复制代码 
generated_samples.mean()

我运行这段代码时得到的结果大约是 3.78，但你得到的结果可能略有不同。

你想了解的许多关于分布的内容都可以通过某个函数 f(X)来表达。例如，如果你想知道 <math xmlns="http://www.w3.org/1998/Math/MathML"> X > 10 X > 10 </math>X>10 的概率，可以生成一批 x，将大于 10 的 x转换成 1，其他转换成 0，然后取这些 1 和 0 的平均值，得到的值就是该概率的估计。

举例说明，下面的代码在之前的基础上计算 <math xmlns="http://www.w3.org/1998/Math/MathML"> E ( Y 2 ) E(Y^2) </math>E(Y2)：

scss 复制代码 
torch.square(generated_samples).mean()

在计算随机变量 X的期望 <math xmlns="http://www.w3.org/1998/Math/MathML"> E ( f ( X ) ) E(f(X)) </math>E(f(X)) 时，请记住先对样本应用函数，再取平均值以得到蒙特卡洛估计。如果你先对样本取平均，再应用函数，那么得到的是 <math xmlns="http://www.w3.org/1998/Math/MathML"> f ( E ( X ) ) f(E(X)) </math>f(E(X)) 的估计值，二者通常是不同的。

2.2.5 概率推断的编程实现

假设我们用代码实现了一个随机过程，从联合分布 <math xmlns="http://www.w3.org/1998/Math/MathML"> P ( X , Y , Z ) P(X, Y, Z) </math>P(X,Y,Z)中生成一个结果 <math xmlns="http://www.w3.org/1998/Math/MathML"> { x , y , z } \{x, y, z\} </math>{x,y,z}，过程如下：

进一步，假设我们想从条件分布 <math xmlns="http://www.w3.org/1998/Math/MathML"> P ( Z ∣ Y = 3 ) P(Z \mid Y=3) </math>P(Z∣Y=3) 中生成样本。我们该如何实现呢？我们的过程可以从 P(Z)、 <math xmlns="http://www.w3.org/1998/Math/MathML"> P ( X ∣ Z ) P(X \mid Z) </math>P(X∣Z) 和 <math xmlns="http://www.w3.org/1998/Math/MathML"> P ( Y ∣ Z ) P(Y \mid Z) </math>P(Y∣Z) 采样，但如何从这些分布推导出 <math xmlns="http://www.w3.org/1998/Math/MathML"> P ( Z ∣ Y ) P(Z \mid Y) </math>P(Z∣Y) 并不明确。

概率推断算法通常接受一个生成结果的随机过程和目标分布作为输入，输出一个从目标分布生成样本的方法。这类算法通常称为贝叶斯推断算法，因为它们常用贝叶斯定理将 <math xmlns="http://www.w3.org/1998/Math/MathML"> P ( Y ∣ Z ) P(Y \mid Z) </math>P(Y∣Z) 转换为 <math xmlns="http://www.w3.org/1998/Math/MathML"> P ( Z ∣ Y ) P(Z \mid Y) </math>P(Z∣Y)。不过，这种关联并不总是显式的，所以我更倾向称其为"概率推断"而非"贝叶斯推断算法"。

例如，一类简单的概率推断算法称为接受/拒绝算法。利用简单的接受/拒绝方法生成 <math xmlns="http://www.w3.org/1998/Math/MathML"> P ( Z ∣ Y = 3 ) P(Z \mid Y=3) </math>P(Z∣Y=3) 的步骤如下：

  1. 使用我们的生成器反复生成 <math xmlns="http://www.w3.org/1998/Math/MathML"> { x , y , z } \{x, y, z\} </math>{x,y,z}。
  2. 丢弃所有 <math xmlns="http://www.w3.org/1998/Math/MathML"> y ≠ 3 y \neq 3 </math>y=3 的生成样本。
  3. 剩下的 ZZZ 的样本集即符合 <math xmlns="http://www.w3.org/1998/Math/MathML"> P ( Z ∣ Y = 3 ) P(Z \mid Y=3) </math>P(Z∣Y=3)的分布。

用 Pyro 举例，我们将之前的 random_process 函数改写为返回 z 和 y，然后对 <math xmlns="http://www.w3.org/1998/Math/MathML"> E ( Z ∣ Y = 3 ) E(Z \mid Y=3) </math>E(Z∣Y=3)进行蒙特卡洛估计。

scss 复制代码 
import torch
import pyro
from pyro.distributions import Bernoulli, Gamma, Poisson

def random_process():
    z = pyro.sample("z", Gamma(7.5, 1.0))
    x = pyro.sample("x", Poisson(z))
    y = torch.tensor(0.0)
    for i in range(int(x)):
        y += pyro.sample(f"{i}", Bernoulli(.5))
    return z, y    # 新版本返回 z 和 y

generated_samples = [random_process() for _ in range(1000)]  # 生成1000个样本
z_mean = torch.stack([z for z, _ in generated_samples]).mean()  # 计算 E(Z)
print(z_mean)

这段代码估计 E(Z)。由于 Z 是从 Gamma 分布模拟而来，其真实均值是形状参数 7.5 除以速率参数 1.0，即 7.5。

接下来，我们对 <math xmlns="http://www.w3.org/1998/Math/MathML"> E ( Z ∣ Y = 3 ) E(Z \mid Y=3) </math>E(Z∣Y=3)进行估计，只保留Y=3的样本：

scss 复制代码 
z_given_y = torch.stack([z for z, y in generated_samples if y == 3])
print(z_given_y.mean())

运行该代码的一次结果是 tensor(6.9088)，结果会有轻微差异。该推断算法在 <math xmlns="http://www.w3.org/1998/Math/MathML"> Y = 3 Y=3 </math>Y=3 频繁出现时表现良好。如果该事件较罕见，则算法效率低下，需要生成大量样本以满足条件，浪费许多样本。

概率推断还有许多其他算法，但主题较为广泛且与因果建模关联较弱，此处不做深入探讨。更多资料和相关示例代码，请访问 www.altdeep.ai/p/causalaib...。

概率加权方法

这类方法先从联合分布中生成样本，再根据目标分布的概率加权这些样本，通过蒙特卡洛加权平均完成估计。重要采样和逆概率加权是常见变体，后者在因果推断中广泛应用，本书第11章将介绍。

概率图模型的推断

概率图模型通过图结构表达联合分布中的条件独立性，支持基于图的推断算法，如变量消元和信念传播。变量消元即通过对概率表中某变量求和"消去"该变量，实现对目标分布的求解。信念传播通过消息传递在图中邻接的"团"间传递信息，迭代更新参数直至收敛，最终得到目标变量的分布。

图形推断的优势之一是无需用户手动实现，诸如 pgmpy 等软件自动完成。理论上有一些限制，但在实际应用中通常无碍。本书重点介绍因果图模型，这是一种特殊的概率图模型，适合因果推断，并可利用图形推断方法解决因果问题。

变分推断

变分推断通过编写一个生成近似分布样本的新随机过程，并利用深度学习中常用的梯度优化技术调优其参数，尽量使近似分布贴近目标分布。Pyro 视变分推断为主要推断方式，将生成近似分布样本的过程称为"引导函数（guide function）"，高级 Pyro 用户善于设计此类函数。Pyro 还支持"自动引导函数生成"，是推断"商品化"的另一表现。

马尔可夫链蒙特卡洛（MCMC）

MCMC 是计算贝叶斯学派广泛使用的推断算法，属于接受/拒绝类。每次新生成的样本依赖于前一个未被拒绝的样本，形成一条样本链，链中样本的分布最终收敛到目标分布。Hamiltonian Monte Carlo（HMC）是流行版本，无需用户自行实现生成器。Pyro 和 PyMC 等库均实现了 HMC 和其他 MCMC 算法。

高级推断方法

生成模型研究不断涌现新推断技术，如对抗推断、归一化流推断和扩散模型推断，目标是高效采样机器学习中常见的复杂分布。更多资料请参见 www.altdeep.ai/p/causalaib...。本书第6章将展示利用归一化流的结构因果模型。总体上，本书采用第一章提到的推断"商品化"趋势，以便构建并利用现有及未来发布的新推断算法的因果模型。

2.3 数据、总体、统计量与模型

到目前为止，我们讨论了随机变量和分布。现在，我们将转向数据和统计量。首先定义一些术语。你对"数据"可能已有直观认识，但这里我们结合本章已有内容给出定义：数据是一组随机变量或随机变量集合的记录结果。统计量是从数据计算出来的任何量。例如，当你用训练数据训练神经网络时，学到的权重参数值就是统计量，模型的预测结果也是统计量（因为它们通过权重依赖于训练数据）。

产生特定数据流的现实世界因果过程称为数据生成过程（Data Generating Process, DGP）。模型是该过程的简化数学描述。统计模型则是在参数经过调优后，使模型与数据中的统计模式相匹配的模型。

本节介绍理解本书所需的数据与统计相关核心概念。

2.3.1 以概率分布作为总体的模型

在应用统计学中，我们从数据中提取统计洞察，并推广到总体。例如，考虑第1章提到的MNIST手写数字分类问题。假设训练分类模型的目的是将其部署到用于数字化书面文本的软件中。那么总体就是软件将来可能见到的所有文本中的所有数字。

总体是异质的，意味着总体中的个体存在差异。网站上的某个功能可能整体提升用户参与度，但对于某些子群体，该功能可能反而降低参与度，因此需要针对合适的子群体进行定向。市场营销中称之为"细分"。

再举一例，一种药物对大多数患者可能无显著效果，但对某些子群体却有效。精准医疗领域正是以此为目标，针对特定子群体施治。

在概率模型中，我们用概率分布来建模总体。利用条件概率建模子群体尤其有用。例如，设 <math xmlns="http://www.w3.org/1998/Math/MathML"> P ( E ∣ F = True ) P(E \mid F = \text{True}) </math>P(E∣F=True) 表示接触某网站功能的所有用户的参与度分布，则 <math xmlns="http://www.w3.org/1998/Math/MathML"> P ( E ∣ F = True , G = "millennial" ) P(E \mid F = \text{True}, G = \text{"millennial"}) </math>P(E∣F=True,G="millennial")表示接触该功能且属于"千禧一代"子群体的用户参与度分布。

总体的模型：典型分布与随机过程

既然用概率分布建模总体，那么针对不同总体应选择哪些典型分布呢？图2.18展示了常见分布及其通常用于描述的现象。

这些选择并非凭空而来。典型分布本身是由随机过程导出的。例如，二项分布是通过进行一系列抛硬币试验得到的结果。当某个现象是许多独立（或弱依赖）微小变化的累积结果时，会得到正态分布。等待时间分布描述了等待某事件发生所需的时间分布（例如，设备故障或交通事故）。当已等待时间的长短不影响剩余等待时间时，指数分布适用于这种等待时间（例如放射性原子衰变所需的时间）。如果事件发生的时间服从指数分布，那么在固定时间段内事件发生的次数则服从泊松分布。

概率建模中的一个实用技巧是，思考生成目标总体的随机过程。然后根据该过程选择合适的典型分布，或在代码中实现该随机过程，利用各种典型分布作为代码逻辑中的基本构件。在本书中，我们将看到这种思路与因果建模高度契合。

抽样、独立同分布（IID）与生成

通常，我们拥有的数据并不是整个总体，而是总体的一个小样本。随机选择个体的行为称为抽样。当数据是通过不断从总体中抽样获得时，得到的数据集称为随机样本。如果我们能将数据视为随机样本，就称该数据为独立同分布（IID）。这意味着每个数据点的抽取方式相同且相互独立，且所有数据都来源于相同的总体分布。图2.19展示了如何从总体中选择IID随机样本。

抽样和独立同分布（IID）数据的概念体现了使用概率分布来建模总体的第二个优势。我们可以通过从该分布生成数据来模拟从总体中抽样。具体来说，可以先编写一个表示总体的随机过程，再将其与一个从总体过程中生成数据的过程结合起来，从而模拟IID抽样。

在pgmpy中，这个操作非常简单，只需生成多个样本即可：

ini 复制代码 
generator.forward_sample(size=10)

这会生成如图2.20所示的数据表。

Pyro中用于独立同分布（IID）采样的方法是 pyro.plate。

示例代码 2.10：在Pyro中生成IID样本

scss 复制代码 
import pyro
from pyro.distributions import Bernoulli, Poisson, Gamma

def model():
    z = pyro.sample("z", Gamma(7.5, 1.0))
    x = pyro.sample("x", Poisson(z))
    with pyro.plate("IID", 10):     #1
        y = pyro.sample("y", Bernoulli(x / (5+x)))    #2
    return y

model()

#1 pyro.plate 是一个上下文管理器，用于生成条件独立的样本。这里会生成10个IID样本。

#2 调用 pyro.sample 会生成一个结果 y，它是一个包含10个IID样本的张量。

使用生成过程来模拟抽样在机器学习中特别有用，因为数据往往不是IID。例如，第1章提到的MNIST数据，原始NIST数据并非IID------一部分数据来自高中生，另一部分来自政府官员。你可以将数字书写者的身份作为随机过程中的一个变量，那么在这个变量条件下数据就是IID的。

不要把地图当成地形

再来看MNIST数据。这个数据的总体是非常模糊和抽象的。如果该数字分类软件授权给多个客户，那么总体将是几乎无尽的数字流。在机器学习和统计学中，推广到抽象总体是常见场景。现代统计学奠基人R.A. Fisher在设计作物生长土壤类型实验时，也试图以尽可能少的样本去推广到未来作物总体。

处理模糊庞大总体时，容易犯的错误是把总体和概率分布混淆。千万不要把"地图"（用于建模总体的分布）当作"地形"（总体本身）。

举个例子：写这章内容时，我正在葡萄牙阿尔加维的Silves度假，那里有座大城堡、悠久历史和优美徒步路径。假设我想建模Silves居民的身高。

官方统计显示Silves人口为11,000，因此我们以此作为真实总体大小。这意味着Silves有11,000个不同的身高值。假如我亲自去国家卫生中心，拿到了一份每个居民身高的电子表格。此时，我的数据不是总体的随机样本，而是完整的总体数据。

随后我可以计算该总体的直方图，如图2.21所示。直方图是对总体或样本中数值（这里是身高）计数的可视化。对于连续值，如身高，我们统计落入某一区间（或称"箱"）的数值数量。

这个直方图代表了完整的人口分布。我可以通过将计数除以总人数，使其更像一个概率分布，如图2.22所示。

有人可能会说这个分布符合正态（高斯）概率分布，因为我们看到的是钟形曲线，实际上正态分布适用于进化中呈钟形的现象，比如身高。但这句话并不完全准确。原因是，所有的正态分布都是定义在包括负数的范围内的（尽管负数部分的概率密度可能极小），而身高是不可能为负的。我们实际上是在将正态分布作为一个模型------作为对该人口分布的近似。

另一个例子是，图2.23展示了简·奥斯汀小说中词性（parts of speech）的真实分布。注意，这并不是基于她小说中部分页面的样本，而是根据她六部已完成小说中共计72.5万个词的词性分布制作的可视化图表。

作为建模者，我们使用典型分布（canonical distributions）来建模总体分布，但模型并不等同于总体分布。这个观点看似语义学上的细节，但在大数据时代，我们往往能够对整个总体进行推理，而不仅仅是随机样本。例如，流行的在线社交网络拥有数亿甚至数十亿用户，这样庞大的规模，整个总体数据几乎只需一次数据库查询即可获取。

在因果建模中，准确理解如何看待数据与总体的建模非常重要。因果推断关注的是总体的真实属性，而不仅仅是数据中的统计趋势。不同的因果问题需要我们将不同的因果假设融入模型，其中有些假设较强且较难验证。

2.3.2 从观测数据到数据生成过程（DGP）

在因果建模中，理解观测数据如何映射回数据中的变量的联合概率分布，以及该联合概率分布如何映射回数据生成过程（DGP）非常关键。大多数建模者对这些实体间的关系都有一定直觉，但因果建模需要我们明确表达。这种明确的理解很重要，因为在普通统计建模中，我们建模的是联合分布（或其部分），而因果建模中需要建模的是数据生成过程（DGP）。

从观测数据到经验联合分布

假设我们有表2.1所示的包含五个数据点的数据集。

表2.1 简单数据集示例

序号 jenny_throws_rock brian_throws_rock window_breaks
1 False True False
2 True False True
3 False False False
4 False False False
5 True True True

我们可以对所有观测到的可观察结果进行计数，结果见表2.2。

表2.2 各种可能结果组合的经验计数

序号 jenny_throws_rock brian_throws_rock window_breaks counts
1 False False False 2
2 True False False 0
3 False True False 1
4 True True False 0
5 False False True 0
6 True False True 1
7 False True True 0
8 True True True 1

将计数除以总样本数5，即可得到经验联合分布，如表2.3所示。

表2.3 数据的经验分布

序号 jenny_throws_rock brian_throws_rock window_breaks proportion
1 False False False 0.40
2 True False False 0.00
3 False True False 0.20
4 True True False 0.00
5 False False True 0.00
6 True False True 0.20
7 False True True 0.00
8 True True True 0.20

因此，对于离散型结果，我们通过计数从数据转化为经验分布。

对于连续型结果，我们可以计算直方图、密度曲线或其他统计表示形式。这些都是对同一潜在经验分布的不同表现。

值得注意的是，经验联合分布并非数据中变量的真实联合分布。例如，我们看到经验分布中有些结果在这五个数据点中未出现。它们的出现概率是否为零？更可能的是这些概率大于零，但因为样本太少，我们没观察到这些结果。

举个比喻，公平的骰子掷出1的概率是1/6。如果你掷5次骰子，有约40%的概率（即 (1--1/6)^5）完全没出现1。如果发生了，你不会因此断定掷出1的概率是零。若继续掷骰子，掷出1的频率会渐近于1/6。

注：更精确地说，频率主义概率解释告诉我们，概率是无限重复掷骰时掷出1的比例。虽然是"无限次"，但通常不需要掷太多次比例就开始收敛。

从经验联合分布到观测联合分布

观测联合概率分布是数据中变量的真实联合分布。假设表2.4显示了这些观测变量的真实联合分布。

表2.4 假设的真实观测联合分布

序号 jenny_throws_rock brian_throws_rock window_breaks probability
1 False False False 0.25
2 True False False 0.15
3 False True False 0.15
4 True True False 0.05
5 False False True 0.00
6 True False True 0.10
7 False True True 0.10
8 True True True 0.20

从观测联合分布采样，会产生经验联合分布，如图2.24所示。

潜变量：从观测联合分布到完整联合分布

在统计建模中，潜变量是指那些在数据中未被直接观测到但被包含在统计模型中的变量。回到我们之前的数据示例，假设存在第四个潜变量"strength_of_impact"（冲击强度），其数值如表2.5所示。

表2.5 strength_of_impact列中的数值是未观测到的"潜变量"

序号 jenny_throws_rock brian_throws_rock strength_of_impact window_breaks
1 False True 0.6 False
2 True False 0.6 True
3 False False 0.0 False
4 False False 0.0 False
5 True True 0.8 True

潜变量模型在机器学习、计量经济学、生物信息学等多个学科中非常常见。例如，在自然语言处理领域，一个流行的概率潜变量模型是主题模型，其中观测变量表示文档中词语和短语的出现情况，而潜变量则代表文档的主题（如体育、政治、金融等）。

由于潜变量未被直接观测，它们被省略在观测联合概率分布之外。包含观测变量和潜变量的联合概率分布被称为完整联合分布。要从完整联合分布得到观测联合分布，需要对潜变量进行边际化处理，如图2.25所示。

从完整联合分布到数据生成过程（DGP）

我用以下 Python 代码编写了五个数据点的实际数据生成过程（DGP）示例。

ini 复制代码 
def true_dgp(jenny_inclination, brian_inclination, window_strength):     #1
    jenny_throws_rock = jenny_inclination > 0.5     #2
    brian_throws_rock = brian_inclination > 0.5    #2
    if jenny_throws_rock and brian_throws_rock:    #3
        strength_of_impact = 0.8   #3
    elif jenny_throws_rock or brian_throws_rock:     #4
        strength_of_impact = 0.6    #4
    else:     #5
        strength_of_impact = 0.0   #5
    window_breaks = window_strength < strength_of_impact    #6
    return jenny_throws_rock, brian_throws_rock, window_breaks

注释说明：

  1. 输入变量反映了 Jenny 和 Brian 扔石头的倾向，以及窗户的强度。
  2. 如果有倾向，Jenny 和 Brian 就会扔石头。
  3. 如果两人都扔石头，撞击总强度为0.8。
  4. 如果只有其中一人扔石头，撞击强度为0.6。
  5. 否则没人扔石头，撞击强度为0。
  6. 如果撞击强度大于窗户强度，窗户破碎。

注意：一般来说，数据生成过程是未知的，我们的模型只能对其结构进行猜测。

在这个示例中，jenny_inclination、brian_inclination 和 window_strength 是介于0到1之间的潜变量。jenny_inclination 表示 Jenny 最初的扔石头意愿，brian_inclination 表示 Brian 的扔石头意愿，window_strength 表示窗户玻璃的强度。这些是导致观测变量（jenny_throws_rock、brian_throws_rock、window_breaks）产生的一组初始条件。

然后，我用以下五组潜变量调用了 true_dgp 函数：

ini 复制代码 
initials = [
    (0.6, 0.31, 0.83),
    (0.48, 0.53, 0.33),
    (0.66, 0.63, 0.75),
    (0.65, 0.66, 0.8),
    (0.48, 0.16, 0.27)
]

换句话说，下面这个 Python 循环就是生成这五个数据点的采样过程：

css 复制代码 
data_points = []
for jenny_inclination, brian_inclination, window_strength in initials:    
    data_points.append(
        true_dgp(
            jenny_inclination, brian_inclination, window_strength
        )
    )

数据生成过程（DGP）即是生成数据的因果过程。请注意，完整联合概率分布中完全缺失了叙事元素：Jenny 和 Brian 如果有扔石头的意愿，就会扔石头；如果石头击中了窗户，窗户可能会破碎，这取决于两人是否都扔了石头以及窗户的强度。DGP 包含完整联合概率分布，正如图2.26所示。换言之，联合概率分布是基于 DGP 如何生成数据的结果。

总结来说，数据生成过程（DGP）包含完整的联合分布，对完整联合分布进行边缘化得到观测联合分布。从该分布采样会生成观测数据及相应的经验联合分布。在这个层级结构中，存在多对一的关系，这对因果建模和推断具有重要影响。

层级结构中的多对一关系

随着我们从数据生成过程（DGP）向完整联合分布，再到观测联合分布，继而到经验联合分布和观测数据逐层推进，前一层级到后一层级之间存在多对一的关系，如图2.27所示。

同样，某一层级的一个对象可以对应上一层级的多个对象：

  • 可能存在多个观测联合分布与同一个经验联合分布一致。如果我们先采样五个点，再采样另外五个点，就会得到不同的数据集，从而产生不同的经验分布。
  • 可能存在多个完整联合分布与同一个观测联合分布一致。它们之间的差异在于潜变量。但如果我们对潜变量的集合有不同选择呢？例如，如果我们的观测分布是 P(X, Y)，当潜变量集合是 {Z, W} 时，完整联合分布是 P(X, Y, Z, W)；当潜变量集合是 {Z, V} 时，完整联合分布是 P(X, Y, Z, V)。
  • 可能存在多个数据生成过程（DGP）与同一个完整联合分布一致。假设在我们砸窗户的例子中，Jenny 有个朋友 Isabelle，有时会鼓动 Jenny 扔石头，有时不会，这影响了 Jenny 的倾向。这种 DGP 与原始的不同，但 Isabelle 的同伴压力与 Jenny 的倾向之间的潜变量关系可能使得该新 DGP 导出了完全相同的联合概率分布。更简单的例子是，考虑三个骰子点数和的分布。DGP 是掷三个骰子并求和。两个 DGP 可能只在求和顺序不同，例如 (第一个 + 第二个) + 第三个，或者 (第一个 + 第三个) + 第二个，或者 (第二个 + 第三个) + 第一个，但它们都会产生相同的分布。

后面两个多对一关系是因果可识别性的基础概念，这也是因果推断之所以困难的核心原因。正如那句俗语所说，"相关不代表因果"。

2.3.3 独立性的统计检验

因果关系对变量施加独立性和条件独立性的限制，因此我们依赖条件独立性的统计检验来构建和验证因果模型。

假设 X 和 Y 是独立的，或者在给定 Z 的条件下，X 和 Y 是条件独立的。如果我们有观测到的 X、Y 和 Z 数据，就可以进行独立性统计检验。标准的统计独立性检验会给出一个检验统计量，用以量化 X 和 Y 之间的统计关联程度，同时给出一个 p 值，表示在 X 和 Y 实际条件独立于 Z 的情况下，纯粹偶然地观察到该统计关联程度或更极端的概率。简单来说，这种检验衡量的是依赖或独立的统计证据。

指控某人犯下谋杀罪的证据不等同于确定其真凶。同样，统计上显示两个变量独立的证据，也不等于它们真正独立。两种情况下，证据都只能指向一个结论，但无法绝对证明它。比如，即便独立性成立，统计证据的强度也会受到数据量等多个因素影响，而且这些检验始终可能导致错误结论。

请记住，如果 X 和 Y 独立，那么 P(Y|X) = P(Y)。在预测层面，这意味着 X 对 Y 没有预测能力。如果不能使用经典统计检验（例如 X 和 Y 是向量时），可以尝试训练预测模型并主观评估模型的预测效果。

2.3.4 模型参数的统计估计

当我们"训练"或"拟合"一个模型时，实际上是在尝试估计模型参数的值，比如回归模型或神经网络中的权重参数。通常，在统计建模和机器学习中，参数估计的目标是对观测的联合概率分布进行建模；而在因果建模中，目标是对数据生成过程（DGP）进行建模。这个区别对于做出正确的因果推断非常重要。

通过最大化似然估计

非正式地讲，似然表示在给定参数向量的候选值时观察到数据的概率。最大化似然就是选择使得似然值最大的参数向量。通常，我们最大化的是似然的对数（对数似然），因为数学和计算上更简便；最大化似然和最大化对数似然得到的结果是一样的。在某些特殊情况（如线性回归）下，最大似然估计有明确的数学解，但一般情况下需要用数值优化方法求解。对于某些模型（如神经网络），找到最大似然的参数值不可行，因此我们只能找到似然较高的候选参数。

通过最小化其他损失函数和正则化估计

在机器学习中，有多种损失函数用来估计参数。最大化似然其实是最小化某种损失函数的特例，即负对数似然损失函数。

正则化是在损失函数中加入额外项，引导优化过程得到更优参数。例如，L2正则化会在损失中加入与参数值平方和成比例的项。由于参数值的微小增加会导致平方值的大幅增加，L2正则化有助于避免参数估计过大。

贝叶斯估计

贝叶斯估计将参数视为随机变量，试图建模在观测数据条件下参数的条件分布（通常称为后验分布）。它通过给参数设定一个"先验概率分布"来实现。先验分布本身由模型者指定的"超参数"决定。当模型中存在潜变量时，贝叶斯推断的目标是参数和潜变量在观测数据条件下的联合分布。

如前所述，本书中用希腊字母表示参数，用罗马字母表示数据生成过程中的变量（包括潜变量）。但对于贝叶斯统计学家来说，这种区分并不重要，因为参数和潜变量都是未知的，都是推断的对象。

贝叶斯估计的主要优势之一是，它不仅给出参数的点估计，而是提供参数的完整条件概率分布（或者说是代表该分布的样本或参数值）。这种概率分布体现了对参数值的不确定性，并且可以将这种不确定性纳入模型预测或其他推断中。

根据贝叶斯哲学，先验分布应体现模型者对参数真实值的主观信念。我们在因果建模中也会类似地，将对因果结构和DGP机制的信念转化为模型中的因果假设。

估计量的统计和计算属性

既然存在多种估计参数的方法，我们需要比较这些方法的优劣。假设我们要估计的参数有真实值，统计学家关心估计方法恢复真实值的能力，特别关注偏差和一致性。估计量是一个随机变量，因为它来源于数据（而数据有分布），因此估计量本身也有分布。若估计量分布的均值等于被估计参数的真实值，则称该估计量无偏。一致性意味着数据量越大，估计值越接近真实值。实际上，一致性比无偏性更重要。

计算机科学家则更关心估计方法在面对大数据时的计算性能：估计方法是否能随数据规模扩展？是否支持并行计算？估计量即使是一致的，但在手机应用上运行时，能否在毫秒级内收敛且不耗电？

本书将因果逻辑与估计因果参数的统计和计算性质分开讲解，重点关注因果逻辑，并依赖如 DoWhy 这类库来简化统计和计算工作。

拟合优度与交叉验证

参数估计后，我们可以计算各种统计量来评估估计效果。其中一类称为拟合优度统计量，用以量化模型对训练数据的拟合程度。换句话说，拟合优度统计告诉你模型在多大程度上"假装"是数据的DGP。然而，正如前面所讲，同一数据集可能对应多种DGP，拟合优度并不能提供辨别真实DGP的因果信息。

交叉验证统计量一般反映模型对未见数据的预测能力。有些模型相较于其他模型拟合优度不错，但预测效果仍差。机器学习通常关注预测任务，因此更看重交叉验证。然而，一个预测性能好的模型不一定能给出正确的因果推断。

2.4 确定性与主观概率

本节将探讨我们进行概率因果建模时所需的哲学基础。在本书中，我们将使用概率模型来构建因果模型。在训练模型时，我们可能会用到贝叶斯参数估计方法；在做因果推断时，可能会用概率推断算法；在因果决策时，则可能采用贝叶斯决策理论。此外，结构因果模型（第6章）对模型中随机性的产生位置有严格要求。因此，清楚区分贝叶斯主义、不确定性、随机性、概率建模与概率推断之间的关系十分重要。

第一个关键点是将数据生成过程（DGP）视为确定性的。第二个关键点是将我们对DGP模型中的概率视为主观概率。

2.4.1 确定性

之前关于扔石头的DGP代码是完全确定性的；给定初始条件，输出是确定的。再回顾一下我们对物理概率的定义：为什么掷骰子的结果是随机的？

假如我有超人的灵巧、感知和思维计算能力，我就能在脑海中计算骰子掷出的物理过程，从而完全确定结果。这个哲学观点称为确定论，它基本上认为DGP是确定性的。18世纪法国学者皮埃尔-西蒙·拉普拉斯提出了一个思想实验"拉普拉斯妖"，设想存在一个实体（妖），它知道宇宙中每个原子的精确位置和动量。凭借这些知识，它可以通过牛顿力学定律计算出宇宙的未来状态，确定无疑。换句话说，给定所有原因，结果是100%确定的，完全不存在随机性。

当然，某些系统在足够细致的观察下具有内在的随机性（如量子力学、生物化学等）。但这种哲学模型视角适用于我们大多数关心的建模对象。

2.4.2 主观概率

在我们物理概率的解释中，当我掷骰子时，概率表示我缺乏"拉普拉斯妖"那种对所有骰子粒子位置和动量的超人级知识。换句话说，当我构建DGP的概率模型时，概率反映的是我的无知。这种哲学思想称为主观概率或贝叶斯概率。它的观点超越了贝叶斯规则和贝叶斯统计估计，认为模型中的概率代表模型者对DGP缺乏完全知识，而非DGP本身的固有随机性。

主观概率扩展了我们"随机物理过程"的概率解释。物理概率解释适用于像掷骰子、抛硬币、洗牌这类简单的物理重复过程。但当然，我们也想建模许多难以视为可重复物理过程的现象。例如，思想如何转化为语言，或气候变化导致海洋淡水流量增加进而威胁全球洋流系统的稳定。在这些情况下，我们仍用随机生成来建模。随机生成中用到的概率反映了作为模型者的我们，虽然了解DGP的部分细节，但永远不可能拥有超人般的确定性细节。

总结

  • 随机变量是一个变量，其可能取值是随机现象的数值结果。
  • 概率分布函数将随机变量的结果映射为概率值。联合概率分布函数将X和Y的每种结果组合映射为概率值。
  • 我们从概率的基本公理推导出链式法则、全概率定律和贝叶斯定理，这些都是建模中的重要规则。
  • 马尔可夫假设指变量序列中每个变量仅依赖于其前一个变量，是统计建模中常用的简化假设，在因果建模中作用显著。
  • 典型分布类是数学上良好描述的分布类型，为概率建模提供灵活且易用的基本构件。
  • 典型分布通过一组参数实例化，如位置、尺度、速率和形状参数。
  • 在建模时，了解变量之间的独立性或条件独立性可极大简化模型；在因果建模中，这对区分相关性与因果性至关重要。
  • 离散随机变量的期望值是所有可能结果的加权平均，权重为各结果的概率。
  • 概率仅是一个数值，需要赋予其意义。物理概率定义将概率解释为若物理过程无限重复，某结果出现的比例。
  • 与物理概率不同，贝叶斯主观概率将概率解释为对事件的信念或不确定性的表达。
  • 编写随机过程时，Pyro允许使用典型分布作为构建细腻随机模型的原语。
  • 蒙特卡洛算法利用随机生成估计感兴趣分布的期望值。
  • 流行的推断算法包括基于图模型的算法、概率加权法、马尔可夫链蒙特卡洛（MCMC）和变分推断。
  • 典型分布和随机过程可作为我们希望建模和推断的人群的代理，条件概率则是建模异质子群的优秀方法。
  • 不同的典型分布用于描述不同现象，如计数、钟形曲线和等待时间。
  • 从随机过程中生成数据是对独立同分布（IID）样本现实采样的良好模拟。
  • 给定数据集，可能存在多个数据生成过程（DGP）产生该数据，这揭示了因果关系与相关关系解析的难点。
  • 统计独立性检验用于验证关于基础分布的独立性和条件独立性的假设。
  • 参数学习方法多样，包括最大似然估计和贝叶斯估计。
  • 确定性认为若我们知晓系统全部信息，可零误差预测结果；主观概率认为概率反映模型者对系统知识的不足。采纳这些哲学视角有助于理解因果AI。
  • 一种良好建模方法是对联合分布因子分解，利用条件独立简化因子，再将因子实现为随机过程。
  • 概率分布用于建模人群是一种强有力的技术，尤其关注人群异质性时。
  • 通过概率分布建模人群时，可以将从随机过程生成样本对应于从人群抽样。
  • 传统统计建模侧重于观测联合分布或完整联合分布，而因果建模关注的是数据生成过程（DGP）。
相关推荐
要努力啊啊啊27 分钟前
GQA（Grouped Query Attention）：分组注意力机制的原理与实践《一》
论文阅读·人工智能·深度学习·语言模型·自然语言处理
原味奶茶_三分甜1 小时前
Qwen3高效微调
深度学习
嘻嘻哈哈OK啦4 小时前
day40打卡
人工智能·深度学习·机器学习
yzx9910137 小时前
Python开发系统项目
人工智能·python·深度学习·django
my_q9 小时前
机器学习与深度学习08-随机森林02
深度学习·随机森林·机器学习
不爱吃山楂罐头10 小时前
第三十三天打卡复习
python·深度学习
m0_6786933310 小时前
深度学习笔记25-RNN心脏病预测(Pytorch)
笔记·rnn·深度学习
蹦蹦跳跳真可爱58911 小时前
Python----目标检测（《SSD: Single Shot MultiBox Detector》论文和SSD的原理与网络结构）
人工智能·python·深度学习·神经网络·目标检测·计算机视觉
LeonDL16812 小时前
HALCON 深度学习训练 3D 图像的几种方式优缺点
人工智能·python·深度学习·3d·halcon·halcon训练3d图像·深度学习训练3d图像
只有左边一个小酒窝13 小时前
（三）动手学线性神经网络：从数学原理到代码实现
人工智能·深度学习·神经网络
热门推荐
01机器学习实验--- 金融数据基础与计算在线实验闯关02KGG转MP3工具|非KGM文件|解密音频03YOLOv8入门 | 重要性能衡量指标、训练结果评价及分析及影响mAP的因素【发论文关注的指标】04从零安装 LLaMA-Factory 微调 Qwen 大模型成功及所有的坑05【SpeedAI科研小助手】2分钟极速解决知网维普重复率、AIGC率过高，一键全文降！文件格式不变，公式都保留的！06DeepSeek各版本说明与优缺点分析07【解决】Android Gradle Sync 报错 Could not read workspace metadata08【2025年最新】OpenWrt 更换国内源的指南（图形界面版)09组基轨迹建模 GBTM的介绍与实现（Stata 或 R）10山东大学2024深度学习期末考试回忆