C++_红黑树

本篇文章是对C++学习的红黑树部分的学习分享

希望也能够为你带来些许帮助~

那咱们废话不多说，直接开始吧！

---

一、红黑树基础概念

1. 红黑树的定义

• 本质：自平衡二叉搜索树，通过颜色标记同时确保没有⼀条路径会⽐其他路 径⻓出2倍实现近似平衡。
• 核心：每个节点增加颜色属性（红色 / 黑色），通过 4 条规则约束路径长度。

2. 红黑树的核心规则

1. 每个节点非红即黑。
2. 根节点为黑色。
3. 红色节点的子节点必为黑色（无连续红节点）。
4. 从任意节点到其所有叶子节点的路径中，黑色节点数量相同。

• 补充说明：部分资料将空节点（NIL）视为黑色叶子节点，实际实现中可忽略 NIL，通过规则间接保证平衡。

3. 平衡原理：为何最长路径不超过最短路径的 2 倍？

• 最短路径 ：全黑节点路径，长度为黑高（bh）。
• 最长路径 ：红黑交替路径，长度为 2*bh（规则 3 限制连续红色）。

但上述两种情况都是属于十分极端的情况，理论上最短路径与最长路径并不是在每一棵红黑树上都存在的。因此任意一条从根到NULL结点路径的⻓度为 X 便满足这个关系：bh<= X<=2*bh

二、红黑树的实现

1. 红黑树的结构

enum Color
{
	RED,
    BLACK
};

template<class K,class V>
struct RBTreeNode
{
	pair<K, V> _kv;
	RBTreeNode<K, V>* _left;
	RBTreeNode<K, V>* _right;
	RBTreeNode<K, V>* _parent;
	Color _col;

	RBTreeNode(const pair<K,V> kv)
		:_kv(kv)
		,_left(nullptr)
		,_right(nullptr)
		,_parent(nullptr)
		,_col(RED)
	{}
};

template<class K,class V>
class RBTree
{
	typedef RBTreeNode<K, V> Node;
public:

//...

private:
	Node* _root = nullptr;
};

2. 插入操作

2.1 插入流程概述

1. 按二叉搜索树规则插入新节点，默认颜色为红色（避免破坏规则 4）。
2. 处理颜色冲突 ：若父节点为红色，违反规则 3，需根据叔叔节点（uncle）的状态分情况调整。

2.2 不同情况处理方式

情况 1：叔叔节点存在且为红色（变色处理）

• 条件 ：当前节点（c）为红色，父节点（p）为红色，祖父节点（g）为黑色，叔叔节点（u）存在且为红色。
• 操作 ：
  • 将 p 和 u 染黑，g 染红。
  • 以 g 为新当前节点，继续向上检查平衡。
• 特点：仅变色，不旋转，需递归向上调整。

（三角形都为下层省略的二叉树结构）

情况 2：叔叔节点不存在或为黑色（旋转 + 变色）

子情况 2.1：单旋（左左或右右结构）

• 左左结构 ：p 是 g 的左子节点，c 是 p 的左子节点 → 以 g 为轴右单旋，p 染黑，g 染红。
• 右右结构 ：p 是 g 的右子节点，c 是 p 的右子节点 → 以 g 为轴左单旋，p 染黑，g 染红。

以左左结构为例（右右结构类似）

子情况 2.2：双旋（左右或右左结构）

• 左右结构 ：p 是 g 的左子节点，c 是 p 的右子节点 → 先左旋 p，再右旋 g，c 染黑，g 染红。
• 右左结构 ：p 是 g 的右子节点，c 是 p 的左子节点 → 先右旋 p，再左旋 g，c 染黑，g 染红。

以左右结构为例（右左结构类似）

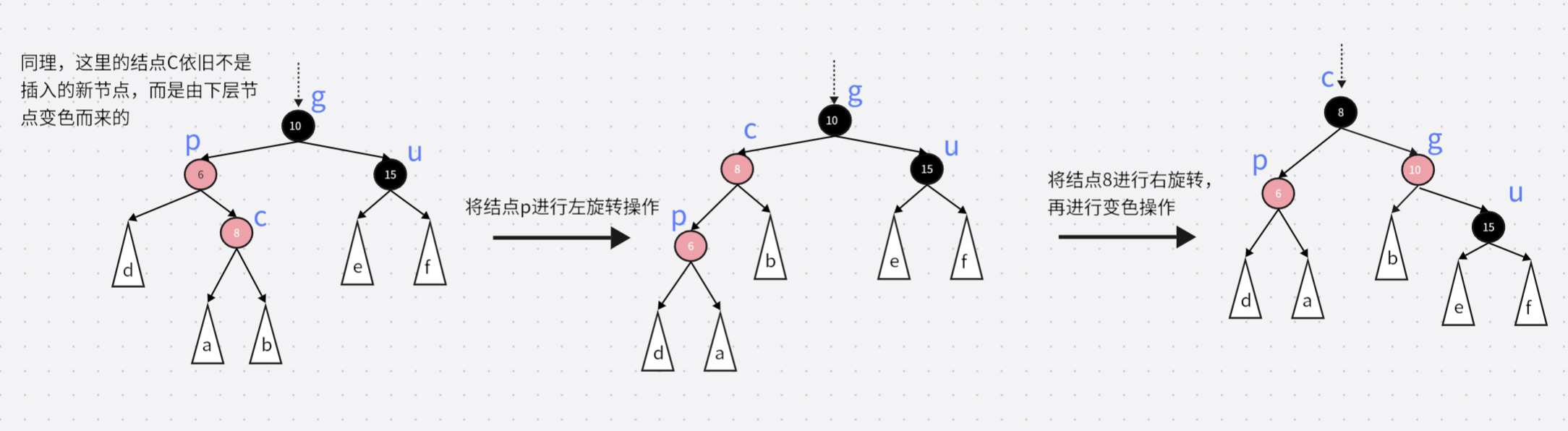
2.3 插入操作代码实现

bool insert(pair<K, V> kv)
{
	//根节点存在判断，没有就创建一个黑色根节点
	if (_root == nullptr)
	{
		_root = new Node(kv);
		_root->_col = BLACK;
		return true;
	}

	Node* cur = _root;
	Node* parent = nullptr;

	while (cur)
	{
		parent = cur;
		if (cur->_kv.first < kv.first)
		{
			cur = cur->_right;
		}
		else if (cur->_kv.first > kv.first)
		{
			cur = cur->_left;
		}
		else
		{
			return false;
		}
	}

	cur = new Node(kv);
	cur->_parent = parent;//设置父指针

	if (parent->_kv.first > cur->_kv.first)
	{
		parent->_left = cur;
	}
	else
	{
		parent->_right = cur;
	}


	while (parent && parent->_col == RED)
	{
		Node* grandparent = parent->_parent;
		if (!grandparent)//安全检查
			break;

		if (parent == grandparent->_left)
		{
			Node* uncle = grandparent->_right;
			//uncle存在且颜色为红
			if (uncle && uncle->_col == RED)
			{
				parent->_col = BLACK;
				uncle->_col = BLACK;
				grandparent->_col = RED;

				//再往上处理
				cur = grandparent;
				parent = cur->_parent;
			}

			//uncle不存在或uncle存在且颜色为黑
			else
			{
				if (cur == parent->_right)
				{
					RotateL(parent);
					// 旋转后parent和cur位置变化
					swap(parent, cur);
				}
				// 情况3: cur是parent的左孩子
				RotateR(grandparent);
				parent->_col = BLACK;
				grandparent->_col = RED;
				break;
			}
		}
		else
		{
			Node* uncle = grandparent->_left;
			//uncle存在且颜色为红
			if (uncle && uncle->_col == RED)
			{
				parent->_col = BLACK;
				uncle->_col = BLACK;
				grandparent->_col = RED;

				cur = grandparent;
				parent = cur->_parent;
			}

			//uncle不存在或uncle存在且颜色为黑
			else
			{
				if (cur == parent->_left)
				{
					RotateR(parent);
					// 旋转后parent和cur位置变化
					swap(parent, cur);
				}
				RotateL(grandparent);
				parent->_col = BLACK;
				grandparent->_col = RED;
				break;

			}
		}
		
	}
	_root->_col = BLACK;
	return true;
}

3. 查找操作

按⼆叉搜索树逻辑实现即可，搜索效率为 O(logN)

bool find(const pair<K,V> kv)
{
	Node* cur = _root;
	while (cur)
	{
		if (cur->_kv.first < kv.first)
		{
			cur = cur->_right;
		}
		else if (cur->_kv.first > kv.first)
		{
			cur = cur->_left;
		}
		else
		{
			return true;
		}
	}
	return false;
}

4. 红黑树"合法"判断

规则 1：颜色枚举保证非黑即红，无需显式检查。

规则 2：根节点必为黑色。

规则 3：前序遍历检查，禁止红色节点的父节点为红色。

规则 4：计算所有路径的黑色节点数是否一致。

bool IsBalanceTree()
{
	if (_root == nullptr)
	{
		return true;
	}
	
	Node* cur = _root;
	int refNum = 0;
	while (cur) 
	{
		if (cur->_col == BLACK)
		{
			refNum++;
		}
		cur = cur->_left;
	}
	return Check(_root, 0, refNum);
}

bool Check(Node* root,int blackNum,int refNum)
{
	if (root == nullptr)
	{
		if (blackNum != refNum)
		{
			cout << "存在诶色戒点不相等的路径" << endl;
			return false;
		}
		return true;
	}
	
	if (root->_col == RED && root->_parent && root->_parent->_col == RED)
	{
		cout << root->_kv.first << "存在连续的红色结点" << endl;
		return false;
	}
	if (root->_col == BLACK)
	{
		blackNum++;
	}
	return (Check(root->_left, blackNum, refNum) 
		&& Check(root->_right, blackNum, refNum));
}

---

那么本次关于红黑的知识分享就此结束了

非常感谢你能够看到这里

如果感觉对你有些许的帮助也请给我三连 这会给予我莫大的鼓舞！

之后依旧会继续更新C++学习分享

那么就让我们

下次再见~