三维重建 —— 1. 摄像机几何

文章目录

• [1. 针孔相机](#1. 针孔相机)
• • [1.1. 针孔成像](#1.1. 针孔成像)
  • [1.2. 光圈对成像的影响](#1.2. 光圈对成像的影响)
• [2. 透视投影相机](#2. 透视投影相机)
• • [2.1. 透镜成像](#2.1. 透镜成像)
  • [2.2. 失焦](#2.2. 失焦)
  • [2.3. 径向畸变](#2.3. 径向畸变)
  • [2.4. 透视投影的性质](#2.4. 透视投影的性质)
• [3. 世界坐标系到像素坐标系的变换](#3. 世界坐标系到像素坐标系的变换)
• [4. 其它相机模型](#4. 其它相机模型)
• • [4.1. 弱透视投影摄像机](#4.1. 弱透视投影摄像机)
  • [4.2. 正交投影摄像机](#4.2. 正交投影摄像机)
  • [4.3. 各种摄像机模型的应用场合](#4.3. 各种摄像机模型的应用场合)

课程视频链接： 计算机视觉之三维重建（深入浅出SfM与SLAM核心算法）------1.摄像机几何。

1. 针孔相机

1.1. 针孔成像

若将胶片直接置于物体前方成像，胶片上单个感光点会接收来自物体不同位置的光线，导致成像模糊。

在物体与胶片之间设置带针孔的隔板，限制光线仅通过小孔进入。这种结构确保了胶片上每一点仅接收来自物体上对应点的光线，显著提升了成像清晰度。

由此引出针孔相机模型，如下图所示：

在成像平面上，物体成像是倒立的。为便于观察和分析，可通过引入虚拟像平面，使成像物体呈现正立状态。

在针孔相机模型中，依据相似三角形原理，相机坐标系下的三维点 P ( x , y , z ) P(x, y, z) P(x,y,z) 与其在图像坐标系中的二维投影点 P ′ ( x ′ , y ′ ) P'(x', y') P′(x′,y′) 满足以下投影关系：
{ x ′ = f ⋅ x z y ′ = f ⋅ y z (1) \begin{cases} x' = f \cdot \dfrac{x}{z} \\ \\ y' = f \cdot \dfrac{y}{z} \tag{1} \end{cases} ⎩ ⎨ ⎧x′=f⋅zxy′=f⋅zy(1)其中， f f f 为相机焦距。

1.2. 光圈对成像的影响

从上图中我们可以看出，随着针孔尺寸减小（光圈缩小），图像清晰度逐渐提升，但亮度相应降低。当光圈为 2mm 时，虽然图像亮度较高，但因胶片上单点接收了物体多个区域的光线，呈现出模糊状态；而光圈缩小时，通过光线量减少降低了亮度，但光线近似单点传播的特性使得图像清晰度显著提升。

如果要提升图像亮度，需增大光圈孔径（即扩大针孔尺寸），但这会导致成像模糊------因为更大光圈允许多方向光线同时进入，使成像点扩散形成弥散斑。为了实现亮度与清晰度的同步优化，需要引入透镜。透镜通过折射原理将物体各点发出的光线会聚到胶片对应位置，在增加进光量的同时维持点对点成像的清晰度。

2. 透视投影相机

2.1. 透镜成像

加入透镜后，物体表面任意一点发出的多条散射光线，经透镜折射后可汇聚于胶片平面的对应点，显著提升该成像点的光强度，从而增强整体图像的亮度和清晰度。

透视成像的两大光学特性：

• 所有与光轴平行的入射光线，经透镜折射后必定会聚于焦点，该焦点到透镜光心的垂直距离定义为焦距 f f f
• 穿过透镜光心的任意光线（无论是否平行于光轴），其传播方向不发生偏折

透镜焦距 f f f 的计算公式如下：
f = R 2 ( n − 1 ) f = \dfrac{R}{2(n - 1)} f=2(n−1)R其中， R R R 为透镜球面半径， n n n 为透镜折射系数。

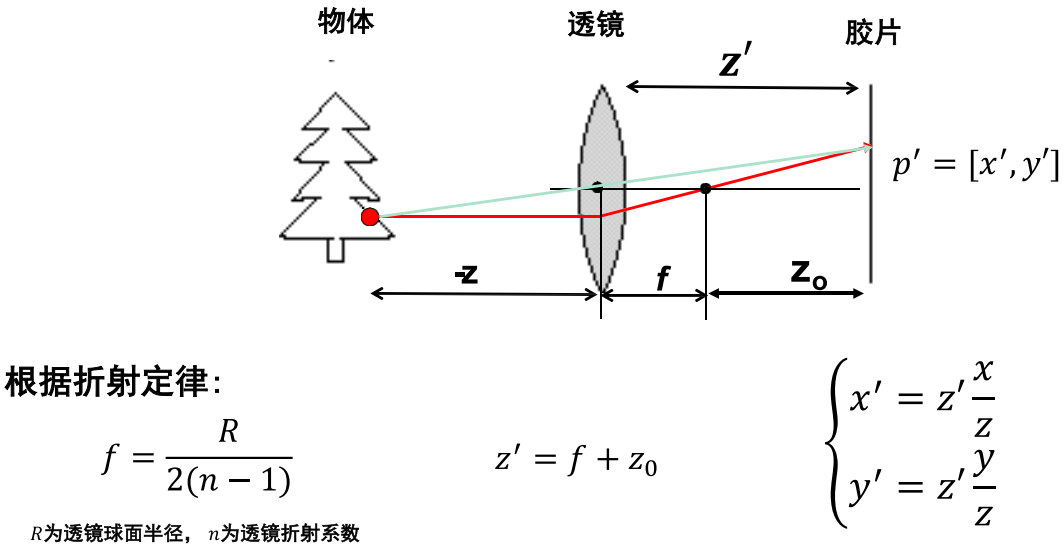
加入透镜后，相机坐标系点 P P P 到图像坐标系点 P ′ P' P′ 的变换关系仍可基于针孔模型建立，这是由光线穿过透镜光心不发生偏折的特性决定的（如图穿过透镜光心的光线路径）。我们需要将针孔相机模型中的 f f f 替换为 f + z 0 f + z_0 f+z0（其中 f f f 为透镜的焦距），公式如下：
{ x ′ = z ′ x z = ( f + z 0 ) x z y ′ = z ′ y z = ( f + z 0 ) y z \begin{cases} x' = z' \dfrac{x}{z} = (f + z_0) \dfrac{x}{z} \\ \\ y' = z' \dfrac{y}{z} = (f + z_0) \dfrac{y}{z} \end{cases} ⎩ ⎨ ⎧x′=z′zx=(f+z0)zxy′=z′zy=(f+z0)zy

2.2. 失焦

根据透镜成像公式：
1 u + 1 v = 1 f (3) \dfrac{1}{u} + \dfrac{1}{v} = \dfrac{1}{f} \tag{3} u1+v1=f1(3)其中：

• u u u 是物距，表示物体到透镜光心的距离
• v v v 是像距，表示像到透镜光心的距离
• f f f 是透镜的焦距

由于透镜的焦距 f f f 是常数，当我们知道物距 u u u 时，可以根据公式 ( 3 ) (3) (3) 计算出像距，如下图所示：

​为了清晰地拍摄物体，我们通常需要进行对焦：通过调整像距，使物距 u u u 和像距 v v v 满足公式 1 u + 1 v = 1 f \dfrac{1}{u} + \dfrac{1}{v} = \dfrac{1}{f} u1+v1=f1​，从而使被摄物体在成像平面上清晰成像。如下图所示，我们调整像距 v v v，使得位于 ​物面 1​ 的点能在成像平面上清晰成像。而位于该物面前后的 ​物面 2​ 和 ​物面 3​ 上的点则无法清晰成像，它们将在成像平面上呈现为弥散圆。

弥散圆是指焦点外的光线会在成像面上形成模糊的圆形光斑（弥散圆）。若其直径小于人眼可分辨的极限（容许弥散圆），则视为"清晰"。

根据以上的分析，引出景深的概念，当相机对焦于某一点时，该点前后一定距离内的物体也能清晰成像，这一清晰范围即为景深。焦点前的清晰范围叫前景深，焦点后的清晰范围叫后景深，两者之和为总景深。

值得注意的是：针孔相机是不存在景深的。传统镜头相机通过透镜聚焦光线，形成焦点平面，焦点前后的物体会因失焦产生模糊（弥散圆），从而形成有限的景深范围。而针孔相机仅通过微小孔径（针孔）成像，光线以直线传播，不依赖透镜聚焦，因此所有距离的物体均能保持相对清晰，不存在焦点前后的模糊区域。

景深范围外的物体在像平面上的成像会形成较大的弥散圆，导致视觉效果模糊，如下图所示：

2.3. 径向畸变

理想镜头应使所有光线（无论是否通过光轴）均聚焦于同一点。但对于实际镜头，远离光轴的光线（远轴光线）在通过镜头边缘时，折射角度可能超过理想值，导致成像点沿径向（即从图像中心向外的方向）偏移，从而产生径向畸变。

径向畸变分为枕形畸变和桶形畸变，其中：

• 桶形畸变（负畸变）：边缘光线折射角度偏小，使图像边缘向外拉伸，形如木桶（如广角镜头常见）
• 枕形畸变（正畸变）：边缘光线折射角度偏大，使图像边缘向内收缩，形如枕头（如长焦镜头常见）

径向畸变可通过以下数学模型进行校正：
{ x distorted = x ( 1 + k 1 r 2 + k 2 r 4 + k 3 r 6 ) y distorted = y ( 1 + k 1 r 2 + k 2 r 4 + k 3 r 6 ) \begin{cases} x_{\text{distorted}} = x(1 + k_1 r^2 + k_2 r^4 + k_3 r^6) \\ \\ y_{\text{distorted}} = y(1 + k_1 r^2 + k_2 r^4 + k_3 r^6) \end{cases} ⎩ ⎨ ⎧xdistorted=x(1+k1r2+k2r4+k3r6)ydistorted=y(1+k1r2+k2r4+k3r6)其中：

• ( x distorted , y distorted ) (x_{\text{distorted}} , y_{\text{distorted}}) (xdistorted,ydistorted) 为畸变后的像素坐标
• ( x , y ) (x, y) (x,y) 为畸变前的像素坐标
• r = x 2 + y 2 r = \sqrt{x^2 + y ^2} r=x2+y2 为像素点到图像原点的距离
• k 1 , k 2 , k 3 k_1, k_2, k_3 k1,k2,k3 为径向畸变系数

2.4. 透视投影的性质

3. 世界坐标系到像素坐标系的变换

参考博客：世界坐标系到像素坐标系的变换，可得：
z c ( u v 1 ) = ( 1 d x − c o t θ d x c x 0 1 s i n θ 1 d y c y 0 0 1 ) ( f 0 0 0 0 f 0 0 0 0 1 0 ) ( R T 0 1 ) ( x w y w z w 1 ) = ( f x − f x cot ⁡ θ c x 0 0 f y 1 sin ⁡ θ c y 0 0 0 1 0 ) ( R T 0 1 ) ( x w y w z w 1 ) = K [ I , 0 ] ( R T 0 1 ) ( x w y w z w 1 ) = K [ R , T ] ( x w y w z w 1 ) = M P w \begin{align*} z_c \begin{pmatrix} u \\ v \\ 1 \end{pmatrix} &= \begin{pmatrix} \dfrac{1}{dx} & -\dfrac{cot\theta}{dx} & c_x \\ 0 & \dfrac{1}{sin\theta} \dfrac{1}{dy} & c_y \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} f & 0 & 0 & 0 \\ 0 & f & 0 & 0 \\ 0 & 0 & 1 & 0 \end{pmatrix} \begin{pmatrix} R & T \\ 0 & 1 \end{pmatrix} \begin{pmatrix} x_w \\ y_w \\ z_w \\ 1 \end{pmatrix} \\ &= \begin{pmatrix} f_x & -f_x \cot \theta & c_x & 0 \\ 0 & f_y\dfrac{1}{\sin \theta} & c_y & 0 \\ 0 & 0 & 1 & 0 \end{pmatrix} \begin{pmatrix} R & T \\ 0 & 1 \end{pmatrix} \begin{pmatrix} x_w \\ y_w \\ z_w \\ 1 \end{pmatrix} \\ &= K [I, 0] \begin{pmatrix} R & T \\ 0 & 1 \end{pmatrix}\begin{pmatrix} x_w \\ y_w \\ z_w \\ 1 \end{pmatrix} = K [R, T] \begin{pmatrix} x_w \\ y_w \\ z_w \\ 1 \end{pmatrix} = M P_w \end{align*} zc uv1 = dx100−dxcotθsinθ1dy10cxcy1 f000f0001000 (R0T1) xwywzw1 = fx00−fxcotθfysinθ10cxcy1000 (R0T1) xwywzw1 =K[I,0](R0T1) xwywzw1 =K[R,T] xwywzw1 =MPw课程中给出的变换公式如下：

课程中公式的 α \alpha α 和 β \beta β 相当于博客中的 f x f_x fx 和 f y f_y fy， P ′ P' P′ 相当于 ( u z v z z ) \begin{pmatrix} uz \\ vz \\ z\end{pmatrix} uzvzz ，这是因为齐次坐标 ( u z v z z ) \begin{pmatrix} uz \\ vz \\ z\end{pmatrix} uzvzz 和 ( u v 1 ) \begin{pmatrix} u \\ v \\ 1\end{pmatrix} uv1 表示的是同一个像素点。

设 M = ( m 1 m 2 m 3 ) M = \begin{pmatrix} m_1 \\ m_2 \\ m_3\end{pmatrix} M= m1m2m3 ，我们可以对上述坐标转换公式做进一步简化有：
P ′ = M P w = ( m 1 m 2 m 3 ) P w = ( m 1 P w m 2 P w m 3 P w ) → ( m 1 P w m 3 P 3 m 2 P w m 3 P 3 ) P' = MP_w = \begin{pmatrix} m_1 \\ m_2 \\ m_3\end{pmatrix} P_w = \begin{pmatrix} m_1 P_w \\ m_2 P_w \\ m_3 P_w\end{pmatrix} \rightarrow \begin{pmatrix} \dfrac{m_1 P_w}{m_3 P_3} \\ \\ \dfrac{m_2 P_w}{m_3 P_3}\end{pmatrix} P′=MPw= m1m2m3 Pw= m1Pwm2Pwm3Pw → m3P3m1Pwm3P3m2Pw

4. 其它相机模型

4.1. 弱透视投影摄像机

弱透视投影摄像机是计算机视觉和三维重建中一种简化的摄像机模型，用于在特定条件下近似复杂的透视投影。它基于一个关键假设：物体距离摄像机足够远，使得物体上各点的深度变化可以忽略不计。

已知物体与摄像机之间的距离 z 0 z_0 z0 远大于物体本身的尺寸（例如，拍摄远处的建筑物或者人体），则将物体上各点的深度 z z z 近似等于 z 0 z_0 z0，即 z ≈ z 0 z ≈ z_0 z≈z0。

设 M = ( A b v 1 ) = ( m 1 m 2 m 3 ) M = \begin{pmatrix} A & b \\ v & 1 \\ \end{pmatrix} = \begin{pmatrix} m_1 \\ m_2 \\ m_3\end{pmatrix} M=(Avb1)= m1m2m3 ，则有 P ′ = ( m 1 P w m 2 P w m 3 P w ) = ( u z v z z ) P' = \begin{pmatrix} m_1 P_w \\ m_2 P_w \\ m_3 P_w\end{pmatrix} = \begin{pmatrix} uz \\ vz \\ z\end{pmatrix} P′= m1Pwm2Pwm3Pw = uzvzz ，则有
{ m 1 P w = u z m 2 P w = v z m 3 P w = z \begin{cases} m_1 P_w = uz \\ m_2 P_w = vz \\ m_3 P_w = z \end{cases} ⎩ ⎨ ⎧m1Pw=uzm2Pw=vzm3Pw=z在弱透视投影摄像机中，物体上所有点满足 z = z 0 z = z_0 z=z0，假设 m 3 = ( a , b , c , d ) m_3 = (a, b, c, d) m3=(a,b,c,d)，则 m 3 P w = ( a , b , c , d ) ⋅ ( x w y w z w 1 ) = a x w + b y w + c z w + d = z 0 m_3P_w = (a, b, c, d) \cdot \begin{pmatrix} x_w \\ y_w \\ z_w \\ 1\end{pmatrix} = ax_w + by_w + cz_w + d = z_0 m3Pw=(a,b,c,d)⋅ xwywzw1 =axw+byw+czw+d=z0，所以有：
{ a = 0 b = 0 c = 0 d = z 0 \begin{cases} a = 0 \\ b = 0 \\ c = 0 \\ d = z_0 \end{cases} ⎩ ⎨ ⎧a=0b=0c=0d=z0即 m 3 = ( 0 , 0 , 0 , z 0 ) m_3 = (0, 0, 0, z_0) m3=(0,0,0,z0)。

不妨令 { m ~ 1 = m 1 Z 0 m ~ 2 = m 2 Z 0 m ~ 3 = m 3 Z 0 = [ 0 , 0 , 0 , 1 ] \begin{cases} \tilde{m}_1 = \dfrac{m_1}{Z_0} \\ \\ \tilde{m}_2 = \dfrac{m_2}{Z_0} \\ \\ \tilde{m}_3 = \dfrac{m_3}{Z_0}=[0, 0, 0, 1] \end{cases} ⎩ ⎨ ⎧m~1=Z0m1m~2=Z0m2m~3=Z0m3=[0,0,0,1]则有：
M = ( m ~ 1 m ~ 2 m ~ 3 ) = ( m ~ 1 m ~ 2 [ 0 , 0 , 0 , 1 ] ) = ( A b 0 1 ) M = \begin{pmatrix} \tilde{m}_1 \\ \tilde{m}_2 \\ \tilde{m}_3\end{pmatrix} = \begin{pmatrix} \tilde{m}_1 \\ \tilde{m}_2 \\ [0, 0,0,1] \end{pmatrix} = \begin{pmatrix} A & b \\ 0 & 1 \end{pmatrix} M= m~1m~2m~3 = m~1m~2[0,0,0,1] =(A0b1)这和课程中的表达式一致：

4.2. 正交投影摄像机

4.3. 各种摄像机模型的应用场合